数据结构：栈与队列的核心概念与模拟实现

带鱼吃猫2026-01-28 8:18

目录

一、什么是栈

[1.1 栈的实现](#1.1 栈的实现)

[1.2 栈的应用（非递归快排）](#1.2 栈的应用（非递归快排）)

二、什么是队列

[2.1 队列的实现](#2.1 队列的实现)

[2.2 队列的应用（环形队列的生产消费模型）](#2.2 队列的应用（环形队列的生产消费模型）)

三、总结一下

一、什么是栈

在数据结构中，栈（Stack） 是一种遵循 后进先出（Last In First Out，简称 LIFO） 原则的线性数据结构，它只允许在一端进行数据的插入和删除操作，这个操作端被称为栈顶，而另一端则被称为栈底。

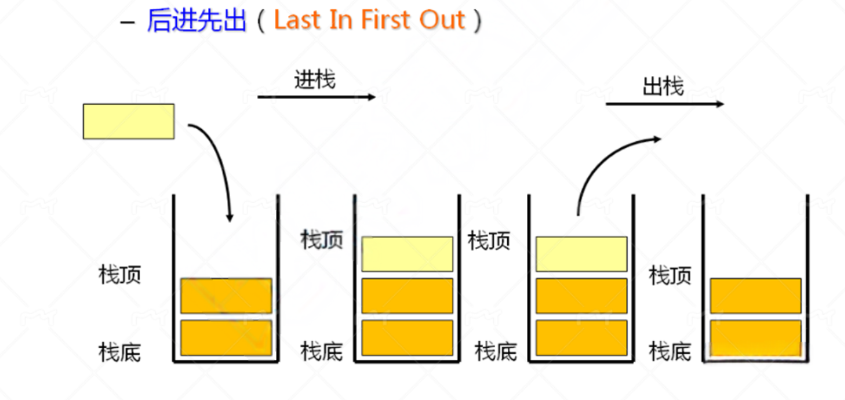
栈的核心特点是 "后进先出"，可以用生活中常见的场景类比理解：比如一摞叠放的盘子，只能从最上面取盘子，也只能往最上面放盘子，先放的盘子会被压在最下面，最后才能被取出。

1.1 栈的实现

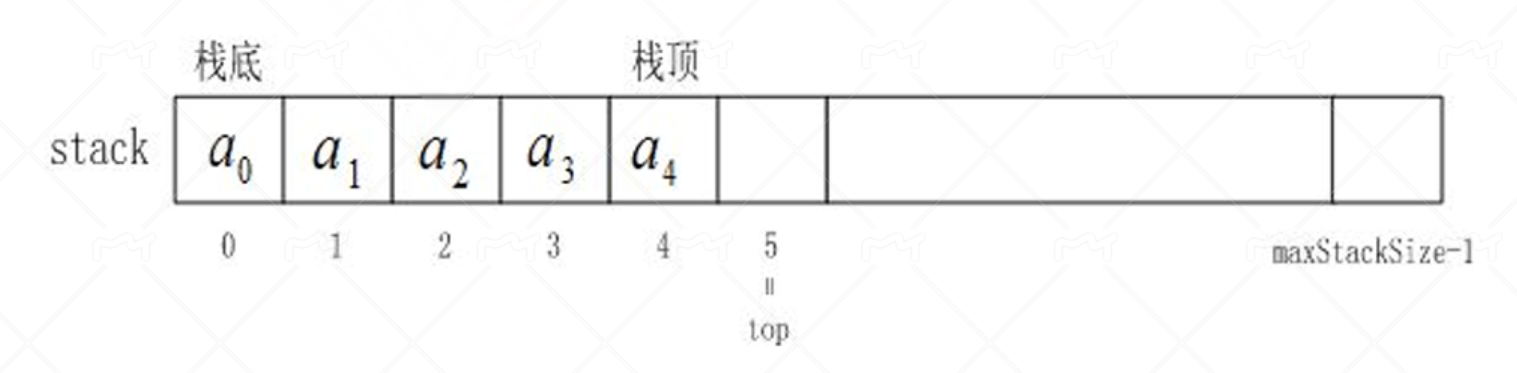
栈的实现方式有多种，主要可以利用数组和链表实现，相比而言利用数组实现开销更小。使用数组实现时我们可以可以将栈理解为一个特殊的顺序表，我们将这个顺序表的第一个元素所在的位置当作栈底，最后一个元素所在的位置当作栈顶。数据只能从栈顶出栈或者入栈，对应到顺序表我们只需要实现尾插与尾删即可。

cpp 复制代码 
//Stack.h
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>
typedef int SLDatetype;
typedef struct Stack
{
    //利用动态数组实现动态栈结构
	SLDatetype* a;
    //栈顶的位置（有效数据的个数）
	size_t top;
    //空间总大小
	size_t capacity;
}ST;

//初始化和销毁
void Init(ST* ch);
void Destory(ST* ch);
//入栈和出栈
void ST_push(ST* ch, SLDatetype x);
void ST_pop(ST* ch);
//取栈顶的数据
SLDatetype ST_top(ST* ch);
//判空
bool STEmpty(ST* ch);
//获取数据个数：
size_t ST_size(ST* ch);
cpp 复制代码 
//Stack.c
#include"Stack.h"
void Init(ST* ch)
{
	assert(ch);
	ch->a = NULL;
	ch->capacity = ch->top = 0;
}
void Destory(ST* ch)
{
	assert(ch);
	free(ch->a);
	ch->a = NULL;
	ch->capacity = ch->top = 0;
}
void ST_push(ST* ch, SLDatetype x)//入栈（压栈）
{
	assert(ch);
	//判断空间够不够：
	if (ch->top == ch->capacity)
	{
		size_t newcapacity = ch->capacity == 0 ? 4 : 2 * ch->capacity;
		SLDatetype* temp = (SLDatetype*)realloc(ch->a,newcapacity*sizeof(SLDatetype));
		if (temp==NULL)
		{
			perror("realloc fail");
			return;
		}
		ch->a = temp;
		ch->capacity = newcapacity;
	}
	ch->a[ch->top] = x;
	ch->top++;
}
void ST_pop(ST* ch)
{
	assert(ch);
	assert(ch->top>0);
	ch->top--;
}
SLDatetype ST_top(ST* ch)//取栈顶的元素
{
	assert(ch);
	assert(ch->top>0);
	return (ch->a[ch->top-1]);
}
bool STEmpty(ST* ch)
{
	assert(ch);
	return ch->top == 0;
}
size_t ST_size(ST* ch)
{
	assert(ch);
	return ch->top;
}

测试运行：

cpp 复制代码 
#include"Stack.h"

void PrintStack(ST* st)
{
	for (int i = 0; i < st->top; i++)
	{
		printf("%d ",st->a[i]);
	}
	printf("\n");
}
int main()
{
	ST st;
	Init(&st);
	ST_push(&st, 1);
	ST_push(&st, 2);
	ST_push(&st, 3);
	ST_push(&st, 4);
	ST_push(&st, 5);
	ST_push(&st, 6); 
	PrintStack(&st);

	printf("%d\n", ST_top(&st));//获取栈顶数据
	ST_pop(&st);//删除栈顶数据
	PrintStack(&st);

	printf("%d\n", ST_top(&st));
	ST_pop(&st);
	PrintStack(&st);

	printf("%d\n", ST_top(&st));
	ST_pop(&st);
	PrintStack(&st);

	Destory(&st);
	return 0;
}

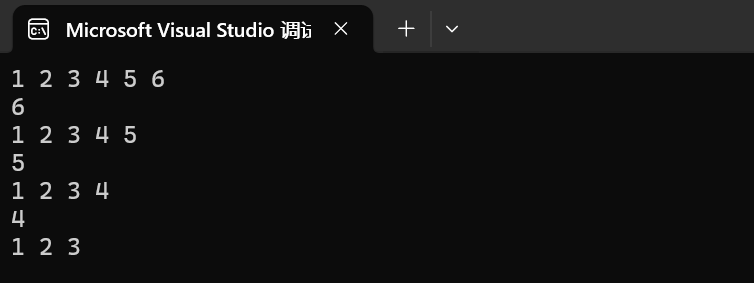
1.2 栈的应用（非递归快排）

在实现快速排序时，我们利用了分治递归的思想。但是我们需要明确的是递归函数的执行依赖系统调用栈（也叫 "程序栈"），系统会自动为每次递归调用保存 "上下文"。

以数组 [6, 3, 8, 5, 2] 的递归快排为例，系统栈的变化过程：

  1. 调用 quick_sort_recursive(arr, 0, 4) → 系统栈压入 (0,4)→出栈数据(0,4)处理（基准值为最左边的数6）
  2. 第一次快排后得到 [2, 3, 5, 6, 8]，递归调用左子数组 (0,2) → 栈压入 (0,2)；
  3. 处理 (0,2) 分区后，递归调用 (1,2) → 栈压入 (1,2)；
  4. 处理 (1，2) 后，无更多递归，系统栈依次弹出 再处理右子数组 (4,4) → 最后弹出 (0,4)。

简单说：递归 = 系统自动用栈保存待处理的子问题 + 按 "后进先出" 处理子问题。

当我们将递归改为非递归时本质上就是模拟程序处理递归函数的栈结构的入栈和出栈流程。

cpp 复制代码 
//快慢双指针法
int QSortOnce2(int* arr, int left, int right)
{
	int keyi = left;
	int prev = left;
	int cur = left + 1;
	while (cur<=right)
	{
		if (arr[cur] < arr[keyi])
		{
			prev++;
			Swap(&arr[cur], &arr[prev]);
		}
		cur++;
	}
	Swap(&arr[keyi], &arr[prev]);
	return prev;
}
//非递归快速排序
void QuickSortNonR(int* arr, int left, int right)
{
	ST st;
	Init(&st);
	ST_push(&st, right);
	ST_push(&st, left);
	while (!STEmpty(&st))
	{
		int begin= ST_top(&st);
		ST_pop(&st);
		int end= ST_top(&st);
		ST_pop(&st);
        
		int pos=QSortOnce2(arr, begin, end);
        if (pos+1 < end)
		{
			ST_push(&st, end);
			ST_push(&st, pos+1);
		}
		if (pos-1 > begin)
		{
			ST_push(&st, pos-1);
			ST_push(&st, begin);
		}
		
	}
	Destory(&st);
}

主函数QuickSortNonR的执行流程如下：

  • 初始化栈：先把整个数组的边界 (left, right) 压入栈（注意压栈顺序是先 right 再 left，这样弹出时才能先拿到 begin，再拿到 end）
  • 循环处理栈：只要栈不为空，就弹出一组 (begin, end)
  • 分区操作：调用 QSortOnce2 对当前子数组分区，得到基准值的位置 pos
  • 压入子数组边界：如果右子数组 [pos+1, end] 长度大于 1，也把它的边界压入栈；如果左子数组 [begin, pos-1] 长度大于 1，就把它的边界压入栈
  • 销毁栈：排序完成后释放栈的资源

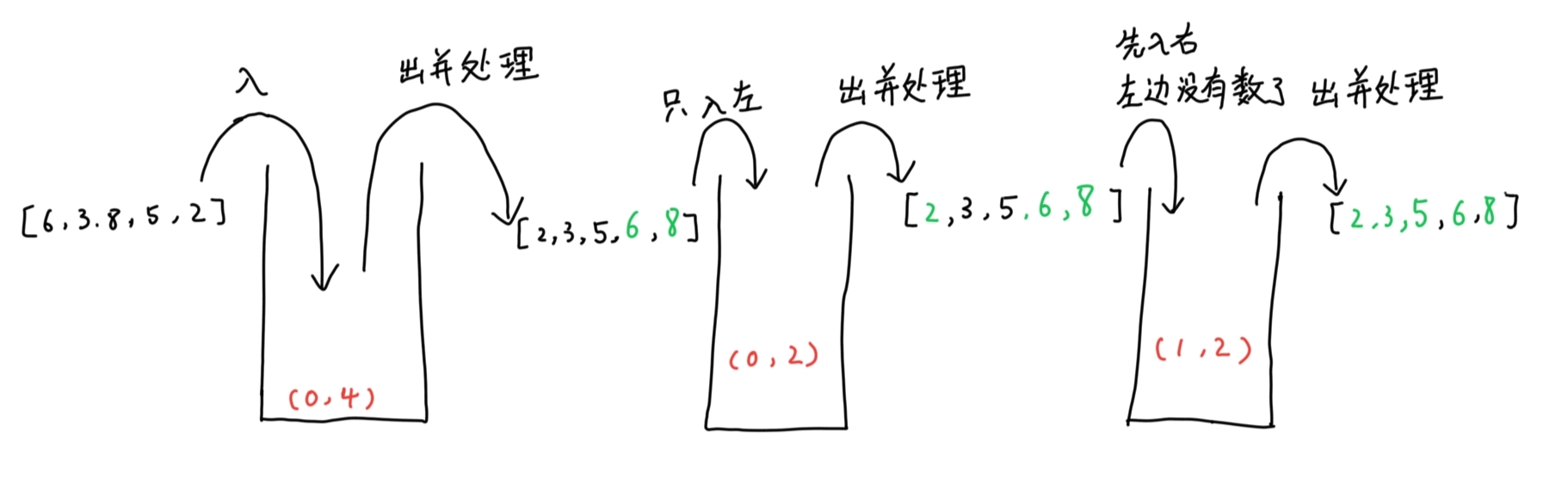
同样是数组[6, 3, 8, 5, 2]我们采用上述非递归快排时，下图则描述了程序控制的出栈与入栈流程：

二、什么是队列

队列是一种线性数据结构 ，遵循 FIFO（First In, First Out，先进先出） 的原则 ------ 就像日常生活中排队买东西：第一个排队的人第一个结账离开，最后来的人排在队尾，必须等前面的人都处理完才能轮到。

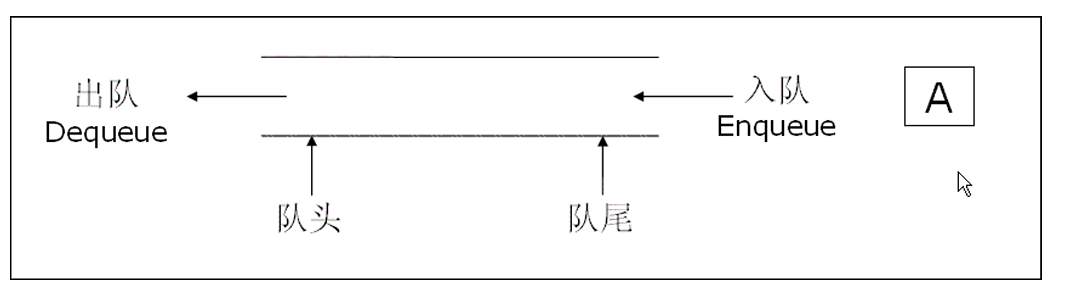
队列的操作围绕 队首出、队尾入 展开，核心操作只有 4 个

  1. 入队：将元素添加到队列的尾部（队尾），如果队列满了（比如固定长度的队列），会触发 "队列满" 异常（或返回失败）。
  2. 出队：从队列的头部移除并返回元素，如果队列为空，会触发 "队列空" 异常（或返回失败）。
  3. 查看队首：返回队首元素，但不移除它，用于查看 "下一个要处理的元素"。
  4. 判空：判断队列是否为空，是队列操作的前置检查（避免出队时操作空队列）。

2.1 队列的实现

队列的实现也有两种方式，数组和链表。我们试想一下，当用数组实现队列的时候从队尾入队列非常方便，直接在后边插入数据然后递增有效数据即可，但是当我们从队头出队列的时候就不可避免地移动整个数据。如果整个队列地数据存储量非常大那么就会导致每个数据都要进行移动，性能严重下降。

那么当我们使用链表怎么样呢？使用链表实现队列的时候，出队和入队都非常方便只需要更改节点的指针即可，唯一头疼的一点是当队尾入队时必须遍历一遍链表来找尾。但是这个问题可以解决，我们可以重新定义一个结构体，这个结构体用来动态地存储链表的头尾节点的指针，当需要入队或者出队的时候访问该结构体就可以直接找到头尾节点的指针进行插入或者删除操作，当进行完操作之后再更新该结构体头尾节点指针，方便下一次操作。

cpp 复制代码 
#include<stdlib.h>
#include<stdio.h>
#include<stdbool.h>
#include<assert.h>

typedef int QueueDataType;
typedef struct QueueNode
{
	struct QueueNode* _next;
	QueueDataType _data;
}QNode;

typedef struct Queue
{
	QNode* _phead;
	QNode* _ptail;
	int _size;
}Queue;

void QueueInit(Queue* pq);
//队列的销毁
void QueueDestory(Queue* pq);
//队尾入队
void QueuePush(Queue* pq, QueueDataType x);
// 队头删除
void QueuePop(Queue* pq);
//获取队头或队尾的数据
QueueDataType QueueFrant(Queue* pq);
QueueDataType QueueBack(Queue* pq);
//队列判空
bool QueueEmpty(Queue* pq);
cpp 复制代码 
#include"Queue.h"

void QueueInit(Queue* pq)
{
	assert(pq);
	pq->_phead = NULL;
	pq->_ptail = NULL;
	pq->_size = 0;
}
//队列的销毁
void QueueDestory(Queue* pq)
{
	assert(pq);
	QNode* cur = pq->_phead;
	while (cur)
	{
		QNode* next = cur->_next;
		free(cur);
		cur = next;
	}
	pq->_phead = pq->_ptail = NULL;
	pq->_size = 0;
}
//队尾入队
void QueuePush(Queue* pq, QueueDataType x)
{
	//创建新节点
	assert(pq);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		printf("创建新节点失败！！");
		return;
	}
	newnode->_data = x;
	newnode->_next = NULL;
	//队尾入队
	if (pq->_ptail == pq->_phead && pq->_phead == NULL)
	{
		//一个节点也没有
		pq->_phead = newnode;
		pq->_ptail = newnode;
	}
	else
	{
		//一个节点即以上
		pq->_ptail->_next = newnode;
		pq->_ptail = newnode;
	}
	pq->_size++;
}

// 队头删除
void QueuePop(Queue* pq)
{
	assert(pq);
	assert(pq->_size != 0);
	QNode* next = pq->_phead;
	if (pq->_phead->_next == NULL)
	{
		//只有一个节点
		pq->_phead = pq->_ptail = NULL;
	}
	else
	{
		//一个节点以上
		pq->_phead = pq->_phead->_next;
	}
	free(next);
	pq->_size--;
}

//获取队头或队尾的数据
QueueDataType QueueFrant(Queue* pq)
{
	assert(pq);
	assert(pq->_size != 0);
	return pq->_phead->_data;
}
QueueDataType QueueBack(Queue* pq)
{
	assert(pq);
	assert(pq->_size != 0);
	return pq->_ptail->_data;
}
//队列判空
bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->_size == 0;
}

代码测试：

cpp 复制代码 
#include"Queue.h"
#include<assert.h>
void PrintQue(Queue* queue)
{
	assert(queue);
	QNode* cur = queue->_phead;
	while (cur)
	{
		printf("%d ",cur->_data);
		cur = cur->_next;
	}
	printf("\n");
}

int main()
{
	Queue myqueue;
	QueueInit(&myqueue);
	QueuePush(&myqueue, 3);
	QueuePush(&myqueue, 6);
	QueuePush(&myqueue, 9);
	QueuePush(&myqueue, 2);
	QueuePush(&myqueue, 5);
	QueuePush(&myqueue, 8);
	QueuePush(&myqueue, 1);
	PrintQue(&myqueue);

	printf("%d\n", QueueFrant(&myqueue));
	QueuePop(&myqueue);
	PrintQue(&myqueue);

	printf("%d\n", QueueFrant(&myqueue));
	QueuePop(&myqueue);
	PrintQue(&myqueue);

	QueueDestory(&myqueue);
	return 0;
}

2.2 队列的应用（环形队列的生产消费模型）

https://blog.csdn.net/yue_2899799318/article/details/155011960?fromshare=blogdetail&sharetype=blogdetail&sharerId=155011960&sharerefer=PC&sharesource=yue_2899799318&sharefrom=from_link

三、总结一下

栈和队列都是线性数据结构 （元素排成一条线），核心区别在于元素的存取顺序：

  1. 栈（Stack）：后进先出（LIFO, Last In First Out）

比喻：像叠盘子，最后放上去的盘子最先被拿走；也像浏览器的后退按钮（最后打开的页面最先关闭）。

核心操作：

  • 入栈（把元素放到栈顶）
  • 出栈（移除并返回栈顶元素）
  • 查看栈顶元素（不删除）
  • 判断栈是否为空
  1. 队列（Queue）：先进先出（FIFO, First In First Out）

比喻：像排队买奶茶，第一个排队的人最先买到；也像打印机的任务队列（先提交的任务先打印）。

核心操作：

  • 入队（把元素加到队列尾部）
  • 出队（移除并返回队列头部元素）
  • 查看队首元素（不删除）
  • 判断队列是否为空
相关推荐
xqqxqxxq2 小时前
认识数据结构之——图 构建图与应用
数据结构·python·算法
陌上丨2 小时前
Redis常用的数据类型有哪些？Zset的底层数据结构是什么？
数据结构·数据库·redis
FMRbpm2 小时前
邻接矩阵练习1--------LCP 07.传递信息
数据结构·c++·算法·leetcode·深度优先·新手入门
郝学胜-神的一滴3 小时前
Linux Socket编程核心：深入解析sockaddr数据结构族
linux·服务器·c语言·网络·数据结构·c++·架构
IUGEI4 小时前
从原理到落地：DAG在大数据SLA中的应用
java·大数据·数据结构·后端·算法
云深麋鹿4 小时前
五.排序笔记
c语言·数据结构·算法·排序算法
福楠12 小时前
C++ STL | map、multimap
c语言·开发语言·数据结构·c++·算法
Sarvartha12 小时前
二分查找学习笔记
数据结构·c++·算法
谦宸、墨白15 小时前
从零开始学C++：二叉树进阶
开发语言·数据结构·c++
热门推荐
01GitHub 镜像站点02【网络安全测试】Burp Suite工具使用说明、配置及常见问题（有关必回）03OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)04Claude Code Skills 实用使用手册05UV安装并设置国内源06struts2 XML外部实体注入漏洞复现（CVE-2025-68493）07Open Code教程（四）| 高级配置与集成08在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）09AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南10Linux下V2Ray安装配置指南