神经网络的学习

核心结论：神经网络的 "学习" 本质是通过数据自动找到最优权重参数 ，核心逻辑是用损失函数判断预测误差，用梯度下降法调整参数，最终让模型能精准完成任务。

一、学习的核心目标

神经网络之所以能 "学习"，关键是找到一组最优的权重参数（相当于模型的 "记忆"）。

权重就像 "调节旋钮"：每个神经元之间的连接都有一个权重，权重大小决定信号传递的强弱。
学习的目标：通过数据调整这些 "旋钮"，让模型的预测结果尽可能接近真实答案。

二、判断误差的 "标尺"：损失函数

要调整权重，首先得知道 "当前模型有多差"，这就需要损失函数（相当于 "误差标尺"）。

1. 常见的 "标尺" 类型

均方误差（MSE） ：适合预测连续值（比如房价、温度），计算预测值和真实值之间差的平方平均值。
- 通俗理解：像用尺子量差距，差距越大，"惩罚" 越重（平方后放大误差）。

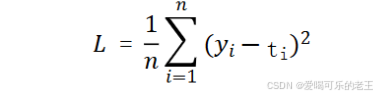
代码实现如下：

复制代码

def mean_square_error(y, t):  # y为预测值，t为真实值
    return 0.5 * np.sum((y-t)**2)

交叉熵误差 ：适合分类任务（比如识别手写数字、判断图片类别），重点惩罚 "预测对的概率太低" 的情况。
- 通俗理解：比如模型把 "5" 误判为 "3" 且概率很高，交叉熵会给出很大的误差值，督促模型改进。

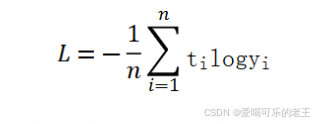
具体代码实现：

复制代码

def cross_entropy_error(y, t):
    #对于一条数据的情况，转换为二维结果
    if y.ndim == 1:
        t = t.reshape(1, -1)  #转换为二维
        y = y.reshape(1, -1)
    #如果t是独热编码，转换为解标签
    if t.size == y.size:
        t = t.argmax(axis=1)    #获取最大值的索引
    n = y.shape[0]
    return -np.sum(np.log(y[np.arange(n), t] + 1e-7)) / n

2. 不同任务选不同 "标尺"

二分类（是 / 否、正 / 负）：用二元交叉熵损失。
多分类（识别 0-9 数字、多种水果）：用多类交叉熵损失。
回归（预测具体数值）：用均方误差（MSE）或平均绝对误差（MAE）。

三、调整参数的 "方法"：梯度下降

知道了误差，下一步就是调整权重减少误差，核心方法是梯度下降。

1. 梯度：误差变化的 "方向标"

梯度是损失函数的导数，告诉我们："调整哪个权重、往哪个方向调，能让误差下降最快"。
通俗理解：就像下山时，梯度指向 "最陡的下坡方向"，跟着梯度走，能最快走到山底（误差最小）。

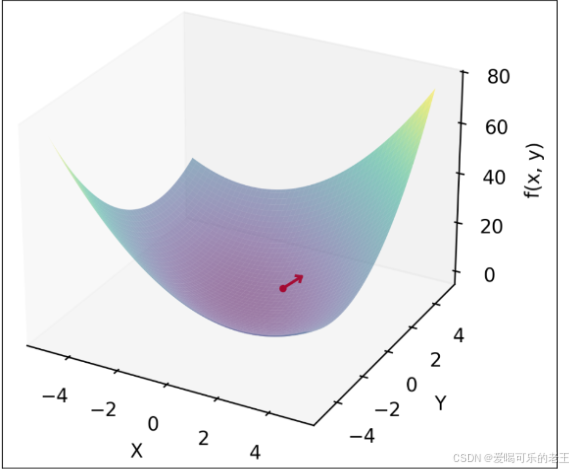
需要注意的是，梯度代表的其实是函数值增大最快的方向；在实际应用中，我们需要寻找损失函数的最小值，所以一般选择 负梯度向量

利用数值微分可简单实现梯度代码：

复制代码

#梯度
def _numerical_gradient(f, x):
    h = 1e-4 # 0.0001
    grad = np.zeros_like(x)   # 创建一个和x一样大小的零向量
    for idx in range(x.size):
        tmp_val = x[idx]        # 保存当前值
        x[idx] = float(tmp_val) + h     # 当前值加上微小值
        fxh1 = f(x)     # f(x+h)        # 计算f(x+h)
        x[idx] = tmp_val - h            # 还原当前值
        fxh2 = f(x)     # f(x-h)        # 计算f(x-h)
        grad[idx] =(fxh1 - fxh2) / (2*h)
        x[idx] = tmp_val  #
        #还原值
    return grad

2. 核心步骤（以随机梯度下降 SGD 为例）

随机选一批数据（mini-batch）：不用全量数据，选一小部分计算误差，又快又准。
算梯度：针对这批数据，计算每个权重对应的梯度。
调权重：沿着梯度的反方向（下坡方向），按一定步长调整权重。
重复迭代：反复做 1-3 步，直到误差降到满意水平。

3. 关键概念（训练时必懂）

学习率（η）：调整权重的 "步长"。太大容易 "走过头"，太小则学习太慢。
Epoch：模型完整看一遍所有训练数据的次数（比如训练 10 个 Epoch，就是把数据学 10 遍）。
Batch Size：每次选多少个样本计算梯度（比如 Batch Size=100，就是每次用 100 个样本）。
Iteration：每处理一个 Batch 并调整一次参数，就是一次迭代。

四、简单案例：手写数字识别的学习过程

初始状态：模型的权重是随机的，识别手写数字时误差很大（比如把 "8" 认成 "3"）。
计算误差：用交叉熵损失函数，算出 "把 8 认成 3" 的误差值。
算梯度：找到 "调整哪些权重，能让模型下次更可能认出 8"。
调权重：按学习率沿着梯度反方向调整权重。
重复迭代：用大量手写数字样本反复训练，误差越来越小，模型识别准确率越来越高。

五、核心总结

神经网络的学习 ="误差标尺"（损失函数）+"调整方法"（梯度下降）：

用损失函数量化 "预测有多差"；
用梯度找到 "怎么调权重能变好"；
反复迭代，直到模型能精准完成任务。