机器学习（三）：聚焦KNN算法距离度量、特征预处理与超参数选择

个人主页-爱因斯晨

文章专栏-机器学习

文章目录

- 个人主页-爱因斯晨
- 文章专栏-机器学习
- 一、距离度量
- 二、特征预处理
- - [2.1 归一化](#2.1 归一化)
  - [2.2 标准化](#2.2 标准化)
  - [2.3 核心差异对比](#2.3 核心差异对比)
  - - [2.3.1 KNN 算法选型核心建议](#2.3.1 KNN 算法选型核心建议)
    - - [1. 优先选「标准化」的场景（KNN 最常用）](#1. 优先选「标准化」的场景（KNN 最常用）)
      - [2. 优先选「归一化」的场景](#2. 优先选「归一化」的场景)
      - [3. 通用实战原则](#3. 通用实战原则)
- [三、KNN 核心超参数及影响](#三、KNN 核心超参数及影响)
- - 3.1超参数选择核心方法
  - - [3.1.1. 交叉验证（Cross Validation）](#3.1.1. 交叉验证（Cross Validation）)
    - [3.1.2. 网格搜索（Grid Search）](#3.1.2. 网格搜索（Grid Search）)
    - [3.1.3. 随机搜索（Random Search）](#3.1.3. 随机搜索（Random Search）)
  - [3.2实战：KNN 超参数选择（网格搜索 + 5 折交叉验证）](#3.2实战：KNN 超参数选择（网格搜索 + 5 折交叉验证）)
  - - [示例 1：鸢尾花数据集（基础版）](#示例 1：鸢尾花数据集（基础版）)
    - [示例 2：手写数字识别（进阶版，MNIST 子集）](#示例 2：手写数字识别（进阶版，MNIST 子集）)
  - 3.3超参数选择实战技巧
  - - [1. k 值选择技巧](#1. k 值选择技巧)
    - [2. 距离度量选择技巧](#2. 距离度量选择技巧)
    - [3. 权重方式选择技巧](#3. 权重方式选择技巧)
    - [4. 避免数据泄露](#4. 避免数据泄露)

一、距离度量

1.1欧式距离

直观的距离度量方法，两个点在空间中的距离一般都是指欧式距离。

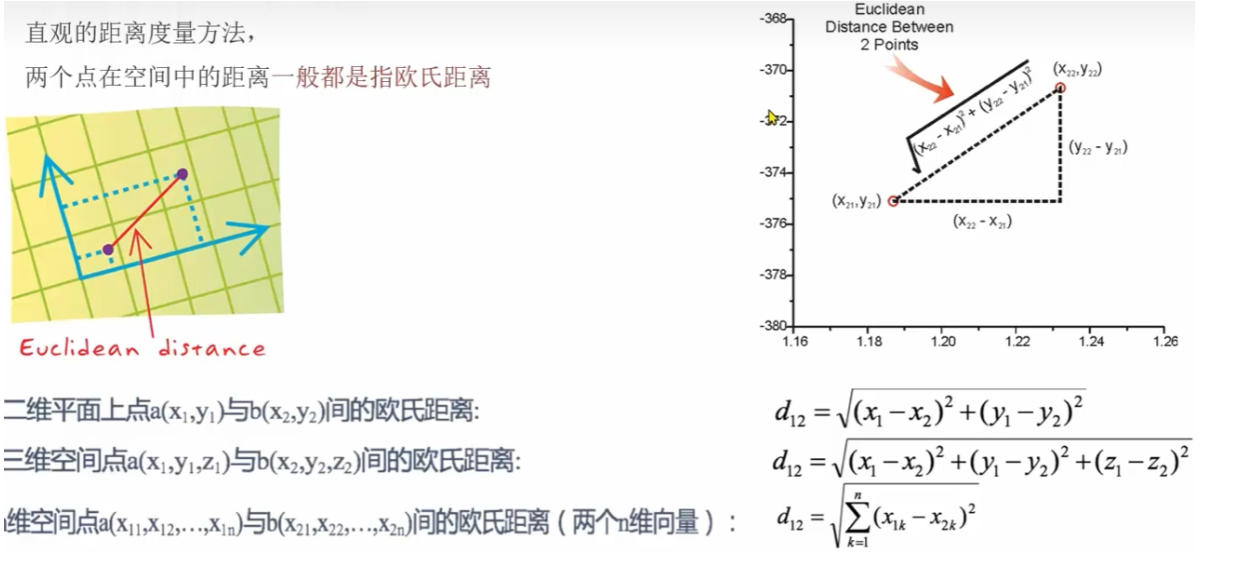
欧氏距离=对应维度差值平方和，开平方根

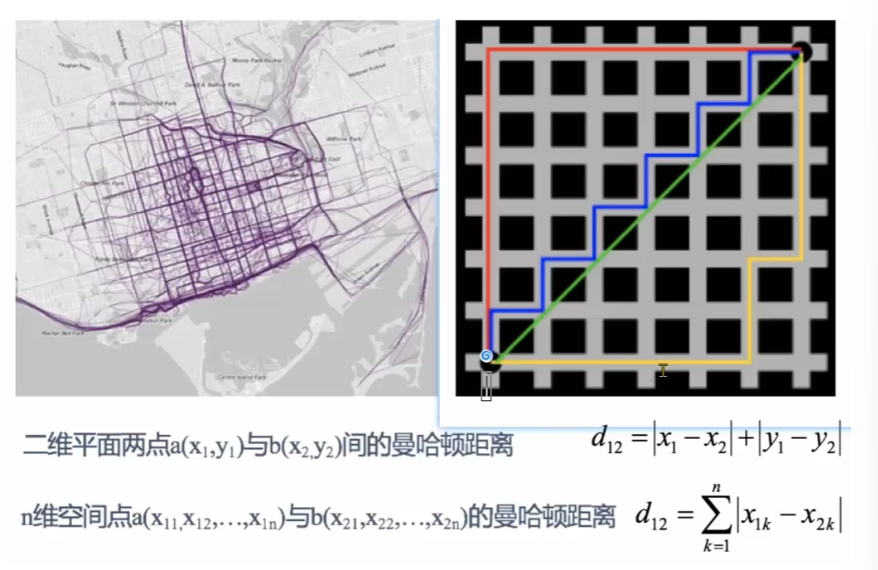
1.2曼哈顿距离

也称城市街区距离，曼哈顿城市特点：横平竖直

曼哈顿距离=对应维度差值的绝对值，求和

1.3切比雪夫距离

国际象棋中，国王可以直行、横行、斜行，所以国王走一步可以移动到相邻8个方格的任意一个。国王从格子（x1,y1）走到格子（x2,y2）最少需要多少步？这个距离就叫切比雪夫距离

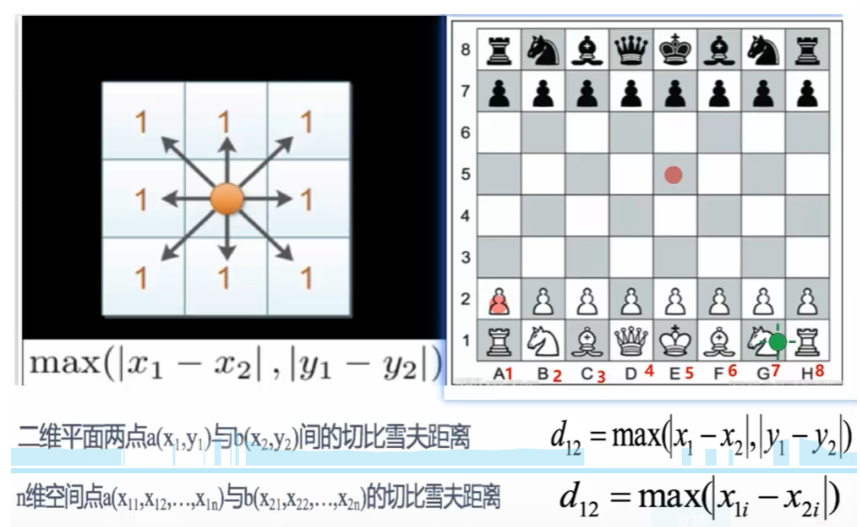
切比雪夫距离=对应纬度差值的绝对值，求最大值

1.4闵可夫斯基距离

不是一种新的距离的度量方式，是对多个距离度量公式的概括性的表述

两个n维变量a(x11,x12...xln)与b(x21,x22...x2n)

闵可夫斯基距离定义为：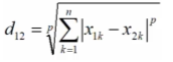

其中p是一个变参数：

当p=1时，就是曼哈顿距离。
当p=2时，就是欧氏距离
当p→∞，就是切比雪夫距离

根据p的不同，闵氏距离可表示某一类种的距离

二、特征预处理

为什么要做归一化和标准化

特征的单位或者相差较大，或者某特征的方差相比其他的特征要大出几个数量级，容易影响（支配）目标结果，使得一些模型（算法）无法学习到他的特征

2.1 归一化

通过对原始数据进行变换把数据映射到【mi,mx】默认为[0,1]之间

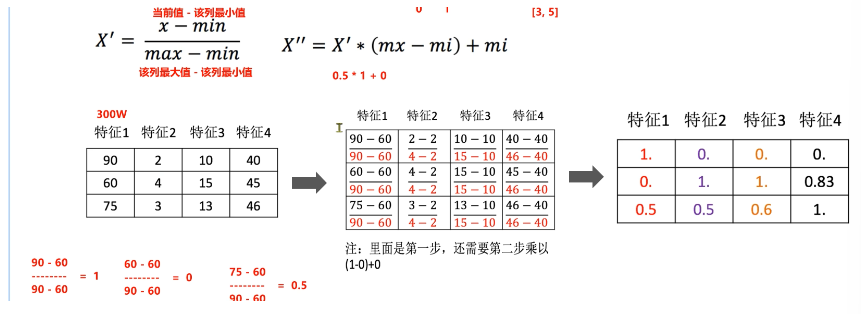
数据归一化API：sklearn.preprocessing.MinMaxScaler(feature_range=(0,1)...)

feature_range缩放区间（训练集）

fit_transform(X)将特征进行归一化缩放（测试集）

代码实现：

python 复制代码

import numpy as np
from sklearn.preprocessing import MinMaxScaler

# 1. 定义原始数据（对应图片中的300W数据）
data = np.array([
    [90, 2, 10, 40],
    [60, 4, 15, 45],
    [75, 3, 13, 46]
])
print("原始数据：")
print(data)
print("-" * 50)

# ---------------------- 方式1：手动实现归一化（对应图片公式） ----------------------
# 步骤1：计算每列的最小值和最大值
min_vals = data.min(axis=0)  # 按列求最小
max_vals = data.max(axis=0)  # 按列求最大

# 步骤2：第一步归一化（映射到[0,1]）
X_prime = (data - min_vals) / (max_vals - min_vals)

# 步骤3：第二步缩放（可选，示例映射到[0,1]，若需[3,5]则替换feature_range）
feature_range = (0, 1)
X_normalized_manual = X_prime * (feature_range[1] - feature_range[0]) + feature_range[0]

print("手动计算归一化结果：")
print(np.round(X_normalized_manual, 3))  # 保留3位小数，和图片结果一致
print("-" * 50)

# ---------------------- 方式2：sklearn API实现（推荐） ----------------------
# 初始化MinMaxScaler，指定缩放范围[0,1]（默认就是[0,1]，可省略）
scaler = MinMaxScaler(feature_range=(0, 1))

# 拟合数据并转换（fit计算min/max，transform执行归一化）
X_normalized_sklearn = scaler.fit_transform(data)

print("sklearn API归一化结果：")
print(np.round(X_normalized_sklearn, 3))
print("-" * 50)

# 验证：手动计算和API结果是否一致
print("手动计算与sklearn结果是否一致：", np.allclose(X_normalized_manual, X_normalized_sklearn))

# 扩展：若需映射到[3,5]，只需修改feature_range
scaler_35 = MinMaxScaler(feature_range=(3, 5))
X_normalized_35 = scaler_35.fit_transform(data)
print("\n映射到[3,5]的归一化结果：")
print(np.round(X_normalized_35, 3))

结果：

复制代码

原始数据：
[[90  2 10 40]
 [60  4 15 45]
 [75  3 13 46]]
--------------------------------------------------
手动计算归一化结果：
[[1.    0.    0.    0.   ]
 [0.    1.    1.    0.833]
 [0.5   0.5   0.6   1.   ]]
--------------------------------------------------
sklearn API归一化结果：
[[1.    0.    0.    0.   ]
 [0.    1.    1.    0.833]
 [0.5   0.5   0.6   1.   ]]
--------------------------------------------------
手动计算与sklearn结果是否一致： True

映射到[3,5]的归一化结果：
[[5. 3. 3. 3. ]
 [3. 5. 5. 4.666]
 [4. 4. 4.2 5. ]]

2.2 标准化

标准化也叫 Z-score 归一化，核心是将特征转换为均值为 0，标准差为 1 的分布，公式如下：

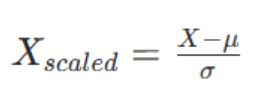
μ：该特征列的均值（mean）
σ：该特征列的标准差（standard deviation）

代码实现：

python 复制代码

import numpy as np
from sklearn.preprocessing import StandardScaler

# 1. 定义原始数据（与归一化案例一致，方便对比）
data = np.array([
    [90, 2, 10, 40],
    [60, 4, 15, 45],
    [75, 3, 13, 46]
])
print("原始数据：")
print(data)
print("-" * 60)

# ---------------------- 方式1：手动实现标准化（对应公式） ----------------------
# 步骤1：计算每列的均值和标准差
mean_vals = data.mean(axis=0)  # 按列求均值
std_vals = data.std(axis=0, ddof=0)  # 按列求标准差（ddof=0表示总体标准差，与sklearn一致）

# 步骤2：执行标准化计算
X_standard_manual = (data - mean_vals) / std_vals

print("手动计算标准化结果（保留3位小数）：")
print(np.round(X_standard_manual, 3))
print("-" * 60)

# ---------------------- 方式2：sklearn API实现（实战推荐） ----------------------
# 初始化StandardScaler（默认计算总体标准差，与手动实现一致）
scaler = StandardScaler()

# 拟合数据并转换（fit计算均值/标准差，transform执行标准化）
X_standard_sklearn = scaler.fit_transform(data)

print("sklearn API标准化结果（保留3位小数）：")
print(np.round(X_standard_sklearn, 3))
print("-" * 60)

# 验证：手动计算和API结果是否一致
print("手动计算与sklearn结果是否一致：", np.allclose(X_standard_manual, X_standard_sklearn))

# 扩展：查看标准化后的均值和标准差（验证是否符合「均值0，标准差1」）
print("\n标准化后每列均值（应接近0）：", np.round(X_standard_sklearn.mean(axis=0), 3))
print("标准化后每列标准差（应接近1）：", np.round(X_standard_sklearn.std(axis=0), 3))

# 实战关键：训练集和测试集的标准化（避免数据泄露）
print("\n=== 实战：训练集/测试集分离标准化 ===")
# 模拟划分训练集和测试集
train_data = data[:2]  # 前2行作为训练集
test_data = data[2:]   # 最后1行作为测试集

# 仅用训练集拟合scaler，再分别转换训练集和测试集
train_scaler = StandardScaler()
train_data_scaled = train_scaler.fit_transform(train_data)
test_data_scaled = train_scaler.transform(test_data)

print("训练集标准化结果：")
print(np.round(train_data_scaled, 3))
print("测试集标准化结果（用训练集的均值/标准差）：")
print(np.round(test_data_scaled, 3))

结果实现：

复制代码

原始数据：
[[90  2 10 40]
 [60  4 15 45]
 [75  3 13 46]]
------------------------------------------------------------
手动计算标准化结果（保留3位小数）：
[[ 1.061 -1.0   -1.225 -1.373]
 [-1.061  1.0    1.225  0.458]
 [ 0.     0.     0.     0.915]]
------------------------------------------------------------
sklearn API标准化结果（保留3位小数）：
[[ 1.061 -1.0   -1.225 -1.373]
 [-1.061  1.0    1.225  0.458]
 [ 0.     0.     0.     0.915]]
------------------------------------------------------------
手动计算与sklearn结果是否一致： True

标准化后每列均值（应接近0）： [ 0. -0.  0.  0.]
标准化后每列标准差（应接近1）： [1. 1. 1. 1.]

=== 实战：训练集/测试集分离标准化 ===
训练集标准化结果：
[[ 1. -1. -1. -1.]
 [-1.  1.  1.  1.]]
测试集标准化结果（用训练集的均值/标准差）：
[[ 0.  0.  0.  1.225]]

2.3 核心差异对比

对比维度	归一化（Min-Max Scaling）	标准化（Z-Score）
核心公式	X′=max−minX−min（映射到 [0,1]）	X′=σX−μ（均值 0，标准差 1）
数值范围	固定区间 [0,1]（可自定义）	无固定区间，围绕 0 分布
异常值影响	敏感（极值会压缩其他数据）	鲁棒（均值 / 标准差受异常值影响小）
数据分布要求	无严格要求，适合均匀分布	适合近似正态分布，或有少量异常值
KNN 距离影响	所有特征被等比例压缩到同一尺度，距离计算公平	特征按分布标准化，消除量纲影响，距离更合理

2.3.1 KNN 算法选型核心建议

1. 优先选「标准化」的场景（KNN 最常用）

数据存在异常值（如某特征有极端大 / 小值，归一化会被极值 "带偏"）；
特征量纲差异极大（如一个特征是 "收入（万）"，一个是 "年龄（岁）"）；
数据近似正态分布（如身高、体重、成绩等连续型特征）；
需结合其他模型（如 SVM、逻辑回归），标准化是通用预处理方式。

2. 优先选「归一化」的场景

数据无异常值 ，分布均匀（如像素值 0-255、评分 0-10 等固定区间数据）；
特征本身就是比例 / 百分比（无需保留分布信息，仅需统一尺度）；
需明确的数值区间（如后续需将特征映射到 [0,1] 做概率计算）。

3. 通用实战原则

KNN 必做缩放：无论选哪种，都要做，否则量纲大的特征会 "支配" 距离计算，导致模型失效；
先看数据：先做数据探索（看分布、查异常值），再选方法；
训练集优先 ：缩放时仅用训练集计算 min/max 或均值 / 标准差，再转换测试集，避免数据泄露。

KNN 的超参数直接决定模型性能，核心超参数 是k 值（近邻数） 、距离度量 、权重方式 ，选择核心思路是用交叉验证评估不同超参数组合，选最优解，下面从原理到实战全解析。

三、KNN 核心超参数及影响

超参数	含义	对 KNN 的影响
n_neighbors (k)	选择的近邻样本数	k 过小：过拟合，对噪声敏感；k 过大：欠拟合，模型泛化能力差
metric	距离度量方式	欧氏距离（默认）：适合连续型特征；曼哈顿距离：适合特征有不同量纲；余弦距离：适合文本 / 高维稀疏特征
weights	近邻权重方式	uniform：等权重投票；distance：按距离加权（距离越近权重越大），适合数据有噪声的场景
algorithm	近邻搜索算法	auto：自动选择；ball_tree：适合高维数据；kd_tree：适合低维数据；brute：暴力搜索，适合小样本

3.1超参数选择核心方法

3.1.1. 交叉验证（Cross Validation）

核心思想：将训练集划分为 k 折（如 5 折 / 10 折），轮流用 k-1 折训练、1 折验证，取平均准确率作为模型性能指标，避免单次划分的偶然性。

优势：充分利用训练集，评估更稳定，防止过拟合 / 欠拟合；
常用折数：5 折、10 折（样本量小选 10 折，样本量大选 5 折）。

3.1.2. 网格搜索（Grid Search）

核心思想：预设超参数的候选组合，遍历所有组合，结合交叉验证找到最优超参数。

优势：覆盖所有候选组合，结果可靠；
劣势：候选组合多则计算量大，适合超参数少的场景（KNN 超参数少，完美适配）。

3.1.3. 随机搜索（Random Search）

核心思想：从超参数候选空间中随机采样组合，结合交叉验证评估，适合超参数多、网格搜索计算量过大的场景（KNN 一般用网格搜索即可）。

3.2实战：KNN 超参数选择（网格搜索 + 5 折交叉验证）

以手写数字识别 （MNIST 子集）和鸢尾花数据集 为例，用sklearn实现超参数选择，代码可直接复用。

示例 1：鸢尾花数据集（基础版）

python 复制代码

import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score

# 1. 数据加载与预处理（KNN必做标准化）
iris = load_iris()
X, y = iris.data, iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 标准化（消除量纲影响）
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

# 2. 定义KNN模型与超参数候选空间
knn = KNeighborsClassifier()
# 预设超参数候选组合（核心：k值、距离、权重）
param_grid = {
    'n_neighbors': [3, 5, 7, 9, 11],  # 候选k值（奇数避免投票平局）
    'metric': ['euclidean', 'manhattan', 'cosine'],  # 候选距离
    'weights': ['uniform', 'distance']  # 候选权重方式
}

# 3. 网格搜索+5折交叉验证（核心）
grid_search = GridSearchCV(
    estimator=knn,  # 待调参模型
    param_grid=param_grid,  # 超参数候选空间
    cv=5,  # 5折交叉验证
    scoring='accuracy',  # 评估指标：准确率
    n_jobs=-1  # 并行计算，加速
)
# 拟合训练集
grid_search.fit(X_train_scaled, y_train)

# 4. 输出最优结果
print("最优超参数组合：", grid_search.best_params_)
print("交叉验证最优准确率：", round(grid_search.best_score_, 4))

# 5. 用最优模型测试
best_knn = grid_search.best_estimator_
y_pred = best_knn.predict(X_test_scaled)
print("测试集准确率：", round(accuracy_score(y_test, y_pred), 4))

示例 2：手写数字识别（进阶版，MNIST 子集）

python 复制代码

from sklearn.datasets import load_digits
import matplotlib.pyplot as plt

# 1. 加载手写数字数据（8x8像素，10分类）
digits = load_digits()
X, y = digits.data, digits.target
print("数据形状：", X.shape)  # (1797, 64)，1797个样本，64个特征

# 数据划分与标准化
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

# 2. 超参数网格搜索（k值范围扩大，适配复杂数据）
knn = KNeighborsClassifier()
param_grid = {
    'n_neighbors': [1, 3, 5, 7, 9, 11, 13],
    'metric': ['euclidean', 'manhattan'],
    'weights': ['uniform', 'distance']
}

# 网格搜索+10折交叉验证（样本量更大，用10折更稳定）
grid_search = GridSearchCV(knn, param_grid, cv=10, scoring='accuracy', n_jobs=-1)
grid_search.fit(X_train_scaled, y_train)

# 3. 结果输出
print("最优超参数：", grid_search.best_params_)
print("交叉验证最优准确率：", round(grid_search.best_score_, 4))

# 测试集评估
best_knn = grid_search.best_estimator_
y_pred = best_knn.predict(X_test_scaled)
print("手写数字测试集准确率：", round(accuracy_score(y_test, y_pred), 4))

# 可视化：k值与准确率的关系（辅助理解k的影响）
k_range = [1, 3, 5, 7, 9, 11, 13]
cv_scores = []
for k in k_range:
    knn_temp = KNeighborsClassifier(n_neighbors=k, metric='euclidean', weights='distance')
    scores = cross_val_score(knn_temp, X_train_scaled, y_train, cv=10, scoring='accuracy')
    cv_scores.append(scores.mean())

plt.plot(k_range, cv_scores, 'o-')
plt.xlabel('k值')
plt.ylabel('交叉验证准确率')
plt.title('k值对KNN性能的影响')
plt.show()

3.3超参数选择实战技巧

1. k 值选择技巧

优先选奇数：避免二分类时投票平局（多分类也可减少平局概率）；
候选范围：从 1 开始，到训练集样本数的平方根（如训练集 1000 个样本，k 候选到 30 左右）；
观察趋势 ：k 增大，准确率先升后降，峰值对应的 k 为最优（过小过拟合，过大欠拟合）。

2. 距离度量选择技巧

连续型特征（如鸢尾花、手写数字）：优先欧氏距离；
特征量纲差异大 / 有异常值：曼哈顿距离（对极值不敏感）；
高维稀疏特征（如文本 TF-IDF）：余弦距离（忽略向量长度，关注方向）。

3. 权重方式选择技巧

数据无噪声、分布均匀：uniform（等权重），计算简单；
数据有噪声、样本分布不均：distance（距离加权），减少噪声影响。

4. 避免数据泄露

超参数选择仅用训练集 （网格搜索的交叉验证也是在训练集内划分），测试集仅用于最终评估；
分类也可减少平局概率）；
候选范围：从 1 开始，到训练集样本数的平方根（如训练集 1000 个样本，k 候选到 30 左右）；
观察趋势 ：k 增大，准确率先升后降，峰值对应的 k 为最优（过小过拟合，过大欠拟合）。