1、简介
现实世界的工程优化问题通常极具挑战性,因为可行区域狭窄、局部最优和复杂的约束。元启发式算法(MA)因其全局搜索能力、灵活性和适应性而在解决这些问题方面显示出希望。然而,MA的一个关键挑战是有效平衡全局搜索(探索)和局部搜索(开发)阶段,这极大地影响了收敛的效率和精度。许多MA需要针对特定问题进行调整来控制收敛行为,从而增加了计算成本和实施工作量。此外,现有的改进通常是针对特定问题量身定制的,缺乏通用性、鲁棒性和可扩展性方面的全面验证。
为了克服这些限制,本文提出了一种新的具有增强适应性的高性能优化算法,命名为三国优化算法,其灵感来自中国三国时期的历史动态。我们将MA的关键组成部分------如人口初始化、探索和开发------与四个历史阶段进行了类比:力量的上升、联合对抗、三足鼎立和全国团结。King采用了一种新的强化收敛机制来系统地指导搜索过程,同时保持探索和开发之间的有效平衡,从而实现快速高效的收敛。此外,还引入了一种动态的、基于容差的约束处理技术,以增强其解决复杂约束问题的能力。
2. 三国优化算法 (Three-kingdom optimization algorithm)
KING的核心优化过程包含四个不同的阶段:势力崛起 (AOM) 、联合对抗 (JC) 、三足鼎立 (TLT) 和全国统一 (WCU)。在 AOM 阶段,涌现出具有不同影响力水平的各种势力。其中,最强大的三个势力固化为不同的国家。在 JC 阶段,两个较弱的国家结盟以对抗主导国家。TLT 阶段的特点是三个国家之间的力量达到相对均衡。它们相互制衡,同时独立发展能力、吸引周边势力并增强各自的实力。在演化的后期,过程过渡到 WCU 阶段。三个国家逐渐被一个占主导地位的国家吞并,形成一个统一的实体。这个统一的主权对所有势力实行中央集权治理。
2.1. 种群初始化方法:势力崛起 (AOM)
在 AOM 中,KING 随机生成 N 个具有不同位置和不同实力的实体。每个实体包含 D 个影响国家实力的不同元素,例如经济、军事、政治、科技和自然资源。然后通过评估确定三个最强大的实体,对应于魏、蜀汉和东吴三个国家。对于初始化,KING 采用随机初始化方法,如公式 (1) 所示:
X = L + θ ∘ ( U − L ) X = L + \theta \circ (U - L) X=L+θ∘(U−L)
X = [ z 1 , 1 z 1 , 2 ⋯ z 1 , D − 1 z 1 , D z 2 , 1 z 2 , 2 ⋯ z 2 , D − 1 z 2 , D ⋮ ⋮ ⋱ ⋮ ⋮ z N − 1 , 1 z N − 1 , 2 ⋯ z N − 1 , D − 1 z N − 1 , D z N , 1 z N , 2 ⋯ z N , D − 1 z N , D ] (1) X = \begin{bmatrix} z_{1,1} & z_{1,2} & \cdots & z_{1,D-1} & z_{1,D} \\ z_{2,1} & z_{2,2} & \cdots & z_{2,D-1} & z_{2,D} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ z_{N-1,1} & z_{N-1,2} & \cdots & z_{N-1,D-1} & z_{N-1,D} \\ z_{N,1} & z_{N,2} & \cdots & z_{N,D-1} & z_{N,D} \\ \end{bmatrix} \tag{1} X= z1,1z2,1⋮zN−1,1zN,1z1,2z2,2⋮zN−1,2zN,2⋯⋯⋱⋯⋯z1,D−1z2,D−1⋮zN−1,D−1zN,D−1z1,Dz2,D⋮zN−1,DzN,D (1)
其中 X X X 表示初始种群。 L L L 和 U U U 分别表示问题解空间的下界和上界,定义了所有决策变量的可行范围: L = [ L 1 , L 2 , . . . , L D − 1 , L D ] L = [L_1, L_2, ..., L_{D-1}, L_D] L=[L1,L2,...,LD−1,LD], U = [ U 1 , U 2 , . . . , U D − 1 , U D ] U = [U_1, U_2, ..., U_{D-1}, U_D] U=[U1,U2,...,UD−1,UD]。 θ \theta θ 是一个 D 维随机向量,其中每个分量 θ d ( d = 1 , 2 , . . . , D ) \theta_d (d = 1, 2, ..., D) θd(d=1,2,...,D) 都是从均匀分布 U ( 0 , 1 ) U(0, 1) U(0,1) 中独立采样的。 ∘ \circ ∘ 表示哈达玛积(逐元素乘法)。
创建初始种群后,目标函数 f ( ⋅ ) f(\cdot) f(⋅) 评估种群的适应度。然后选择并标记适应度值最高的三个个体为 k 1 k_1 k1、 k 2 k_2 k2 和 k 3 k_3 k3。
2.2. 收敛方程的设计
AOM 之后,各种势力中出现了三个最强大的力量,形成了魏、蜀汉和东吴三个国家。这三个国家并非完全对立。它们之间也存在一定程度的合作。当其中一个国家变得足够强大并对另外两个国家构成威胁时,较弱的国家会联合起来对抗最强大的国家,进入 JC 阶段。当三个国家的实力达到平衡状态,即没有任何一个国家能够消灭其他两国时,它们倾向于独立发展,吸引更多力量以增强实力,从而进入 TLT 阶段。随着时间的推移,随着三个国家的实力逐渐增强,联合抵抗的可能性降低,导致每个国家都倾向于独立发展。
这个过程类比了三国时期的联合抵抗和权力平衡的历史阶段。在元启发式算法的优化过程中,算法的全局探索能力和局部开发能力表现出既冲突又互补的关系。元启发式算法的搜索过程始于对整个解空间的广泛探索,以识别寻找全局最优的潜在区域,然后密集地开发这些区域以提高解的质量。全局探索和局部开发之间的平衡对算法性能至关重要。重要的是,在进行局部开发的同时,仍需保持一定的全局探索概率,以避免陷入局部最优。这种探索概率在整个过程中动态衰减,逐步将计算资源重新分配到优化最优解上,从而提高整体优化效果。
在 KING 中,JC 和 TLT 阶段分别主要履行全局探索和局部开发的核心功能。一个动态的权衡因子 (TF) 自适应地将每个搜索代理引导到由探索或开发阶段生成的解向量,从而实现探索与开发之间的平衡。这个关键的选择机制由公式 (2) 控制:
x i t + 1 = { j x i , If r 1 > T F t x i , Otherwise (2) x_{i}^{t+1} = \begin{cases} jx_i, & \text{If } r_1 > TF \\ tx_i, & \text{Otherwise} \end{cases} \tag{2} xit+1={jxi,txi,If r1>TFOtherwise(2)
具体来说, x i t + 1 x_i^{t+1} xit+1 表示在第 t t t 次迭代中,种群内与第 i i i 个个体 x i x_i xi 对应的代理个体。 j x i jx_i jxi 的选择是通过比较 TF 值与一个在 0 和 1 之间均匀分布的随机数 r 1 r_1 r1 来决定的。 j x i jx_i jxi 和 t x i tx_i txi 分别表示通过全局探索(JC)和局部开发(TLT)阶段计算出的解向量。TF 的计算如公式 (3) 所示:
T F = tanh ( π × ( r 2 − 0.5 ) ) h MaxFEs (3) TF = \tanh \left( \pi \times \left( r_2 - 0.5 \right) \right)^{\frac{h}{\text{MaxFEs}}} \tag{3} TF=tanh(π×(r2−0.5))MaxFEsh(3)
tanh ( ⋅ ) \tanh(\cdot) tanh(⋅) 函数关于 r = 0.5 r = 0.5 r=0.5 对称,实现了探索和开发概率之间的平滑过渡。在 ( 0 , 1 ) (0,1) (0,1) 内均匀分布的随机数 r 2 r_2 r2 为个体选择引入了不确定性。当 r 2 > 0.5 r_2 > 0.5 r2>0.5 时, tanh ( π × ( r 2 − 0.5 ) ) > 0 \tanh(\pi \times (r_2 - 0.5)) > 0 tanh(π×(r2−0.5))>0,导致指数项减小,TF 值增大,从而增强了局部开发的趋势。当 r 2 < 0.5 r_2 < 0.5 r2<0.5 时,指数项增大,TF 值减小,增强了全局探索的趋势。 MaxFEs \text{MaxFEs} MaxFEs 表示最大函数评估次数。将其包含在分母中限制了指数的大小,防止 TF 在优化后期对随机扰动过度敏感。参数 h h h 模拟优化过程和历史演化类比的进展,定义如公式 (4):
h = FEs MaxFEs (4) h = \sqrt{\frac{\text{FEs}}{\text{MaxFEs}}} \tag{4} h=MaxFEsFEs (4)
平方根函数确保早期优化阶段的探索速率显著快于后期阶段的开发速率,这与自然优化过程中观察到的指数衰减模式一致。 FEs \text{FEs} FEs 表示当前的函数评估次数。
- 初始阶段 ( FEs = 1 \text{FEs} = 1 FEs=1) : h → 0 ⟹ T F → 0 h \to 0 \implies TF \to 0 h→0⟹TF→0,全局探索主导早期优化阶段。
- 中间阶段 ( FEs = 0.5 × MaxFEs \text{FEs} = 0.5 \times \text{MaxFEs} FEs=0.5×MaxFEs) : h ≈ 0.707 ⟹ T F h \approx 0.707 \implies TF h≈0.707⟹TF 逐渐增加,标志着向局部开发的过渡。
- 收敛阶段 ( FEs → MaxFEs \text{FEs} \to \text{MaxFEs} FEs→MaxFEs) : h → 1 ⟹ T F → 1 h \to 1 \implies TF \to 1 h→1⟹TF→1,局部开发主导最终收敛阶段。
通过 TF 和历史进展参数 h h h 的协同设计,KING 算法根据优化进度动态调节 JC 和 TLT 阶段的激活概率。这实现了全局探索和局部开发之间的自适应平衡,无需预定义阶段切换阈值。
2.2.1. 全局探索:联合对抗 (JC)
JC 阶段模拟了三国时期的历史场景,即较弱的国家结成联盟以对抗主导势力。当三个国家中的一个变得足够强大,对另外两个构成威胁时,较弱的国家联合起来对抗当前最强大的国家,启动 JC 阶段。在此阶段,两个较弱的国家 k 2 k_2 k2 和 k 3 k_3 k3 共享特定的实力组成部分,形成一个联合力量 j x i jx_i jxi 以对抗主导国家 k 1 k_1 k1。JC 解向量 j x i jx_i jxi 的第 j j j 个分量 j x i , j jx_{i,j} jxi,j 由公式 (5) 定义:
j x i , j = w × T k 2 , j + ( 1 − w ) × T k 3 , j (5) jx_{i,j} = w \times Tk_{2,j} + (1 - w) \times Tk_{3,j} \tag{5} jxi,j=w×Tk2,j+(1−w)×Tk3,j(5)
w w w 是 ( 0 , 1 ) (0,1) (0,1) 内均匀分布的随机数, w ∼ U ( 0 , 1 ) w \sim U(0,1) w∼U(0,1),控制着来自两个次优个体 T k 2 , j Tk_{2,j} Tk2,j 和 T k 3 , j Tk_{3,j} Tk3,j 修正项的混合比例。通过混合 T k 2 , j Tk_{2,j} Tk2,j 和 T k 3 , j Tk_{3,j} Tk3,j, j x i , j ∈ [ min ( T k 2 , j , T k 3 , j ) , max ( T k 2 , j , T k 3 , j ) ] jx_{i,j} \in [\min(Tk_{2,j}, Tk_{3,j}), \max(Tk_{2,j}, Tk_{3,j})] jxi,j∈[min(Tk2,j,Tk3,j),max(Tk2,j,Tk3,j)]。这保证了 j x i , j jx_{i,j} jxi,j 位于由两个次优修正项定义的高质量区域内,从而有利于继承有益的历史优化经验。修正项 T k 2 , j Tk_{2,j} Tk2,j 和 T k 3 , j Tk_{3,j} Tk3,j 通过公式 (6) 和 (7) 计算:
T k 2 , j = w 1 × k 2 , j + ( 1 − w 1 ) × x i , j + r 3 × ( r 4 × ( U j − L j ) + L j ) (6) Tk_{2,j} = w_1 \times k_{2,j} + (1 - w_1) \times x_{i,j} + r_3 \times (r_4 \times (U_j - L_j) + L_j) \tag{6} Tk2,j=w1×k2,j+(1−w1)×xi,j+r3×(r4×(Uj−Lj)+Lj)(6)
T k 3 , j = w 2 × k 3 , j + ( 1 − w 2 ) × x i , j + r 5 × ( r 6 × ( U j − L j ) + L j ) (7) Tk_{3,j} = w_2 \times k_{3,j} + (1 - w_2) \times x_{i,j} + r_5 \times (r_6 \times (U_j - L_j) + L_j) \tag{7} Tk3,j=w2×k3,j+(1−w2)×xi,j+r5×(r6×(Uj−Lj)+Lj)(7)
T k 2 , j Tk_{2,j} Tk2,j 和 T k 3 , j Tk_{3,j} Tk3,j 将当前个体与一个次优精英个体混合,并加入全局随机扰动。 w 1 , w 2 , r 3 , r 4 , r 5 , r 6 ∼ U ( 0 , 1 ) w_1, w_2, r_3, r_4, r_5, r_6 \sim U(0,1) w1,w2,r3,r4,r5,r6∼U(0,1) 是独立生成的。 w 1 w_1 w1 和 w 2 w_2 w2 调节精英个体分量的保留强度。 k 2 , j k_{2,j} k2,j 和 k 3 , j k_{3,j} k3,j 分别表示两个次优个体 k 2 k_2 k2 和 k 3 k_3 k3 的第 j j j 个分量。 x i , j x_{i,j} xi,j 表示当前个体 x i x_i xi 的第 j j j 个分量。扰动项在第 j j j 维的整个可行范围 [ L j , U j ] [L_j, U_j] [Lj,Uj] 内生成一个均匀分布的步长。这赋予 j x i jx_i jxi 在整个解空间进行随机跳跃的能力。
JC 作为一种全局探索策略。它通过将当前个体与次优精英个体混合来操作,利用了与有希望的收敛方向相关的信息。同时,它引入了由解空间限制界定的随机幅度的探索步长。这种机制显著降低了算法陷入局部最优的风险,并促进了解空间的全面全局搜索。
2.2.2. 局部开发:三足鼎立 (TLT)
TLT 阶段模拟了三国时期三个国家追求独立发展的历史时期。当它们的实力达到均衡状态,以至于没有任何一个国家能够消灭其他两国时,它们倾向于专注于自主发展,吸引周边势力以增强各自的实力。在此发展过程中,每个国家 k 1 k_1 k1、 k 2 k_2 k2、 k 3 k_3 k3 通过弥补弱点 P t 1 Pt_1 Pt1 和放大优势 P t 2 Pt_2 Pt2 来增强其实力。个体 x i x_i xi 的 TLT 解向量 t x i tx_i txi 由公式 (8) 定义:
t x i = b x + ( P t 1 + P t 2 ) ∘ L ( D ) (8) tx_i = bx + (Pt_1 + Pt_2) \circ L(D) \tag{8} txi=bx+(Pt1+Pt2)∘L(D)(8)
其中:
b x = { x n 1 , If f ( x n 1 ) < f ( x i ) x i , Otherwise n 1 ∈ { 1 , 2 , . . . , N } , n 1 ≠ i bx = \begin{cases} x_{n1}, & \text{If } f(x_{n1}) < f(x_i) \\ x_i, & \text{Otherwise} \end{cases} \quad n1 \in \{1,2,...,N\}, \quad n1 \neq i bx={xn1,xi,If f(xn1)<f(xi)Otherwisen1∈{1,2,...,N},n1=i
b x bx bx 表示当前个体 x i x_i xi 或从种群中随机选择的、具有更优适应度值的个体 x n 1 x_{n1} xn1。索引 n 1 n1 n1 是从排除 i i i 的种群索引中随机选择的。如果 f ( x n 1 ) < f ( x i ) f(x_{n1}) < f(x_i) f(xn1)<f(xi),则选择随机精英 x n 1 x_{n1} xn1 以提升开发质量。如果 f ( x n 1 ) ≥ f ( x i ) f(x_{n1}) \ge f(x_i) f(xn1)≥f(xi),则保留当前解 x i x_i xi 以维持种群多样性。这种随机精英选择促进了多样化的开发轨迹,减轻了单一精英引导策略相关的早熟收敛风险。开发增强项 P t 1 Pt_1 Pt1 和 P t 2 Pt_2 Pt2 通过公式 (9) 和 (10) 计算。 L ( D ) L(D) L(D) 是一个 D 维向量,其每个分量都遵循 Lévy 分布 [43]。与均匀随机分布相比,Lévy 分布主要生成小步长,确保高精度的局部开发,同时具有重尾特性,偶尔会产生大步长,有助于算法逃离局部最优。
P t 1 = δ 1 ∘ ( x n 2 − b x ) (9) Pt_1 = \delta_1 \circ (x_{n2} - bx) \tag{9} Pt1=δ1∘(xn2−bx)(9)
P t 2 = δ 2 ∘ ( b x − x i ) (10) Pt_2 = \delta_2 \circ (bx - x_i) \tag{10} Pt2=δ2∘(bx−xi)(10)
δ 1 \delta_1 δ1 和 δ 2 \delta_2 δ2 是 D 维随机向量,其分量均匀分布, δ 1 , δ 2 ∼ U D ( 0 , 1 ) \delta_1, \delta_2 \sim U_D(0,1) δ1,δ2∼UD(0,1)。 n 2 n2 n2 是随机选择的精英索引, n 2 ∼ U { 1 , 2 , 3 } n2 \sim U\{1,2,3\} n2∼U{1,2,3}。 P t 1 Pt_1 Pt1 构建一个由随机选择的精英个体 x n 2 x_{n2} xn2 引导的探索步长,促进精英引导的开发。 P t 2 Pt_2 Pt2 仅在 b x = x n 1 bx = x_{n1} bx=xn1(即选择了随机精英)时激活。它过滤掉来自潜在劣质解 x i x_i xi 的信息,有助于加速收敛。
TLT 采用一个基个体 b x bx bx,选择为当前解或随机选择的具有更好适应度的解。该策略在保持多样性的同时提高了种群质量。基于 Lévy 分布的随机步长和来自相对更优解的信息的引入,使算法能够围绕基个体 b x bx bx 确定的潜在区域提高解的精度,同时通过 Lévy 飞行固有的长跳提供逃离局部最优的机会。
2.2.3. 增强收敛:全国统一 (WCU)
WCU 阶段模拟了最强大的国家逐渐同化其他国家的进程。在 WCU 期间,三个国家之间实力发展的差距日益增大,使得两个较弱国家 k 2 k_2 k2 和 k 3 k_3 k3 的联盟在对抗主导国家 k 1 k_1 k1 时效果逐渐减弱。因此,最强大的国家逐渐吞并剩余的实体 x i , j x_{i,j} xi,j,建立统一的主权。该主权通过评估所有势力的实力组成部分来协调全球发展,以促进均衡发展。WCU 解向量 w x i wx_i wxi 的第 j j j 个分量 w x i , j wx_{i,j} wxi,j 通过公式 (11) 构建:
w x i , j = { c x i , j , If r 7 > p i x i , j , Otherwise (11) wx_{i,j} = \begin{cases} cx_{i,j}, & \text{If } r_7 > p_i \\ x_{i,j}, & \text{Otherwise} \end{cases} \tag{11} wxi,j={cxi,j,xi,j,If r7>piOtherwise(11)
w x i , j wx_{i,j} wxi,j 由协调调度参数 p i p_i pi 决定,选择要么保留原始个体 x i , j x_{i,j} xi,j,要么构建相应的解向量 c x i , j cx_{i,j} cxi,j。这里, r 7 ∼ U ( 0 , 1 ) r_7 \sim U(0,1) r7∼U(0,1) 是一个均匀分布的随机数。参数 p i p_i pi 是一个个体评估度量,源自所有个体归一化适应度值的函数:
p i = 1 v sech 2 ( m i ) (12) p_i = \frac{1}{v} \operatorname{sech}^2 (m_i) \tag{12} pi=v1sech2(mi)(12)
其中 m i m_i mi 定义为:
m i = { 0 , If d max = d min d i − d min d max − d min , Otherwise (13) m_i = \begin{cases} 0, & \text{If } d_{\max} = d_{\min} \\ \frac{d_i - d_{\min}}{d_{\max} - d_{\min}}, & \text{Otherwise} \end{cases} \tag{13} mi={0,dmax−dmindi−dmin,If dmax=dminOtherwise(13)
d i = ∣ f i − f best ∣ d_i = |f_i - f_{\text{best}}| di=∣fi−fbest∣
v = 2 v = 2 v=2 是一个控制概率分布 p p p 范围的缩放因子。该参数的敏感性在第 5.3 节中分析。 sech ( ⋅ ) \operatorname{sech}(\cdot) sech(⋅) 表示双曲正割函数,对归一化偏差执行非线性变换。这个偶函数在整个实数域上表现出对称、单调递减的行为,在 m = 0 m = 0 m=0 时达到最大值 1,并随着 m → ± ∞ m \to \pm \infty m→±∞ 渐近趋近于 0。 m i m_i mi 表示种群内的归一化适应度偏差,量化了个体 i i i 的质量差距。 d i = ∣ f i − f best ∣ d_i = |f_i - f_{\text{best}}| di=∣fi−fbest∣ 是当前个体 f i f_i fi 和当前最优个体 f best f_{\text{best}} fbest 之间适应度的绝对差值。 d max d_{\max} dmax 和 d min d_{\min} dmin 分别是整个种群中 d i d_i di 的最大值和最小值。
通过归一化,适应度偏差被映射到区间 [ 0 , 1 ] [0,1] [0,1]。适应度较差的个体表现出较大的 m i m_i mi 值。经过 sech ( ⋅ ) \operatorname{sech}(\cdot) sech(⋅) 的非线性平滑后,这些个体产生较小的 p i p_i pi 值,从而为构建 c x i , j cx_{i,j} cxi,j 赋予了更高的概率。分量 c x i , j cx_{i,j} cxi,j 通过融入当前最优个体来提高解精度,并通过公式 (14) 计算:
c x i , j = h × best j + ( 1 − h ) × x i , j + r 8 × ( best j − x i , j ) (14) cx_{i,j} = h \times \text{best}j + (1 - h) \times x{i,j} + r_8 \times (\text{best}j - x{i,j}) \tag{14} cxi,j=h×bestj+(1−h)×xi,j+r8×(bestj−xi,j)(14)
c x i , j cx_{i,j} cxi,j 将当前个体 x i , j x_{i,j} xi,j 与当前最优个体 best j \text{best}_j bestj 的对应维度分量混合,并加入随机扰动。 h h h 是模拟优化过程和三国历史演化的历史进展参数,先前在公式 (4) 中定义。在 WCU 中, h h h 控制当前个体和最优个体之间的混合比例。随着优化进程的推进, h h h 增加,逐步放大最优个体的影响以加速收敛。 r 8 ∼ U ( 0 , 1 ) r_8 \sim U(0,1) r8∼U(0,1) 是一个控制局部探索步长幅度的随机数。
在种群更新期间,下一代个体 x i t + 1 x_i^{t+1} xit+1 是通过在原始个体 x i x_i xi 和 WCU 解向量 w x i wx_i wxi 之间贪婪地选择最佳解来确定的。对于最小化问题,KING 的种群更新定义如公式 (15):
x i t + 1 = { w x i , If f ( w x i ) < f ( x i ) x i , Otherwise (15) x_i^{t+1} = \begin{cases} wx_i, & \text{If } f(wx_i) < f(x_i) \\ x_i, & \text{Otherwise} \end{cases} \tag{15} xit+1={wxi,xi,If f(wxi)<f(xi)Otherwise(15)
WCU 阶段通过归一化适应度评估选择质量较低的目标个体。它通过将这些目标个体与当前最优解混合来提高解精度。此外,在整个优化过程中逐渐增强的最优解影响力确保了算法的高效收敛。
2.3. 约束处理方法:等式约束的动态容差
通过包含等式约束和不等式约束的聚合约束违反度量来评估解的可行性,如公式 (16)、(17)、(18) 所形式化。对于一个具有 p p p 个不等式约束 g ( x ) g(x) g(x) 和 m m m 个等式约束 h ( x ) h(x) h(x) 的优化问题。令 s v c x , ϵ t svc_{x,\epsilon_t} svcx,ϵt 表示在等式容差 ϵ t \epsilon_t ϵt 下解 x x x 的总约束违反。 I ( x ) I(x) I(x) 表示累积不等式约束违反, E x , ϵ t E_{x,\epsilon_t} Ex,ϵt 表示在容差 ϵ t \epsilon_t ϵt 下的累积等式约束违反。违反度量计算如下:
s v c x , ϵ t = I ( x ) + E x , ϵ t (16) svc_{x,\epsilon_t} = I(x) + E_{x,\epsilon_t} \tag{16} svcx,ϵt=I(x)+Ex,ϵt(16)
I ( x ) = ∑ i = 1 p max ( g i ( x ) , 0 ) (17) I(x) = \sum_{i=1}^{p} \max(g_i(x), 0) \tag{17} I(x)=i=1∑pmax(gi(x),0)(17)
E x , ϵ t = ∑ j = 1 m max ( ∣ h j ( x ) ∣ − ϵ t , 0 ) (18) E_{x,\epsilon_t} = \sum_{j=1}^{m} \max(|h_j(x)| - \epsilon_t, 0) \tag{18} Ex,ϵt=j=1∑mmax(∣hj(x)∣−ϵt,0)(18)
每个等式约束 h j ( x ) h_j(x) hj(x) 的容差参数 ϵ j , t \epsilon_{j,t} ϵj,t 通过公式 (19) 动态调整。
ϵ j , t = { max ( ϵ f × t FEs c , ϵ f ) , If FEs < FEs c and x i is ϵ − feasible ϵ f , Other case (19) \epsilon_{j,t} = \begin{cases} \max \left( \frac{\epsilon_f \times t}{\text{FEs}_c}, \epsilon_f \right), & \text{If FEs} < \text{FEs}_c \text{ and } x_i \text{ is } \epsilon - \text{feasible} \\ \epsilon_f, & \text{Other case} \end{cases} \tag{19} ϵj,t={max(FEscϵf×t,ϵf),ϵf,If FEs<FEsc and xi is ϵ−feasibleOther case(19)
其中 ϵ f \epsilon_f ϵf 表示最终容差阈值。 ϵ − feasible \epsilon - \text{feasible} ϵ−feasible 条件要求等式约束违反为零( E x i , ϵ j , t = 0 E_{x_i,\epsilon_{j,t}} = 0 Exi,ϵj,t=0)且 ϵ j , t > ϵ f \epsilon_{j,t} > \epsilon_f ϵj,t>ϵf。容差调整在预定义的最大评估预算 FEs c \text{FEs}_c FEsc 内进行。
对于最小化问题,候选解 u i u_i ui 和父代 x i x_i xi 之间的更新遵循公式 (20) 中的分层选择规则。选择优先级首先考虑较低的约束违反幅度。当两个解都可行时,选择具有更优适应度值的个体。这种双阶段机制通过约束违反优先排序确保严格的可行性执行,并在可行条件下进行最优解精炼。
x i t + 1 = { u i , If s v c u i , ϵ t < s v c x i , ϵ t x i , Other case (20) x_i^{t+1} = \begin{cases} u_i, & \text{If } svc_{u_i,\epsilon_t} < svc_{x_i,\epsilon_t} \\ x_i, & \text{Other case} \end{cases} \tag{20} xit+1={ui,xi,If svcui,ϵt<svcxi,ϵtOther case(20)
越界解通过公式 (21) 重新配置。
x i , j = { U j − r 9 × ( U j − L j ) , If x i , j > U j L j + r 9 × ( U j − L j ) , If x i , j < L j (21) x_{i,j} = \begin{cases} U_j - r_9 \times (U_j - L_j), & \text{If } x_{i,j} > U_j \\ L_j + r_9 \times (U_j - L_j), & \text{If } x_{i,j} < L_j \end{cases} \tag{21} xi,j={Uj−r9×(Uj−Lj),Lj+r9×(Uj−Lj),If xi,j>UjIf xi,j<Lj(21)
其中 U j U_j Uj 和 L j L_j Lj 表示第 j j j 个决策变量的上/下界, r 9 ∈ ( 0 , 0.1 ) r_9 \in (0,0.1) r9∈(0,0.1) 作为随机缩放因子。
2.4. KING 在约束优化中的实现
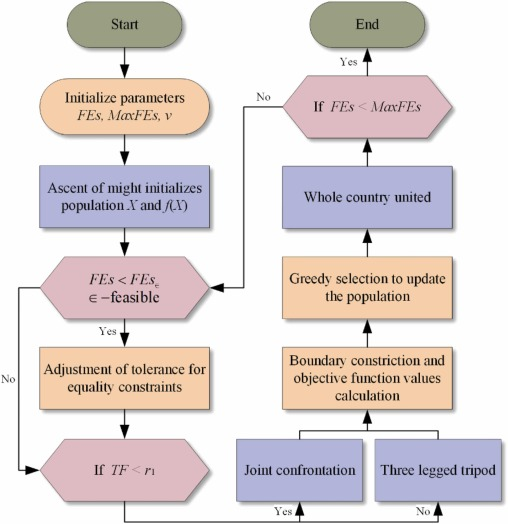
AOM 为 KING 初始化种群及其目标函数值之后。首先,在 FEs < FEs c \text{FEs} < \text{FEs}_c FEs<FEsc 且 ϵ − feasible \epsilon - \text{feasible} ϵ−feasible 的条件下,动态调整个体对等式约束的容差。随后,使用权衡因子 TF 来决定是使用 JC 还是 TLT 来更新种群的解向量。在此过程中,解向量存在越界的风险,因此,在计算目标函数值之前必须对种群进行边界处理。接下来,使用贪婪选择方法更新种群。最后,使用 WCU 来引导算法收敛,实现探索策略与开发策略之间的平衡。WCU 包含解向量更新、边界处理、目标函数值评估和种群更新的完整过程。综上所述,KING 的流程图如图 3 所示。
Dong Zhao, Zhen Wang, Yupeng Li, Ali Asghar Heidari, Zongda Wu, Yi Chen, Huiling Chen, KING: An efficient optimization approach, Neurocomputing, Volume 657, 2025, 131645, https://doi.org/10.1016/j.neucom.2025.131645. .