在前面几篇文章中，我们谈了SVD的基本原理，从几何角度用二维坐标展示了SVD的拉伸和旋转。现在通过一张具体的图片来看看SVD是如何处理矩阵的。
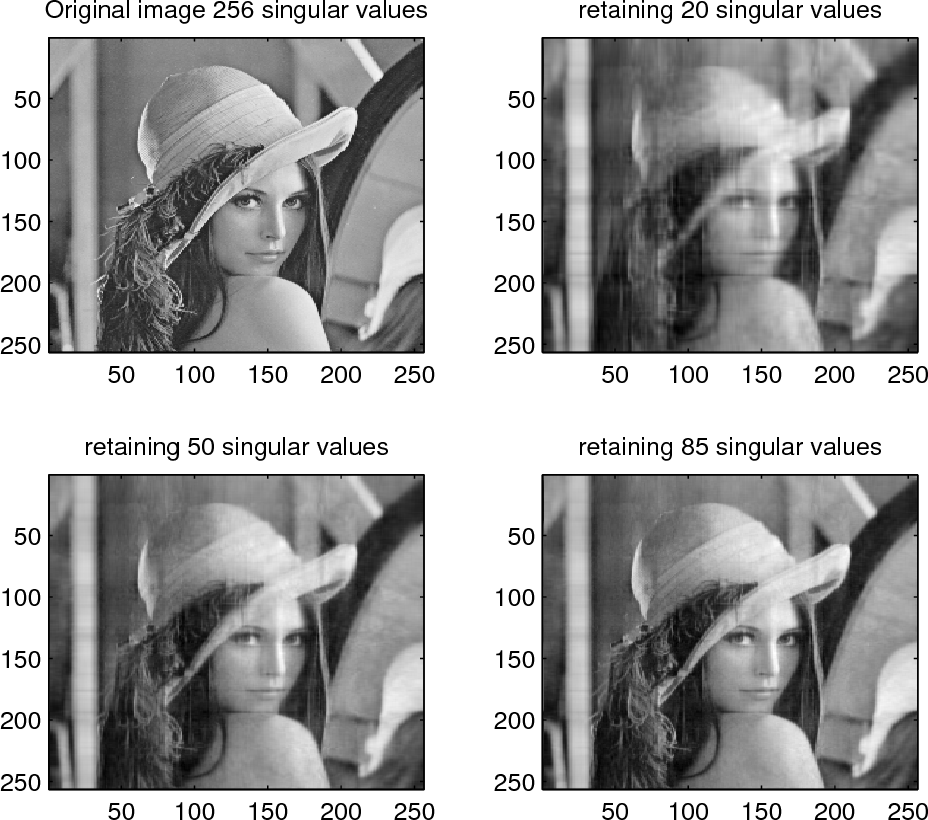
下图展示的是：把一张 256×256 的灰度图当成一个矩阵 A，做 SVD 分解后，只保留前 k 个奇异值（以及对应的左右奇异向量），就能得到一张"压缩/降噪后的近似图"。
图片分析
这张图片是一个2x2的网格图，展示了同一张灰度图像（一位戴帽子的女性侧脸照）在不同奇异值保留数量下的效果，演示了奇异值分解（SVD）在图像压缩中的应用。图像尺寸看起来是256x256像素（基于坐标轴从50到250，步长50），原图有256个奇异值（这在方阵图像中常见，因为最小维度决定最大奇异值数量）。
- 左上：Original Image 256 singular values 这是原始图像，细节清晰，包括女性的头发卷曲、帽子纹理、眼睛和面部表情都锐利可见。没有压缩，保留所有奇异值，因此图像质量最高，但数据量最大。
- 右上：retaining 20 singular values 只保留前20个最大的奇异值，图像严重模糊，几乎看不清细节，只有大致轮廓（如帽子形状和脸部大体位置）。这展示了低秩近似导致的信息丢失，适合极致压缩但牺牲质量。
- 左下：retaining 50 singular values 保留前50个奇异值，图像清晰度有所改善，能辨认出头发、眼睛和帽子的基本结构，但仍有噪点和模糊，细节如羽毛纹理不清晰。这是一个中等压缩水平，平衡了文件大小和可读性。
- 右下：retaining 85 singular values 保留前85个奇异值，图像质量进一步提升，几乎接近原图，能清楚看到面部表情、头发细节和帽子边缘。只有细微的模糊或噪点，这表明85个奇异值已捕捉到大部分图像信息，压缩效率高。
总体来说，随着保留奇异值数量增加，图像从模糊到清晰过渡，证明SVD可以有效压缩图像而保留主要特征。原图可能是一个经典的测试图像（如Lena图像的变体），用于展示低秩逼近的效果。压缩率可以粗略估计：对于256x256图像，原数据量约65KB（假设8-bit灰度）；保留k个奇异值时，存储需求约为k(256+256+1)（U的k列、V的k行、Σ的k值），例如k=20时压缩到约10%大小。
1) 图像为什么能做 SVD？
灰度图可以看成矩阵：
-
行 = 垂直方向的像素位置
-
列 = 水平方向的像素位置
-
矩阵元素
= 像素灰度值（0~255）
SVD 把它分解成：
其中：
-
U：一组"纵向模式"（256 个长度为 256 的正交向量）
-
V：一组"横向模式"
-
Σ：对角线上的奇异值
更直观的写法是"很多张 rank-1 图的叠加"：
每一项 都像一张"基础纹理/阴影层"，把它们加起来就还原原图。
2) 为什么"只保留前 k 个"会得到模糊但像的图？
保留前 k 个就是：
性质很关键：这是所有 rank-k 矩阵里，对原图误差最小的近似（Eckart--Young 定理）。
直觉：
-
大的奇异值通常对应"整体结构"：脸的轮廓、明暗大块、帽子形状等低频信息
-
小的奇异值更像"细节与高频"：发丝、边缘锐利变化、纹理噪声等
所以：
-
k 小 ⇒ 只剩大结构 ⇒ 更平滑、更糊
-
k 大 ⇒ 细节回来 ⇒ 更接近原图
3) 读图：20 / 50 / 85 的区别在说什么？
你图里四张：
-
Original image 256 singular values
用了全部 256 个奇异值（理论上可完整重建原图）。
-
retaining 20 singular values
只用 20 个"最重要层"。你会看到：主体还在，但明显糊，细节几乎没了，还会出现一些"条带/块状"的感觉------这是因为只用少量 rank-1 外积叠加，表达能力有限。
-
retaining 50 singular values
轮廓更稳，五官更清楚一些，但纹理仍弱。
-
retaining 85 singular values
已经相当像原图了，边缘和头发细节明显恢复。
4) 这为什么能"压缩"？
原图需要存 256×256=65536 个数。
如果只保留 k 个奇异值，需要存：
-
-
-
总量约：
举例（忽略额外开销与量化）：
-
k=20：513×20 = 10260（约是原来的 15.7%）
-
k=50：25650（约 39.1%）
-
k=85：43605（约 66.5%）
所以 k 越小，压缩越狠，但越糊。
实际做图像压缩还会配合：量化、整数编码、分块处理（避免全局 SVD 太贵）等。
5) SVD 在图像处理里的典型应用
A) 低秩压缩（你图展示的就是）
用较小 k 存储/传输，重建时用 。
B) 去噪（Denoising）
噪声往往更分散在"小奇异值"里：
把小的 截掉，相当于做一种"全局平滑但尽量保结构"的去噪。
C) 特征提取 / 降维（PCA 的亲戚）
把图像（或图像块）看作高维向量，SVD/ PCA 提取主成分：用于人脸识别（Eigenfaces）、检索、聚类等。
D) 背景建模/前景分离（视频里很常见）
一段视频帧堆成矩阵后，低秩部分≈稳定背景，稀疏部分≈运动前景（这思路会发展到 RPCA）。
6) 选 k 的常用办法（比"拍脑袋"更稳）
用"能量占比"选 k：
比如选到 90% / 95% 能量为止，就能在"清晰度"和"压缩率"之间做可解释的折中。
我们把这张图背后的 "每一层到底是什么" 、以及 怎么选 k、为什么会有条纹/鬼影讲透一点。
1) "保留前 k 个"到底在做什么？
SVD 给你：
-
-
-
外积
它的像素值形如 "纵向强度 × 横向强度"，所以它本质上是 一个"纵向模式"和"横向模式"相乘出来的二维图案。
-
再乘上
所以你可以把图像理解成：
很多张"非常简单的二维图案层"叠加起来，前几层负责大轮廓和大明暗，后面很多层负责细节、锐利边缘、纹理、噪声。
2) 为什么 k=20 会"糊 + 条带/鬼影"？
糊：只剩低频结构
前 20 个奇异值对应的层，通常只能很好表达：
-
大块明暗
-
平滑的阴影过渡
-
主体的大轮廓
细节（发丝、边缘锐度、细纹理）需要更多层来"拼"出来，所以被砍掉就糊。
条带/鬼影：rank-1 层的"乘法结构"太简单
单个 这层是"纵向×横向"的乘积图案，容易出现：
-
沿某些方向的条纹
-
看起来像"有一层半透明影子叠在上面"
当你只叠 20 层时，这些简化结构还没被足够多的层"互相抵消/补齐"，所以视觉上更明显。
随着 k 增大（50、85），更多层加入，结构表达能力增强，这些伪影就弱了。
3) k 越大，为什么"细节会回来"？
边缘和细纹理属于高频信息：灰度变化更快、更复杂。
表达这种复杂变化需要更多自由度，也就是需要更多的 rank-1 层去组合。
可以这样理解：
-
k 就像"用多少块乐高搭出这张图"
-
20 块：能搭出大轮廓，但细节没法搭
-
85 块：细节开始像样
-
256 块：完全复刻
4) 选 k 的更靠谱方法：看"能量占比"
常用指标：
解释： 可以看成第 i 个模式贡献的"能量"。
经验：
-
90% 能量：通常结构很清楚，但细节略软
-
95% 能量：视觉更接近原图
-
99% 能量：几乎看不出差别，但压缩优势变小
5) SVD 做压缩：到底省了多少？
原图存 256×256=65536 个数。
保留 k 个时需要存：
-
-
-
总计约 513k
所以：
-
k=20：10260（约 15.7%）
-
k=50：25650（约 39.1%）
-
k=85：43605（约 66.5%）
这就是图里"20 很糊但压缩狠，85 很清但压缩一般"的根本原因。
6) SVD 去噪：为什么"砍小奇异值"能去噪？
把噪声想成"到处乱抖的细小变化"：
-
它不太能形成强的、稳定的全局模式
-
会分散在很多小的 σi 上
所以你截断到 k：
-
保留大 σ ⇒ 保留主要结构
-
丢掉小 σ ⇒ 丢掉很多噪声成分
但注意：细节也会一起被当成"高频"砍掉，所以去噪往往伴随变糊。
7) 彩色图怎么做？
彩色图是 3 个通道（R/G/B）：
-
最简单：对每个通道分别做 SVD 截断
-
更高级：把通道联合起来做低秩模型（但实现更复杂）
我们把 SVD 的"第 i 层"单独拿出来看，你就会立刻明白为什么前 20 个像"模糊大轮廓"，后面的像"细节/噪声"。
1) 每一层是什么：一张 rank-1 的"纹理图"
对灰度图矩阵 A：
定义第 i 层（也叫第 i 个"模式/成分"）：
-
-
-
外积
所以它天然像"条带/渐变/大块阴影"，而不是复杂细节。
把前 k 层叠加就是近似图：
2) 单独看每一层时，你会看到什么（很直观）
第 1 层（最大奇异值）
通常长得像：整张图的"主光照 + 主轮廓"
-
亮暗大块很明显（类似一个"柔和的整体阴影模型"）
-
人脸/帽子/背景的主形状会隐约出现
-
非常平滑、几乎没细节
这就是为什么只保留很少的奇异值时，图还能"认得出来是谁"，但会很糊。
第 2～10 层（重要结构补充）
会开始出现：
-
更具体的轮廓强化（帽檐弧线、脸部边界）
-
某些方向性的变化（比如斜向的明暗分割）
-
仍然偏"平滑"，但结构更像原图
第 10～50 层（中频信息：纹理开始出现）
你会看到：
-
头发的成团纹理、衣服/背景的局部起伏
-
边缘更锐一些，但还不是真正"发丝级"细节
-
有时会呈现"局部条纹/波纹"样式（正常，因为 rank-1 层很像可分离的条纹组合）
第 50 之后（高频：细节 + 噪声）
越往后越像：
-
很细碎的纹理、边缘抖动
-
类似"噪点/颗粒"
-
对人眼来说贡献变小，但对"锐利感"有用
这也解释了：SVD 截断能去噪，但也会把细节一起当成"高频"砍掉。
3) 为什么你会在低 k 图里看到"鬼影/条带"？
因为你只叠加了少数几张 Ci，而每张 Ci 本身结构很"简单"（纵向×横向），容易留下方向性痕迹。
当 k 增大时，更多层加入，这些痕迹被其它层补偿/抵消，图就更自然。
4) 实际"怎么看每一层"：显示时要注意两件事
-
正负号问题（很重要）
因此你可能看到某一层是"反相"的------这是正常的。
-
幅度跨度巨大
前几层数值很大，后几层很小。要把每层显示成图，通常会对 Ci 做归一化（比如把它线性缩放到 0~255），否则后面的层几乎全黑。
5) 你可以用一个"脑内小实验"秒懂
-
把 C1 想成："拿一张很大的软毛刷，把大轮廓涂出来"
-
C2,C3... 想成："换更小的刷子补轮廓和局部阴影"
-
后面很多层："用很细的笔补发丝、颗粒、边缘锐利感"
所以只用 20 层：有大刷子、少量中刷子 → 能画出人，但细节没法画；
用到 85 层：中小刷子足够多 → 细节明显回来了。
我们继续把"为什么某些层像横/竖/斜条纹，它们到底对应图像里的什么结构"讲清楚。核心点：每个 SVD 层 是"纵向模式 × 横向模式"的乘积，所以它天然会呈现出方向性纹理。
1) 为什么会出现"横条纹 / 竖条纹"？
看一个 rank-1 层：
（把行当作 y，列当作 x）
-
如果
⇒ 整张图主要随 x 变 ⇒ 竖向条纹（因为同一列内部变化不大，列与列差别大）
-
如果
⇒ 主要随 y 变 ⇒ 横向条纹
直觉：
"谁在变化，条纹就垂直于谁的变化方向"。
2) 为什么会出现"斜条纹 / 斜向结构"？
单个 rank-1 外积本质上还是"可分离"的（x 和 y 分开），它并不能直接产生一个真正旋转的二维纹理。但你会看到"斜"的原因有两个：
原因 A：叠加效应（两层或多层合成斜向）
如果你把两张"横条纹"和"竖条纹"合在一起，或者把不同频率的条纹叠加，就能形成看起来像斜的结构（类似干涉/摩尔纹的感觉）。
也就是：
会比单独的 Ci 更"二维、更复杂"，方向感也更丰富。
原因 B：图像本身有斜向边缘
图里帽檐、头发、背景窗框等大量斜线。为了表达这些斜线，SVD 必须用很多"可分离的层"去拼，这些层在局部叠加后，就会显出斜向的增强/减弱区域，所以你视觉上会觉得"这一层像斜纹"。
3) 每一层到底"对应图像哪里"？
可以把 和
当成两个"投影权重"：
-
-
于是 生成的二维图，会在"行权重高 × 列权重高"的区域最明显------也就是这层主要在图的哪个区域"发力"。
所以：
-
前几层：
-
中间层：会开始对某些区域更敏感 ⇒ 管局部结构（比如脸、帽檐）
-
后面层：
4) "频率"这个词在这里怎么理解？
你可以把 、
想成一维信号：
-
起伏次数少 ⇒ 低频 ⇒ 对应平滑变化（大块明暗）
-
起伏次数多 ⇒ 高频 ⇒ 对应快速变化（细纹理、边缘）
越靠后的奇异向量往往越"抖"，所以对应越细的东西。
5) 为什么 SVD 压缩会"先保结构，后保细节"？
因为奇异值排序本质是在做"贡献度排序"：
-
大 σi：这一层能解释掉很多像素能量（整体误差下降最多）
-
小 σi：这一层只能修修补补（主要修细节）
所以当你只保留前 k 个时，本质是：
用最少的层，先把误差降得最多
这天然会先把"大结构"保住。
6) 一个很形象的对比：SVD vs JPEG（让你更有把握）
-
SVD（全局）：对整张图做"全局低秩"，擅长保大轮廓，代价是容易全局变糊、出现整体性伪影。
-
JPEG（分块 DCT）：把图切成 8×8 小块做频域压缩，细节保留更"局部"，但会出现块状马赛克。
所以工程上很少直接对整张大图做全局 SVD 压缩（太贵 + 伪影全局化），更常见是：
-
对小块做（类似 JPEG 思路），或
-
只把 SVD 当作去噪/降维工具，而非最终图片压缩格式。