数据结构：（一）从内存底层逻辑理解线性表

目录

[一、 绪论：重新审视"程序"的本质](#一、 绪论：重新审视“程序”的本质)

[1. 逻辑结构 vs 物理结构](#1. 逻辑结构 vs 物理结构)

[2. 时间复杂度：算法的"性价比"](#2. 时间复杂度：算法的“性价比”)

[二、 线性表之"顺序存储"：内存里的排排坐](#二、 线性表之“顺序存储”：内存里的排排坐)

[1. 原理](#1. 原理)

[2. 核心算法：插入元素 (ListInsert)](#2. 核心算法：插入元素 (ListInsert))

[三、 线性表之"链式存储"：内存里的连连看](#三、 线性表之“链式存储”：内存里的连连看)

[1. 结构](#1. 结构)

[2. 头结点（Head Node）的妙用](#2. 头结点（Head Node）的妙用)

[3. 核心算法：单链表就地逆置 (In-place Reversal)](#3. 核心算法：单链表就地逆置 (In-place Reversal))

[四、 总结与复盘：第一天必会清单](#四、 总结与复盘：第一天必会清单)

今日踩坑提醒：

---

一、 绪论：重新审视"程序"的本质

严蔚敏教授在书里强调：程序 = 算法 + 数据结构。

1. 逻辑结构 vs 物理结构

• 逻辑结构：是我们在脑子里想出来的数据关系。比如"排队"，就是线性结构。

• 物理结构（存储结构）：是数据在内存条里的真实样子。是挨着坐（顺序表），还是隔得老远靠电话线联系（链表）？

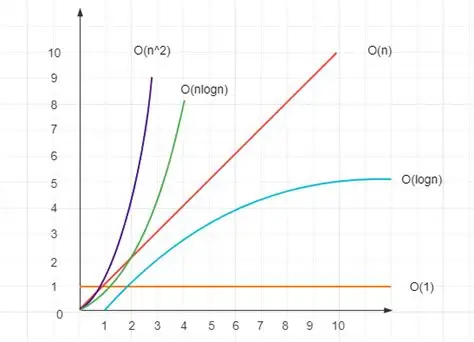
2. 时间复杂度：算法的"性价比"

面试或考试最爱问：这个算法快不快？我们用 来衡量。

• ：瞬间完成，不随数据量增加而变慢。

• ：数据多一倍，时间多一倍。

• ：高效的代名词（如二分查找）。

---

二、 线性表之"顺序存储"：内存里的排排坐

1. 原理

顺序表（SqList）本质上就是数组。它要求在内存中开辟一块连续的空间。

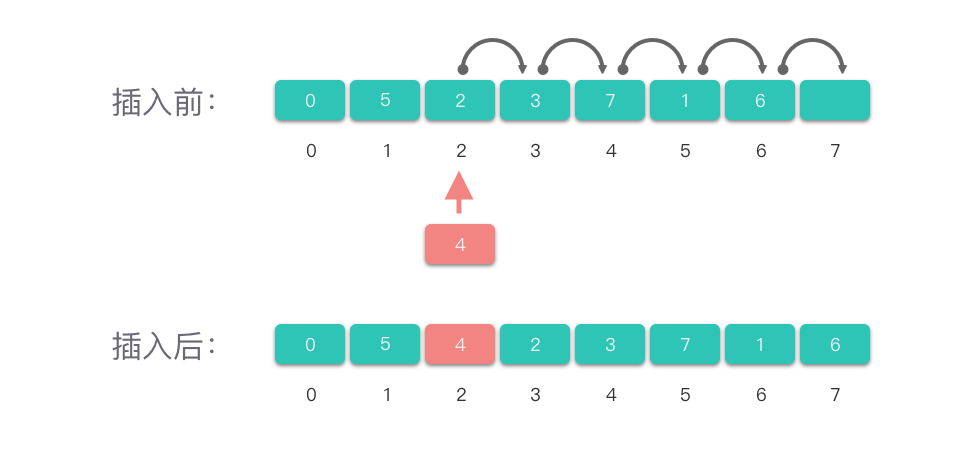
2. 核心算法：插入元素 (ListInsert)

难点注释：为什么插入时要从后往前挪？

因为如果你从前往后挪，第 个位置的值会覆盖第 个位置，导致数据丢失。

// 在第 i 个位置插入 e
for (p = &(L.elem[L.length-1]); p >= q; --p) {
    *(p+1) = *p; // 【关键】从最后一名开始，依次往后挪一个座位
}

---

三、 线性表之"链式存储"：内存里的连连看

1. 结构

链表（LinkList）由一个个节点组成。每个节点包含：数据域 (data) + 指针域 (next)。

2. 头结点（Head Node）的妙用

深度解析：教材里为什么要多弄一个不存数据的头结点？

1. 统一操作 ：如果没有头结点，在第一个位置插入节点需要修改头指针；有了它，所有位置的操作都统一为 p->next = s。

2. 空表处理 ：判断空表只需要看 L->next == NULL，非常直观。

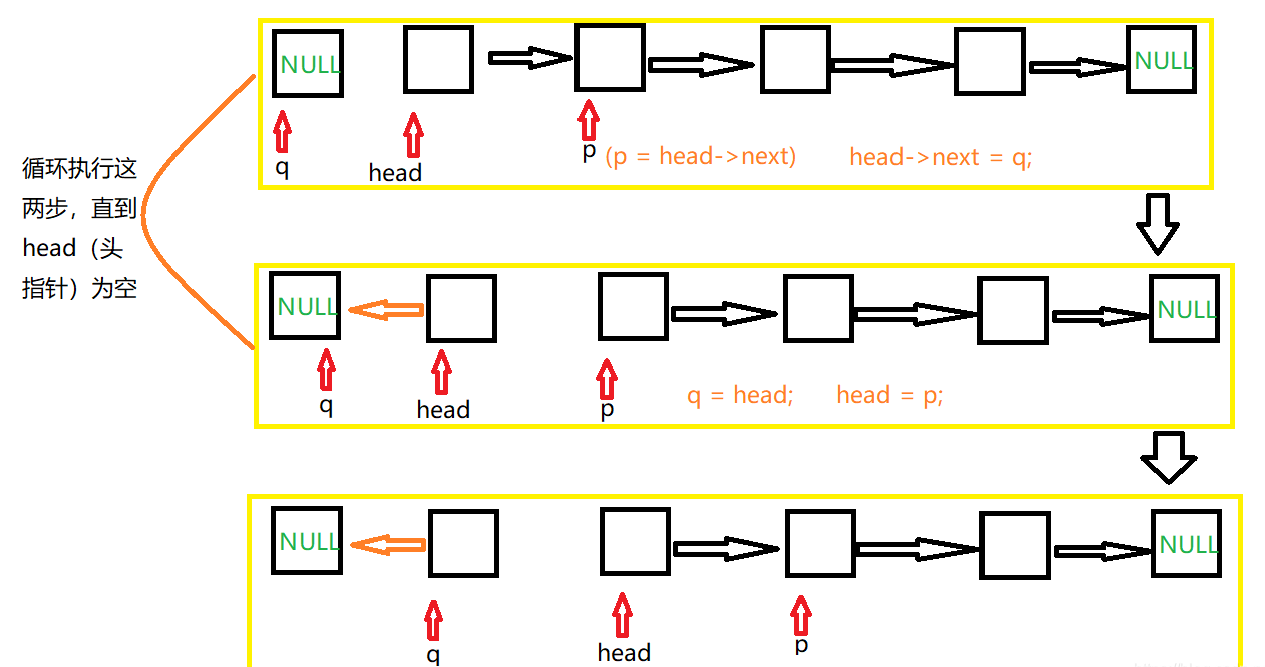
3. 核心算法：单链表就地逆置 (In-place Reversal)

这是第一天最难理解的代码。我们采用"头插法"：

// 伪代码逻辑
p = L->next;      // p 指向第一个节点
L->next = NULL;   // 把头结点砍断，当成一个空盒子
while (p) {
    q = p->next;  // 【重要】找个临时工 q 拉住后面的节点，防止断链
    p->next = L->next; // 把 p 塞进盒子里（头插法）
    L->next = p;
    p = q;        // 接手下一个待处理节点
}

---

四、 总结与复盘：第一天必会清单

维度	顺序表 (SqList)	链表 (LinkList)
空间分配	预先分配，可能浪费或溢出	动态分配，随用随申请
查找效率	(随机访问)	(得挨个找)
增删效率	(要搬家)	(改改指针就行)

今日踩坑提醒：

1. 指针越界 ：操作链表前，一定要判空 if (!p)。

2. 引用符号 & ：在 C 语言中，如果你想在函数里改变链表的结构，记得传 LinkList &L（C++语法）或者 LinkList *L（C指针）。