理论基础
来自《神经网络与深度学习》Neural Networks and Deep Learning
邱锡鹏
xpqiu@fudan.
复习下比较基础的内容,主要期待是复习一些基础概念,梯度下降、常用的损失函数、优化方法,以及循环神经网络基础,seq2seq这些,边看边记这样子,也不一定按顺序,看到哪算哪。
一、MP神经元
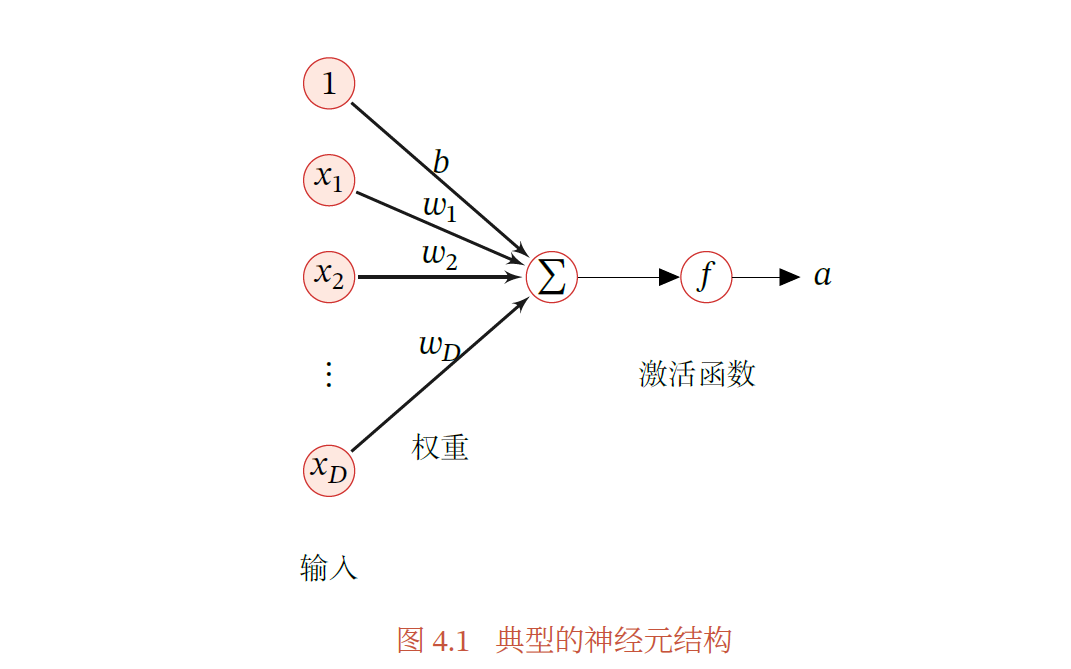
1943 年,心理学家McCulloch 和数学家Pitts 根据生物神经元的结构,提出了一种非常简单的神经元模型,MP 神经元[McCulloch et al., 1943].现代神经网络中的神经元和MP 神经元的结构并无太多变化.不同的是,MP 神经元中的激活函数𝑓 为0 或1 的阶跃函数,而现代神经元中的激活函数通常要求是连续可导的函数.

激活函数激活函数在神经元中非常重要的.为了增强网络的表示能力和学习能力,激活函数需要具备以下几点性质:
(1) 连续并可导(允许少数点上不可导)的非线性函数.可导的激活函数,可以直接利用数值优化的方法来学习网络参数.
(2) 激活函数及其导函数要尽可能的简单,有利于提高网络计算效率.
(3) 激活函数的导函数的值域要在一个合适的区间内,不能太大也不能太小,否则会影响训练的效率和稳定性.
下面介绍几种在神经网络中常用的激活函数.
激活函数
1.sigmoid型函数
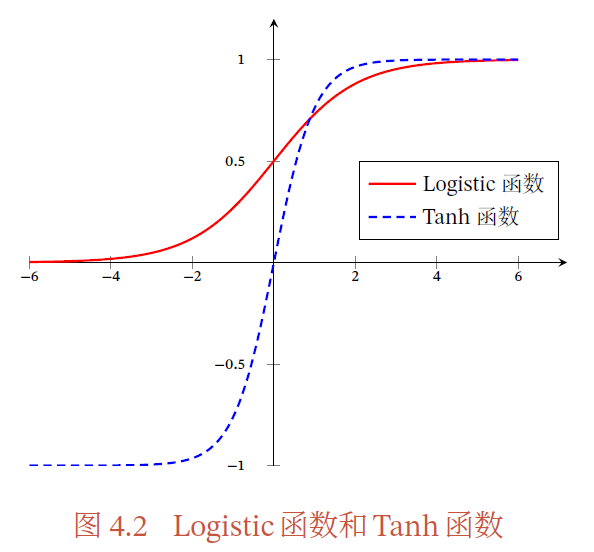
Sigmoid 型函数是指一类S 型曲线函数,为两端饱和函数.常用的Sigmoid型函数有Logistic函数和Tanh函数.

2.hard sigmoid激活函数
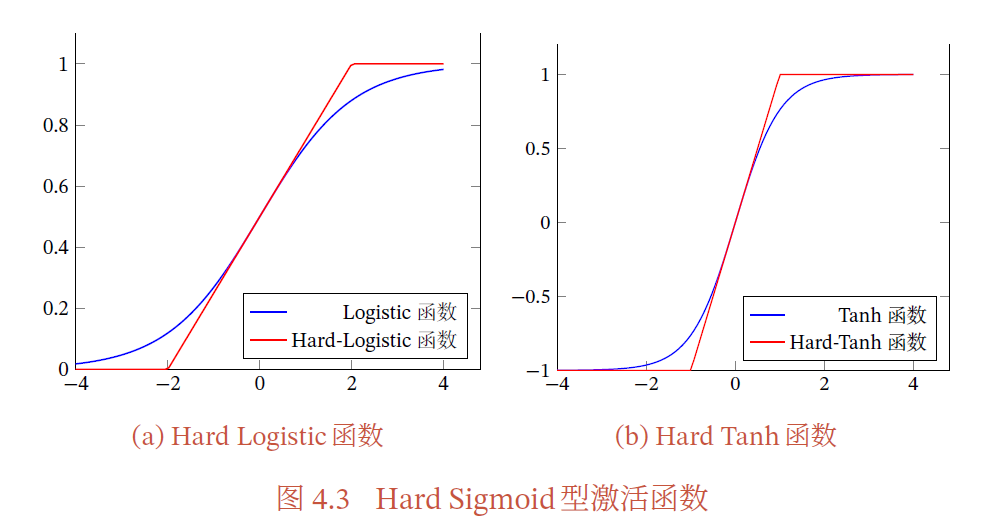
Logistic 函数和Tanh 函数都是Sigmoid 型函数,具有饱和性,但是计算开销较大 .因为这两个函数都是在中间(0 附近)近似线性,两端饱和.因此,这两个函数可以通过分段函数来近似
3.ReLU函数 系列
ReLU(Rectified Linear Unit,修正线性单元)
采用ReLU 的神经元只需要进行加、乘和比较的操作,计算上更加高效.
ReLU 函数也被认为具有生物学合理性(Biological Plausibility),比如单侧抑制、宽兴奋边界(即兴奋程度可以非常高)
在优化方面,相比于Sigmoid 型函数的两端饱和,ReLU 函数为左饱和函数,且在𝑥 > 0 时导数为1,在一定程度上缓解了神经网络的梯度消失问题,加速梯度下降的收敛速度.
ReLU 函数的输出是非零中心化的,给后一层的神经网络引入偏置偏移,会影响梯度下降的效率如果参数在一次不恰当的更新后,第一个隐藏层中的某个ReLU 神经元在所有的训练数据上都不能被激活,那么这个神经元自身参数的梯度永远都会是0,在以后的训练过程中永远不能被激活.这种现象称为死亡ReLU问题
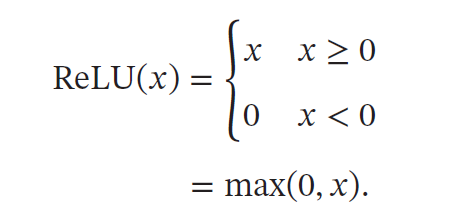
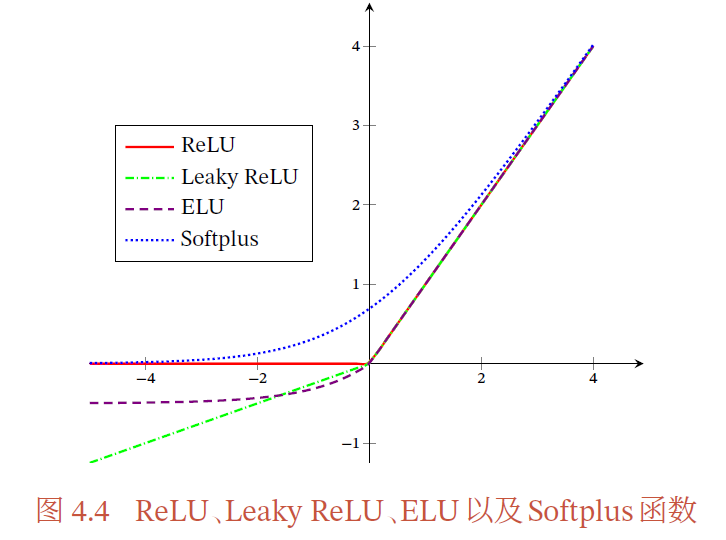
带泄露的ReLU(Leaky ReLU)在输入𝑥 < 0 时,保持一个很小的梯度𝛾.这样当神经元非激活时也能有一个非零的梯度可以更新参数,避免永远不能被激活
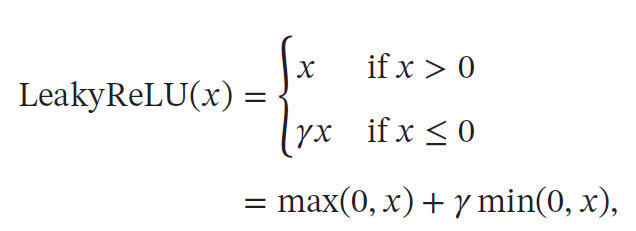
带参数的ReLU(Parametric ReLU,PReLU)引入一个可学习的参数,不同神经元可以有不同的参数
ELU(Exponential Linear Unit,指数线性单元)是一个近似的零中心化的非线性函数
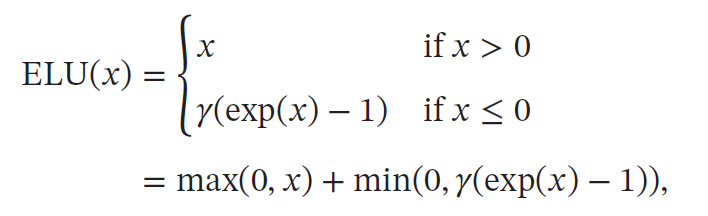
Softplus 函数可以看作ReLU函数的平滑版本
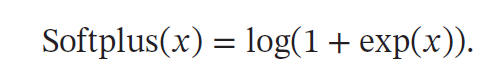
4.Swish 函数
Swish 函数是一种自门控(Self-Gated)激活函数,定义为
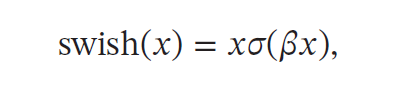
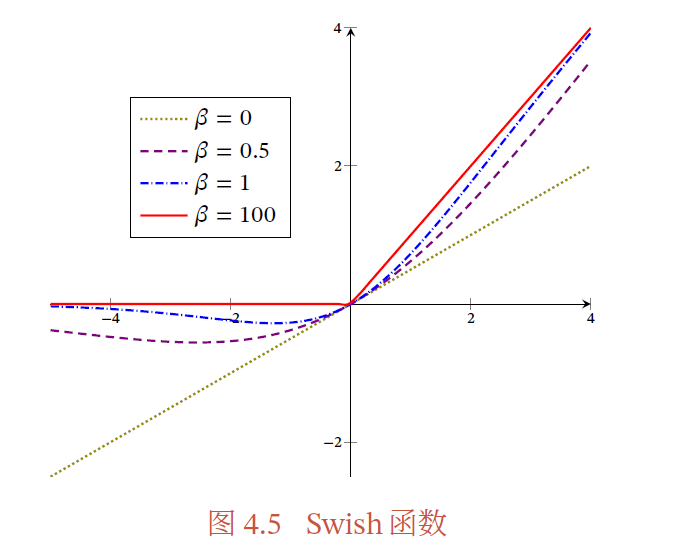
其中𝜎(⋅) 为Logistic 函数,𝛽 为可学习的参数或一个固定超参数.𝜎(⋅) ∈ (0, 1) 可以看作一种软性的门控机制.当𝜎(𝛽𝑥) 接近于1 时,门处于"开"状态,激活函数的输出近似于𝑥 本身;当𝜎(𝛽𝑥) 接近于0 时,门的状态为"关",激活函数的输出近似于0.
5.GELU 函数

6.maxout单元
是一种分段线性函数,Sigmoid 型函数、ReLU 等激活函数的输入是神经元的净输入𝑧,是一个标量.而Maxout 单元的输入是上一层神经元的全部原始输出,是一个向量𝒙 = [𝑥1; 𝑥2; ⋯ ; 𝑥𝐷].
二、前馈神经网络
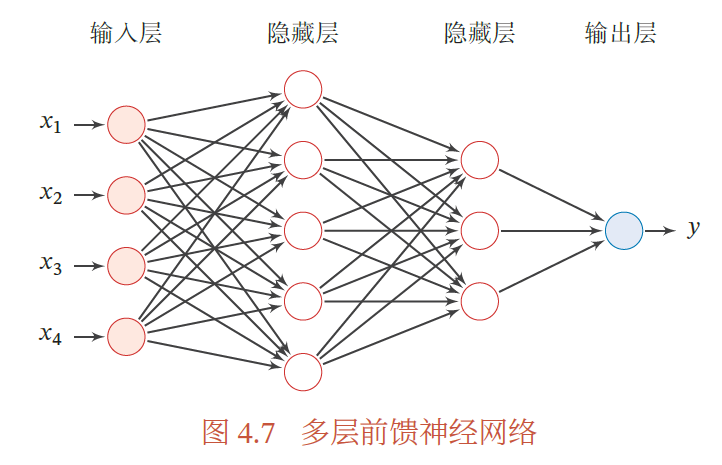
在前馈神经网络中,各神经元分别属于不同的层.每一层的神经元可以接收前一层神经元的信号,并产生信号输出到下一层.第0 层称为输入层,最后一层称为输出层,其他中间层称为隐藏层.整个网络中无反馈,信号从输入层向输出层单向传播,可用一个有向无环图表示.
三、反向传播算法
假设采用随机梯度下降进行神经网络参数学习,给定一个样本(𝒙, 𝒚),将其输入到神经网络模型中,得到网络输出为𝒚̂.假设损失函数为ℒ(𝒚, 𝒚̂),要进行参数学习就需要计算损失函数关于每个参数的导数.
 第𝑙 层的误差项可以通过第𝑙 + 1 层的误差项计算得到,这就是误差的反向传(BackPropagation,BP.反向传播算法的含义是:第𝑙 层的一个神经元的误差项(或敏感性)是所有与该神经元相连的第𝑙 + 1 层的神经元的误差项的权重和.然后,再乘上该神经元激活函数的梯度.
第𝑙 层的误差项可以通过第𝑙 + 1 层的误差项计算得到,这就是误差的反向传(BackPropagation,BP.反向传播算法的含义是:第𝑙 层的一个神经元的误差项(或敏感性)是所有与该神经元相连的第𝑙 + 1 层的神经元的误差项的权重和.然后,再乘上该神经元激活函数的梯度.
在计算出每一层的误差项之后,我们就可以得到每一层参数的梯度.因此,使用误差反向传播算法的前馈神经网络训练过程可以分为以下三步:
(1) 前馈计算每一层的净输入𝒛(𝑙) 和激活值𝒂(𝑙),直到最后一层;
(2) 反向传播计算每一层的误差项𝛿(𝑙);
(3) 计算每一层参数的偏导数,并更新参数.

自动微分与计算图
自动微分的基本原理是所有的数值计算可以分解为一些基本操作,包含+, −, ×, / 和一些初等函数exp, log, sin, cos 等,然后利用链式法则来自动计算一个复合函数的梯度.
为简单起见,这里以一个神经网络中常见的复合函数的例子来说明自动微分的过程.令复合函数𝑓(𝑥; 𝑤, 𝑏) 为
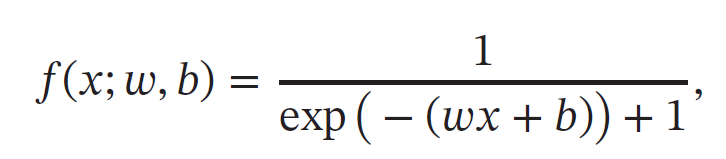
其中𝑥 为输入标量,𝑤 和𝑏 分别为权重和偏置参数.
首先,我们将复合函数𝑓(𝑥; 𝑤, 𝑏) 分解为一系列的基本操作,并构成一个计算图(Computational Graph).计算图是数学运算的图形化表示.计算图中的每个非叶子节点表示一个基本操作,每个叶子节点为一个输入变量或常量.图给出了当𝑥 = 1, 𝑤 = 0, 𝑏 = 0 时复合函数𝑓(𝑥; 𝑤, 𝑏) 的计算图,其中连边上的红色数字表示前向计算时复合函数中每个变量的实际取值.
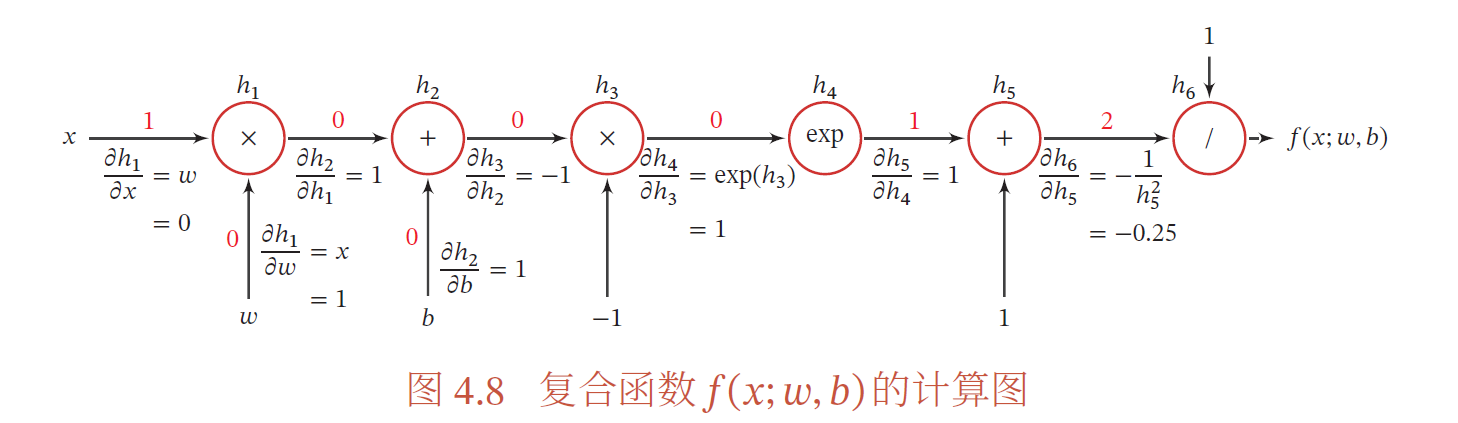
从计算图上可以看出,复合函数𝑓(𝑥; 𝑤, 𝑏) 由6 个基本函数ℎ𝑖, 1 ≤ 𝑖 ≤ 6 组成,每个基本函数的导数都十分简单,可以通过规则来实现.

梯度消失问题

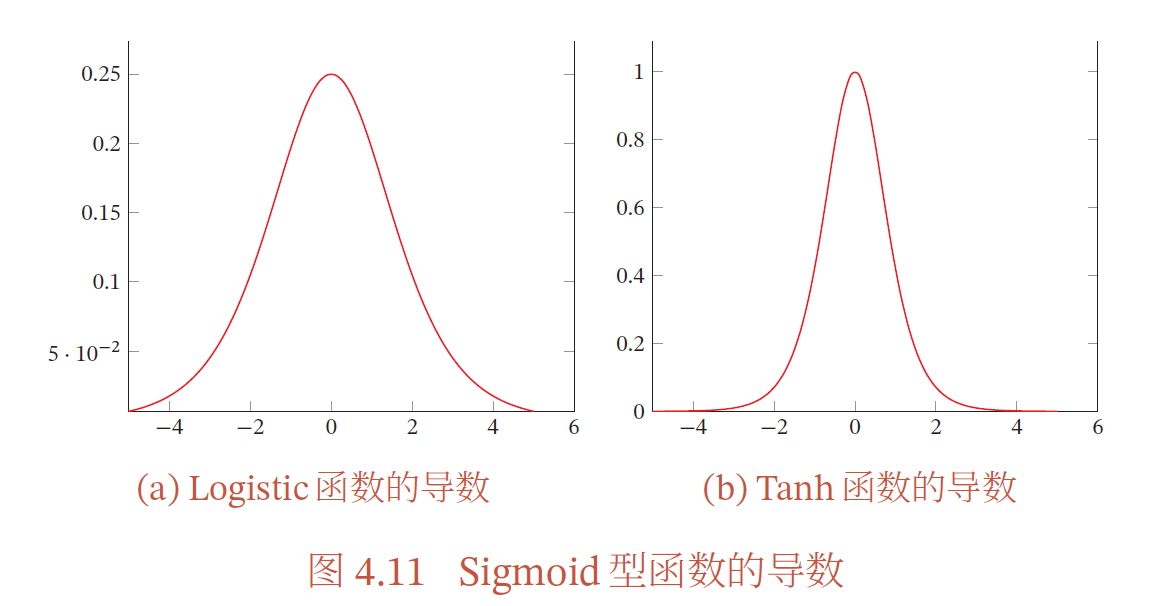
由于Sigmoid 型函数的饱和性,饱和区的导数更是接近于0.这样,误差经过每一层传递都会不断衰减.当网络层数很深时,梯度就会不停衰减,甚至消失,使得整个网络很难训练.这就是所谓的梯度消失问题
四、循环神经网络
循环神经网络(Recurrent Neural Network,RNN)是一类具有短期记忆能力的神经网络.在循环神经网络中,神经元不但可以接受其他神经元的信息,也可以接受自身的信息,形成具有环路的网络结构
循环神经网络在学习过程中的主要问题是由于梯度消失或爆炸问题,很难建模长时间间隔(Long Range)的状态之间的依赖关系.

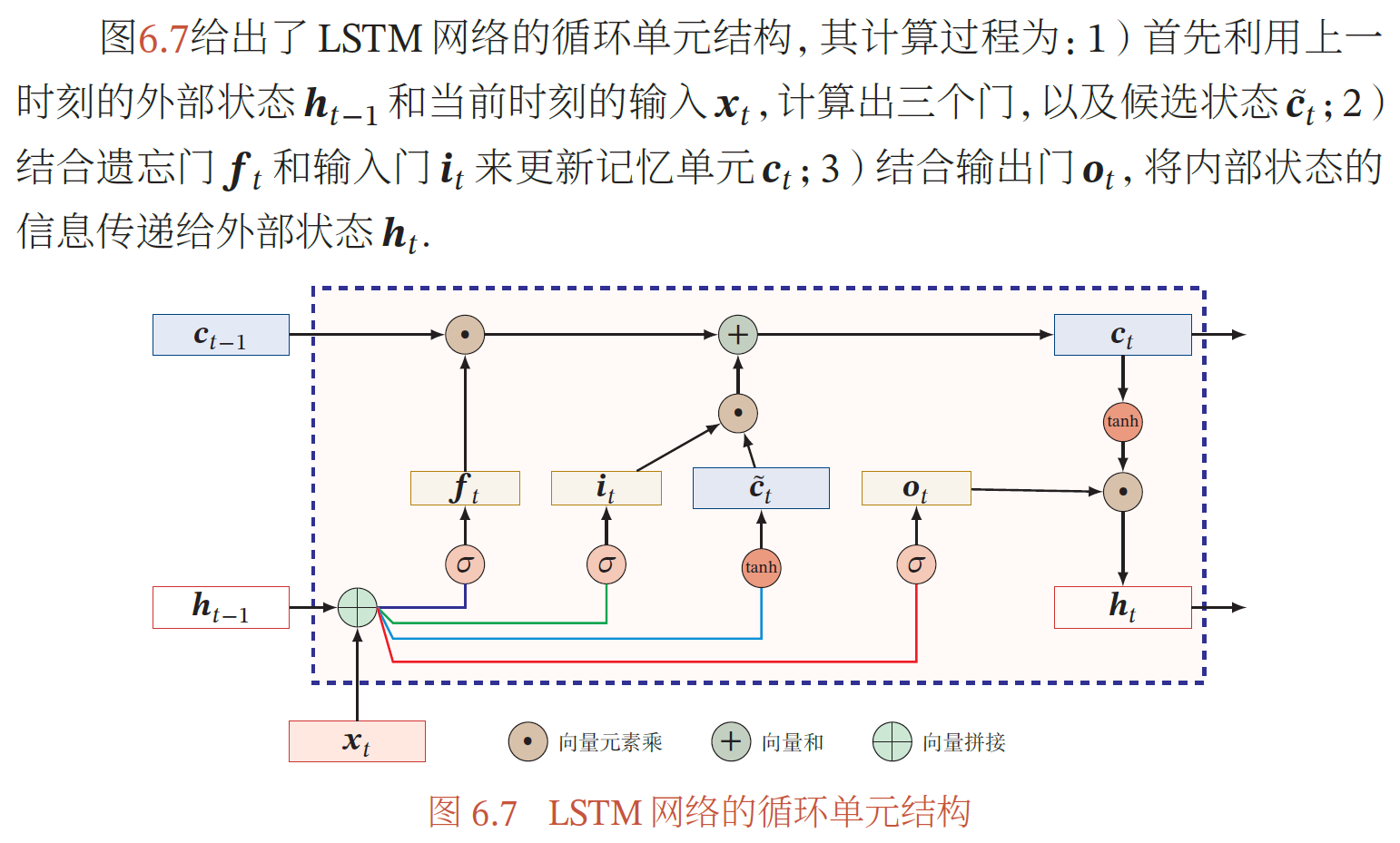
LSTM


当𝒇𝑡 = 0, 𝒊𝑡 = 1时,记忆单元将历史信息清空,并将候选状态向量𝒄𝑡̃ 写入.但此时记忆单元𝒄𝑡 依然和上一时刻的历史信息相关.当𝒇𝑡 = 1, 𝒊𝑡 = 0 时,记忆单元将复制上一时刻的内容,不写入新的信息.
LSTM 网络中的"门"是一种"软"门,取值在(0, 1) 之间,表示以一定的比例允许信息通过.三个门的计算方式为:
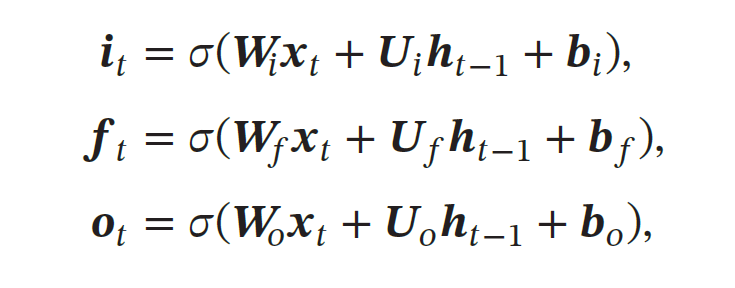
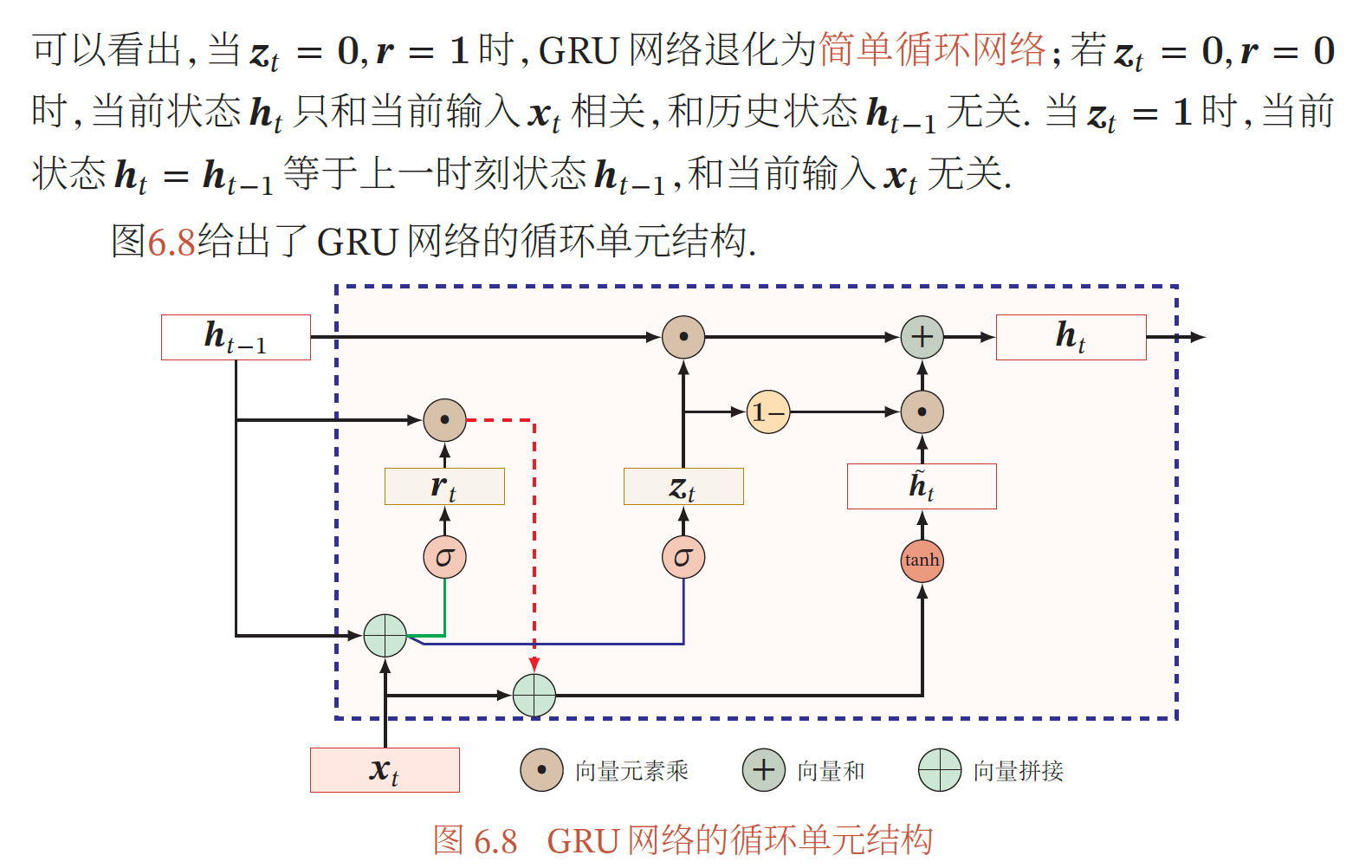
GRU

当𝒓𝑡 = 0时,候选状态𝒉𝑡̃ = tanh(𝑾𝑐𝒙𝑡 + 𝒃)只和当前输入𝒙𝑡相关,和历史状态无关.当𝒓𝑡 = 1时,候选状态𝒉𝑡̃ = tanh(𝑾ℎ𝒙𝑡 + 𝑼ℎ𝒉𝑡−1 + 𝒃ℎ)和当前输入𝒙𝑡 以及历史状态𝒉𝑡−1 相关,和简单循环网络一致.
五、网络优化与正则化
**优化问题:**深度神经网络的优化十分困难.首先,神经网络的损失函数是一个非凸函数,找到全局最优解通常比较困难.其次,深度神经网络的参数通常非常多,训练数据也比较大,因此也无法使用计算代价很高的二阶优化方法,而一阶优化方法的训练效率通常比较低.此外,深度神经网络存在梯度消失或爆炸问题,导致基于梯度的优化方法经常失效.
**泛化问题:**由于深度神经网络的复杂度比较高,并且拟合能力很强,很容易在训练集上产生过拟合.因此在训练深度神经网络时,同时也需要通过一定的正则化方法来改进网络的泛化能力.
目前,研究者从大量的实践中总结了一些经验方法,在神经网络的表示能力、复杂度、学习效率和泛化能力之间找到比较好的平衡,并得到一个好的网络模型.本章从网络优化和网络正则化两个方面来介绍这些方法.
网络优化
网络结构多样性:
由于网络结构的多样性,我们很难找到一种通用的优化方法.不同优化方法在不同网络结构上的表现也有比较大的差异.
高维变量的非凸优化:
低维空间的非凸优化问题主要是存在一些局部最优点.基于梯度下降的优化方法会陷入局部最优点,因此在低维空间中非凸优化的主要难点是如何选择初始化参数和逃离局部最优点
在高维空间中,非凸优化的难点并不在于如何逃离局部最优点,而是如何逃离**鞍点,**因鞍点的梯度是0,但是在一些维度上是最高点,在另一些维度上是最低点
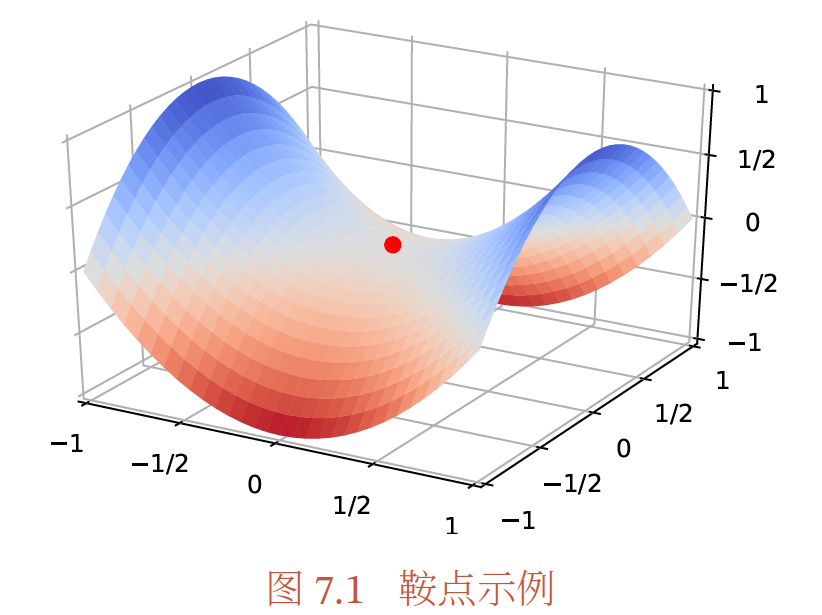
基于梯度下降的优化方法会在鞍点附近接近于停滞,很难从这些鞍点中逃离.因此,随机梯度下降对于高维空间中的非凸优化问题十分重要,通过在梯度方向上引入随机性,可以有效地逃离鞍点.
深度神经网络的参数非常多,并且有一定的冗余性,这使得每单个参数对最终损失的影响都比较小,因此会导致损失函数在局部最小解附近通常是一个平坦的区域,称为平坦最小值
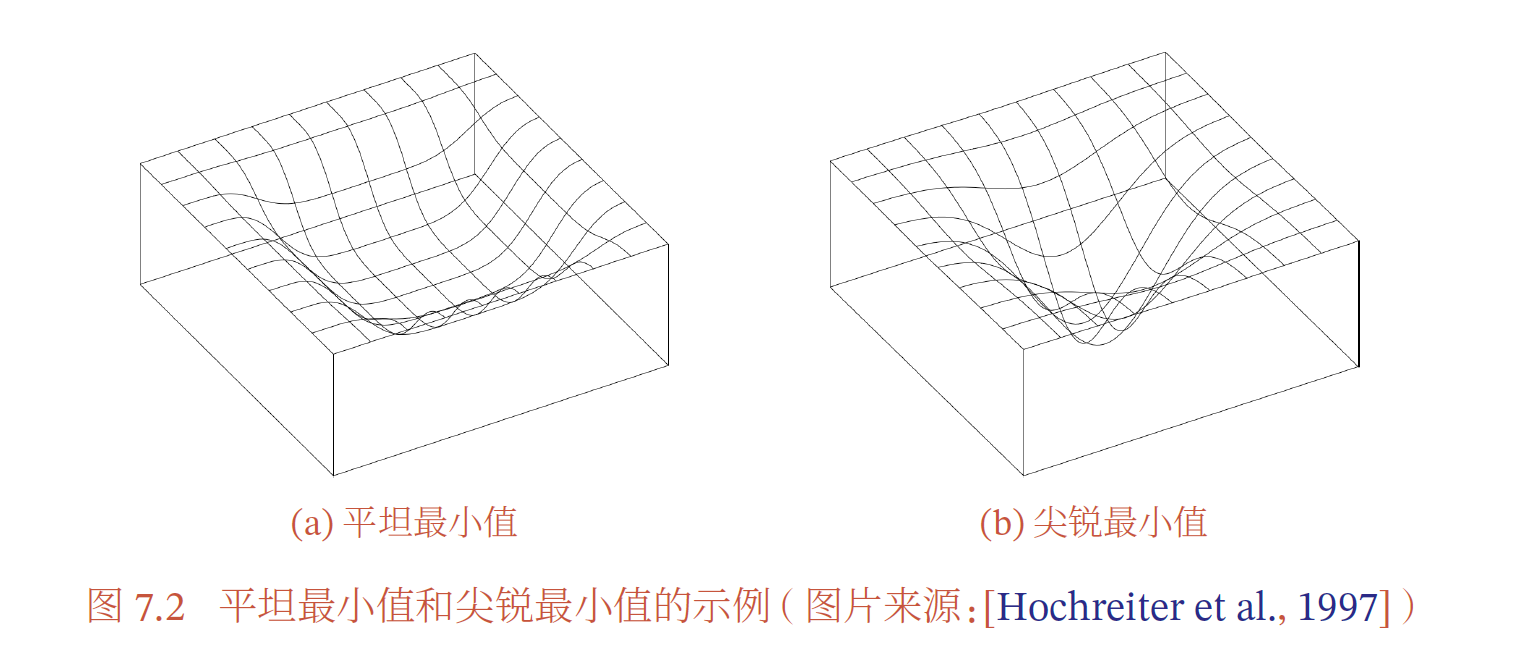
改善神经网络优化的目标是找到更好的局部最小值和提高优化效率.目前比较有效的经验性改善方法通常分为以下几个方面:
(1) 使用更有效的优化算法来提高梯度下降优化方法的效率和稳定性,比如动态学习率调整、梯度估计修正等.
(2) 使用更好的参数初始化方法、数据预处理方法来提高优化效率.
(3) 修改网络结构来得到更好的优化地形, 优化地形指在高维空间中损失函数的曲面形状.好的优化地形通常比较平滑.比如使用ReLU 激活函数、残差连接、逐层归一化等.
(4) 使用更好的超参数优化方法.
优化算法
在训练深度神经网络时,训练数据的规模通常都比较大.如果在梯度下降时,每次迭代都要计算整个训练数据上的梯度,这就需要比较多的计算资源.另外大规模训练集中的数据通常会非常冗余,也没有必要在整个训练集上计算梯度.因此,在训练深度神经网络时,经常使用小批量梯度下降法
批量大小选择:

学习率调整
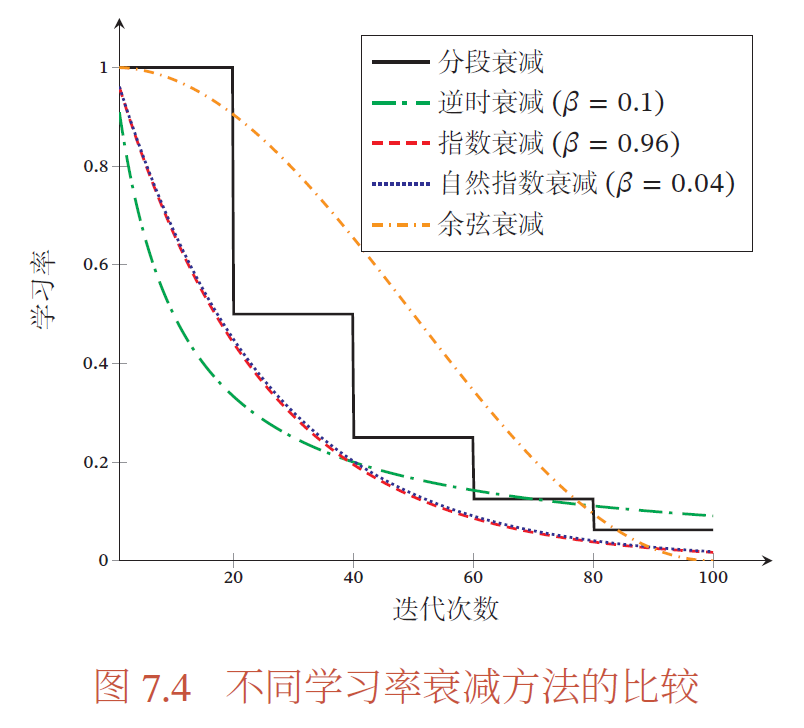
梯度估计修正
动量法:
动量法(MomentumMethod)是用之前积累动量来替代真正的梯度.每次迭代的梯度可以看作加速度.这样,每个参数的实际更新差值取决于最近一段时间内梯度的加权平均值.当某个参数在最近一段时间内的梯度方向不一致时,其真实的参数更新幅度变小;相反,当在最近一段时间内的梯度方向都一致时,其真实的参数更新幅度变大,起到加速作用
一般而言,在迭代初期,梯度方向都比较一致,动量法会起到加速作用,可以更快地到达最优点.在迭代后期,梯度方向会不一致,在收敛值附近振荡,动量法会起到减速作用,增加稳定性.从某种角度来说,当前梯度叠加上部分的上次梯度,一定程度上可以近似看作二阶梯度
Adam 算法:
可以看作动量法和RMSprop 算法的结合,不但使用动量作为参数更新方向,而且可以自适应调整学习率.Adam 算法一方面计算梯度平方g2𝑡 的指数加权平均(和RMSprop 算法类似),另一方面计算梯度g𝑡 的指数加权平均(和动量法类似).
梯度截断:
在基于梯度下降的优化过程中,如果梯度突然增大,用大的梯度更新参数反而会导致其远离最优点.为了避免这种情况,当梯度的模大于一定阈值时,就对梯度进行截断,称为梯度截断
数据预处理
归一化(Normalization)方法泛指把数据特征转换为相同尺度的方法,比如把数据特征映射到[0, 1] 或[−1, 1] 区间内,或者映射为服从均值为0、方差为1的标准正态分布
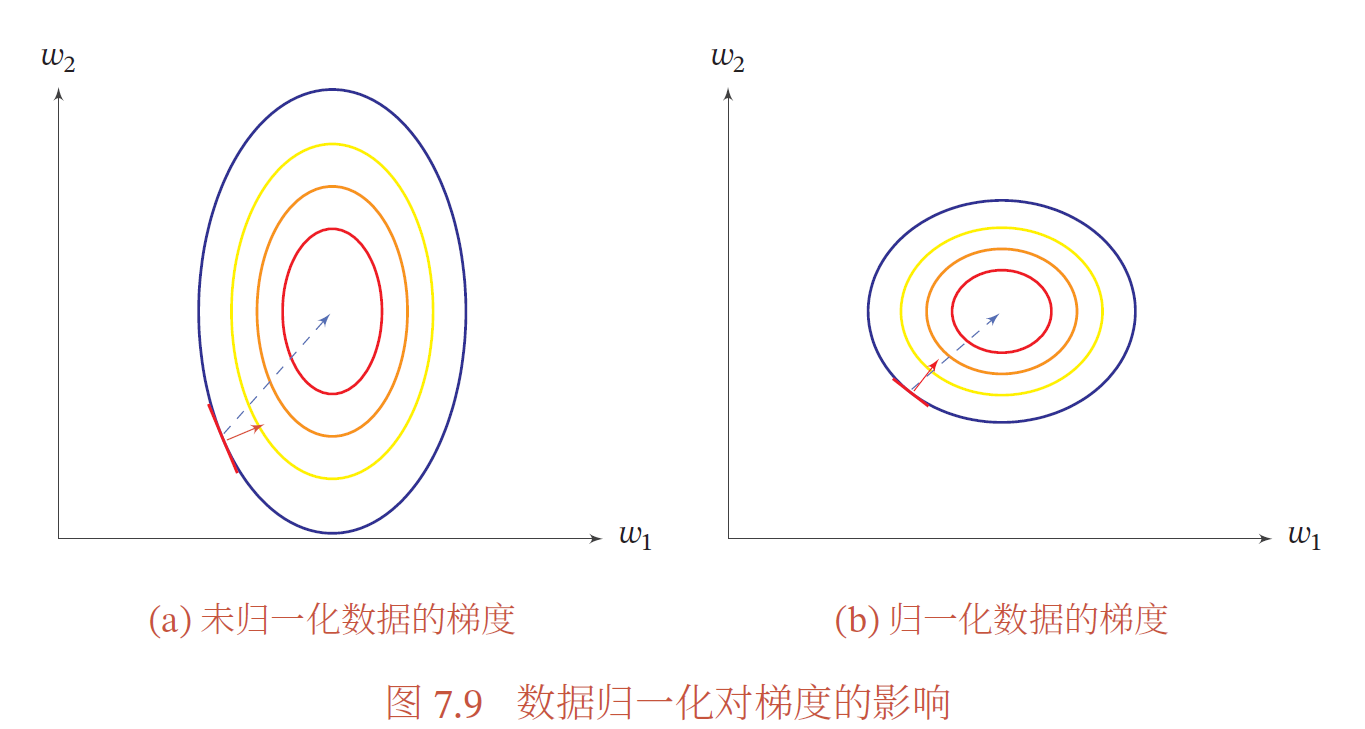


 逐层归一化
逐层归一化
是将传统机器学习中的数据归一化方法应用到深度神经网络中,对神经网络中隐藏层的输入进行归一化,从而使得网络更容易训练.包括:批量归一化、层归一化、权重归一化和局部响应归一化.
※ 批量归一化(Batch Normalization,BN)
对于一个深度神经网络,令第𝑙 层的净输入为𝒛(𝑙),神经元的输出为𝒂(𝑙),即
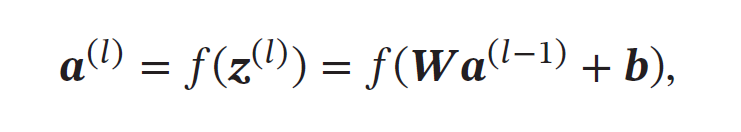
其中𝑓(⋅) 是激活函数,𝑾 和𝒃 是可学习的参数.
为了提高优化效率,就要使得净输入𝒛(𝑙) 的分布一致,比如都归一化到标准正态分布.虽然归一化操作也可以应用在输入𝒂(𝑙−1) 上,但归一化**𝒛(𝑙)**更加有利于优化.因此,在实践中归一化操作一般应用在仿射变换𝑾𝒂(𝑙−1) + 𝒃 之后、激活函数之前.
利用第7.4节中介绍的数据预处理方法对𝒛(𝑙) 进行归一化,相当于每一层都进行一次数据预处理,从而加速收敛速度.但是逐层归一化需要在中间层进行操作,要求效率比较高,因此复杂度比较高的白化方法就不太合适.为了提高归一化效率,一般使用标准化将净输入𝒛(𝑙) 的每一维都归一到标准正态分布.
批量归一化操作可以看作一个特殊的神经层,加在每一层非线性激活函数之前,即
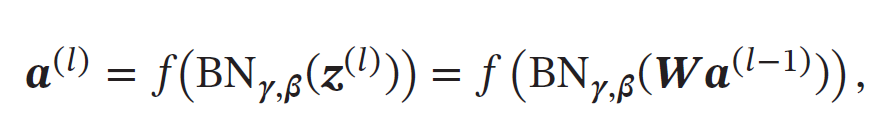
其中因为批量归一化本身具有平移变换,所以仿射变换𝑾𝒂(𝑙−1) 不再需要偏置参数。
值得一提的是,逐层归一化不但可以提高优化效率,还可以作为一种隐形的正则化方法.在训练时,神经网络对一个样本的预测不仅和该样本自身相关,也和同一批次中的其他样本相关.由于在选取批次时具有随机性,因此使得神经网络不会"过拟合"到某个特定样本,从而提高网络的泛化能力
※ 层归一化(Layer Normalization,LN)
批量归一化是对一个中间层的单个神经元进行归一化操作,因此要求小批量样本的数量不能太小,否则难以计算单个神经元的统计信息.此外,如果一个神经元的净输入的分布在神经网络中是动态变化 的,比如循环神经网络 ,那么就无法应用批量归一化操作.
层归一化(Layer Normalization)是和批量归一化非常类似的方法.和批量归一化不同的是,层归一化是对一个中间层的所有神经元进行归一化.
层归一化可以应用在循环神经网络中,对循环神经层进行归一化操作.假设在时刻𝑡,循环神经网络的隐藏层为𝒉𝑡,其层归一化的更新为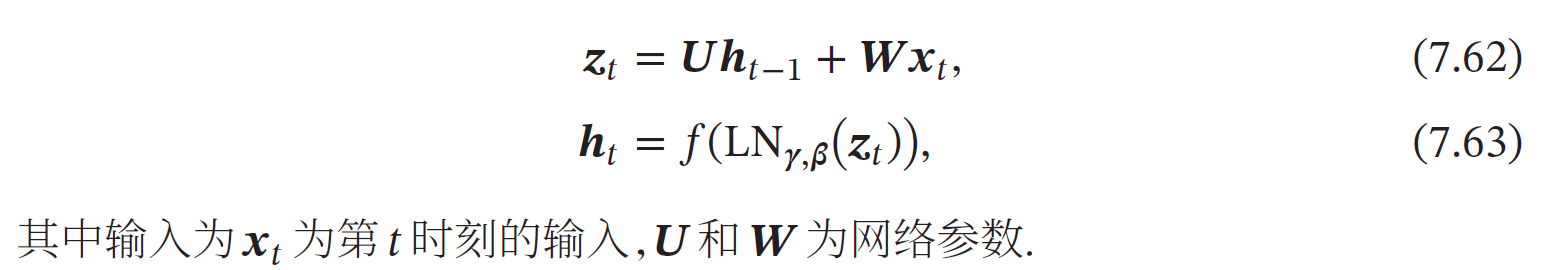
在标准循环神经网络中,循环神经层的净输入一般会随着时间慢慢变大或变小,从而导致梯度爆炸或消失.而层归一化的循环神经网络可以有效地缓解这种状况.
层归一化和批量归一化整体上是十分类似的,差别在于归一化的方法不同.对于𝐾 个样本的一个小批量集合𝒁(𝑙) = [𝒛(1,𝑙); ⋯ ; 𝒛(𝐾,𝑙)],层归一化是对矩阵𝒁(𝑙) 的每一列进行归一化,而批量归一化是对每一行进行归一化.一般而言,批量归一化是一种更好的选择.当小批量样本数量比较小时,可以选择层归一化.
超参数优化
常见的超参数有以下三类:
(1) 网络结构,包括神经元之间的连接关系、层数、每层的神经元数量、激活函数的类型等.
(2) 优化参数,包括优化方法、学习率、小批量的样本数量等.
(3) 正则化系数.
网络正则化
机器学习模型的关键是泛化问题,即在样本真实分布上的期望风险最小化.而训练数据集上的经验风险最小化和期望风险并不一致.由于神经网络的拟合能力非常强,其在训练数据上的错误率往往都可以降到非常低,甚至可以到0,从而导致过拟合.因此,如何提高神经网络的泛化能力反而成为影响模型能力的最关键因素.
正则化(Regularization)是一类通过限制模型复杂度,从而避免过拟合,提高泛化能力的方法,比如引入约束、增加先验、提前停止等.
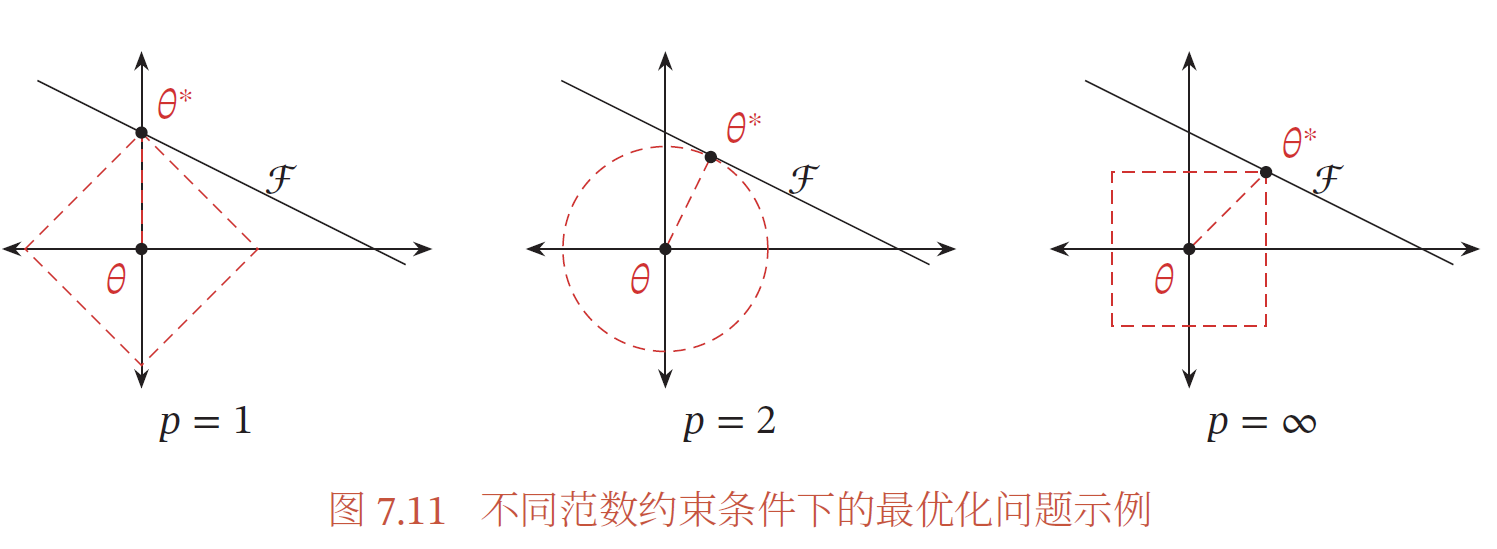
※ ℓ1 和ℓ2 正则化
ℓ1 和ℓ2 正则化是机器学习中最常用的正则化方法,通过约束参数的ℓ1 和ℓ2范数来减小模型在训练数据集上的过拟合现象,通过加入ℓ1 和ℓ2 正则化,优化问题可以写为
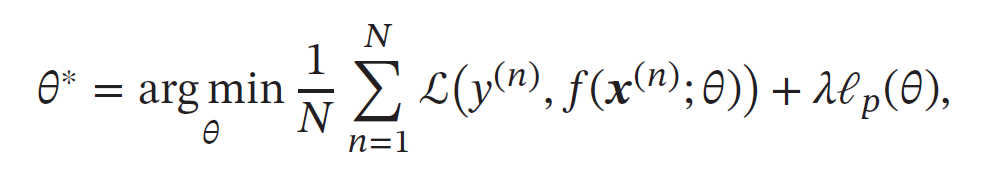
其中ℒ(⋅) 为损失函数,𝑁 为训练样本数量,𝑓(⋅) 为待学习的神经网络,𝜃 为其参数,
ℓ𝑝 为范数函数,𝑝 的取值通常为{1, 2} 代表ℓ1 和ℓ2 范数,𝜆 为正则化系数.
权重衰减

早停

dropout

六、注意力机制
用𝑿 = [𝒙1, ⋯ , 𝒙𝑁 ] ∈ ℝ𝐷×𝑁 表示𝑁 组输入信息,其中𝐷 维向量𝒙𝑛 ∈ℝ𝐷, 𝑛 ∈ [1, 𝑁] 表示一组输入信息.为了节省计算资源,不需要将所有信息都输入神经网络,只需要从𝑿 中选择一些和任务相关的信息.注意力机制的计算可以分为两步:一是在所有输入信息上计算注意力分布 ,二是根据注意力分布来计算输入信息的加权平均.
**注意力分布:**为了从𝑁 个输入向量[𝒙1, ⋯ , 𝒙𝑁 ] 中选择出和某个特定任务相关的信息,我们需要引入一个和任务相关的表示,称为查询向量(Query Vector),并通过一个打分函数来计算每个输入向量和查询向量之间的相关性.


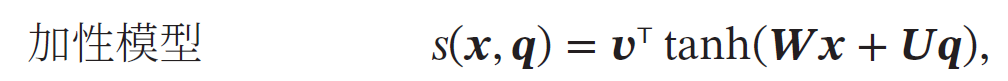
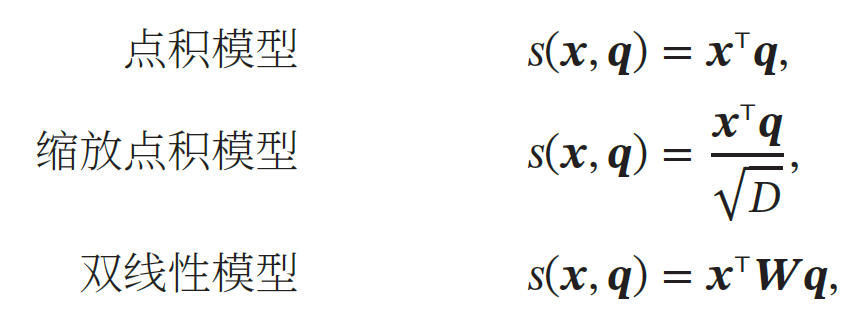
注意力分布𝛼𝑛 可以解释为在给定任务相关的查询𝒒 时,第𝑛 个输入向量受关注的程度.我们采用一种"软性"的信息选择机制对输入信息进行汇总,即
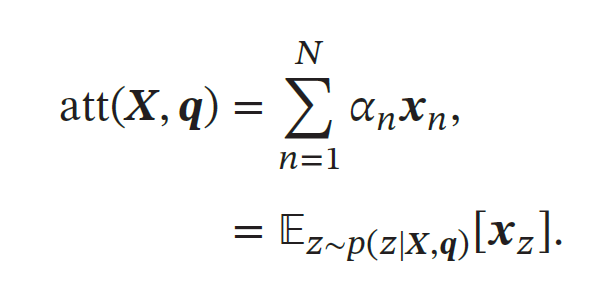
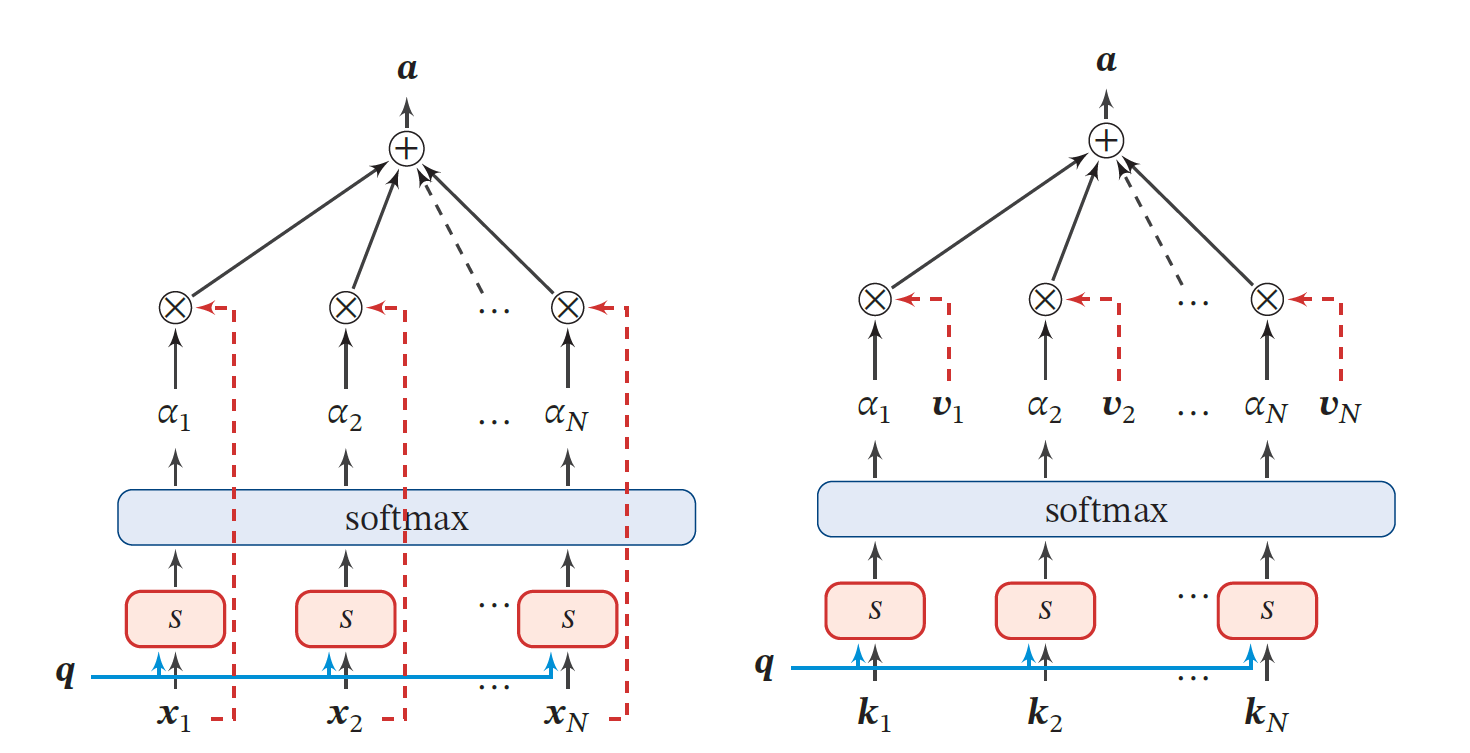
键值对注意力

多头注意力

自注意力
基于卷积或循环网络的序列编码都是一种局部的编码方式,只建模了输入信息的局部依赖关系.虽然循环网络理论上可以建立长距离依赖关系,但是由于信息传递的容量以及梯度消失问题,实际上也只能建立短距离依赖关系.
如果要建立输入序列之间的长距离依赖关系,可以使用以下两种方法:一种方法是增加网络的层数,通过一个深层网络来获取远距离的信息交互;另一种方法是使用全连接网络.全连接网络是一种非常直接的建模远距离依赖的模型,但是无法处理变长的输入序列.不同的输入长度,其连接权重的大小也是不同的.这时我们就可以利用注意力机制来"动态"地生成不同连接的权重,这就是自注意力模型(Self-Attention Model)
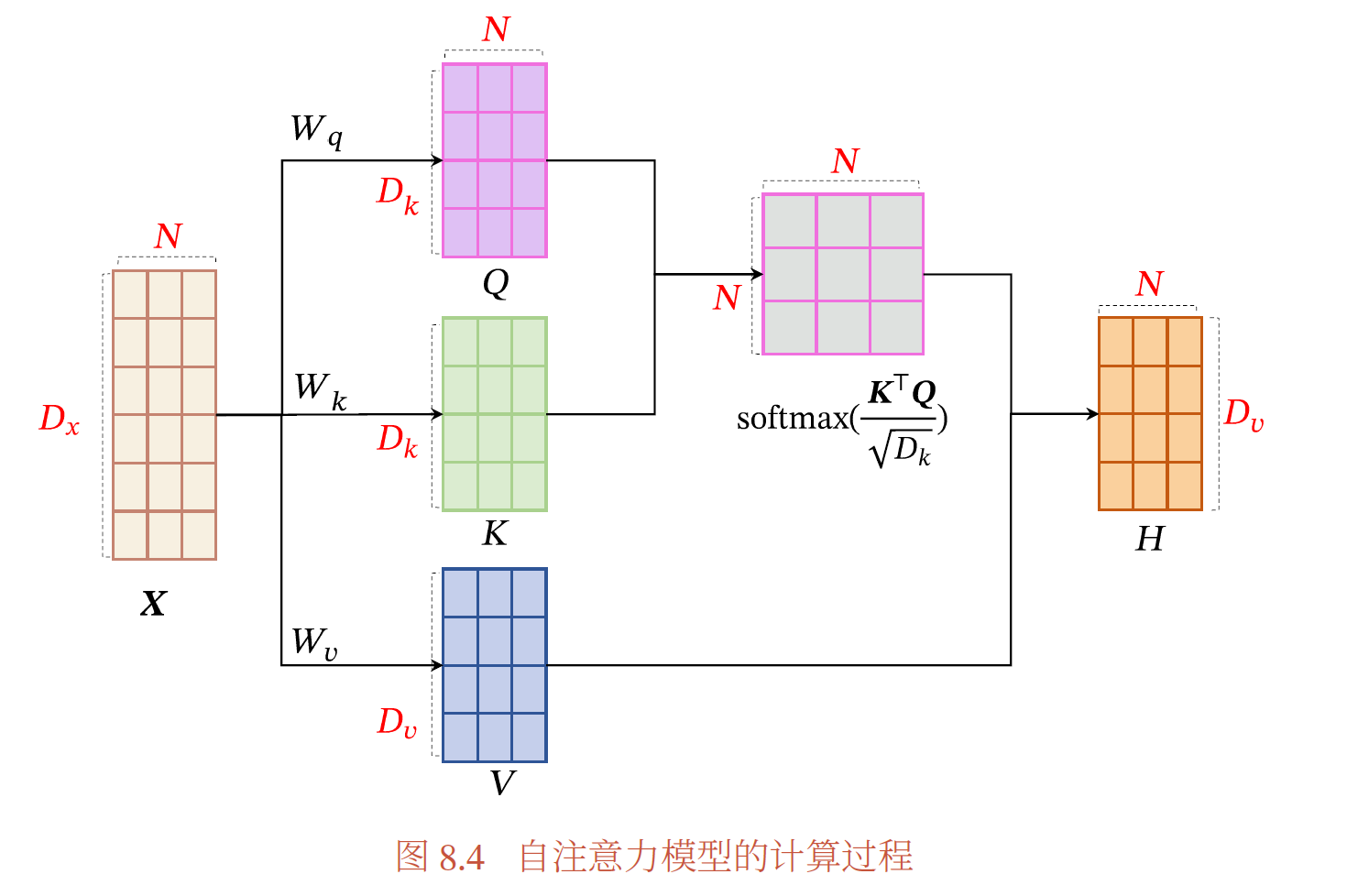
为了提高模型能力,自注意力模型经常采用查询-键-值**(Query-Key-Value,QKV)**模式,其计算过程如图8.4所示,其中红色字母表示矩阵的维度.



七、序列生成模型
为了有效地描述自然语言规则,我们可以从统计的角度来建模.将一个长度为𝑇 的文本序列看作一个随机事件𝑋1∶𝑇 = ⟨𝑋1, ⋯ , 𝑋𝑇 ⟩,其中每个位置上的变量𝑋𝑡 的样本空间为一个给定的词表(vocabulary)𝒱,整个序列𝒙1∶𝑇 的样本空间为|𝒱|𝑇.
深度序列模型
深度序列模型(Deep Sequence Model)是指利用神经网络模型来估计条件概率𝑝𝜃(𝑥𝑡|𝒙1∶(𝑡−1)).假设一个神经网络𝑓(⋅; 𝜃),其输入为历史信息ℎ𝑡̃ = 𝒙1∶(𝑡−1),输出为词表𝒱 中的每个词𝑣𝑘(1 ≤ 𝑘 ≤ |𝒱|) 出现的概率,并满足
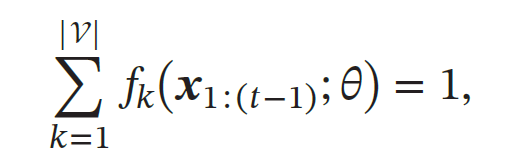
深度序列模型一般可以分为三个模块:嵌入层、特征层、输出层.
嵌入层
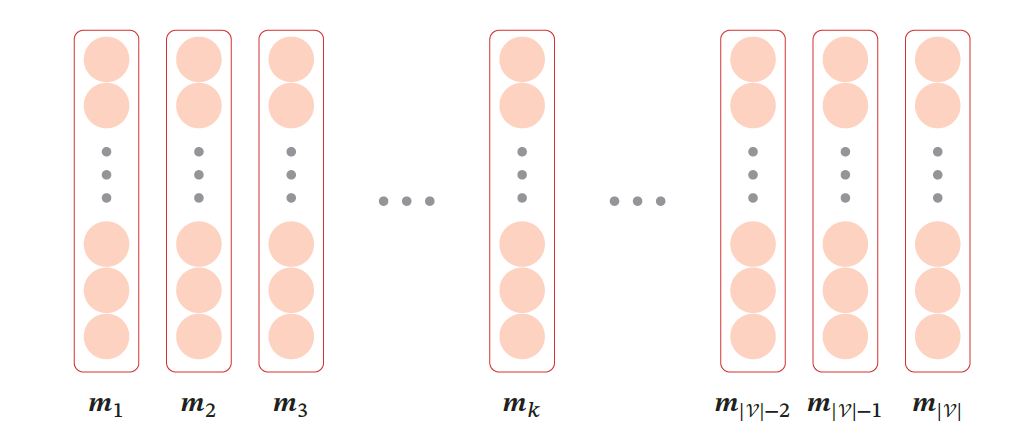
令ℎ𝑡̃ = 𝒙1∶(𝑡−1) 表示输入的历史信息,一般为符号序列.由于神经网络模型一般要求输入形式为实数向量,因此为了使得神经网络模型能处理符号数据,需要将这些符号转换为向量形式.一种简单的转换方法是通过一个嵌入表(Embedding Lookup Table)来将每个符号直接映射成向量表示.嵌入表也称为嵌入矩阵或查询表.图15.2是嵌入矩阵的示例

特征层
特征层用于从输入向量序列𝒆1, ⋯ , 𝒆𝑡−1 中提取特征,输出为一个可以表示历史信息的向量𝒉𝑡.
特征层可以通过不同类型的神经网络(比如前馈神经网络和循环神经网络等)来实现.
输出层
输出层一般使用Softmax 分类器,接受历史信息的向量表示𝒉𝑡 ∈ ℝ𝐷ℎ,输出为词表中每个词的后验概率,输出大小为|𝒱|.
评价指标
给定一个测试文本集合,一个好的序列生成模型应该使得测试集合中句子的联合概率尽可能高.
困惑度
可以衡量模型分布与样本经验分布之间的契合程度.困惑度越低则两个分布越接近
BLEU
算法是一种衡量模型生成序列和参考序列之间的N 元词组(N-Gram)重合度的算法,最早用来评价机器翻译模型的质量,目前也广泛应用在各种序列生成任务中。
算法的值域范围是[0, 1],越大表明生成的质量越好.但是BLEU 算法只计算精度,而不关心召回率(即参考序列里的N 元组合是否在生成序列中出现)
ROUGE
和BLEU 算法类似,但ROUGE 算法计算的是召回率
Seq2Seq
是一种条件的序列生成问题,给定一个序列𝒙1∶𝑆,生成另一个序列𝒚1∶𝑇.输入序列的长度𝑆 和输出序列的长度𝑇 可以不同
.比如在机器翻译中,输入为源语言,输出为目标语言.图15.5给出了基于循环神经网络的序列到序列机器翻译示例,其中⟨𝐸𝑂𝑆⟩ 表示输入序列的结束,虚线表示用上一步的输出作为下一步的输入.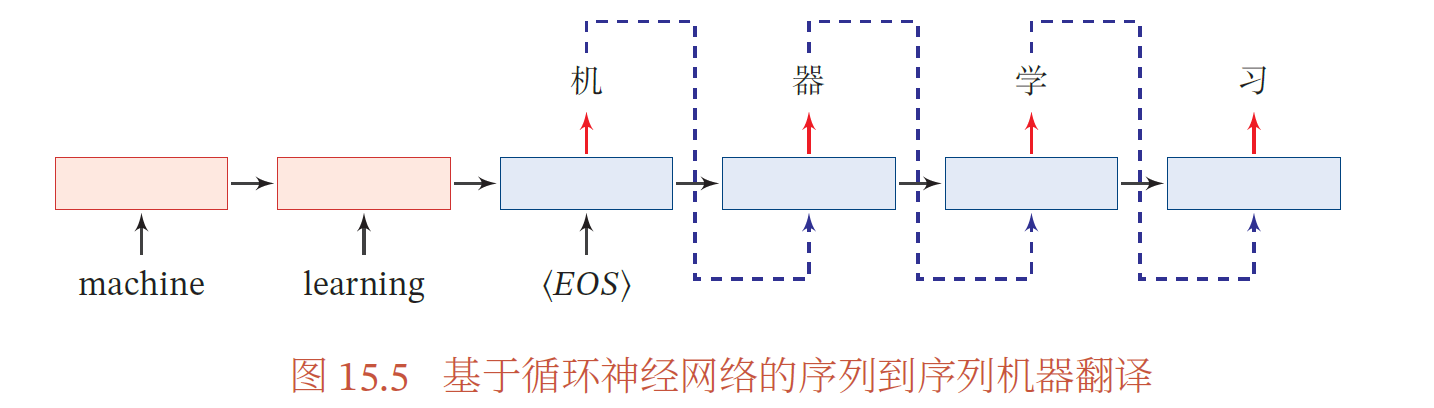
基于循环神经网络的Seq2Seq模型
实现序列到序列的最直接方法是使用两个循环神经网络来分别进行编码和解码,也称为编码器-解码器(Encoder-Decoder)模型.
编码器:首先使用一个循环神经网络𝑓enc 来编码输入序列𝒙1∶𝑆 得到一个固定维数的向量𝒖,𝒖 一般为编码循环神经网络最后时刻的隐状态.被用作整个输入序列的语义摘要
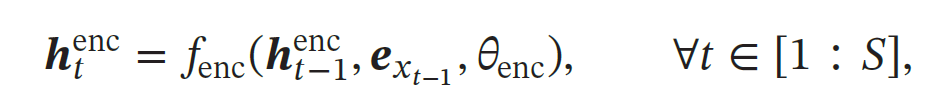
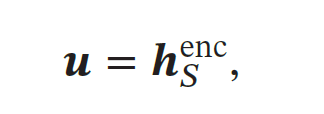
其中𝑓enc(⋅) 为编码循环神经网络,可以为LSTM 或GRU,其参数为𝜃enc,𝒆𝑥 为词𝑥的词向量.解码器的初始隐藏状态 直接设置为编码器产出的上下文向量 u。从上下文向量 u开始,逐步生成输出序列。
解码器:在生成目标序列时,使用另外一个循环神经网络𝑓dec 来进行解码.在解码过程的第𝑡 步时,已生成前缀序列为𝒚1∶(𝑡−1)
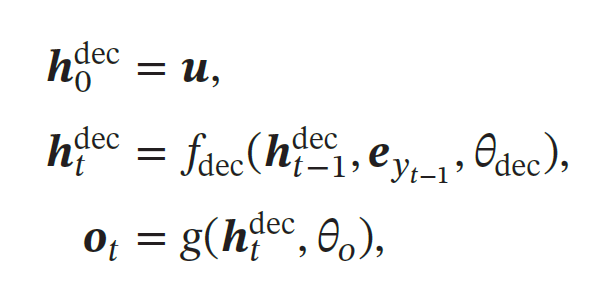
其中𝑓dec(⋅) 为解码循环神经网络,𝑔(⋅) 为最后一层为Softmax 函数的前馈神经网络,𝜃dec 和𝜃𝑜 为网络参数,𝒆𝑦 为𝑦 的词向量,𝑦0 为一个特殊符号,比如⟨𝐸𝑂𝑆⟩.
基于循环神经网络的序列到序列模型的缺点是:1)编码向量𝒖 的容量问题,输入序列的信息很难全部保存在一个固定维度的向量中;2)当序列很长时,由于循环神经网络的长程依赖问题,容易丢失输入序列的信息.
基于注意力的Seq2Seq模型


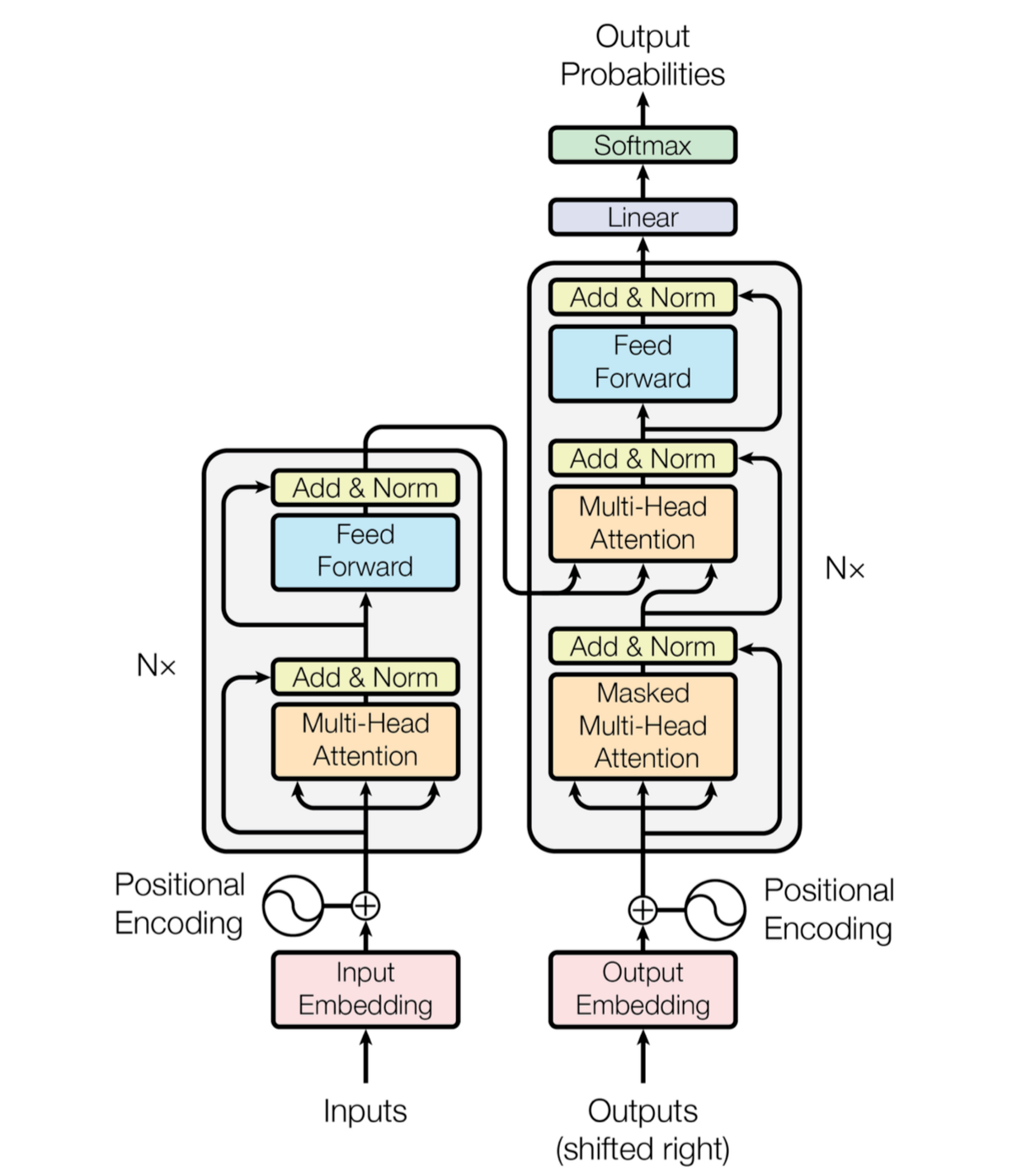
Transormer基于自注意力的序列到序列模型