**一、计算层（**Compute ）分类
在AI算子（Operator）分类中，按计算密集度和访存特性分为三类：
第一类计算（Compute-Bound/Compute-Intensive）：计算密集型算子
特点：
- 计算量远大于访问量
- 计算/访存比（Arithmetic Intensity）高
- 性能瓶颈在计算单元（如GPU的CUDA Core、NPU的MAC单元）
- 对带宽要求相对较低
典型算子：矩阵乘法（GEMM）、卷积（Conv2D）、全连接层（FC）、BatchNorm
第二类计算（Memory-Bound ）：访存密集型算子
特点：
- 访存量大，计算量小
- 性能瓶颈在内存带宽
- 计算单元利用率低
典型算子：ReLU、Sigmoid、Tanh、Pooling、Element-wise操作（加法、乘法、Scale）、Reshape、Transpose
第三类计算（Communication-Bound ）：通信密集型算子
特点：
- 涉及跨设备/跨节点数据传输
- 性能瓶颈在网络带宽或设备间互联
典型算子：AllReduce、AllGather、Send/Recv（多卡通信）
**二、存储层（**Memory ）分类
第一类内存（Primary Memory / On-Chip Memory ）：片上存储器
特点：
- 位于处理器芯片内部
- 速度极快（ns级延迟）
- 容量小（KB-MB级）
- 成本高
典型类型：
|-------------------|-----------|---------|--------|----------|
| 名称 | 容量 | 延迟 | 带宽 | 用途 |
| 寄存器（Register） | 几十KB | <1ns | 极高 | 临时存储操作数 |
| L1 Cache | 32-128KB | 1-4ns | TB/s级 | 指令/数据缓存 |
| L2 Cache | 256KB-1MB | 5-12ns | 数百GB/s | 共享缓存 |
| L3 Cache | 8-64MB | 20-50ns | 数百GB/s | 多核共享缓存 |
| SRAM（片上缓冲） | 几MB | <10ns | TB/s级 | NPU的片上缓存 |
第二类内存（Secondary Memory / Off-Chip Memory ）：片外主存储器
特点：
- 位于芯片外部
- 速度较快（数十-百ns级）
- 容量中等（GB-数十GB）
- 主要用于模型和中间数据存储
典型类型：
|-------------------|---------|-------------|----------|------------|
| 名称 | 容量 | 带宽 | 延迟 | 用途 |
| DDR SDRAM | 8-128GB | 50-100GB/s | 50-100ns | CPU主存 |
| GDDR（显存） | 8-24GB | 500-900GB/s | 数十ns | GPU显存 |
| HBM/HBM2/HBM3 | 16-80GB | 1-3TB/s | 数十ns | 高端GPU/AI芯片 |
第三类内存（Tertiary Memory / Storage ）：外部存储设备
特点：
- 速度慢（ms-秒级）
- 容量极大（TB-PB级）
- 成本低
- 用于持久化存储
典型类型：
|---------------|-----------|-------------|---------|---------|
| 名称 | 容量 | 带宽 | 延迟 | 用途 |
| SSD | 256GB-8TB | 3-7GB/s | 0.1-1ms | 数据集存储 |
| HDD | 1-20TB | 100-200MB/s | 5-10ms | 大规模数据存储 |
| 网络存储（NAS） | PB级 | 1-10GB/s | 数ms-秒 | 分布式数据集 |
三、常见****AI 算子介绍
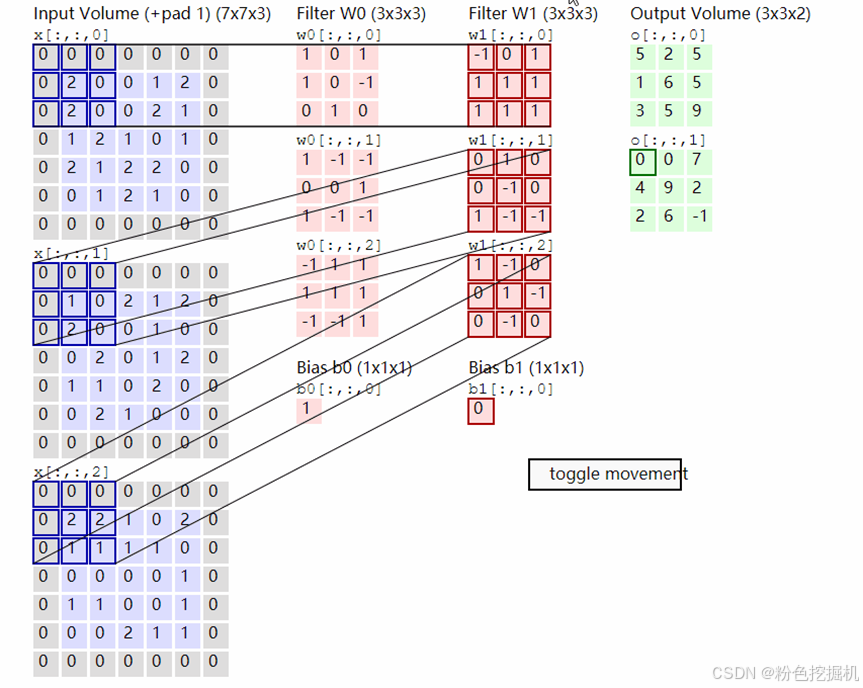
Conv2d
单通道Conv2d算子数学表达式为：
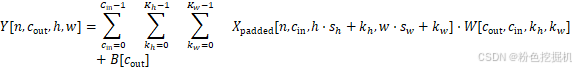
输出张量：Y[n, c out*,h,w]*
|-------|------------|----------------|--------------------|
| n | 批次索引 | 0≤n<N | 当前样本在批次中的位置（第n个图像） |
| cout | 输出通道索引 | 0≤cout<Cout | 当前卷积核的索引 |
| h | 输出高度索引 | 0≤h<Hout | 输出特征图的行位置 |
| w | 输出宽度索引 | 0≤w<Wout | 输出特征图的列位置 |
注：对于上述Conv2d数字表达式来说，h⋅ s h + k h ,w⋅ s w + kw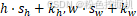 
坐标计数包括padding，表示输入提取的左上像素坐标；如果不包括padding，则表示中心点坐标，那么公式中的求和范围需要根据padding行数进行对应修改。
输入张量：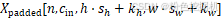
|-----------|------------|--------------|----------------------|
| 参数 | 含义 | 范围 | 说明 |
| n | 批次索引 | 0≤n<N | 与输出的批次对应 |
| cin | 输入通道索引 | 0≤cin<Cin | 输入特征图的通道（如RGB的R/G/B） |
| h⋅sh+kh | 输入高度位置 | - | 卷积窗口在输入上的垂直位置 |
| w⋅sw+kw | 输入宽度位置 | - | 卷积窗口在输入上的水平位置 |
其中，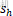
、
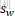为：
|--------|----------|---------|---------------|
| 参数 | 含义 | 典型值 | 说明 |
| sh | 垂直步长 | 1, 2 | 卷积核垂直方向移动的像素数 |
| sw | 水平步长 | 1, 2 | 卷积核水平方向移动的像素数 |
权重张量：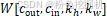
|--------|-------------|----------------|------------|
| 参数 | 含义 | 范围 | 说明 |
| cout | 输出通道索引 | 0≤cout<Cout | 第几个卷积核 |
| cin | 输入通道索引 | 0≤cin<Cin | 卷积核对应的输入通道 |
| kh | 卷积核高度偏移 | 0≤kh<Kh | 卷积核内的行位置 |
| kw | 卷积核宽度偏移 | 0≤kw<Kw | 卷积核内的列位置 |
偏置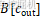
|--------|------------|----------------|--------------|
| 参数 | 含义 | 范围 | 说明 |
| cout | 输出通道索引 | 0≤cout<Cout | 每个卷积核对应一个偏置值 |
原理示意图：
GEMM**（** General Matrix Multiply ）
矩阵乘法算子，是线性代数和深度学习中最重要的基础运算之一。
GEMM标准形式为：
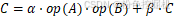
其中
- A 是 m ×k 矩阵
- B 是k ×n 矩阵
- C 是 m ×n 矩阵
- α 和 β 是标量系数
- op (X ) 表示对矩阵 X 的可选操作（转置或不转置）
GEMM应用场景：
深度学习：全连接层、卷积运算的实现基础
科学计算：线性系统求解、特征值分解
图形处理：变换矩阵运算
信号处理：滤波器设计、频域分析
im2col**（** Image to Column ）
im2col是深度学习中用于加速卷积计算的核心预处理技术，它的本质是将二维矩阵转换为一维向量矩阵进行存储，使卷积的局部滑动窗口操作转化为矩阵乘法友好的形式，为后续的GEMM（通用矩阵乘法）优化铺路。几乎所有主流深度学习框架（PyTorch、TensorFlow、Caffe）的卷积层都采用im2col+GEMM的优化策略，是工业界卷积加速的标准方案。
如图所示：
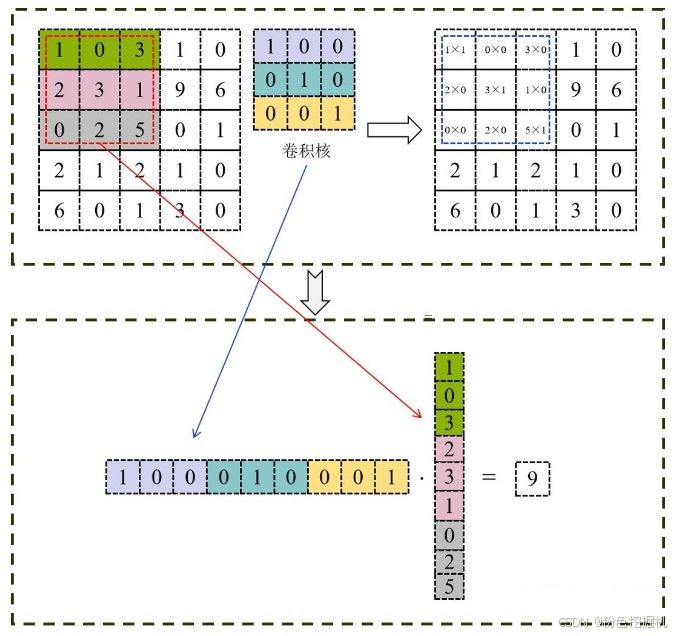
im2col+GEMM**（卷积加速的工业级标准方案）**
解决普通卷积计算的两大瓶颈：
零散内存访问：普通卷积逐窗口滑动时，输入元素分布在内存非连续区域，缓存命中率低；
并行性不足：GPU擅长密集型并行计算（如矩阵乘法），但局部窗口操作难以利用其 thousands of threads 的优势。
im2col+GEMM通过"输入展开→矩阵乘法→结果重塑"的流程，将卷积转化为高效的矩阵运算。
详细计算流程：
使用 Im2Col 将输入矩阵展开为一个大矩阵，矩阵每一列表示卷积核需要的一个输入数据，按向量方式存储；将卷积核展开为行矩阵进行存储。
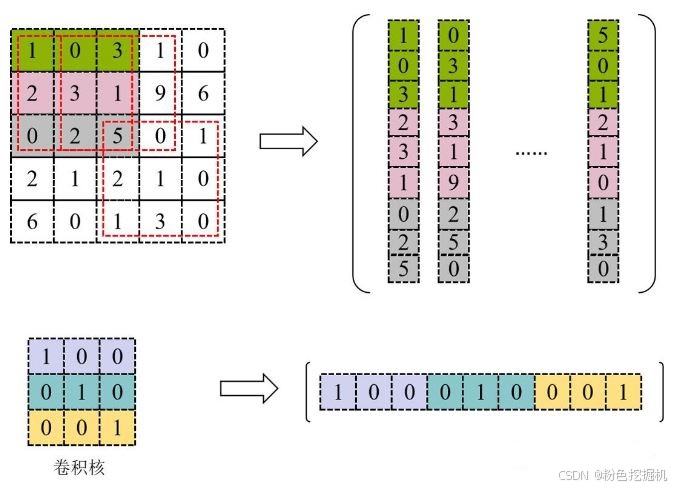
使用上图中转换的矩阵进行GEMM运算，得到的数据再进行col2im就是最终卷积计算的就结果。
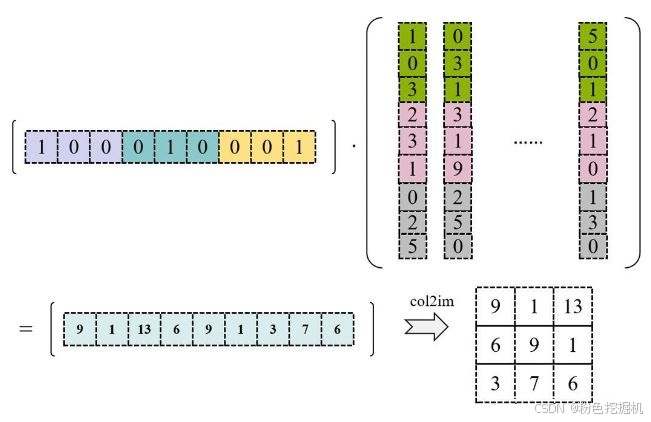
直接卷积与该卷积加速方法对比：
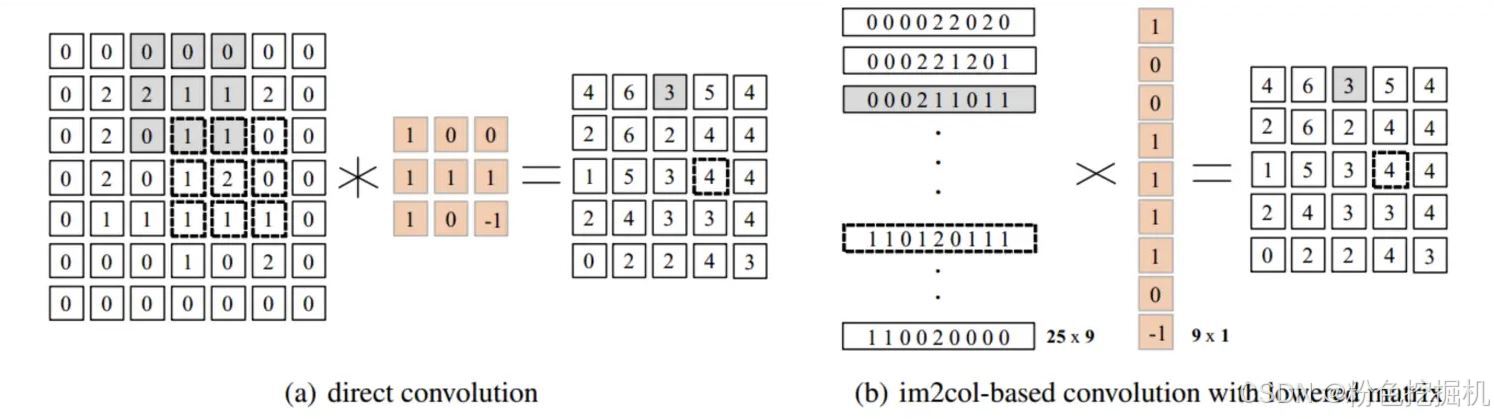
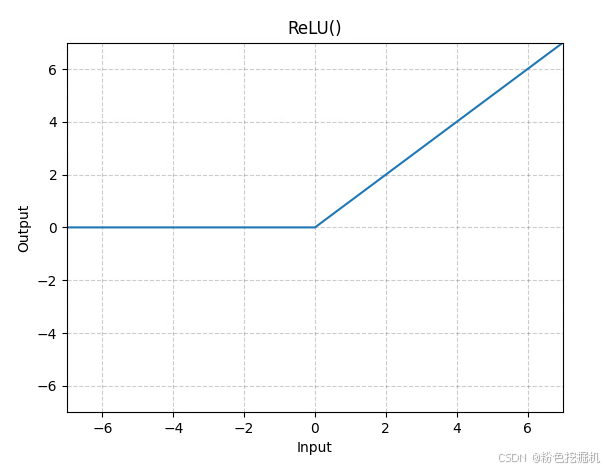
ReLU**（** Rectified Linear Unit，修正线性单元）
数学表达式：
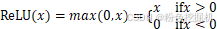
图形表示：
