摘要：
文章提出N-BEATS这一基于深度全连接层和双向残差链接的神经网络架构，用于单变量时间序列点预测，包含通用（N-BEATS-G）和可解释（N-BEATS-I）两种配置，无需时间序列特定组件即可在M3、M4、TOURISM等数据集上实现最先进性能，较 M4 竞赛冠军准确率提升 3%，且通过趋势（多项式基）和季节性（傅里叶基）分解实现可解释性，同时借助集成学习进一步优化效果。
介绍：
时间序列预测是一个很重要的问题，精准度提升可带来显著经济价值。深度学习在计算机视觉、NLP 领域已成熟，但在时间序列预测中，传统统计方法（如指数平滑、ARIMA）和混合模型仍占优。文章提出的·研究目标就是验证纯深度学习架构的潜力，同时设计兼具准确性与可解释性的模型。
任务单变量的离散时间点预测，给定长度T的历史序列y1,y2,y3....yn，预测未来的H个值[yn
+1,yn+2.....yn+H]。输入为长度为2H~7H的回溯窗口x=yn-t+1...yn。
N-BEATS：
首先，基础架构应该是简单和通用的，但又具有表现力(深度)。其次，架构不应该依赖于特定于时间序列的功能工程或输入缩放。
BASIC BLOCK
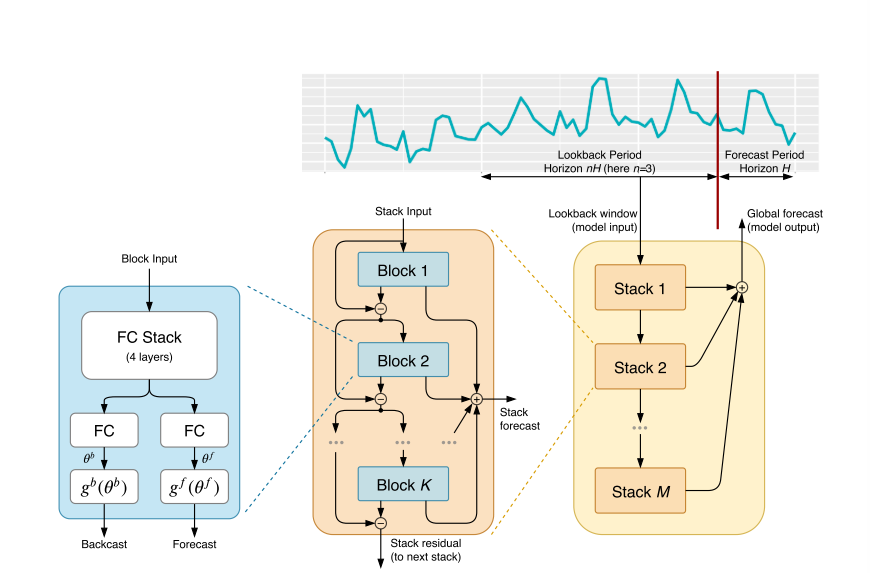
基础模块是一个 "分叉结构" 的全连接网络，核心作用是同时输出 "部分预测结果 " 和 "输入信号拟合结果"。
输入是前一个模块的残差信号，输出分为两个，一个是模块的部分预测，长度等于预测长度，另一个是模块的回溯拟合，长度和输入一致，是模块对输入信号的最佳拟合（相当于提取输入中的可解释成分，比如趋势、季节性）。
核心组件是也是两部分，第一个由四层全连接层的FC Stack，输出两个 "基扩展系数"：正向系数θf（用于生成预测y）和反向系数θb（用于生成回溯拟合x）；另一部分是也是两个全连接层，分别接收正向系数θf和反向系数θb，生成部分预测和回溯拟合。
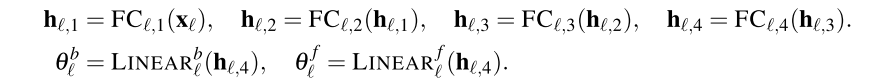
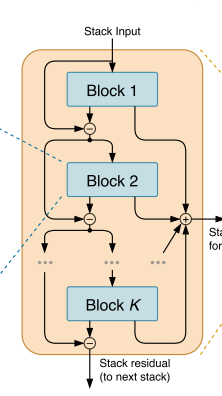
DOUBLY RESIDUAL STACKING
双向残差堆叠（Doubly Residual Stacking），这是 N-BEATS 的拓扑核心，解决了传统残差网络难以解释、训练深层模型困难的问题，同时实现了预测的分层聚合。
传统残差网络（ResNet）和密集连接网络（DenseNet）仅关注 "输入 - 输出" 的单一残差链接，网络内部结构难以解释。无法实现预测结果的分层分解，不利于提取趋势、季节性等可解释成分。N-BEATS 的创新：设计两条并行残差分支，同时解决 "深层训练" 和 "可解释性" 两大问题。
回溯残差分支（处理输入信号） ：逐步移除输入中已被拟合的成分，让后续模块专注于未捕捉的信号。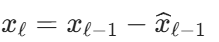
前一个模块先 "吃透" 输入中能解释的部分（比如季节性波动），把剩下的 "难啃" 残差传给下一个模块，逐步细化特征提取。
预测聚合分支（生成最终预测) ：每个模块输出 "部分预测"，最终累加得到总预测，实现分层预测。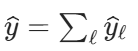
每个模块都贡献一小部分预测（比如 A 模块预测趋势、B 模块预测季节性），最后加起来得到完整预测。
INTERPRETABILITY
N-BEATS 通过两种配置实现 "通用泛化" 与 "可解释性" 的平衡，可解释配置通过注入趋势 / 季节性归纳偏置，将预测分解为人类可理解的成分，且无明显性能损失。
两种不同的配置的主要区别就是基函数的设计的不同，通用型使用线性层，可解释型使用低次多项式/傅里叶级数。
通用配置的 "分解" 是数据驱动的无约束分解：网络自主学到的基波形没有固定规律，只是为了拟合数据而存在的 "抽象模式"，人类无法将其与趋势、季节性等可理解的因素对应，因此缺乏可解释性 ------ 这也是它和 "可解释配置（N-BEATS-I）" 的核心区别（后者会强制基函数是多项式 / 傅里叶级数，有明确物理含义）。
