线性回归VS逻辑回归：解析与实战

线性回归（Linear Regression）和逻辑回归（Logistic Regression）是机器学习中最基础、最重要的两种监督学习算法。

---

一、线性回归

1、原理介绍

核心目标

预测连续值（如房价、温度、销售额）。

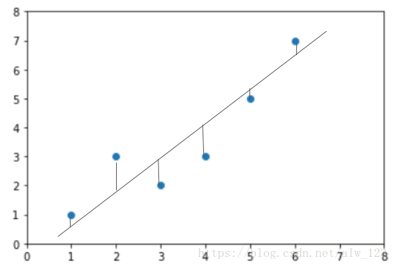
基本思想

假设特征（输入）与目标（输出）之间存在线性关系 ，通过拟合一条"最佳直线"（或超平面）来预测新数据。寻找最佳直线的过程就是在做线性回归。

数学模型

对于一个样本 x=(x1,x2,...,xn)x=(x1​,x2​,...,xn​) ，预测值为：

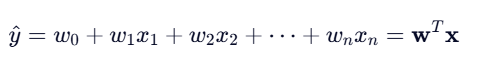
• w=(w0,w1,...,wn)w=(w0,w1,...,wn) ：模型参数（ w0是偏置项）
• y^ ：预测的连续值（如 50.3 万元）

损失函数

如何衡量**"最佳"** ？使用 均方误差（MSE）：

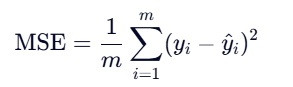
欧氏距离其实就是用来量化预测结果和真实结果的误差的一个函数。在线性回归中称呼他为损失函数，也就是计算误差的函数。

目标：最小化 MSE → 找到最优 w（模型参数）

求解方法

• 正规方程：直接解析解（适合小数据）
• 梯度下降）：迭代优化（适合大数据）

2、实战代码示例：

import pandas as pd
from sklearn.linear_model import LinearRegression

# 导入数据
data = pd.read_csv('多元线性回归数据.csv', encoding='gbk')

# 划分特征X和目标Y
X = data[['特征1', '特征2', ...]]
Y = data[['目标Y']]

# 创建并训练模型
model = LinearRegression()
model.fit(X, Y)

# 预测
y_pred = model.predict(X)

# 评估指标
from sklearn.metrics import mean_squared_error, r2_score
mse = mean_squared_error(Y, y_pred)
r2 = r2_score(Y, y_pred)

print(f"均方误差 (MSE): {mse:.2f}")
print(f"决定系数 (R²): {r2:.4f}")

📊 R² 解读：

• R² = 1：完美拟合
• R² = 0：模型不优于"用平均值预测"
• R² < 0：模型比平均值还差

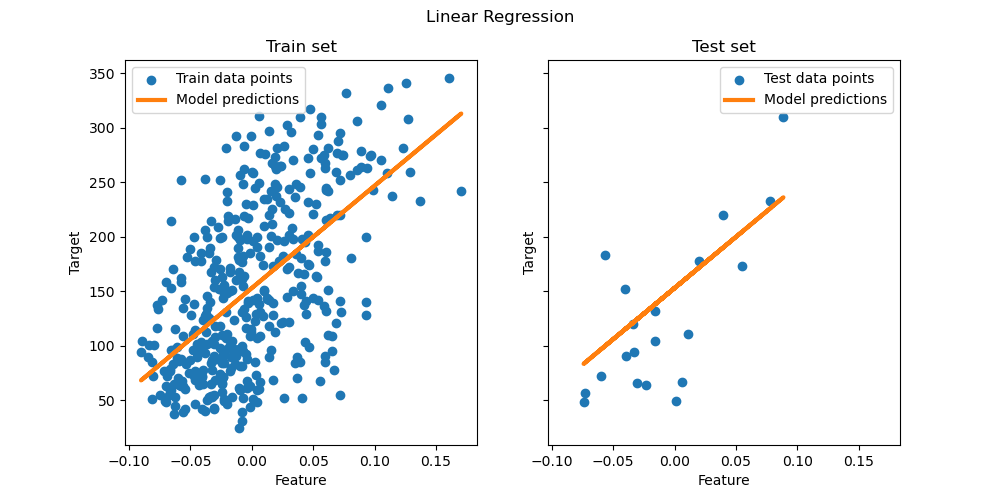
可视化：

import matplotlib.pyplot as plt
# 设置中文字体（避免中文乱码）
plt.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False      # 解决负号显示为方框的问题

# --- 图1：真实值 vs 预测值 ---
plt.figure(figsize=(12, 5))

plt.subplot(1, 2, 1)
plt.scatter(Y, y_pred, alpha=0.7, color='steelblue')
plt.plot([Y.min(), Y.max()], [Y.min(), Y.max()], 'r--', linewidth=2)  # 理想拟合线
plt.xlabel('真实值')
plt.ylabel('预测值')
plt.title(f'真实值 vs 预测值 (R² = {r2:.4f})')
plt.grid(True, linestyle='--', alpha=0.6)

# --- 图2：残差图（Residual Plot）---
residuals = Y - y_pred
plt.subplot(1, 2, 2)
plt.scatter(y_pred, residuals, alpha=0.7, color='darkorange')
plt.axhline(0, color='red', linestyle='--', linewidth=2)
plt.xlabel('预测值')
plt.ylabel('残差 (真实值 - 预测值)')
plt.title('残差图')
plt.grid(True, linestyle='--', alpha=0.6)

# 调整布局并显示
plt.tight_layout()
plt.show()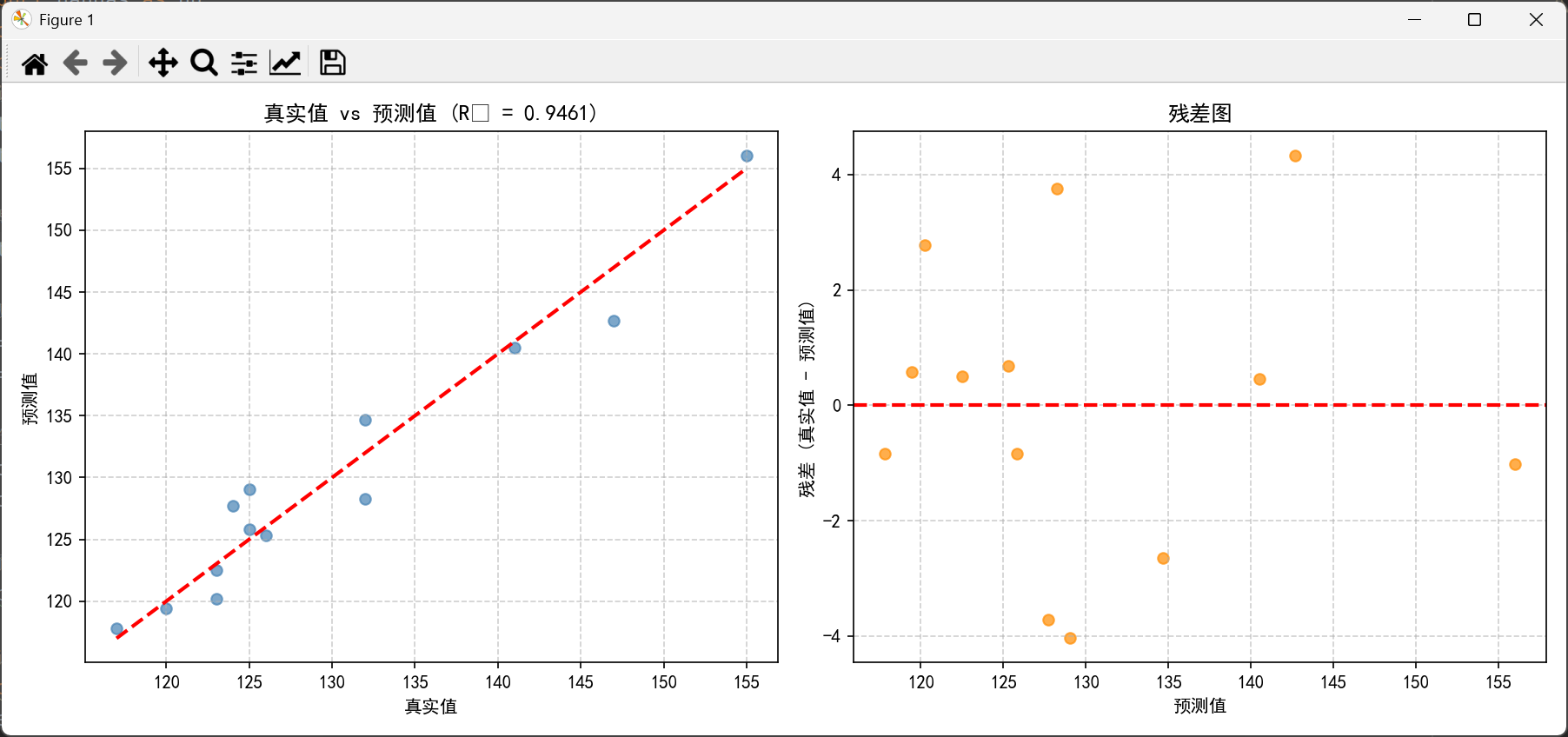

---

二、逻辑回归

1、原理介绍

核心目标

预测离散类别（分类问题） ，尤其是二分类 （如是否患病）。简单一句话来说，逻辑回归就是用来分类的。

基本思想

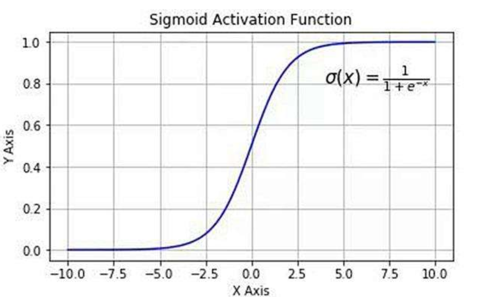
虽然叫"回归"，但本质是分类算法 ！它先用线性模型计算一个"得分"，再通过 Sigmoid 函数 将其映射到 0～1 的概率。

数学模型

1.先计算线性组合：

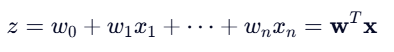
2.再通过 Sigmoid 函数得到概率：

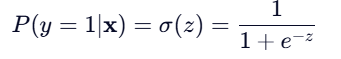
3.最终分类决策

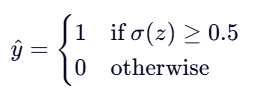
分类效果如下面图形所示：

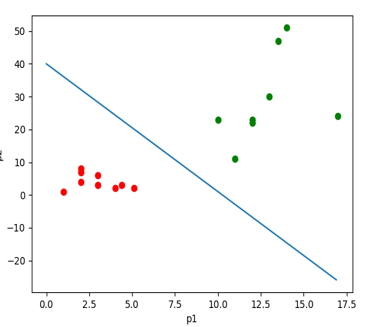
Sigmoid 函数将线性决策边界（直线）两侧的原始线性得分 z，转换为 (0, 1) 区间内的"属于正类的概率"。

• 直线一侧（ z>0 ） → 转换为 大于 0.5 的概率（越远离直线，概率越接近 1）
• 直线另一侧（ z<0 ） → 转换为 小于 0.5 的概率（越远离直线，概率越接近 0）
• 恰好在直线上（ z=0 ） → 概率为 0.5

2、实战代码示例：

任务目标

根据肿瘤大小（size）判断是否为恶性（malignant: 0=良性, 1=恶性）

---

导入库 & 设置

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# 设置中文字体（避免中文乱码）
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

步骤 1：生成分类数据

# 模拟医疗数据
np.random.seed(42)
size_benign = np.random.normal(10, 2, 80)    # 良性：均值10
size_malignant = np.random.normal(18, 3, 70) # 恶性：均值18

# 合并数据
size = np.concatenate([size_benign, size_malignant])
label = np.concatenate([np.zeros(80), np.ones(70)])  # 0=良性, 1=恶性

df = pd.DataFrame({'size': size, 'malignant': label})
print(df.head())

---

步骤 2：准备数据

X = df[['size']]
y = df['malignant']

---

步骤 3：划分数据集

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.25, random_state=42, stratify=y  # 保持类别比例
)

💡 stratify=y：确保训练/测试集中良恶性比例一致

---

步骤 4：训练逻辑回归模型

from sklearn.linear_model import LogisticRegression

model = LogisticRegression()
model.fit(X_train, y_train)

🔍 注意：逻辑回归默认使用 L2 正则化 ，可通过 penalty='none' 关闭

---

步骤 5：预测概率与类别

# 预测概率（属于恶性 class=1 的概率）
y_prob = model.predict_proba(X_test)[:, 1]

# 预测类别（默认阈值 0.5）
y_pred = model.predict(X_test)

print("前5个样本的恶性概率:", y_prob[:5].round(3))
print("前5个预测类别:", y_pred[:5])

💡 输出示例：
恶性概率: [0.021 0.987 0.005 0.992 0.876]
预测类别: [0 1 0 1 1]

---

步骤 6：评估分类效果

from sklearn.metrics import accuracy_score, classification_report, confusion_matrix

acc = accuracy_score(y_test, y_pred)
print(f"准确率: {acc:.4f}")
print("\n分类报告:")
print(classification_report(y_test, y_pred, target_names=['良性', '恶性']))

# 混淆矩阵
cm = confusion_matrix(y_test, y_pred)
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues',
            xticklabels=['良性', '恶性'],
            yticklabels=['良性', '恶性'])
plt.title('混淆矩阵')
plt.ylabel('真实标签')
plt.xlabel('预测标签')
plt.show()

📊 关键指标：

• 准确率（Accuracy）：整体正确率
• 精确率（Precision）：预测为恶性中，真恶性的比例
• 召回率（Recall）：所有真恶性中，被找出来的比例

---

步骤 7：可视化决策边界

# 生成平滑曲线
x_plot = np.linspace(X.min(), X.max(), 300).reshape(-1, 1)
prob_plot = model.predict_proba(x_plot)[:, 1]

plt.figure(figsize=(8, 5))
plt.scatter(X[y==0], y[y==0], color='green', label='良性', alpha=0.6)
plt.scatter(X[y==1], y[y==1], color='red', label='恶性', alpha=0.6)
plt.plot(x_plot, prob_plot, color='blue', linewidth=2, label='Sigmoid 概率曲线')
plt.axhline(0.5, color='gray', linestyle='--', linewidth=1)  # 阈值线
plt.axvline(-model.intercept_[0]/model.coef_[0][0], color='purple', linestyle=':', label='决策边界')
plt.xlabel('肿瘤大小')
plt.ylabel('恶性概率')
plt.title('逻辑回归：肿瘤分类')
plt.legend()
plt.show()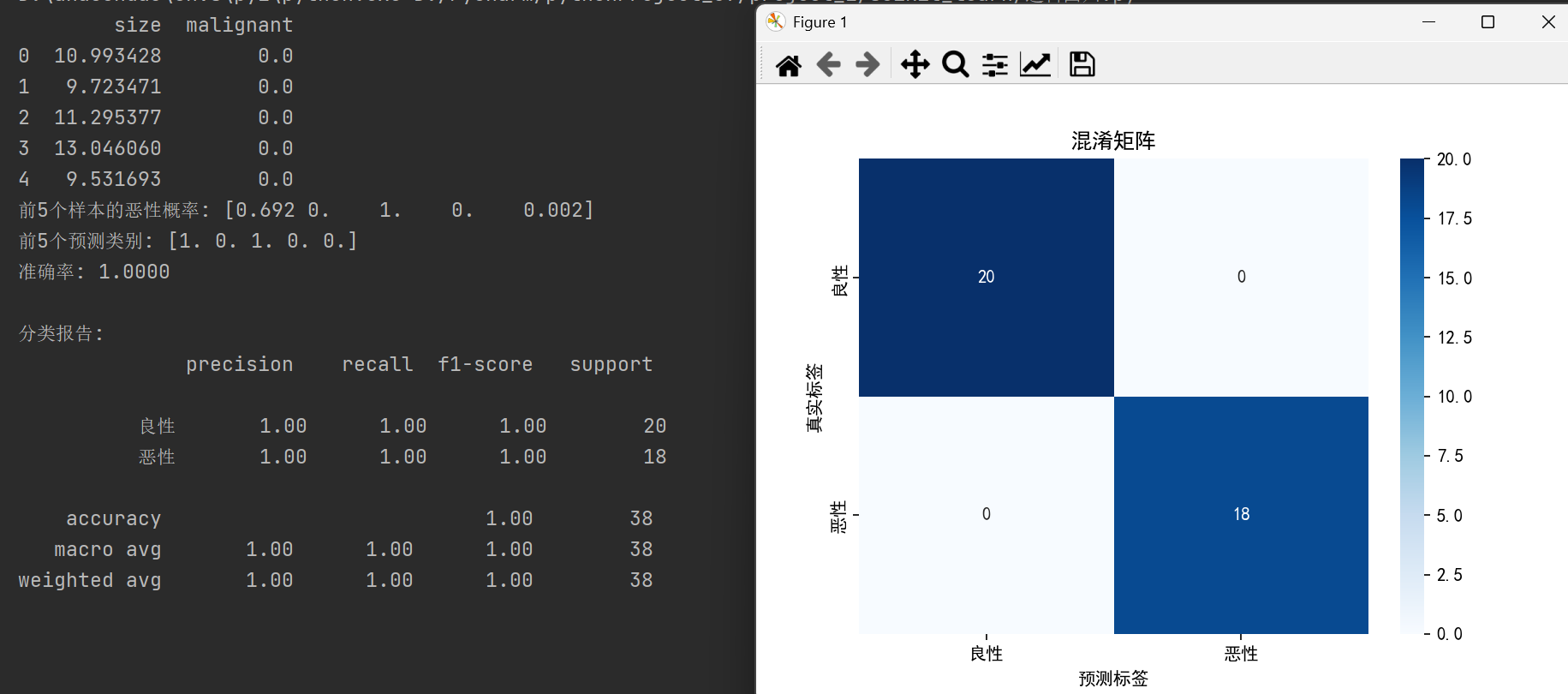

图中：

• 蓝线：Sigmoid 概率曲线
• 紫线：决策边界（概率=0.5 对应的 size 值）
• 灰线：概率 0.5 阈值

---

🔚 总结对比

项目	线性回归	逻辑回归
任务	回归（预测连续值）	分类（预测离散标签）
输出	实数（如 50.3）	概率（0～1）→ 转为 0/1
核心函数	无（直接输出）	Sigmoid
损失函数	MSE	Log Loss
评估指标	R², MSE	准确率, 精确率, 召回率
sklearn 类	LinearRegression	LogisticRegression