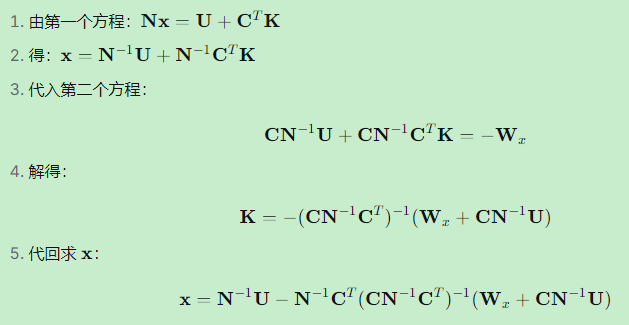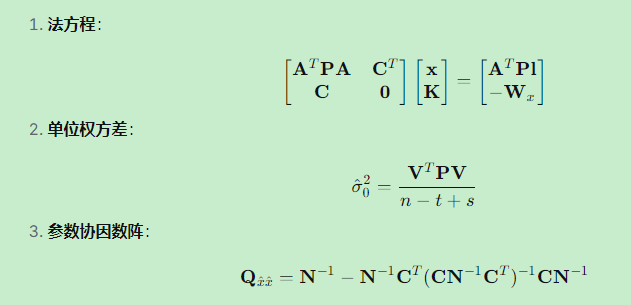附有限制条件的间接平差原理详解
一、基本思想与特点
附有限制条件的间接平差是间接平差的重要扩展,它解决了一类特殊问题:
在参数估计过程中,未知参数本身还存在约束关系(如几何条件、物理条件等),需要将这些约束条件融入平差模型。
特点:
-
参数存在约束:未知参数不完全独立,存在数学或物理约束
-
双重优化:既要最小化观测值残差,又要满足参数约束
-
应用广泛:在控制网平差、工程测量、GNSS数据处理中常见
典型应用场景:
-
已知某些边长或方位角的控制网平差
-
GNSS网中已知基线长度或坐标差的约束
-
变形监测中已知某些点之间的几何关系
-
工业测量中已知部件尺寸约束
二、数学模型
2.1 观测方程(与间接平差相同)

2.2 参数限制条件方程

三、最小二乘准则与求解
3.1 拉格朗日函数构造

3.2 求偏导并令为零
3.3 法方程

3.4 法方程求解
方法一:直接求逆法

方法二:消元法(更常用)
3.5 参数估值与平差值
四、精度评定
4.1 单位权方差估值

4.2 参数的协因数阵

4.3 参数估值的中误差

4.4 平差值 L^ 的协因数阵
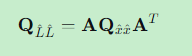
4.5 参数函数的精度评定

五、计算步骤
六、示例:水准网附有限制条件的间接平差
6.1 问题描述
水准网中,已知A点高程 H_A = 10.000mHA=10.000m,观测了3条路线的高差:
-
路线1:A→B,h_1 = +2.500mh1=+2.500m,路线长 S_1 = 2kmS1=2km
-
路线2:B→C,h_2 = +1.000mh2=+1.000m,路线长 S_2 = 1kmS2=1km
-
路线3:A→C,h_3 = +3.498mh3=+3.498m,路线长 S_3 = 3kmS3=3km
附加限制条件:已知B、C两点的高差为 1.000m1.000m(即 H_C - H_B = 1.000mHC−HB=1.000m),将此条件作为限制条件。
6.2 平差计算



步骤7:解法方程 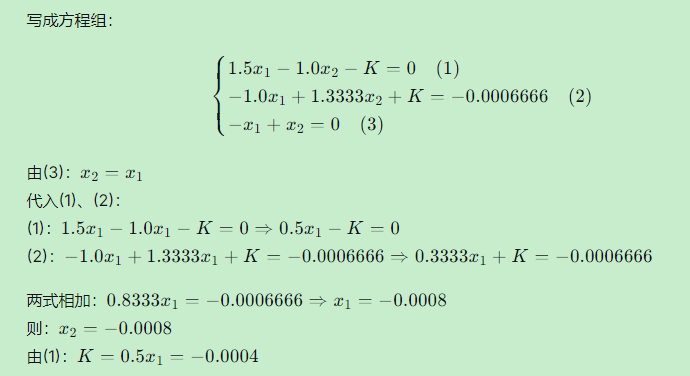
步骤8:计算平差值 
步骤9:精度评定
-
单位权方差:

-
参数协因数阵:
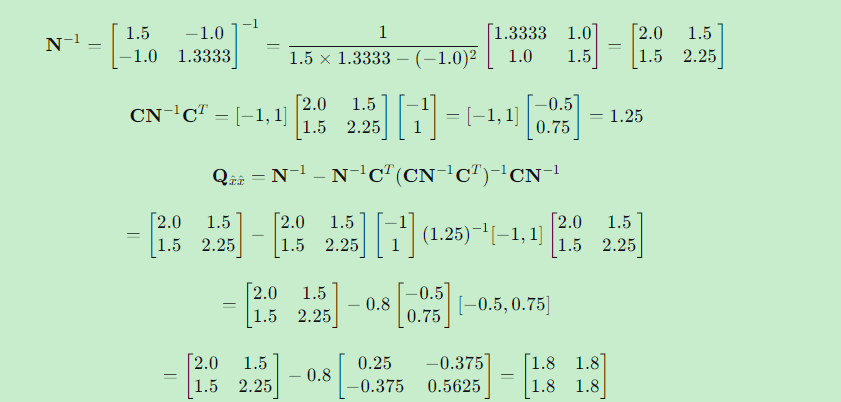
-
参数中误差:
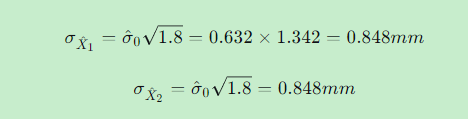
七、与其它平差方法的比较
7.1 与间接平差的关系
当 s=0s=0(无限制条件)时,附有限制条件的间接平差退化为间接平差。
7.2 与条件平差的关系
可以通过消元法将附有限制条件的间接平差转化为条件平差。
7.3 与附有参数的条件平差的关系
两者在数学上等价,只是出发点和未知数选择不同。
八、在AGNSS中的应用
8.1 GNSS网平差中的约束
在GNSS网平差中,常有以下约束:
-
已知坐标约束:某些点坐标已知或部分已知
-
已知基线约束:某些基线长度或方位已知
-
已知高差约束:某些点高差已知
-
系统间约束:不同GNSS系统间的转换参数约束
8.2 示例:GNSS基线向量网平差
设有GNSS基线向量观测值,部分点坐标已知,部分基线长度已知。
模型:
-
观测方程:基线向量观测值
-
限制条件:
-
已知点坐标约束
-
已知基线长度约束
-
处理:
-
将所有点坐标设为参数
-
已知点坐标作为约束条件
-
已知基线长度作为非线性约束,需要线性化
8.3 多系统GNSS融合中的约束
不同GNSS系统间可能存在系统偏差,这些偏差可作为参数并施加约束。
九、关键问题与注意事项
9.1 限制条件的线性化
非线性约束需要线性化,线性化点的选择影响收敛性。
9.2 限制条件的独立性
限制条件必须是独立的,否则法方程系数矩阵奇异。
9.3 病态问题处理
当限制条件与观测方程强相关时,法方程可能病态,需要正则化处理。
9.4 计算效率
参数多时,直接求逆计算量大,可采用消元法或迭代法。
十、总结
10.1 核心思想
将参数约束条件融入间接平差框架,实现带约束的参数估计。
10.2 关键公式
10.3 应用价值
-
充分利用先验信息:将已知条件作为约束,提高解算精度
-
统一处理各类问题:可处理坐标约束、几何约束、物理约束等
-
提高成果可靠性:约束条件可增强网形的强度
附有限制条件的间接平差是测量数据处理的重要工具,掌握其原理对解决复杂工程问题至关重要。
笔记: