【MATLAB程序】Dubins曲线，车辆轨迹规划，给定起终点、半径和朝向，得到路径输出（绘图）和运动组合。附代码下载链接

基于Dubins曲线的车辆轨迹规划例程，已经设置好了起终点等参数，直接运行即可得到结果，也可根据例子来修改成自己需要的数值

文章目录

核心算法原理
主要函数说明
运行结果
MATLAB源代码

核心算法原理

Dubins曲线由三种基本运动组成：

L (Left): 左转弧线
S (Straight): 直线段
R (Right): 右转弧线

可能的6种组合方式：LSL, LSR, RSL, RSR, RLR, LRL

主要函数说明

dubins_core - 核心计算函数

matlab 复制代码

% 关键步骤：
% 1. 归一化距离和角度
% 2. 枚举6种路径组合
% 3. 选择总长度最短的方案

计算过程：

将起点到终点的距离归一化（除以转弯半径）
计算相对航向角 α 和 β
对6种路径类型分别求解
返回最优路径参数

6种路径求解函数
每种函数使用几何关系求解三段路径的长度参数(t, p, q)：

dubins_LSL/RSR: 两个同向圆弧+直线
dubins_LSR/RSL: 两个异向圆弧+直线
dubins_RLR/LRL: 三段圆弧

关键：通过 p_squared 判断路径是否可行（必须≥0）

dubins_path_sample - 路径采样
根据弧长参数 t，计算路径上对应点的位置和朝向：

matlab 复制代码

% 分三段处理：
% - 判断t属于哪一段
% - 调用dubins_segment计算局部坐标
% - 转换回世界坐标系

dubins_segment - 单段计算
计算单个路段的终点位姿：

L_SEG: 左转圆弧运动
R_SEG: 右转圆弧运动
S_SEG: 直线运动

运行结果

设定起终点及朝向数据：

matlab 复制代码

pointA = [ 1, 2,   100*pi/180 ]; % 起点位姿（X, Y, 朝向rad）
pointB = [ 10, 2, 120*pi/180 ]; % 终点位姿（X, Y, 朝向rad）

设定最小转弯半径：

matlab 复制代码

TurnRadius = 1; % 最小转弯半径

得到的轨迹图：

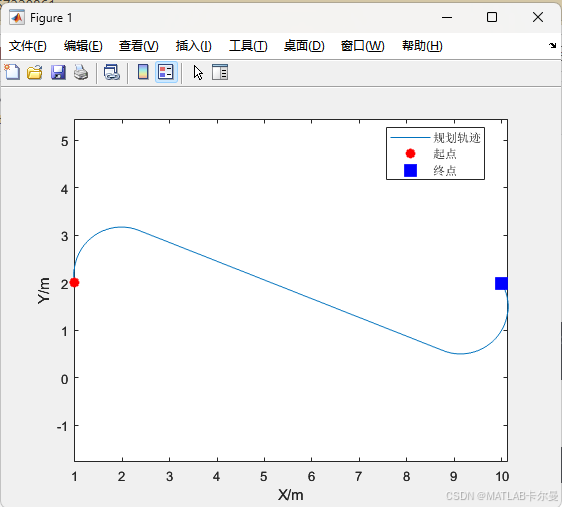
得到的命令行输出：

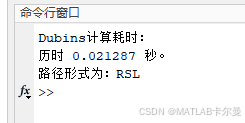
如果把转弯半径修改为10，则：

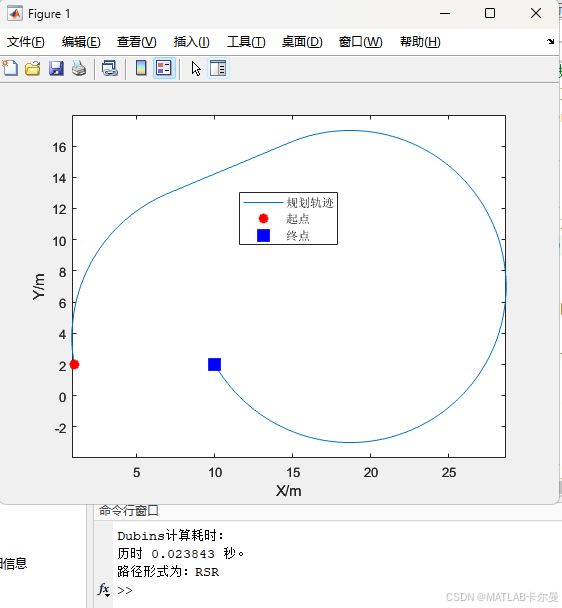
MATLAB源代码

部分代码如下：

matlab 复制代码

% 基于Dubins曲线的车辆轨迹规划例程
% 作者:matlabfilter
% 2026-01-21/Ver1

clc;clear;close all;
rng(0);
pointA = [ 1, 2,   100*pi/180 ]; % 起点位姿（X, Y, 朝向rad）
pointB = [ 10, 2, 120*pi/180 ]; % 终点位姿（X, Y, 朝向rad）
TurnRadius = 10; % 最小转弯半径
PathStep = -1;  % 步长（若小于0则自动计算）

[path_out] = dubins_curve(pointA, pointB, TurnRadius);

% --- 绘图部分 ---
figure;
plot(path_out(:,1), path_out(:,2), 'DisplayName', '规划轨迹');
axis equal;
hold on
plot(path_out(1,1), path_out(1,2), '*r', 'LineWidth', 5, 'DisplayName', '起点');
plot(path_out(end,1), path_out(end,2), 'sb', 'LineWidth', 5, 'DisplayName', '终点');
legend('Location', 'best');
xlabel('X/m'); ylabel('Y/m');

完整代码：https://download.csdn.net/download/callmeup/92575091

或：
如需帮助，或有导航、定位滤波相关的代码定制需求，请点击下方卡片联系作者