1 简介
随着技术的进步,数值优化问题日益复杂,元启发式逐渐成为应对此类挑战的有效工具。因此,本文提出了一种新颖的元启发式,称为波动光学优化器(WOO)。WOO的灵感来自弗劳恩霍夫衍射实验,该实验揭示了光的波动性质。在WOO中,每个光波对应一个候选解。在优化过程中,解利用光的衍射和干涉效应探索搜索空间,并逐渐向全局最优解(中心亮条纹)移动。
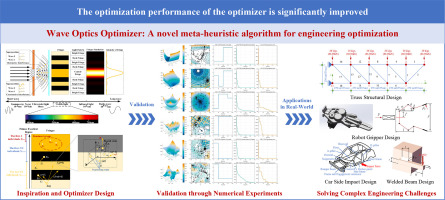
具体而言,衍射效应模拟了光波穿过狭缝的传播特性,增强了初始解的多样性,而干扰效应便于群体之间的交流和学习,引导收敛朝向优越区域。得益于这些特性,WOO能够在复杂的优化环境中高效搜索,同时提高解的稳定性和准确性。
2.灵感
2.1.夫琅和费衍射实验
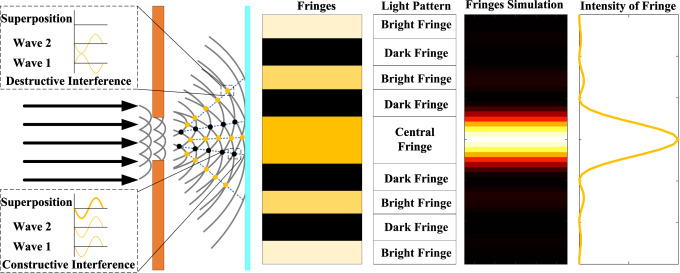
夫琅和费衍射在光学领域占有重要地位[88]、[89]、[90]。本实验描述了光波通过狭缝或圆形孔径等障碍物在屏幕上形成一系列交替的明暗图案的现象。惠更斯-菲涅尔原理对此提供了解释:由于光[91]、[92]的波性质,波阵面上的每一点都可以被认为是新的二次波源,这些二次波向各个方向传播并叠加形成新的波阵面,从而引起衍射。
2.2. 数学模型
2.2.1. 初始种群的生成
与大多数元启发式算法(MHs)类似,在迭代开始之前,WOO需要在优化空间中均匀生成NNN个初始平行光波SiS_iSi,其中SiS_iSi的集合可以形成入射到狭缝上的单色光,如公式(6)和图5所示。同时,在DDD维优化空间中,sijs_i^jsij表示第iii个平行光波SiS_iSi的第jjj个分量,如公式(7)所示。
S=[S1S2⋮Si⋮SN]=[s11s12⋯s1j⋯s1Ds21s22⋯s2j⋯s2D⋮⋮⋱⋮⋱⋮si1si2⋯sij⋯siD⋮⋮⋱⋮⋱⋮sN1sN2⋯sNj⋯sND],{i=1,2,⋯ ,Nj=1,2,⋯ ,DS=\left[\begin{array}{c}S_{1} \\ S_{2} \\ \vdots \\ S_{i} \\ \vdots \\ S_{N}\end{array}\right]=\left[\begin{array}{cccccc}s_{1}^{1} & s_{1}^{2} & \cdots & s_{1}^{j} & \cdots & s_{1}^{D} \\ s_{2}^{1} & s_{2}^{2} & \cdots & s_{2}^{j} & \cdots & s_{2}^{D} \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\ s_{i}^{1} & s_{i}^{2} & \cdots & s_{i}^{j} & \cdots & s_{i}^{D} \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\ s_{N}^{1} & s_{N}^{2} & \cdots & s_{N}^{j} & \cdots & s_{N}^{D}\end{array}\right], \begin{cases}i=1,2, \cdots, N \\ j=1,2, \cdots, D\end{cases}S= S1S2⋮Si⋮SN = s11s21⋮si1⋮sN1s12s22⋮si2⋮sN2⋯⋯⋱⋯⋱⋯s1js2j⋮sij⋮sNj⋯⋯⋱⋯⋱⋯s1Ds2D⋮siD⋮sND ,{i=1,2,⋯,Nj=1,2,⋯,D
sij=r×(Ubj−Lbj)+Lbj(7)s_{i}^{j}=r \times\left(U b^{j}-L b^{j}\right)+L b^{j}\tag{7}sij=r×(Ubj−Lbj)+Lbj(7)
其中UbjU b^{j}Ubj和LbjL b^{j}Lbj是优化空间在第jjj维度的最大值和最小值,也可以被视为第jjj维度的上下界。为了区分后面提到的不同维度中的随机数,rrr被定义为范围[0,1][0,1][0,1]内的一维随机数,而RRR被定义为范围[0,1][0,1][0,1]内的DDD维随机数。
当单色光通过狭缝时,会发生衍射。为了方便后续计算,我们假设衍射后波前上有NNN个点,其中点的数量等于平行光波SiS_iSi的数量。基于公式(1),本文提出了一个计算WOO中平行光波通过狭缝后初始波前位置的模型,如公式(8)至公式(12)所示。
{usi=max(Si)lsi=min(Si)(8)\begin{cases}u s_{i}=\max \left(S_{i}\right) \\ l s_{i}=\min \left(S_{i}\right)\end{cases}\tag{8}{usi=max(Si)lsi=min(Si)(8)
{sinθ1=0 if i=1md=md+1sinθi=(md+1)×λ2×d if mod (i,2)=0mm=mm+1sinθi=(2×mm+1)×λ2×d else (9)\begin{cases}\sin \theta_{1}=0 & \text { if } \quad i=1 \\ m_{d}=m_{d}+1 \\ \sin \theta_{i}=\frac{\left(m_{d}+1\right) \times \lambda}{2 \times d} & \text { if } \quad \bmod (i, 2)=0 \\ m_{m}=m_{m}+1 \\ \sin \theta_{i}=\frac{\left(2 \times m_{m}+1\right) \times \lambda}{2 \times d} & \text { else }\end{cases} \tag{9}⎩ ⎨ ⎧sinθ1=0md=md+1sinθi=2×d(md+1)×λmm=mm+1sinθi=2×d(2×mm+1)×λ if i=1 if mod(i,2)=0 else (9)
{US1=S1+d×(r×(us1−ls1)+ls1)LS1=S1−d×(r×(us1−ls1)+ls1) if i=1\begin{cases}U S_{1}=S_{1}+d \times\left(r \times\left(u s_{1}-l s_{1}\right)+l s_{1}\right) \\ L S_{1}=S_{1}-d \times\left(r \times\left(u s_{1}-l s_{1}\right)+l s_{1}\right)\end{cases} \text { if } \quad i=1{US1=S1+d×(r×(us1−ls1)+ls1)LS1=S1−d×(r×(us1−ls1)+ls1) if i=1
{USi=Si+d×r×(usi−lsi)+lsiusiLSi=Si−d×r×(usi−lsi)+lsiusi else (10)\begin{cases}U S_{i}=S_{i}+d \times \frac{r \times\left(u s_{i}-l s_{i}\right)+l s_{i}}{u s_{i}} \\ L S_{i}=S_{i}-d \times \frac{r \times\left(u s_{i}-l s_{i}\right)+l s_{i}}{u s_{i}}\end{cases} \text { else } \tag{10}{USi=Si+d×usir×(usi−lsi)+lsiLSi=Si−d×usir×(usi−lsi)+lsi else (10)
ΔSi=d×sinθi(11)\Delta S_{i}=d \times \sin \theta_{i}\tag{11}ΔSi=d×sinθi(11)
Xi=(USi+LSi)2±sign(r1−0.5)×r2×ΔSi(12)X_{i}=\frac{\left(U S_{i}+L S_{i}\right)}{2} \pm \operatorname{sign}\left(r_{1}-0.5\right) \times r_{2} \times \Delta S_{i}\tag{12}Xi=2(USi+LSi)±sign(r1−0.5)×r2×ΔSi(12)
X=[X1X2⋮Xi⋮XN]=[x11x12⋯x1j⋯x1Dx21x22⋯x2j⋯x2D⋮⋮⋱⋮⋱⋮xi1xi2⋯xij⋯xiD⋮⋮⋱⋮⋱⋮xN1xN2⋯xNj⋯xND](13)X=\left[\begin{array}{c}X_{1} \\ X_{2} \\ \vdots \\ X_{i} \\ \vdots \\ X_{N}\end{array}\right]=\left[\begin{array}{cccccc}x_{1}^{1} & x_{1}^{2} & \cdots & x_{1}^{j} & \cdots & x_{1}^{D} \\ x_{2}^{1} & x_{2}^{2} & \cdots & x_{2}^{j} & \cdots & x_{2}^{D} \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\ x_{i}^{1} & x_{i}^{2} & \cdots & x_{i}^{j} & \cdots & x_{i}^{D} \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\ x_{N}^{1} & x_{N}^{2} & \cdots & x_{N}^{j} & \cdots & x_{N}^{D}\end{array}\right]\tag{13}X= X1X2⋮Xi⋮XN = x11x21⋮xi1⋮xN1x12x22⋮xi2⋮xN2⋯⋯⋱⋯⋱⋯x1jx2j⋮xij⋮xNj⋯⋯⋱⋯⋱⋯x1Dx2D⋮xiD⋮xND (13)
F=[F1F2F3⋯FN](14)F=\left[\begin{array}{lllll}F_{1} & F_{2} & F_{3} & \cdots & F_{N}\end{array}\right]\tag{14}F=[F1F2F3⋯FN](14)
在上述方程中,公式(8)用于采样第iii个平行光波SiS_iSi,其中usiu s_{i}usi和lsil s_{i}lsi是SiS_iSi的DDD维分量的最大值和最小值。公式(9)用于计算不同衍射条纹的衍射角。当i=1i=1i=1时,条纹是中央亮条纹,满足θ1=0\theta_{1}=0θ1=0且sinθ1=0\sin \theta_{1}=0sinθ1=0。参数mdm_{d}md和mmm_{m}mm用于区分次级亮条纹和暗条纹的级次。例如,当mm=1m_{m}=1mm=1时,条纹是一级亮条纹。在公式(10)中,USiU S_{i}USi和LSiL S_{i}LSi表示SiS_iSi衍射后生成的新波前的上下界。由于中央亮条纹的衍射角为θ1=0\theta_{1}=0θ1=0,因此US1U S_{1}US1和LS1L S_{1}LS1的计算不需要方向转换,而对于其他条纹,需要使用三角函数调整运动方向。在公式(11)和(12)中,符号函数sign\operatorname{sign}sign和ΔSi\Delta S_{i}ΔSi用于调整XiX_{i}Xi的方向。最后,USiU S_{i}USi、LSiL S_{i}LSi和ΔSi\Delta S_{i}ΔSi用于确定衍射后生成的波XiX_{i}Xi的位置,如公式(12)所示。ΔSi\Delta S_{i}ΔSi由公式(3)中的d×sinθd \times \sin \thetad×sinθ项计算得出,该项表示单缝中不同点光源的光程差,并决定干涉条件。与公式(6)类似,公式(13)中的XXX是存储由衍射生成的NNN个波的位置的集合(也可以称为种群)。公式(14)中的集合FFF存储表示XiX_{i}Xi位置质量的评估值。在最小化问题中,较小的FiF_{i}Fi表示XiX_{i}Xi的位置更好,其中全局最优解被定义为Best X\text{Best } XBest X,其相应的最优适应度值被定义为Best F\text{Best } FBest F。
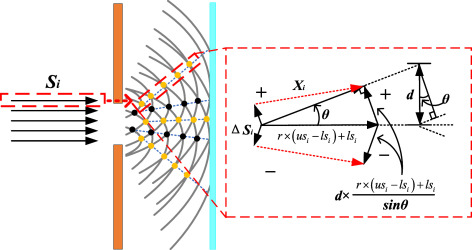
图5. 夫琅禾费衍射的几何模型。
结合基于不确定性原理(UP)的公式(4)和基于德布罗意波(DW)的公式(5),我们可以设计公式(15)。该模型不仅考虑了波粒二象性,还考虑了平行光波在狭缝中可以通过的波前数量。参数UαU \alphaUα表示平行光波通过狭缝时的初始不确定性。在种群初始化期间,每个个体XiX_{i}Xi的扩散不确定性UasiU a s_{i}Uasi被设置为等于UαU \alphaUα,而每个XiX_{i}Xi的扩散影响强度UawiU a w_{i}Uawi被设置为cos(0.5×π×Uα)\cos \left(0.5 \times \pi \times U \alpha\right)cos(0.5×π×Uα)。随后,WOO动态地调整这些值。该策略使WOO能够在整个迭代过程中纳入更真实和动态的解扩散模型。它有助于在解决复杂优化问题时有效引导WOO,防止XiX_{i}Xi陷入局部最优,并确保WOO在复杂搜索空间中保持强大的优化性能。
Ua=λ4×d×2×Nd(15)U a=\frac{\lambda}{4 \times d} \times \frac{2 \times N}{d} \tag{15}Ua=4×dλ×d2×N(15)
在公式(16)中,参数CCC从1递减到0,调节WOO迭代过程中探索和利用之间的平衡。这里,ItI tIt表示当前迭代次数,MaxIt\text{MaxIt}MaxIt表示最大迭代次数。根据屏幕上两波之间的建设性干涉(CI)和破坏性干涉(DI)原理,干涉向量UUU可以使用公式(17)计算。在该方程中,Xr−MidX_{r-M i d}Xr−Mid表示基于适应度排名选择XXX,其中所选个体从排名范围[min(Mid),max(Mid)][\min (M i d), \max (M i d)][min(Mid),max(Mid)]内随机选择。XiX_{i}Xi表示XXX中的第iii个个体。决定种群相互作用范围的矩阵MidM i dMid使用公式(19)计算,并满足Mid∈[1,N]M i d \in[1, N]Mid∈[1,N]。在公式(18)中,TTT用于动态调整种群交互学习能力的强度。在公式(20)中,参数pwp wpw对干涉效应引入扰动。在早期迭代中,pwp wpw提供大的扰动以维持种群多样性。在后期迭代中,它引入较小的扰动以增强局部利用能力。此外,这些小的扰动有助于减轻算子对Best X\text{Best } XBest X周围邻域信息的破坏性影响。
C=1−ItMaxIt(16)C=1-\frac{I t}{\text{MaxIt}}\tag{16}C=1−MaxItIt(16)
U=(Xr−Mid−Xi)×pw(17)U=\left(X_{r-M i d}-X_{i}\right) \times p w\tag{17}U=(Xr−Mid−Xi)×pw(17)
T=∣round((1−sin(π2×Ua))×N)∣(18)T=\left|\operatorname{round}\left(\left(1-\sin \left(\frac{\pi}{2} \times U a\right)\right) \times N\right)\right| \tag{18}T= round((1−sin(2π×Ua))×N) (18)
Mid=[T+1,round(N−12×Ua2×C×T)](19)\text{Mid}=\left[T+1, \text{round}\left(N-\frac{1}{2 \times U a^{2}} \times C \times T\right)\right]\tag{19}Mid=[T+1,round(N−2×Ua21×C×T)](19)
pw=sin((−eIt+1)×π2)(20)p w=\sin \left(\left(-e^{I t}+1\right) \times \frac{\pi}{2}\right)\tag{20}pw=sin((−eIt+1)×2π)(20)
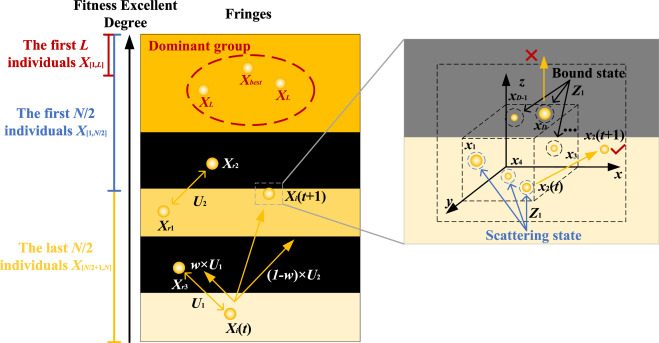
WOO中个体的选择策略如公式(21)所示,其中U2U_{2}U2是引导波XiX_{i}Xi在屏幕上扩散的学习向量。XiX_{i}Xi由从XXX中随机选择的两个个体引导:Xr1−N/2X_{r 1-N / 2}Xr1−N/2表示从FFF中排名前N/2N / 2N/2的个体中随机选择的个体,而Xr2−N/2+1X_{r 2-N / 2+1}Xr2−N/2+1表示从FFF中排名后N/2N / 2N/2的个体中随机选择的个体。此外,Xr2X_{r 2}Xr2和Xr3X_{r 3}Xr3指从XXX中随机选择的两个个体。在迭代的早期阶段,为了在搜索空间中获得更多的位置信息,XiX_{i}Xi需要广泛利用从XXX中随机选择的个体来调整其位置。在迭代的中后期,由于种群已经获取了一定量的空间信息,它逐渐转向利用有前景的位置以获得更高质量的解。在这个阶段,WOO基于FFF的质量对XXX进行排名,因为排名前N/2N / 2N/2的个体更接近全局最优位置,使它们成为个体扩散的合适参考。
U2={Xr1−N/2−Xr2, if i<N2 and rand>CXr1−N/2−Xr1−N/2+1, if i≥N2 and rand>CXr2−Xr3, else (21)U_{2}=\begin{cases}X_{r 1-N / 2}-X_{r 2}, & \text { if } \quad i<\frac{N}{2} \quad \text { and } \quad \text{rand}>C \\ X_{r 1-N / 2}-X_{r 1-N / 2+1}, & \text { if } \quad i \geq \frac{N}{2} \quad \text { and } \quad \text{rand}>C \\ X_{r 2}-X_{r 3}, & \text { else }\end{cases}\tag{21}U2=⎩ ⎨ ⎧Xr1−N/2−Xr2,Xr1−N/2−Xr1−N/2+1,Xr2−Xr3, if i<2N and rand>C if i≥2N and rand>C else (21)
WOO中U1U_{1}U1、U2U_{2}U2的选择方法和更新策略由公式(22)和(23)调节。τ1\tau_{1}τ1是平滑过渡的调节参数,而τ2\tau_{2}τ2是经过指数增强后导致更剧烈变化趋势的调节参数。当τ2>rand\tau_{2}>\text{rand}τ2>rand时,执行第2.2.2节中的随机策略,主要侧重于探索;否则,执行第2.2.3节中的强化策略,主要侧重于利用。
τ1=I0×(0.2×C+0.8)(22)\tau_{1}=I_{0} \times(0.2 \times C+0.8) \tag{22}τ1=I0×(0.2×C+0.8)(22)
τ2=eτ1(23)\tau_{2}=e^{\tau_{1}}\tag{23}τ2=eτ1(23)
2.2.2. 随机策略
当波在屏幕上相遇并形成交替的明暗条纹时,种群XXX正式进入解空间内的交互学习和搜索阶段。群体向光强最高的位置扩散,该位置记为Best X\text{Best } XBest X。为了评估建设性干涉(CI)和破坏性干涉(DI)的效果,可以基于公式(2)和(3)推导计算每个条纹强度的数学模型。在WOO中,这被表述为公式(24)。由于XiX_{i}Xi的分布与FiF_{i}Fi的排名相关,FiF_{i}Fi的排名越高表明XiX_{i}Xi越接近Best X\text{Best } XBest X。类似地,亮条纹越接近中央亮条纹,其强度越强,条纹级次越低。为了确保WOO优先探索和利用高强度区域,本研究引入了一个增强的强度函数ITI_{T}IT,它整合了光强III和种群适应度值FFF,如公式(25)所定义。如果ITI_{T}IT为Inf\text{Inf}Inf或NaN\text{NaN}NaN,则将其设置为1。算法1概述了在WOO中计算光强和条纹级次的步骤。
{I1=I0×sin(π2×C2×(1+C)) if i=1u=π×xλIi=I0×(sinuu)2 else (24)\begin{cases}I_{1}=I_{0} \times \sin \left(\frac{\pi}{2} \times C^{2 \times(1+C)}\right) & \text { if } \quad i=1 \\ u=\pi \times \frac{x}{\lambda} \\ I_{i}=I_{0} \times\left(\frac{\sin u}{u}\right)^{2} & \text { else }\end{cases}\tag{24}⎩ ⎨ ⎧I1=I0×sin(2π×C2×(1+C))u=π×λxIi=I0×(usinu)2 if i=1 else (24)
IT=eIi×Best FFi(25)I_{T}=e^{I_{i} \times \frac{\text{Best } F}{F_{i}}}\tag{25}IT=eIi×FiBest F(25)
Yong Peng, Shaowei Gu, Yunbin Liang, et al, Wave Optics Optimizer: A novel meta-heuristic algorithm for engineering optimization,Communications in Nonlinear Science and Numerical Simulation,Volume 152, Part D,2026,109337, https://doi.org/10.1016/j.cnsns.2025.109337.