数据结构|概念及单向有头链表

一、概念

1.概念

程序 == 数据结构+算法

数据结构：程序操作数据对象的结构

算法：程序操作数据对象的结构

让数据的存储、查找、修改更高效

二、程序效率衡量指标

所有数据结构的设计都是为了平衡时间复杂度和空间复杂度

（1）时间复杂度

数据量增长与程序运行时间增长呈现的比例关系称为时间复杂度函数，简称为时间复杂度；

O(c)、O(logn)、O(n)、O(nlogn)、O(n^2)、O(n^3)...O(2^n)

（2）空间复杂度

数据量增长与程序空间增长呈现的比例函数，简称为空间复杂度

三、数据结构

1.逻辑结构

（1）线性结构：一对一关系；

（2）树形结构：一对多关系；

（3）图形结构：多对多关系。

2.存储结构

（1）顺序存储：优：空间连续，访问元素方便

缺：插入、删除效率低；无法利用小空间。

（2）链式存储：优：插入、删除效率高；可利用小空间；

缺：访问元素不方便，增加额外空间的开销。

（3）索引结构

（4）散列结构

四、数据结构的分类

1.顺序表

本质等同于数组，通过申请堆区空间存储数据，通过首地址完成对所有空间的访问

（1）头文件

seqlist.h

cpp 复制代码

#ifndef __SEQLIST_H__
#define __SEQLIST_H__
typedef int DataType;
extern DataType *CreateSeqlist(int len);
extern void DestorySeqlist(DataType **pparray);
#endif

（2）代码

seqlist.c

cpp 复制代码

#include <stdio.h>
#include <stdlib.h>
#include "seqlist.h"
DataType *CreateSeqlist(int len)
{
        DataType *pret = NULL;
        pret = malloc(len * sizeof(DataType));
        if (NULL == pret)
        {
        perror("fail to malloc");
        return NULL;
        }

        return pret;
}

void DestorySeqlist(DataType **pparray)
{
        free(*pparray);
        *pparray = NULL;
        return;
}

2.链式表

（1）链表分类

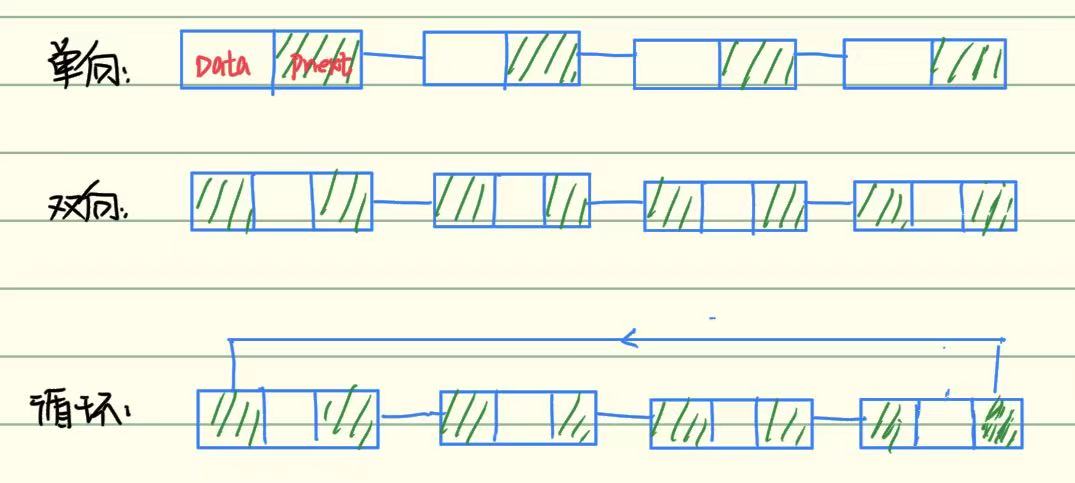
单向链表：

结构：每个节点包含数据域和一个指向下一节点的指针，最后一个节点的指针为 NULL。

特点：只能从头部向尾部单向遍历，查找尾节点需要遍历整个链表。

适用场景：适用于简单的顺序存储、插入删除操作较少的场景。

双向链表：

结构：每个节点包含数据域、前驱指针（指向前一节点）和后继指针（指向后一节点）。

特点：可以双向遍历，但每个节点需要额外存储一个指针，空间开销略大。

适用场景：适用于需要频繁在任意位置插入、删除或双向遍历的场景。

循环链表：

结构：单链表或双链表的基础上，尾节点的指针指向头节点，形成一个闭环。

特点：可以从任意节点开始遍历整个链表，无需担心指针为空。

适用场景：适用于需要循环访问的场景。

3.单向链表

单向链表是基础，我们先来学习单向链表

单向链表分为有头链表和无头链表：

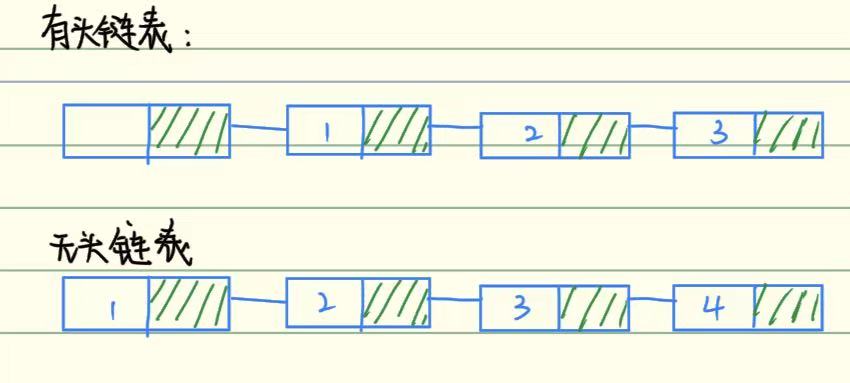
有头链表

结构：链表头部有一个不存储有效数据的哨兵节点，有效节点是哨兵节点的后继；链表为空时，哨兵节点的pNext为NULL。

1.有头链表的创建

（1）首先先创建哨兵节点:

cpp 复制代码

typedef int TypeDate;    


typedef struct node
{
    TypeDate Date;
    struct node *pNext;
}Node_t;

Node_t *pNewNode = NULL;

pNewNode = malloc(sizeof(Node_t));
if(NULL == pNewNode)
{
     perror("failed to malloc");
     return NULL;
}

pNewNode->pNext = NULL;

（2）再进行以下步骤创建单向有头链表：

申请节点空间；
存放数据到节点的Data；
将pNext赋值为空白节点的pNext;
将空白节点的pNext赋值为新申请的节点。

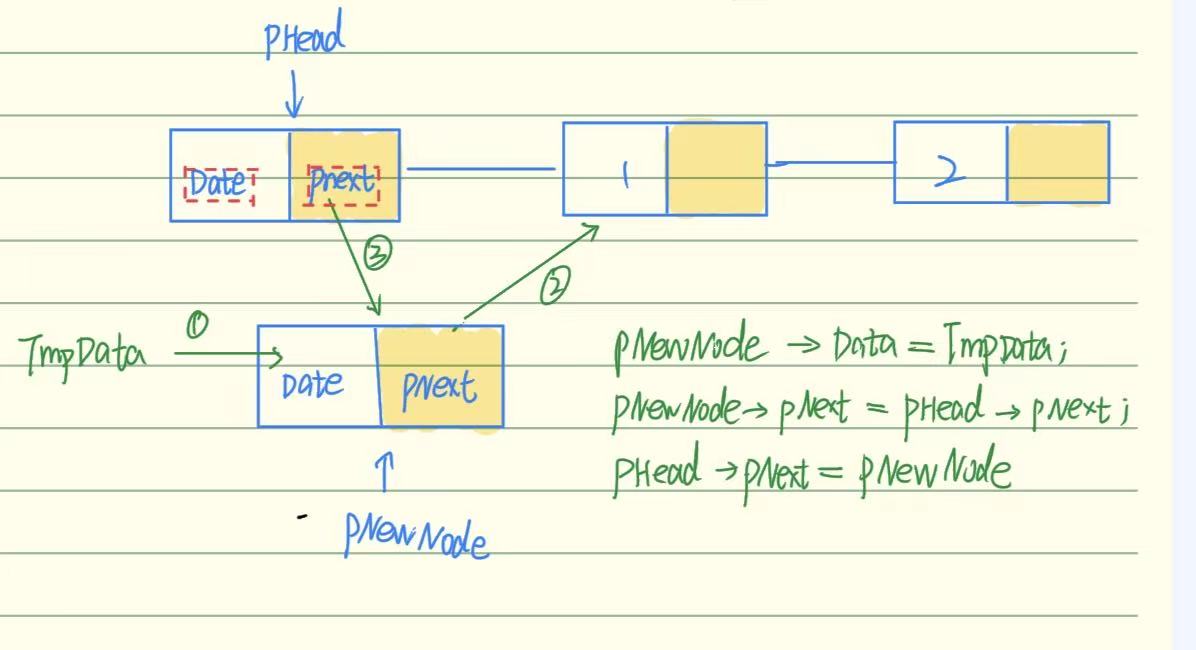
拓展：尾插法

在链表最后一个节点的后面插入新节点，插入后新节点成为新的尾节点

遍历链表找到尾节点（判断节点的next == NULL）；
将尾节点的next指向新节点；
将新节点的next置为NULL，成为新尾节点。

示例：

cpp 复制代码

#include<stdio.h>
#include<stdlib.h>

typedef int DataType;

typedef struct node
{
    DataType Data;
    struct node *pNext;
}Node_t;

Node_t *CreatEmpty(void)
{
    Node_t *pNewNode = NULL;
    pNewNode = malloc(sizeof(Node_t));
    if(NULL == pNewNode)
    {
        perror("fail to malloc");
        return NULL;
    }
    pNewNode->pNext = NULL;

    return pNewNode;
}

int InsertTailLinkNode(Node_t *pHead, DataType TmpData)
{
    Node_t *pNewNode = NULL;
    Node_t *pTail = NULL;

    pNewNode = malloc(sizeof(Node_t));
    if(NULL == pNewNode)
    {
        perror("fail to malloc");
        return -1;
    }  
    
    pNewNode->Data = TmpData;
    pNewNode->pNext = NULL;

    pTail = pHead;
    while(pTail->pNext != NULL)
    {
        pTail = pTail->pNext;
    }

    pTail->pNext = pNewNode;

    return 0;
}

void ShowLinkNode(Node_t *pHead)
{
    Node_t *pTmpNode = NULL;

    pTmpNode = pHead->pNext;
    while(NULL != pTmpNode)
    {
        printf("%d ",pTmpNode->Data);
        pTmpNode = pTmpNode->pNext;
    }
    printf("\n");

    return;
}

int main(void)
{
    Node_t *plinklist = NULL;

    plinklist = CreatEmpty();

    InsertTailLinkNode(plinklist, 1);
    InsertTailLinkNode(plinklist, 2);
    InsertTailLinkNode(plinklist, 3);
    InsertTailLinkNode(plinklist, 4);
    InsertTailLinkNode(plinklist, 5);

    ShowLinkNode(plinklist);

    return 0;
}

2.链表的遍历

while（p != NULL）

{

p = p->pNext;

}

示例：（打印）

cpp 复制代码

void ShowLinkList(Node_t *pHead)
{
    Node_t *pTmpNode = NULL;

    pTmpNode = pHead->pNext;
    while(pTmpNode != NULL)
    {
        printf("%d ",pTmpNode->Data);
        pTmpNode = pTmpNode->pNext;
    }
    printf("\n");

    return;
}

3.找链表最后一个节点

while（p->pNext != NULL）

{

p = p->pNext;

}

示例：

cpp 复制代码

 pTail = pHead;
    while(pTail->pNext != NULL)
    {
        pTail = pTail->pNext;
    }

3.链表节点的删除

（1）定义两个指针，一个指针空白节点，一个指向第一个有效节点；

（2）循环遍历所有节点，判断ptmp指向的是否为要删除的节点；

（3）找到要删除的节点后，将pPre->pNext赋为ptmp->pNext;

（4）释放要删除的节点；

（5）将ptmp指向下一个判断的节点。

示例：（部分代码）

cpp 复制代码

typedef int TypeDate;    


typedef struct node
{
    TypeDate Date;
    struct node *pNext;
}Node_t;

int DeleteLinkNode(Node_t *pHead, DataType TmpData)
{
    int cnt = 0;
    Node_t *pPreNode = NULL;
    Node_t *pTmpNode = NULL;

    pPreNode = pHead;
    pTmpNode = pHead->pNext;

    while(pTmpNode != NULL)
    {
        if(pTmpNode->Data == TmpData)
        {
           pPreNode->pNext = pTmpNode->pNext;
           free(pTmpNode);
           pTmpNode = pPreNode->pNext;
           cnt++;
        }
        else
        {
            pPreNode = pPreNode->pNext;
            pTmpNode = pTmpNode->pNext;
        }
    }