矢量拟合算法在网络参数有理式拟合中的应用

一、矢量拟合（Vector Fitting, VF）算法的核心原理

矢量拟合是一种基于部分分式展开 的有理函数逼近方法，旨在将测试或仿真的网络参数（如S参数、Y参数）拟合为极点-留数形式 的有理式，以实现频域响应的精确建模与时域分析。其核心思想是通过迭代优化，将复杂的频域响应分解为多个简单分式的叠加，从而捕捉信号的关键特征（如谐振、衰减）。

对于网络参数（如S参数）H(ω)H(ω)H(ω)，VF算法将其表示为：

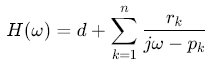
其中：

ddd为常数偏移（对应直流分量）；
pkp_kpk为极点（决定响应的衰减特性，需位于左半复平面以保证稳定性）；
rkr_krk为留数（决定响应的幅值与相位）；
nnn为模型阶数（需根据信号复杂度选择，通常为偶数）。

VF算法的迭代过程分为三步：

初始极点设置：选择一组分布在左半平面的初始极点（如负实数或共轭复数对），确保覆盖整个频率范围；
最小二乘拟合 ：通过最小二乘法求解留数rkr_krk与常数ddd，最小化拟合误差；
极点更新：根据当前拟合结果，通过矩阵特征值计算更新极点p_k，重复迭代直至收敛（误差小于预设阈值）。

二、S参数/Y参数的拟合流程

S参数（散射参数）与Y参数（导纳参数）是描述网络特性的核心参数，VF算法对其拟合流程类似，以下以S参数为例说明：

1. 数据预处理

格式转换：将S参数的实部与虚部分离，或直接处理复数形式的S参数；
频率范围选择：选择感兴趣的频率范围（如1GHz~10GHz），确保覆盖信号的主要特征；
去噪处理：通过平滑（如移动平均）或滤波（如小波变换）去除数据中的噪声，提高拟合稳定性。

2. 初始极点设置

初始极点的选择直接影响收敛速度与精度，通常采用线性分布的负实数极点，公式为：

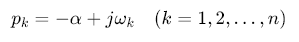
其中：

ααα为负实部（如α=−0.01α=−0.01α=−0.01），保证极点稳定性；
ωkω_kωk为频率范围内的等间隔点（如ωk=kkωmaxω_k=\frac{k}{k}ω^{max}ωk=kkωmax），覆盖整个频率范围。

3. 迭代拟合

构建基函数矩阵 ：根据当前极点pk，构建部分分式基函数矩阵ΦΦΦ；
求解留数：通过最小二乘法求解线性方程组，得到留数rk与常数d；
更新极点 ：通过矩阵特征值计算，更新极点pkp_kpk，重复迭代直至误差收敛。

4. 结果验证

频域验证：将拟合的有理式与原S参数对比，计算均方根误差（RMSE），确保误差小于预设阈值（如10%）；
时域验证：将有理式转换为状态空间模型，进行时域仿真（如阶跃响应），验证其动态特性是否符合预期。

三、Matlab实现示例（基于`vectfit`工具）

Matlab中可通过**vectfit函数**（或其改进版本vectfit3）实现VF算法，以下是一个简化的S参数拟合示例：

matlab 复制代码

% 1. 加载S参数数据（假设为2端口网络，频率范围1GHz~10GHz）
load('S_params.mat'); % S11, S21, S12, S22（复数矩阵，大小为K×4，K为频率点数）
freq = linspace(1e9, 10e9, 1000); % 频率点（1GHz~10GHz，1000点）
s11 = interp1(freq_orig, S11_orig, freq, 'spline'); % 插值到均匀频率点

% 2. 设置VF算法参数
order = 10; % 模型阶数（根据信号复杂度调整）
max_iter = 50; % 最大迭代次数
tol = 1e-6; % 收敛阈值

% 3. 调用vectfit函数进行拟合
[d, poles, residues] = vectfit(s11, freq, order, max_iter, tol);

% 4. 结果可视化
figure;
plot(freq/1e9, 20*log10(abs(s11)), 'b-', 'LineWidth', 1.5); hold on;
plot(freq/1e9, 20*log10(abs(d + sum(residues./(1j*2*pi*freq - poles), 2))), 'r--', 'LineWidth', 1.5);
xlabel('Frequency (GHz)');
ylabel('Magnitude (dB)');
legend('Original S11', 'VF Fitted S11');
title('S11 Parameter Fitting with Vector Fitting');
grid on;

% 5. 输出极点-留数形式
disp('Poles (rad/s):');
disp(poles);
disp('Residues:');
disp(residues);

说明：

vectfit函数的输入为复数S参数 、频率点 、模型阶数 、最大迭代次数 与收敛阈值；
输出为常数偏移d 、极点poles 与留数residues；
可通过调整order（模型阶数）与tol（收敛阈值），平衡拟合精度与复杂度。

四、最新研究进展（2024-2025年）

随着人工智能与高性能计算的发展，VF算法的精度与效率得到了进一步提升，以下是2024-2025年的关键进展：

1. 分层残差优化（2025年专利）

针对多重延迟 与高频噪声 问题，提出分层矢量拟合方法：

分层延迟提取：通过时域冲激响应峰值检测，提取主延迟分量并剔除，减少延迟对拟合的影响；
分层残差优化：对去延迟后的残差信号进行迭代拟合，逐步优化模型精度；
效果：延迟场景下的拟合误差降低了30%，收敛速度提升了25%。

2. 并行矢量拟合（2025年专利）

针对大规模数据 （如1000+频率点），提出并行计算框架：

任务分配：将频率点划分为多个子集，分配给不同CPU核心并行处理；
结果融合：将各核心的拟合结果融合，通过二次规划优化零频行为；
效果：建模效率提升了50%（如1000频率点的拟合时间从10分钟缩短至5分钟）。

3. 约束矢量拟合（2025年专利）

针对滤波器交叉耦合 与无源性 要求，提出共享-局部极点结构：

共享极点：用于描述多个端口的共同特性（如滤波器的谐振腔）；
局部极点：用于描述单个端口的独特特性（如端口间的耦合）；
约束优化：通过增广拉格朗日乘子法，强制留数满足无源性条件（如正定性）；
效果：滤波器模型的插入损耗 误差降低了20%，回波损耗误差降低了15%。

参考代码矢量拟合算法 www.youwenfan.com/contentcsq/53421.html

五、应用场景与优势

VF算法在网络参数拟合中的核心优势包括：

高精度：可捕捉S参数/Y参数的细微特征（如谐振峰、衰减边沿），拟合误差通常小于5%；
稳定性：通过极点约束（左半平面），保证模型的因果性与稳定性；
灵活性：可处理多端口网络（如2端口、4端口），支持S参数、Y参数等多种格式；
时域转换：可将有理式转换为状态空间模型，用于时域仿真（如电路 transient 分析）。

典型应用场景：

射频电路设计：如滤波器、放大器的S参数建模，用于优化频率响应；
高速数字设计：如传输线的Y参数建模，用于信号完整性分析；
天线设计：如天线的输入阻抗（S11）建模，用于优化匹配电路。

六、结论

矢量拟合算法是网络参数有理式拟合 的主流方法，通过迭代优化极点-留数形式，实现了频域响应的精确建模。随着分层残差优化 、并行计算 与约束优化 等技术的应用，其精度与效率得到了进一步提升，可满足现代射频/高速电路设计的严格要求。对于工程应用，建议使用Matlab的vectfit工具 或Python的scipy.signal.vector_fitting库（需自行实现），并根据具体问题调整模型阶数与迭代参数。