文章目录
交换排序
理论
冒泡排序
冒泡排序是一种简单的排序算法,它重复地走访要排序的数列,一次比较两个相邻元素,如果它们的顺序错误就交换位置,直到没有需要交换的元素为止。
水里面的泡泡往上浮的感觉
假设对数组 [64, 34, 25, 12, 22, 11, 90] 排序:
每轮发现一个最大值,第一次遍历下标[0,n-2],第二次遍历下标[0,n-3],n-1轮够了
第一轮冒泡:
- 64 > 34,交换 → [34, 64, 25, 12, 22, 11, 90]
- 64 > 25,交换 → [34, 25, 64, 12, 22, 11, 90]
- 64 > 12,交换 → [34, 25, 12, 64, 22, 11, 90]
- 64 > 22,交换 → [34, 25, 12, 22, 64, 11, 90]
- 64 > 11,交换 → [34, 25, 12, 22, 11, 64, 90]
- 64 < 90,不交换
第一轮结束后,90已就位
后续轮次继续类似过程...
第一次优化
某一轮后,整个元素数组有序了
第二次优化
循环多少轮,是由冒泡过程最后的交换的索引号尾依据
引入变量记录最后一次交换的位置
tex
原始数组: [5, 3, 8, 2, 1, 4]
第1轮 (n=6):最大值
比较: [5,3,8,2,1,4]
↑ 交换 → [3,5,8,2,1,4] newIndex=1
↑ 保持 → [3,5,8,2,1,4]
↑ 交换 → [3,5,2,8,1,4] newIndex=3
↑ 交换 → [3,5,2,1,8,4] newIndex=4
↑ 交换 →[3,5,2,1,4,8]newIndex=5
第2轮 (n=5):次最大值
比较: [3,5,2,1,4,8]
↑ 保持 → [3,5,2,1,4,8]
↑ 交换 → [3,2,5,1,4,8] newIndex=2
↑ 交换 → [3,2,1,5,4,8] newIndex=3
↑ 交换 → [3,2,1,4,5,8] newIndex=4
第3轮 (n=4):次次最大值
比较: [3,2,1,4,5,8]
↑ 交换 → [2,3,1,4,5,8] newIndex=1
↑ 交换 → [2,1,3,4,5,8] newIndex=2
↑ 保持 → [2,1,3,4,5,8]
第4轮 (n=2):
比较: [2,1,3,4,5,8]
↑ 交换 → [1,2,3,4,5,8] newIndex=1
第5轮 (n=1):
无比较,newIndex=0,结束
最终结果: [1, 2, 3, 4, 5, 8]快速排序
随机化基准:可避免最坏情况,保证期望O(n log n)
快速排序使用分治策略 将一个数组分为两个子数组,然后递归地对子数组进行排序。
非稳定排序
双边循环法
- 挖坑法:使用双指针从两端向中间扫描,通过填坑方式交换元素,通过"填坑"的方式来移动元素,因此是直接覆盖(赋值)
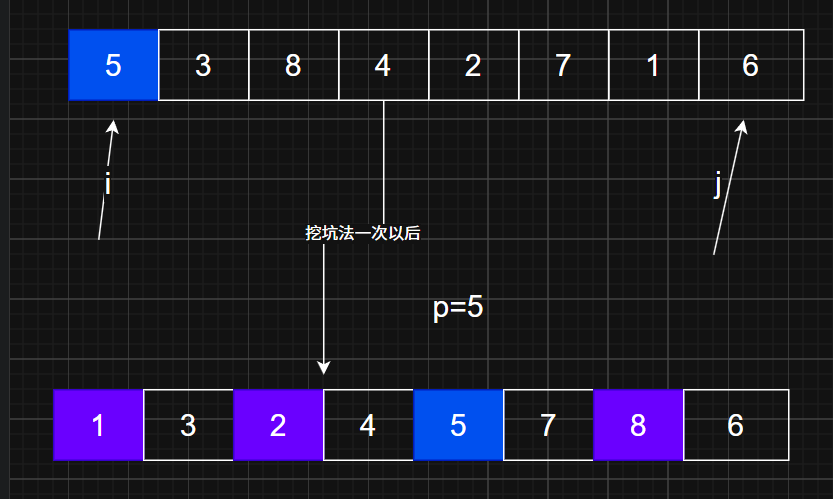
单边循环法
使用单指针从左到右扫描,通过mark标记边界,交换来将小于基准的元素移动到左侧。
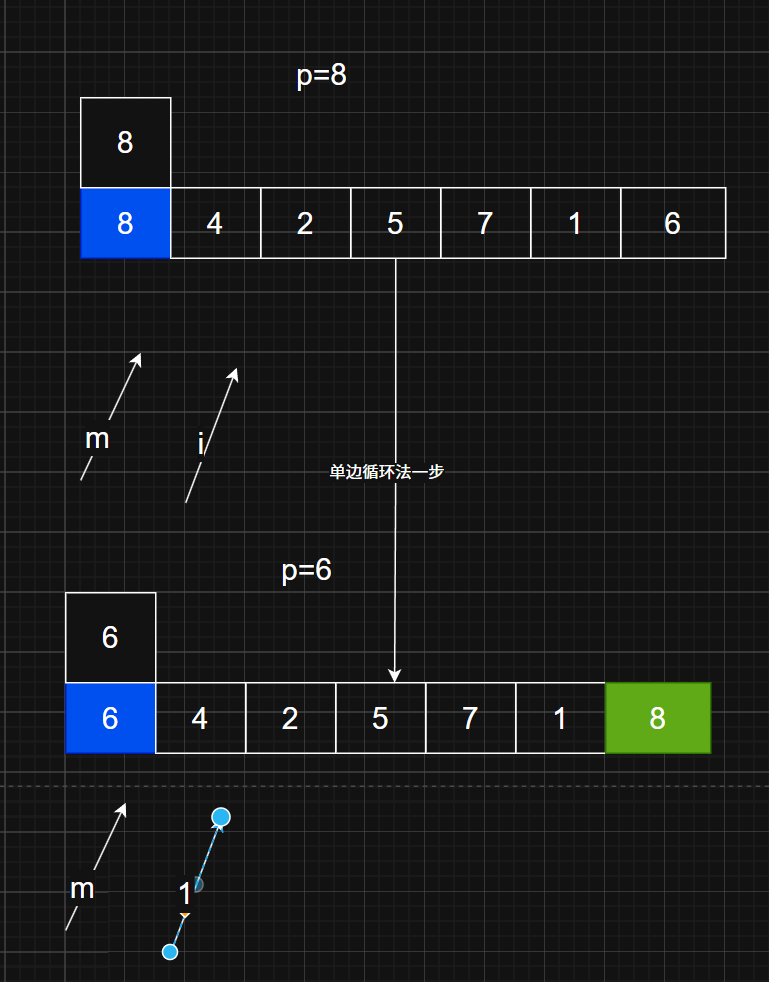
为什么一个用覆盖一个用交换?
- 挖坑法(双边循环法)之所以使用覆盖,是因为我们每次移动指针找到符合条件的元素时,直接将其赋值到另一个指针所指的"坑"里。这样,原来那个元素的位置就变成了新的"坑"。而基准元素在开始就被保存起来,最后再放回中间的位置。整个过程没有交换,只有赋值操作。
- 单边循环法(Lomuto)使用交换,是因为我们用一个mark指针来维护小于基准的区域的边界。当遇到一个小于基准的元素时,我们需要将其放到mark区域的末尾,而mark区域末尾的下一个元素是大于等于基准的,所以我们交换这两个元素。这样,小于基准的元素就被放到了左边,大于等于基准的元素被放到了右边。
代码
冒泡排序(bubbleSortV1)
使用双重循环,外层循环控制轮数,内层循环进行相邻元素的比较和交换。
每轮循环后,最大的元素会被移动到数组末尾,因此内层循环的范围随着轮数增加而减小。
基础版本,没有优化提前终止
c
#include <stdio.h>
int a[1000]; // 数据数组
int n; // 数组长度
// 交换函数
void swap(int *a, int *b) {
int temp = *a;
*a = *b;
*b = temp;
}
// 基础版冒泡排序
void bubbleSortV1() {
for (int i = 1; i < n; i++) { // 索引从1开始,需要进行n-1轮
for (int j = 1; j <= n - i; j++) { // 每轮比较次数递减
if (a[j] > a[j + 1]) {
swap(&a[j], &a[j + 1]);
}
}
}
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
}
bubbleSortV1();
for (int i = 1; i <= n; i++) {
printf("%d ", a[i]);
}
printf("\n");
return 0;
}如果没有发生交换,说明数组已经有序,可以提前结束排序。
isSorted = 0;
c
#include<stdio.h>
#include<stdlib.h>
int n,a[105];
//冒泡排序:就地排序 稳定的 O(n^2)
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
}
int t;
int flag=0;
for(int i=1;i<=n-1;i++)//枚举排序的趟数
{
flag=0;
//乱序区 1 ~~ n-i+1
for(int j=1;j<=n-i;j++)//枚举乱序区进行比较
{
if(a[j]>a[j+1])
{
flag=1;
t=a[j];
a[j]=a[j+1];
a[j+1]=t;
}
}
if(flag==0)break;
}
for(int i=1;i<=n;i++)
{
printf("%d ",a[i]);
}
printf("\n");
}循环多少轮,是由冒泡过程最后的交换的索引号为依据
引入变量记录最后一次交换的位置
newindex=0; // 第一轮为某个大于o的数 但是第二轮有序 newindex依旧大于o 跳不出去
c
#include <stdio.h>
int a[1000]; // 数据数组
int n; // 数组长度
// 交换函数
void swap(int *a, int *b) {
int temp = *a;
*a = *b;
*b = temp;
}
// 优化版冒泡排序
void bubbleSortOptimized() {
int newIndex;
int m = n; // 当前需要遍历的边界
//因为冒泡排序至少需要遍历一次数组,才能确定数组是否已经有序
do {
newIndex = 0; // 记录本轮最后一次交换的位置
for (int i = 1; i < m; i++) { // 索引从1开始
if (a[i] > a[i + 1]) {
swap(&a[i], &a[i + 1]);
newIndex = i; // 更新最后交换位置为当前索引
}
}
m = newIndex; // 更新下一轮的遍历边界
} while (newIndex > 0); // 只要本轮有交换就继续
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
}
bubbleSortOptimized();
for (int i = 1; i <= n; i++) {
printf("%d ", a[i]);
}
printf("\n");
return 0;
}快速排序(bubbleSortV1)
双边循环法
c
#include<stdio.h>
#include<stdlib.h>
int n,a[105];
//快速排序:空间复杂度O(logn) 不稳定 平均时间复杂度O(nlogn)----》最坏(当初始数据已经有序时)时间复杂度O(n^2)
void Qsort(int a[],int l,int r)
{
int p;
if(l<r)//待排序区间中至少有两个数据
{
int i=l,j=r,p=a[l];//选待排序区间第一个位置的数做基准数
while(i<j)
{
//先用j从后往前找比p小的数 放到i位置
while(i<j&&a[j]>p)j--;
if(i<j)
{
a[i]=a[j];
i++;
}
//先用i从前往后找比p大的数 放到j位置
while(i<j&&a[i]<p)i++;
if(i<j)
{
a[j]=a[i];
j--;
}
}
//i==j
a[i]=p;
Qsort(a,l,i-1);
Qsort(a,i+1,r);
}
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
}
Qsort(a,1,n);
for(int i=1;i<=n;i++)
{
printf("%d ",a[i]);
}
printf("\n");
}单边循环法
c
#include <stdio.h>
int a[1000], n;
void swap(int *a, int *b) {
int t = *a; *a = *b; *b = t;
}
int partition(int l, int r) {
int p = a[l], m = l;
//基准位置最后交换
for (int i = l + 1; i <= r; i++)
if (a[i] < p)
swap(&a[++m], &a[i]);
swap(&a[l], &a[m]);
return m;
}
void qsort2(int l, int r) {
if (l < r) {
int p = partition(l, r);
qsort2(l, p - 1);
qsort2(p + 1, r);
}
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
qsort2(1, n);
for (int i = 1; i <= n; i++) printf("%d ", a[i]);
printf("\n");
return 0;
}