leetcode hot100 226. 翻转二叉树 easy 递归 层序遍历 BFS

---

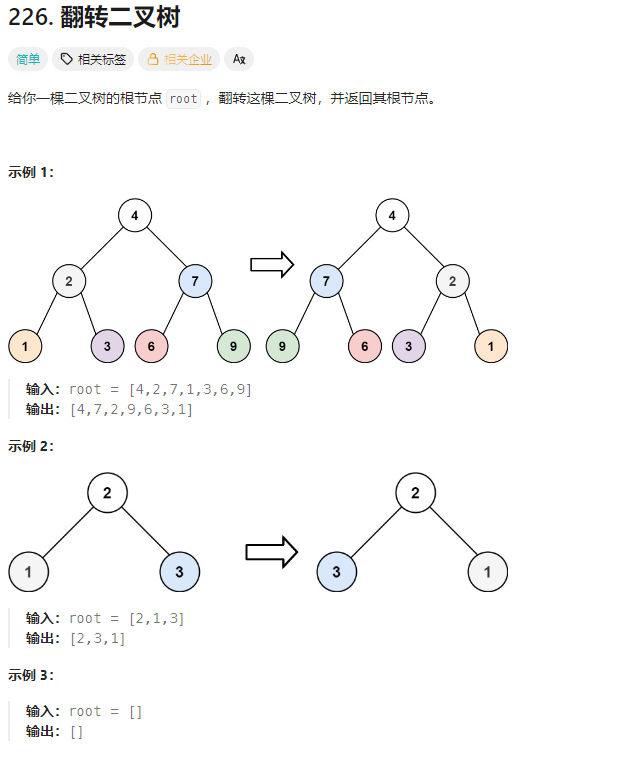
对于每一个节点，交换它的左孩子和右孩子

递归解法（自顶向下）

交换：把当前节点的左儿子和右儿子互换位置。

递归：对左儿子进行同样的翻转，对右儿子也进行同样的翻转。

1. 时间复杂度： O ( N ) O(N) O(N)：必须访问且仅访问树中的每一个节点一次。
2. 空间复杂度： O ( N ) O(N) O(N)：如果树退化成了一个链表（每个节点只有一个孩子），递归深度就是 N N N。此时复杂度为 O ( N ) O(N) O(N)。最好情况：如果是一棵完全平衡的二叉树，树的高度是 log ⁡ N \log N logN。此时复杂度为 O ( log ⁡ N ) O(\log N) O(logN)。

递归三部曲

1. 出口：作用：告诉程序什么时候停下来。（比如：节点为空、数值为 0）。
2. 操作：作用：在当前这一层你需要完成的任务。（例子：在翻转二叉树里是"交换左右孩子"；在中序遍历里是"把值填进列表"。）特点：只关注当前这一步，不操心以后。
3. 调用自己递归 ：作用：把剩下的任务交给"未来的自己"。特点：去处理左子树、右子树，或者 n − 1 n-1 n−1 的情况。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    # 原函数也是返回节点，递归直接用
    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:

        # 1. 递归出口
        if not root:
            return None

        # 2. 交换当前节点的左右子树
        root.left, root.right = root.right, root.left  # Python 特有的交换语法：a, b = b, a

        # 3. 递归地翻转子树
        self.invertTree(root.left)
        self.invertTree(root.right)

        # 4. 返回翻转后的根节点
        return root

1. 中序遍历：操作被"夹"在中间

在中序遍历里，操作是 res.append(node.val)。

为什么不先操作？ 把 append 放在最前面，它就变成前序遍历了。中序遍历的要求是"左-根-右"。所以必须先调用 inorderdfs(node.left)，

2. 最大深度：操作被"压"在最后

在最大深度里，操作是 max(left, right) + 1。

为什么不先操作？ 因为在算出左边多高、右边多高之前，没法操作。这属于后序位置的操作。只有拿到了子问题的答案，当前层的逻辑才能运行。

3. 翻转二叉树：操作在最前

翻转操作不需要知道子树的情况。只要看到这个节点

---

层序遍历 BFS

既然是"每一个节点都要交换左右孩子"，我们也可以像剥洋葱一样，一层一层地处理。

1. 时间复杂度： O ( N ) O(N) O(N)：必须访问且仅访问树中的每一个节点一次。
2. 空间复杂度： O ( N ) O(N) O(N)：元素最多的层

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

from collections import deque

class Solution:
    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:

        if not root:
            return None

        # 1. 初始化双端队列，先是顶层
        queue = deque([root])   # queue 操作"名单"

        #处理这一层的每个元素
        while queue:

            #2. 弹出队首节点（左）
            node = queue.popleft()

            # 3. 交换这个节点的左右孩子
            node.left, node.right = node.right, node.left   # 操作（交换）

            # 4.  把节点的左右子树加入队列
            if node.left:
                queue.append(node.left)
            if node.right:
                queue.append(node.right)

        
        return root