卷积(convolution)是深度学习中非常有用的计算操作,主要用于提取图像的特征。在近几年来深度学习快速发展的过程中,卷积从标准卷积演变出了反卷积、可分离卷积、分组卷积等各种类型,以适应于不同的场景。
本篇文章主要介绍一些基础的知识,更多的卷积类型可以参考:【图解AI:动图】各种类型的卷积,你认全了吗? - OSCHINA - 开源 × AI · 开发者生态社区
1 卷积层常见参数
卷积核(Kernel): 卷积操作的感受野,直观理解就是一个滤波矩阵,普遍使用的卷积核大小为3×3、5×5等;
步长(Stride): 卷积核遍历特征图时每步移动的像素,如步长为1则每次移动1个像素,步长为2则每次移动2个像素(即跳过1个像素),以此类推;
填充(Padding): 处理特征图边界的方式,一般有两种,一种是对边界外完全不填充,只对输入像素执行卷积操作,这样会使输出特征图的尺寸小于输入特征图尺寸;另一种是对边界外进行填充(一般填充为0),再执行卷积操作,这样可使输出特征图的尺寸与输入特征图的尺寸一致;【使用padding可以使得边界的特征被充分利用,让网络更公平地对待边界特征】
**通道(Channel):**卷积层的通道数(层数)。灰度图channel为1, RGB图channel为3.
如下图是一个卷积核(kernel)为3×3、步长(stride)为1、填充(padding)为1的二维卷积:
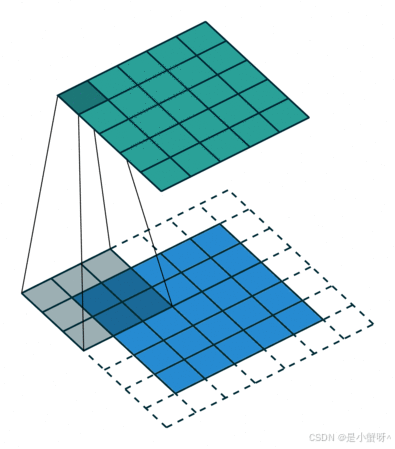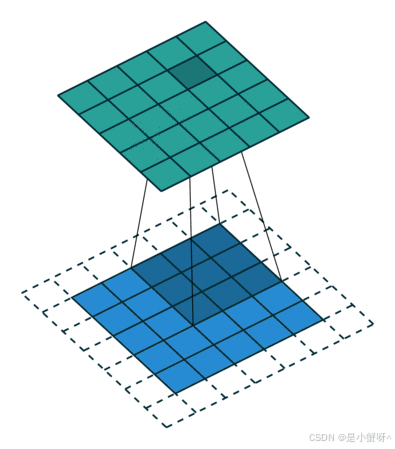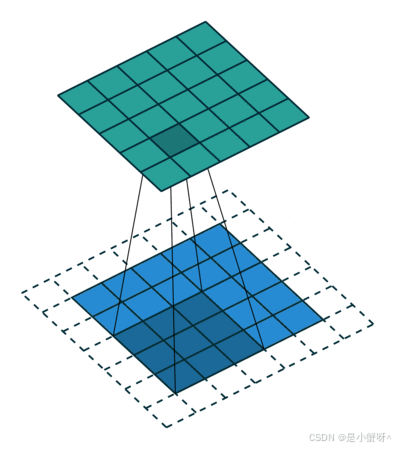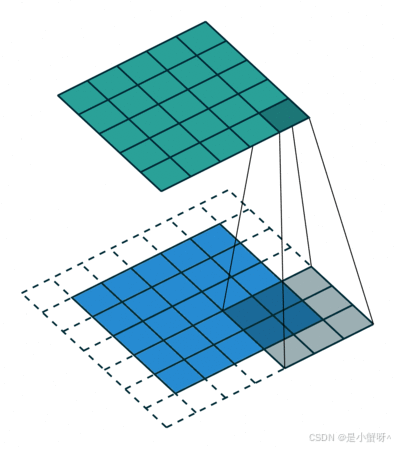
2 卷积的计算
卷积核在输入图像上扫描,将卷积核与输入图像中对应位置的数值逐个相乘,最后汇总求和,就得到该位置的卷积结果。不断移动卷积核,就可算出各个位置的卷积结果。如下图:
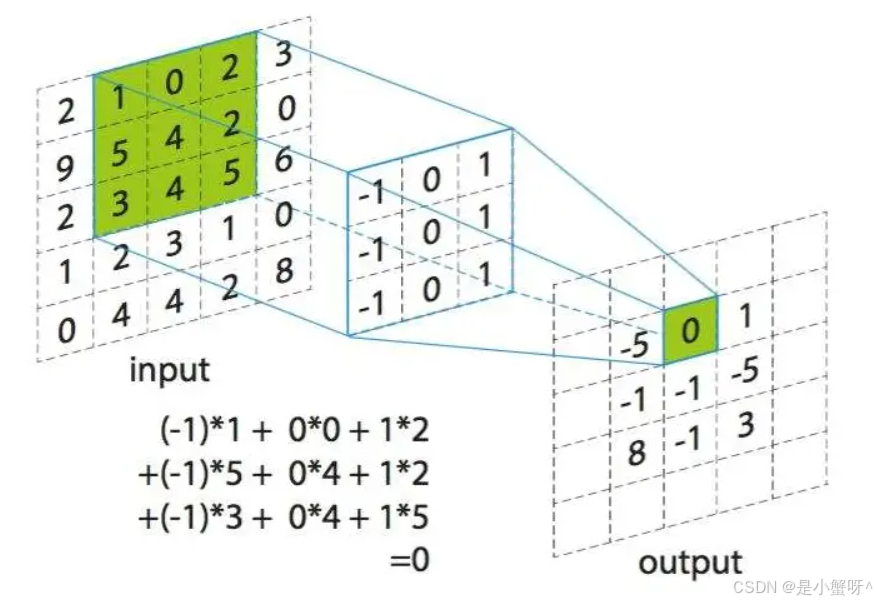
3 卷积的类型
(1)标准卷积
【1】二维卷积操作(单通道卷积)
只有一个通道(channel=1)的卷积。如下图是一个卷积核(kernel)为3×3、步长(stride)为1、填充(padding)为0的卷积:
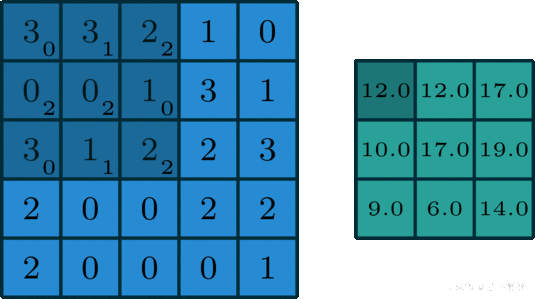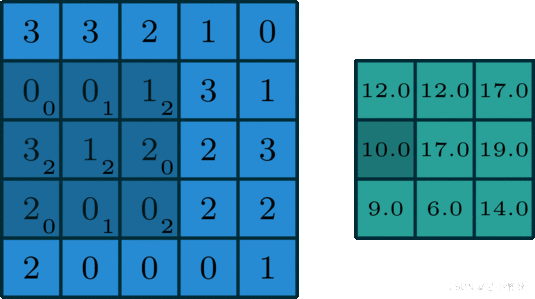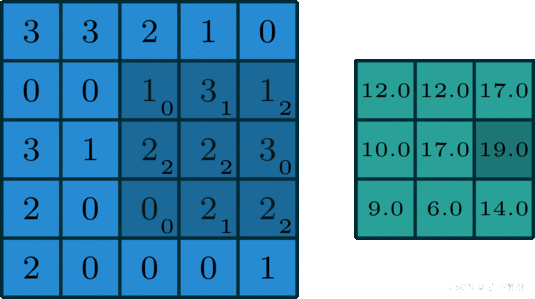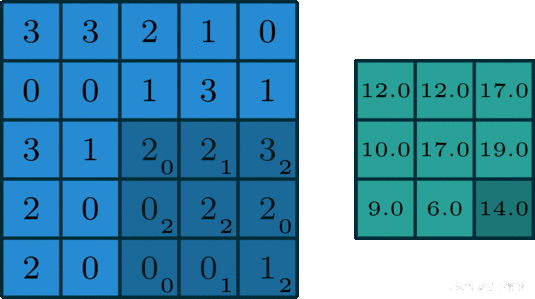
【2】二维卷积操作(多通道卷积)
拥有多个通道的卷积,例如处理彩色图像时,分别对R, G, B这3个层处理的3通道卷积,如下图:
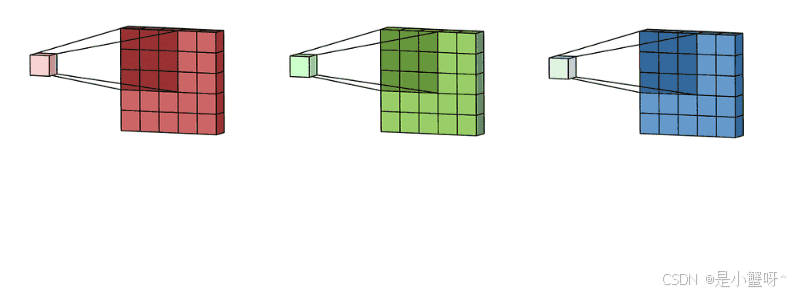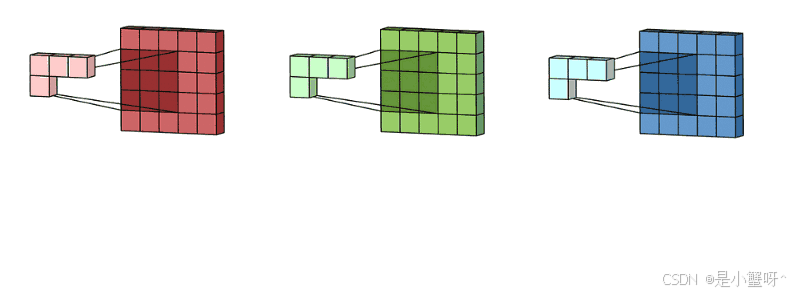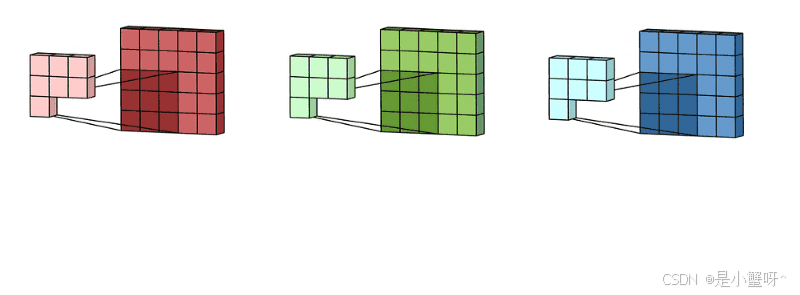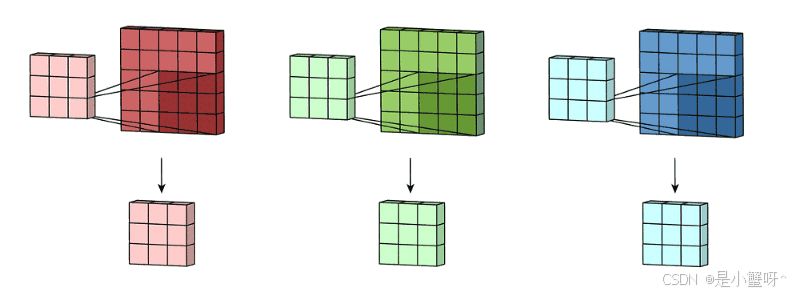
然后将这三个通道的卷积结果相加,得到最终的卷积结果,如下图:
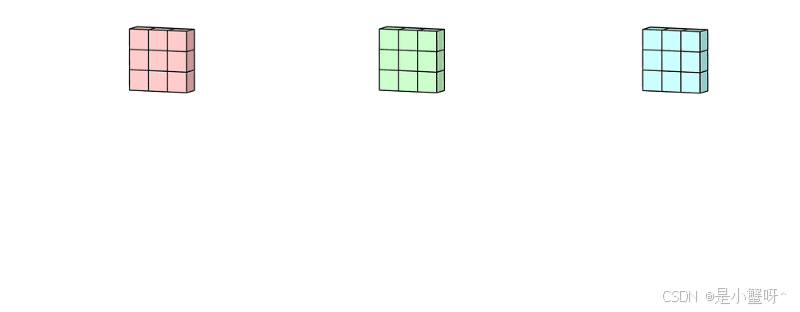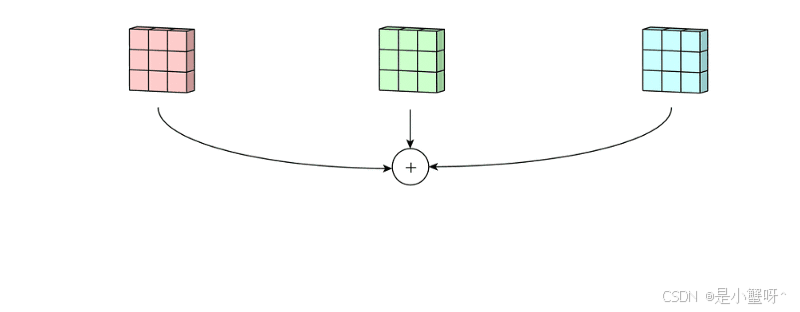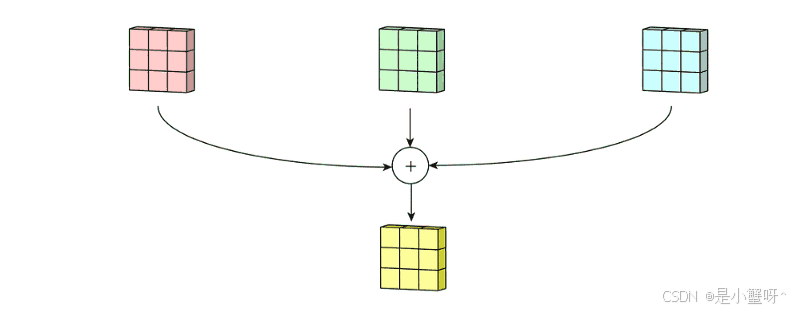
(2) 反卷积
卷积是对输入图像提取出特征(可能尺寸会变小),而所谓的"反卷积"便是进行相反的操作。但这里说是"反卷积"并不严谨,因为并不会完全还原到跟输入图像一样,一般是还原后的尺寸与输入图像一致,主要用于向上采样。从数学计算上看,"反卷积"相当于是将卷积核转换为稀疏矩阵后进行转置计算,因此,也被称为"转置卷积"
如下图,在2x2的输入图像上应用步长为1、边界全0填充的3x3卷积核,进行转置卷积(反卷积)计算,向上采样后输出的图像大小为4x4
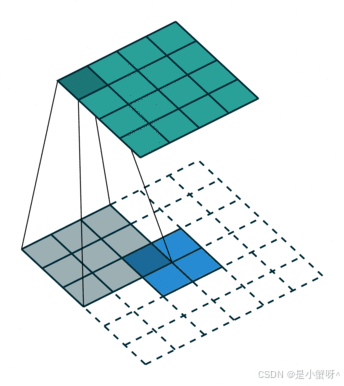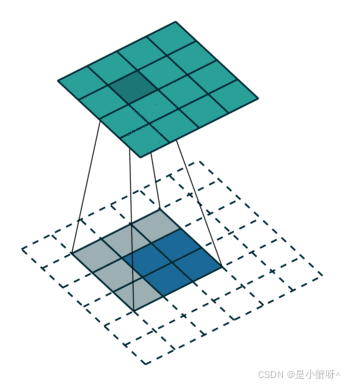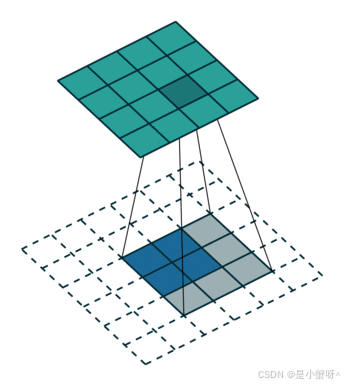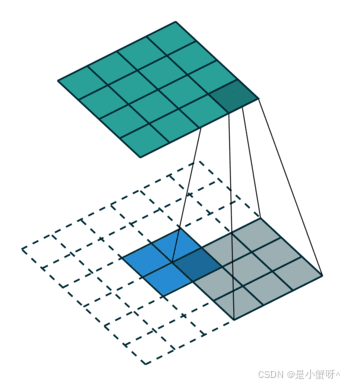
备注:对于处理普通的图片而言,使用二维卷积我觉得已经够用了,所以这边只记录这些,后面在项目中遇到别的卷积操作,会进行补充。
另外,感谢博主的知识共享,有想要了解更多的,可以参考:【图解AI:动图】各种类型的卷积,你认全了吗? - OSCHINA - 开源 × AI · 开发者生态社区
讲的很全面!