算法 数学归纳+反证的角度 推理总结的思路
lc2575
% 步步取模 实现整数拆分

class Solution {
public:
vector<int> divisibilityArray(string word, int m) {
vector<int> ans(word.length());
long long x = 0;
for (int i = 0; i < word.length(); i++) {
++x = (x * 10 + (word[i] - '0')) % m;++
ans[i] = x == 0;
}
return ans;
}
};
lc2577
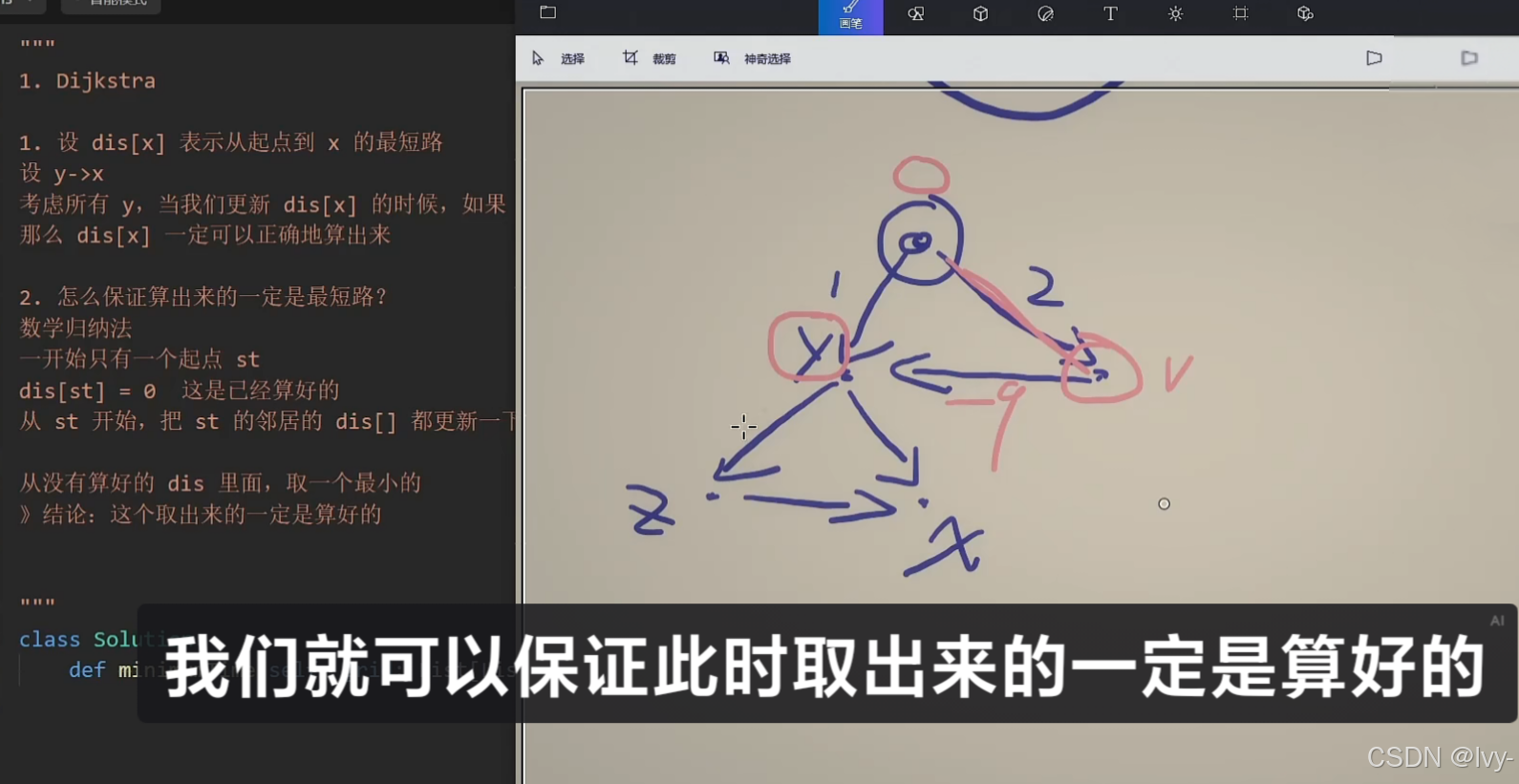
dijk 单源最短路 一开始只有一个起点 不可有负数
pq贪心更新 一步一步的取出 确定 选择
class Solution {
static constexpr int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
public:
int minimumTime(vector<vector<int>> &grid) {
int m = grid.size(), n = grid[0].size();
if (grid[0][1] > 1 && grid[1][0] > 1) // 无法「等待」
return -1;
int dis[m][n];
memset(dis, 0x3f, sizeof(dis));
dis[0][0] = 0;
priority_queue<tuple<int, int, int>, vector<tuple<int, int, int>>, greater<>> pq;
pq.emplace(0, 0, 0);
for (;;) { // 可以等待,就一定可以到达终点
auto[d, i, j] = pq.top();
pq.pop();
if (d > dis[i][j]) continue;
if (i == m - 1 && j == n - 1)
// 找到终点,此时 d 一定是最短路
return d;
for (auto &q : dirs) {
// 枚举周围四个格子
int x = i + q[0], y = j + q[1];
if (0 <= x && x < m && 0 <= y && y < n) {
int nd = max(d + 1, grid[x][y]);
nd += (nd - x - y) % 2;
// nd 必须和 x+y 同奇偶
++if (nd < dis[x][y]) {
dis[x][y] = nd;++ // 更新最短路
pq.emplace(nd, x, y);
}
}
}
}
}
};
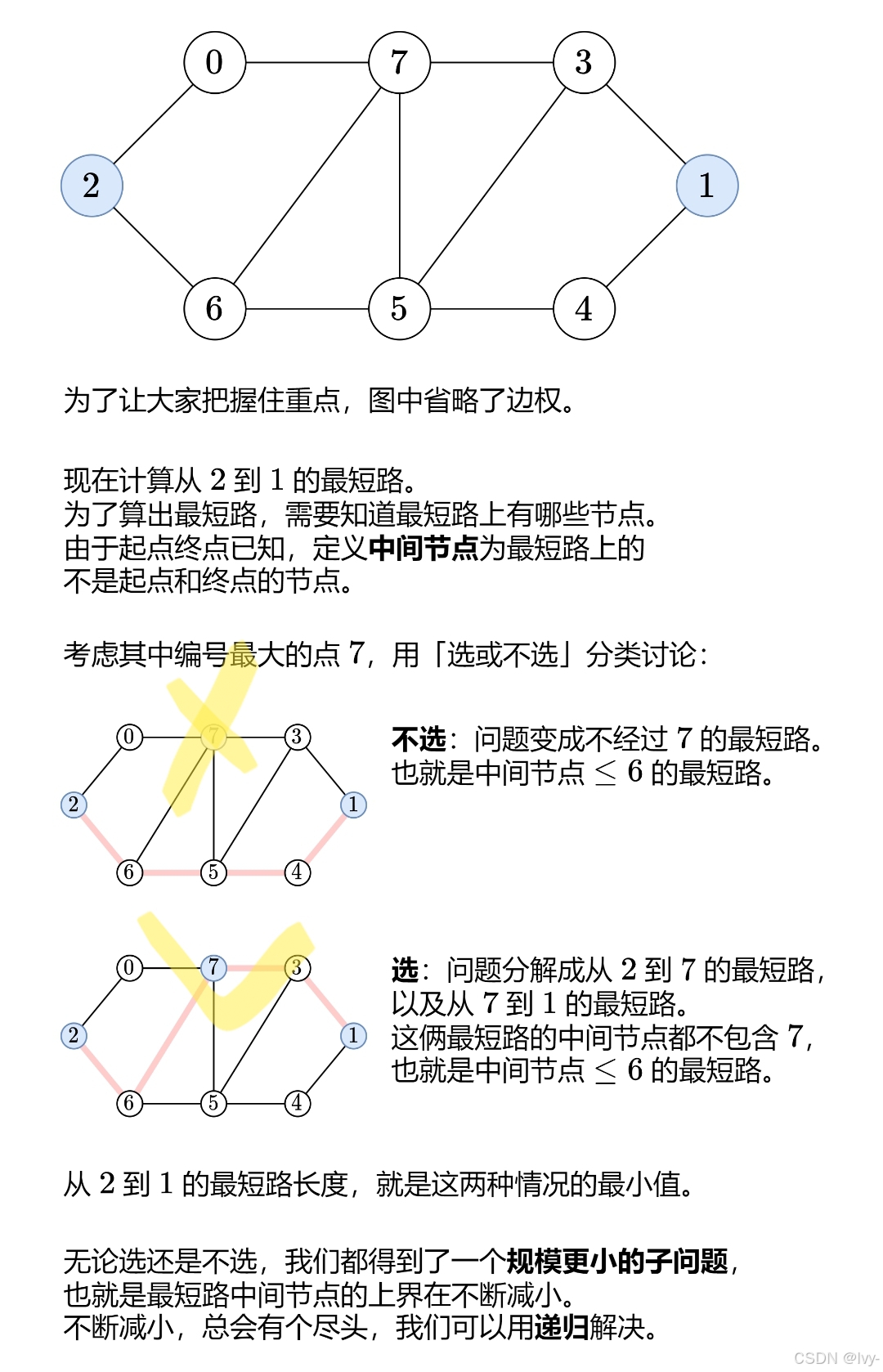
floyd 多源最短路
一种 选/不选 的dp思想
class Solution {
public:
int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
vector w(n, vector<int>(n, INT_MAX / 2)); // 防止加法溢出
for (auto& e: edges) {
int x = e[0], y = e[1], wt = e[2];
w[x][y] = w[y][x] = wt;
}
vector memo(n, vector(n, vector<int>(n)));
auto dfs = [&](this auto&& dfs, int k, int i, int j) -> int {
if (k < 0) { // 递归边界
return w[i][j];
}
auto& res = memo[k][i][j]; // 注意这里是引用
if (res) { // 之前计算过
return res;
}
return res = min(dfs(k - 1, i, j), dfs(k - 1, i, k) + dfs(k - 1, k, j));
};
int ans = 0;
int min_cnt = n;
for (int i = 0; i < n; i++) {
int cnt = 0;
for (int j = 0; j < n; j++) {
if (j != i && dfs(n - 1, i, j) <= distanceThreshold) {
cnt++;
}
}
if (cnt <= min_cnt) { // 相等时取最大的 i
min_cnt = cnt;
ans = i;
}
}
return ans;
}
};
lc2977
tire+floyd+dp
题解
struct Node {
Node* son[26]{};
int sid = -1; // 字符串的编号
};
class Solution {
public:
long long minimumCost(string source, string target, vector<string>& original, vector<string>& changed, vector<int>& cost) {
Node* root = new Node();
int sid = 0;
auto put = [&](string& s) -> int {
Node* o = root;
for (char b: s) {
int i = b - 'a';
if (o->son[i] == nullptr) {
o->son[i] = new Node();
}
o = o->son[i];
}
if (o->sid < 0) {
o->sid = sid++;
}
return o->sid;
};
// 初始化距离矩阵
int m = cost.size();
vector dis(m * 2, vector<int>(m * 2, INT_MAX / 2));
for (int i = 0; i < m * 2; i++) {
dis[i][i] = 0;
}
for (int i = 0; i < m; i++) {
int x = put(original[i]);
int y = put(changed[i]);
dis[x][y] = min(dis[x][y], cost[i]);
}
// Floyd 求任意两点最短路
for (int k = 0; k < sid; k++) {
for (int i = 0; i < sid; i++) {
if (dis[i][k] == INT_MAX / 2) { // 加上这句话,巨大优化!
continue;
}
for (int j = 0; j < sid; j++) {
dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
}
}
}
int n = source.size();
vector<long long> f(n + 1);
for (int i = n - 1; i >= 0; i--) {
// 不修改 source[i]
f[i] = source[i] == target[i] ? f[i + 1] : LONG_LONG_MAX / 2;
Node* p = root;
Node* q = root;
for (int j = i; j < n; j++) {
p = p->son[source[j] - 'a'];
q = q->son[target[j] - 'a'];
if (p == nullptr || q == nullptr) {
break;
}
if (p->sid < 0 || q->sid < 0) {
continue;
}
// 修改从 i 到 j 的这一段
int d = dis[p->sid][q->sid];
if (d < INT_MAX / 2) {
f[i] = min(f[i], dis[p->sid][q->sid] + f[j + 1]);
}
}
}
return f[0] < LONG_LONG_MAX / 2 ? f[0] : -1;
}
};