我爱学算法之—— 递归回溯综合（二）

一、字母大小写全排列

题目解析

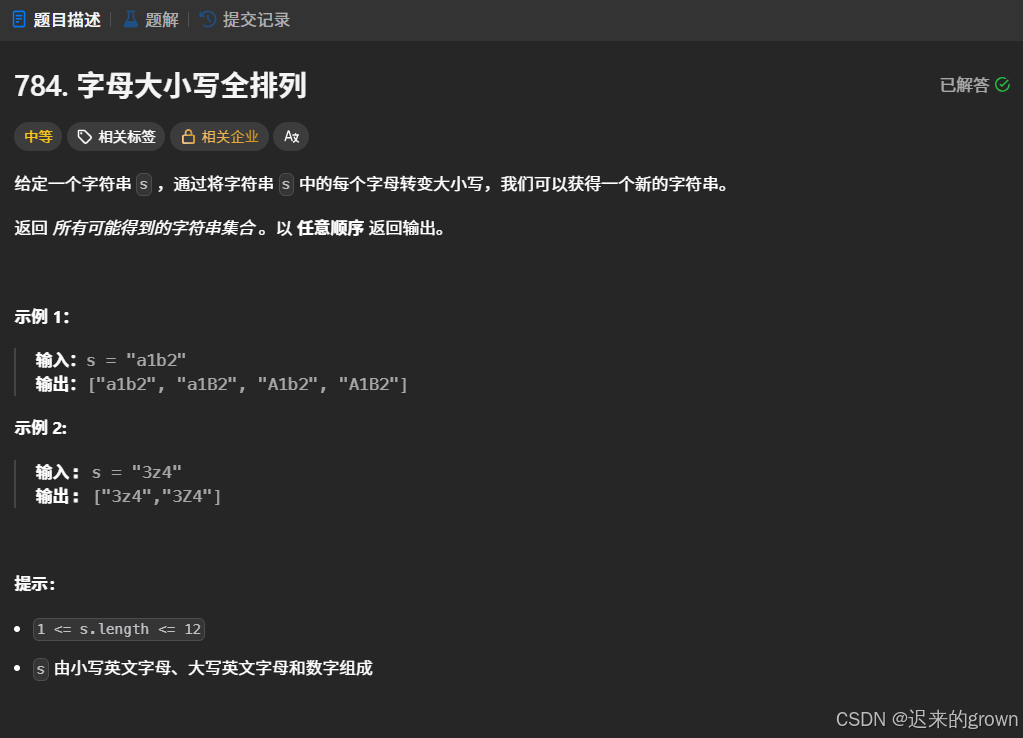
给定一个字符s，由小写英文字母、大写英文字母和数字组成；这里通过修改s中的每一个字母转变大小写，获得应该新的字符串。

最终返回所有可能得到的字符串集合。

算法思路

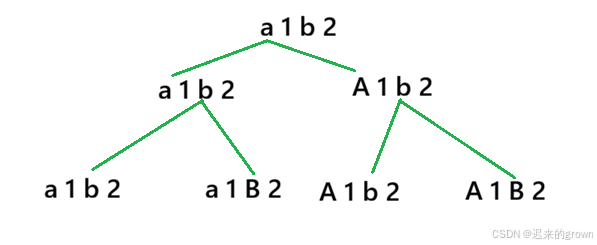
这里对于字符串s中的任意一个字母，无论它是大写还是小写，修改之后就两种情况：大写 、小写

和以往的递归回溯题目不同的是：字符串s中，不一定每一个字符都是字母，这里只能对字母进行大小写转换。

在递归时，就需要进行遍历寻找下一个字母，然后进行分支递归。

代码实现

class Solution {
    vector<string> ret;

public:
    void dfs(string& s, int pos) {
        if (pos == s.size()) {
            cout << s << endl;
            ret.push_back(s);
            return;
        }
        int i = pos;
        while (i < s.size() && s[i] >= '0' && s[i] <= '9')
            i++;
        if (i == s.size()) {
            ret.push_back(s);
            cout << s << endl;
            return;
        }
        char ch = s[i]; // 记录初始字母
        // 变小写
        if (ch >= 'A' && ch <= 'Z')
            s[i] += 32;
        dfs(s, i + 1);
        // 回溯
        s[i] = ch;
        // 变大写
        if (ch >= 'a' && ch <= 'z')
            s[i] -= 32;
        dfs(s, i + 1);
        // 回溯
        s[i] = ch;
    }
    vector<string> letterCasePermutation(string s) {
        dfs(s, 0);
        return ret;
    }
};

二、优美的排列

题目解析

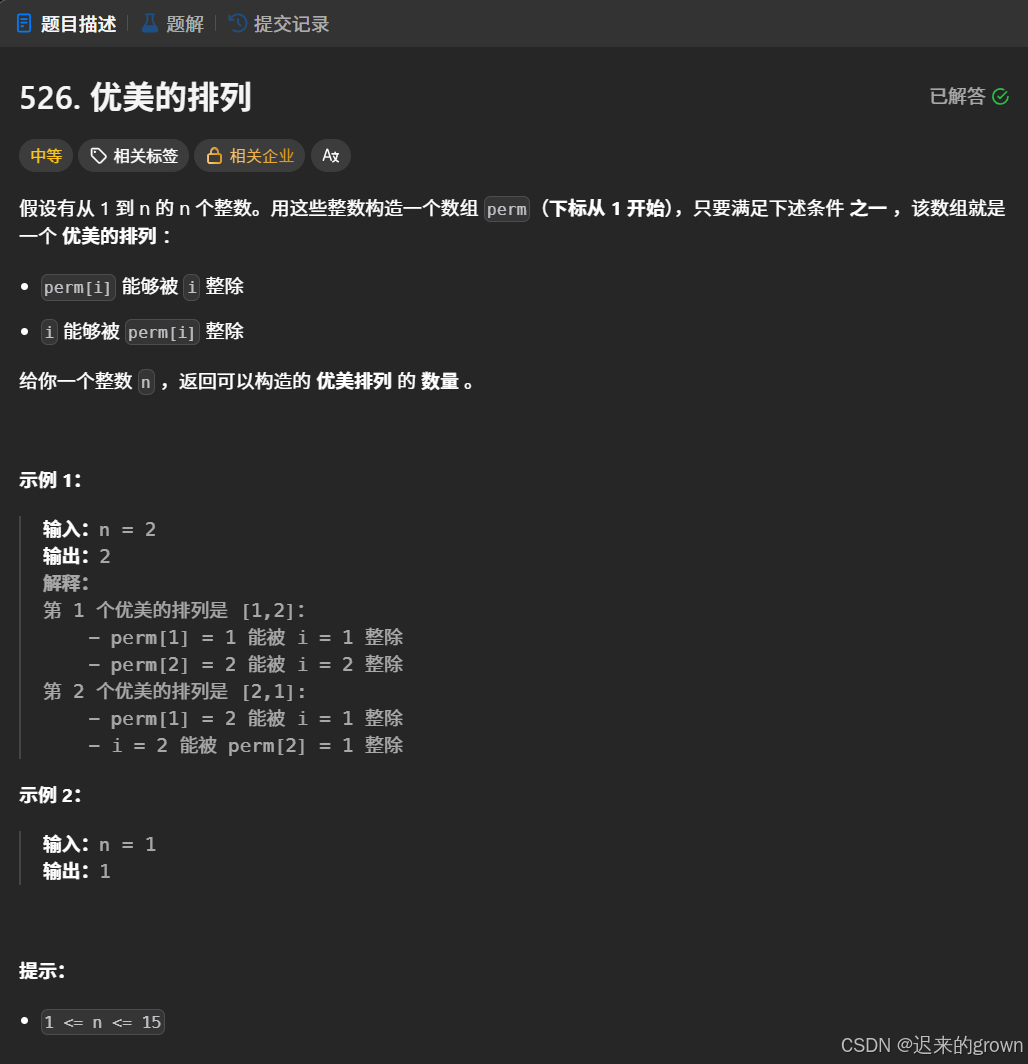
给定一个数n，用1 - n的n个整数构造一个数组perm(下标从1开始)

数组perm满足（其中一个）：

• perm[i]能被i整除
• i能被perm[i]整除

最终返回能构成perm数组的个数。

算法思路

对于这道题，整体思路还是非常简单的：

从第1个位置开始，判断1-n中每一个数是否能够放到该位置，然后递归选择下一个位置的数；

最终选择完最后一个位置的数即为找到一个满足条件的perm数组，统计个数即可。

代码实现

class Solution {
    int ret = 0;
    bool vis[20] = {false};

public:
    void dfs(int n, int pos) {
        if (pos > n) {
            ++ret;
            return;
        }
        for (int i = 1; i <= n; i++) {
            if (!vis[i] && (i % pos == 0 || pos % i == 0)) {
                vis[i] = true;
                dfs(n, pos + 1);
                vis[i] = false;
            }
        }
    }
    int countArrangement(int n) {
        dfs(n, 1);
        return ret;
    }
};

三、N 皇后

题目解析

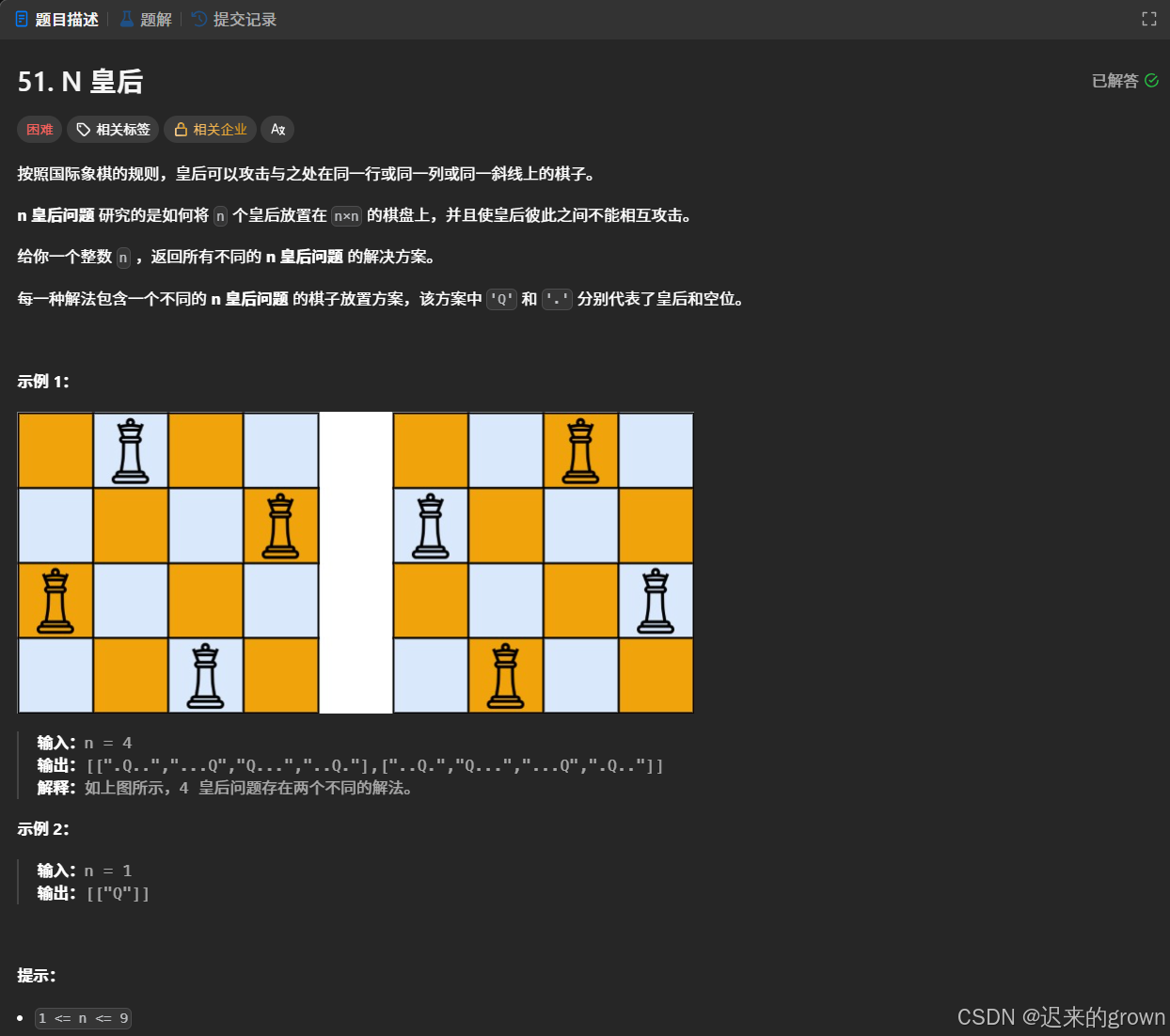
经典的 N皇后 问题：

n*n的棋盘中，要放置n个皇后，其中在同一行或者同一列或者同一斜线上

算法思路

同一行中，只存在一个Q（皇后）：通过递归，在某一行选择一个位置放置皇后。

同一列、同一斜线上只存在一个Q皇后：

在递归到第i行，选择一个位置放置Q之前，判断该位置是否可以放置（判断当前列、左上斜线、右上斜线部分是否存在 Q即可）

因为这里递归从第0行开始放置Q，当递归到第i行时，判断某个位置是否可以放置，只需要判断第0行到第i-1行对应列/斜线上是否存在Q即可

优化：

每次的循环判断对应列、对角线是否存在皇后，这也太麻烦了；

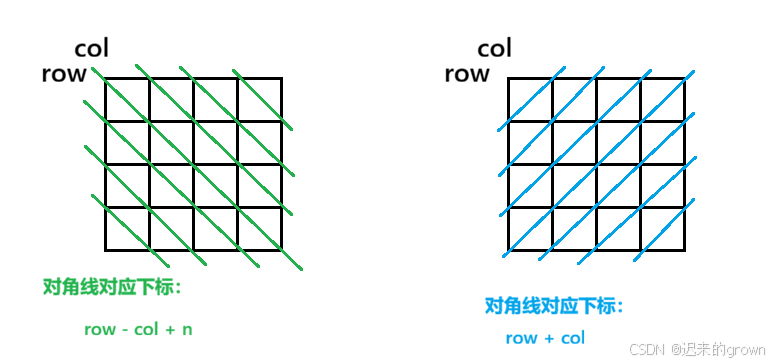
这里就可以定义数组col、dig1、dig2分别记录每一列、每一个对角线是否存在Q；这样就无需去循环判断当前位置是否满足条件了，直接判断对应列、对应对角线是否存在Q即可；

递归 ：在某一行中选择一个位置放置Q

剪枝 ：如果当前列、对角线上已经存在了Q；即当前位置不能放置，进行剪枝。

回溯 ：当前位置能够放置Q，并且递归（在后续行中选择完毕）结束；进行回溯。

对角线与数组下标的对应关系：

代码实现

class Solution {
    vector<vector<string>> ret;
    vector<string> path;
public:
    bool isOk(int n, int x, int y) {
        for (int i = 0; i < x; i++)
            if (path[i][y] == 'Q')
                return false;
        for (int i = x - 1, j = y - 1; i >= 0 && j >= 0; i--, j--)
            if (path[i][j] == 'Q')
                return false;
        for (int i = x - 1, j = y + 1; i >= 0 && j < n; i--, j++)
            if (path[i][j] == 'Q')
                return false;
        return true;
    }
    void dfs(int n, int line) {
        if (line == n) {
            ret.push_back(path);
            return;
        }
        for (int i = 0; i < n; i++) {
            // 从pos行选择一个位置
            if (isOk(n, line, i)) {
                path[line][i] = 'Q';
                dfs(n, line + 1);
                path[line][i] = '.';
            }
        }
    }
    vector<vector<string>> solveNQueens(int n) {
        path.resize(n, string(n, '.'));
        dfs(n, 0);
        return ret;
    }
};

优化：

class Solution {
    vector<vector<string>> ret;
    vector<string> path;
    bool col[10], dig1[20], dig2[20];
public:
    void dfs(int n, int line) {
        if (line == n) {
            ret.push_back(path);
            return;
        }
        for (int i = 0; i < n; i++) {
            // 从pos行选择一个位置
            if (!col[i] && !dig1[line - i + n] && !dig2[line + i]) {
                path[line][i] = 'Q';
                col[i] = dig1[line - i + n] = dig2[line + i] = true;
                dfs(n, line + 1);
                path[line][i] = '.';
                col[i] = dig1[line - i + n] = dig2[line + i] = false;
            }
        }
    }
    vector<vector<string>> solveNQueens(int n) {
        path.resize(n, string(n, '.'));
        dfs(n, 0);
        return ret;
    }
};

四、单词搜索

题目解析

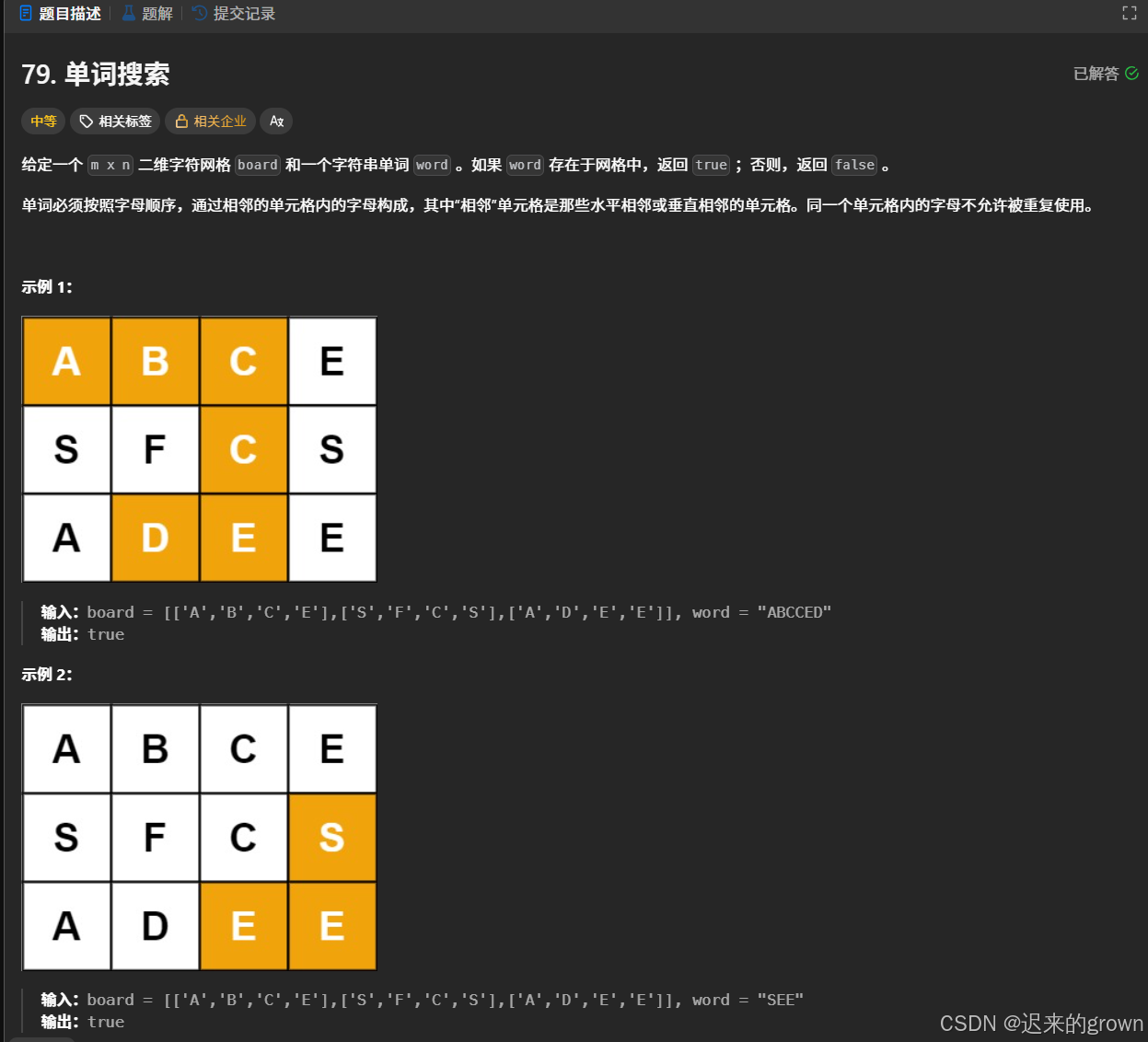
给定一个m*n的二维数组board和一个字符串单词word，判断单词word是否在board数组中。

算法思路

整体思路：

遍历board二维数组，找到word单词第一个字母的位置，进行一次深度优先遍历；如果存在word单词就返回true。

代码实现

class Solution {
    int dx[4] = {0, 0, 1, -1};
    int dy[4] = {1, -1, 0, 0};
    bool vis[20][20];
public:
    bool dfs(vector<vector<char>>& board, string& word, int i, int j, int pos) {
        if (pos == word.size())
            return true;
        int m = board.size();
        int n = board[0].size();
        for (int k = 0; k < 4; k++) {
            int x = i + dx[k];
            int y = j + dy[k];
            if (x >= 0 && y >= 0 && x < m && y < n && !vis[x][y] &&
                board[x][y] == word[pos]) {
                vis[x][y] = true;
                if (dfs(board, word, x, y, pos + 1))
                    return true;
                vis[x][y] = false;
            }
        }
        return false;
    }
    bool exist(vector<vector<char>>& board, string word) {
        int m = board.size();
        int n = board[0].size();
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (board[i][j] == word[0]) {
                    vis[i][j] = true;
                    if (dfs(board, word, i, j, 1))
                        return true;
                    vis[i][j] = false;
                }
            }
        }
        return false;
    }
};

本篇文章到这里就结束了，感谢支持

我的博客即将同步至腾讯云开发者社区，邀请大家一同入驻：https://cloud.tencent.com/developer/support-plan?invite_code=2oul0hvapjsws