【机器学习教程】第04章指数族分布

第04章指数族分布

前言

在概率论的浩瀚海洋中,指数族分布 (Exponential Family) 是一座灯塔。它不仅仅是高斯分布、伯努利分布等常见分布的集合,更是它们背后的通用模版。

为什么线性回归、逻辑回归的梯度公式长得一模一样?为什么最大熵原理最终指向了它?为什么贝叶斯推断需要共轭先验?

本章将带你深入这个"上帝的指纹",揭示看似无关的算法背后统一的数学本质。学完本章,你将不再是一个个地记忆公式,而是掌握了生成公式的元规则。

引言
[1. 指数族分布的定义](#1. 指数族分布的定义)
- [1.1 从伯努利分布开始](#1.1 从伯努利分布开始)
- [1.2 高斯分布的改写](#1.2 高斯分布的改写)
- [1.3 指数族的标准形式](#1.3 指数族的标准形式)
- [1.4 对数配分函数的定义](#1.4 对数配分函数的定义)
- [1.5 常见分布的指数族形式](#1.5 常见分布的指数族形式)
[2. 指数族分布的性质](#2. 指数族分布的性质)
- [2.1 一阶导数:期望](#2.1 一阶导数:期望)
- [2.2 二阶导数:方差](#2.2 二阶导数:方差)
- [2.3 Fisher 信息矩阵](#2.3 Fisher 信息矩阵)
- [2.4 最大似然估计的矩匹配](#2.4 最大似然估计的矩匹配)
[3. 指数族分布与最大熵](#3. 指数族分布与最大熵)
- [3.1 问题:如何选择概率分布?](#3.1 问题:如何选择概率分布?)
- [3.2 熵与最大熵原理](#3.2 熵与最大熵原理)
- [3.3 推导:最大熵分布是指数族](#3.3 推导:最大熵分布是指数族)
- [3.4 例子 1:高斯分布](#3.4 例子 1:高斯分布)
- [3.5 例子 2:指数分布](#3.5 例子 2:指数分布)
- [3.6 例子 3:离散均匀分布](#3.6 例子 3:离散均匀分布)
[4. 指数族分布与广义线性模型 (GLM)](#4. 指数族分布与广义线性模型 (GLM))
- [4.1 问题:线性回归与逻辑回归的统一](#4.1 问题:线性回归与逻辑回归的统一)
- [4.2 GLM 的定义](#4.2 GLM 的定义)
- [4.3 核心推导:GLM 的统一梯度公式](#4.3 核心推导:GLM 的统一梯度公式)
- [4.4 Hessian 矩阵:凸性保证](#4.4 Hessian 矩阵:凸性保证)
- [4.5 例子 1:线性回归 (高斯 GLM)](#4.5 例子 1:线性回归 (高斯 GLM))
- [4.6 例子 2:逻辑回归 (伯努利 GLM)](#4.6 例子 2:逻辑回归 (伯努利 GLM))
- [4.7 例子 3:泊松回归 (泊松 GLM)](#4.7 例子 3:泊松回归 (泊松 GLM))
- [4.8 GLM 的几何理解](#4.8 GLM 的几何理解)
[5. 总结](#5. 总结)
- [5.1 主要结论](#5.1 主要结论)
- [5.2 为什么指数族如此重要?](#5.2 为什么指数族如此重要?)
- [5.3 关键公式速查表](#5.3 关键公式速查表)
参考文献

引言

在机器学习中,我们会遇到各种各样的概率分布:

线性回归使用高斯分布 N ( μ , σ 2 ) \mathcal{N}(\mu, \sigma^2) N(μ,σ2)
逻辑回归使用伯努利分布 Bernoulli ( μ ) \text{Bernoulli}(\mu) Bernoulli(μ)
泊松回归使用泊松分布 Poisson ( λ ) \text{Poisson}(\lambda) Poisson(λ)

它们看起来截然不同:高斯处理连续变量,伯努利处理二元事件,泊松处理计数。但它们实际上共享同一个数学结构 ------这就是指数族分布。

本章我们将:

从具体分布推导出指数族的统一形式
深入理解对数配分函数的核心性质
从信息论角度理解指数族的必然性(最大熵原理)
揭示广义线性模型的统一本质

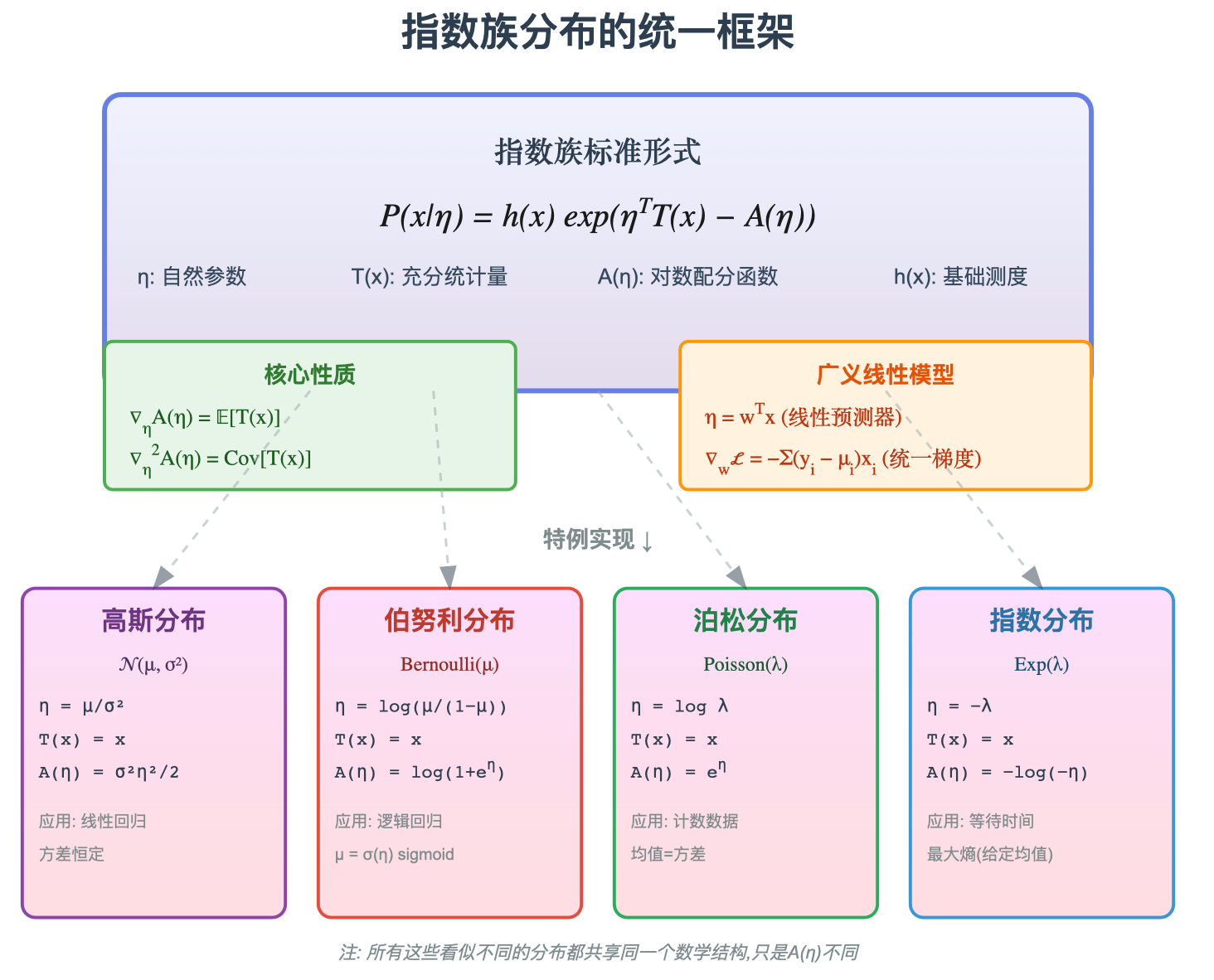
图1: 指数族分布的统一视角------看似截然不同的分布,实际上都是同一个模版 P ( x ∣ η ) = h ( x ) exp ⁡ ( η T T ( x ) − A ( η ) ) P(x|\eta) = h(x)\exp(\eta^T T(x) - A(\eta)) P(x∣η)=h(x)exp(ηTT(x)−A(η)) 的特例,唯一的差异在于对数配分函数 A ( η ) A(\eta) A(η) 的形式。

1. 指数族分布的定义

1.1 从伯努利分布开始

考虑抛硬币实验, x ∈ { 0 , 1 } x \in \{0, 1\} x∈{0,1},正面概率为 μ \mu μ:

P ( x ∣ μ ) = μ x ( 1 − μ ) 1 − x P(x|\mu) = \mu^x (1-\mu)^{1-x} P(x∣μ)=μx(1−μ)1−x

取对数:

log ⁡ P ( x ∣ μ ) = x log ⁡ μ + ( 1 − x ) log ⁡ ( 1 − μ ) \log P(x|\mu) = x \log \mu + (1-x) \log(1-\mu) logP(x∣μ)=xlogμ+(1−x)log(1−μ)

重新整理:

log ⁡ P ( x ∣ μ ) = x log ⁡ μ + log ⁡ ( 1 − μ ) − x log ⁡ ( 1 − μ ) = x [ log ⁡ μ − log ⁡ ( 1 − μ ) ] + log ⁡ ( 1 − μ ) = x log ⁡ μ 1 − μ + log ⁡ ( 1 − μ ) \begin{aligned} \log P(x|\mu) &= x \log \mu + \log(1-\mu) - x \log(1-\mu) \\ &= x \left[\log \mu - \log(1-\mu)\right] + \log(1-\mu) \\ &= x \log \frac{\mu}{1-\mu} + \log(1-\mu) \end{aligned} logP(x∣μ)=xlogμ+log(1−μ)−xlog(1−μ)=x[logμ−log(1−μ)]+log(1−μ)=xlog1−μμ+log(1−μ)

引入新参数 η = log ⁡ μ 1 − μ \eta = \log \frac{\mu}{1-\mu} η=log1−μμ (logit 函数)。注意到 1 − μ = 1 1 + e η 1-\mu = \frac{1}{1+e^\eta} 1−μ=1+eη1,因此:

log ⁡ ( 1 − μ ) = − log ⁡ ( 1 + e η ) \log(1-\mu) = -\log(1+e^\eta) log(1−μ)=−log(1+eη)

代入得:

log ⁡ P ( x ∣ η ) = x η − log ⁡ ( 1 + e η ) \log P(x|\eta) = x \eta - \log(1+e^\eta) logP(x∣η)=xη−log(1+eη)

指数化:

P ( x ∣ η ) = exp ⁡ ( η x − log ⁡ ( 1 + e η ) ) P(x|\eta) = \exp\left(\eta x - \log(1+e^\eta)\right) P(x∣η)=exp(ηx−log(1+eη))

观察这个形式:

参数 η \eta η 乘以数据 x x x
减去一个只依赖于 η \eta η 的项 log ⁡ ( 1 + e η ) \log(1+e^\eta) log(1+eη)

1.2 高斯分布的改写

考虑高斯分布 N ( μ , σ 2 ) \mathcal{N}(\mu, \sigma^2) N(μ,σ2) (假设 σ 2 \sigma^2 σ2 已知):

P ( x ∣ μ ) = 1 2 π σ 2 exp ⁡ ( − ( x − μ ) 2 2 σ 2 ) P(x|\mu) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right) P(x∣μ)=2πσ2 1exp(−2σ2(x−μ)2)

展开平方项:

− ( x − μ ) 2 2 σ 2 = − x 2 2 σ 2 + μ x σ 2 − μ 2 2 σ 2 -\frac{(x-\mu)^2}{2\sigma^2} = -\frac{x^2}{2\sigma^2} + \frac{\mu x}{\sigma^2} - \frac{\mu^2}{2\sigma^2} −2σ2(x−μ)2=−2σ2x2+σ2μx−2σ2μ2

因此:

P ( x ∣ μ ) = 1 2 π σ 2 exp ⁡ ( − x 2 2 σ 2 ) ⏟ h ( x ) exp ⁡ ( μ σ 2 x − μ 2 2 σ 2 ) P(x|\mu) = \underbrace{\frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{x^2}{2\sigma^2}\right)}_{h(x)} \exp\left(\frac{\mu}{\sigma^2} x - \frac{\mu^2}{2\sigma^2}\right) P(x∣μ)=h(x) 2πσ2 1exp(−2σ2x2)exp(σ2μx−2σ2μ2)

定义自然参数 η = μ σ 2 \eta = \frac{\mu}{\sigma^2} η=σ2μ,则 μ 2 2 σ 2 = σ 2 η 2 2 \frac{\mu^2}{2\sigma^2} = \frac{\sigma^2 \eta^2}{2} 2σ2μ2=2σ2η2:

P ( x ∣ η ) = h ( x ) exp ⁡ ( η x − σ 2 η 2 2 ) P(x|\eta) = h(x) \exp\left(\eta x - \frac{\sigma^2 \eta^2}{2}\right) P(x∣η)=h(x)exp(ηx−2σ2η2)

再次观察:同样的模式!

参数 η \eta η 乘以数据 x x x
减去一个只依赖于 η \eta η 的项
外加一个与参数无关的基础项 h ( x ) h(x) h(x)

1.3 指数族的标准形式

基于以上观察,我们定义指数族分布:

P ( x ∣ η ) = h ( x ) exp ⁡ ( η T T ( x ) − A ( η ) ) \boxed{P(x|\eta) = h(x) \exp\left(\eta^T T(x) - A(\eta)\right)} P(x∣η)=h(x)exp(ηTT(x)−A(η))

其中:

η ∈ R d \eta \in \mathbb{R}^d η∈Rd: 自然参数 (Natural Parameter)
T ( x ) ∈ R d T(x) \in \mathbb{R}^d T(x)∈Rd : 充分统计量 (Sufficient Statistic),是关于数据 x x x 的函数
A ( η ) ∈ R A(\eta) \in \mathbb{R} A(η)∈R: 对数配分函数 (Log-Partition Function)
h ( x ) > 0 h(x) > 0 h(x)>0 : 基础测度 (Base Measure),与参数 η \eta η 无关

充分统计量的含义 : T ( x ) T(x) T(x) 包含了关于参数 η \eta η 的所有信息。对于 i.i.d. 样本 { x 1 , ... , x N } \{x_1, \ldots, x_N\} {x1,...,xN},充分统计量为 ∑ i = 1 N T ( x i ) \sum_{i=1}^N T(x_i) ∑i=1NT(xi) 或其均值 T ˉ = 1 N ∑ i = 1 N T ( x i ) \bar{T} = \frac{1}{N}\sum_{i=1}^N T(x_i) Tˉ=N1∑i=1NT(xi)。

1.4 对数配分函数的定义

概率分布必须归一化:

∫ P ( x ∣ η ) d x = ∫ h ( x ) exp ⁡ ( η T T ( x ) − A ( η ) ) d x = 1 \int P(x|\eta) \, dx = \int h(x) \exp(\eta^T T(x) - A(\eta)) \, dx = 1 ∫P(x∣η)dx=∫h(x)exp(ηTT(x)−A(η))dx=1

移项:

∫ h ( x ) exp ⁡ ( η T T ( x ) ) d x = e A ( η ) \int h(x) \exp(\eta^T T(x)) \, dx = e^{A(\eta)} ∫h(x)exp(ηTT(x))dx=eA(η)

取对数:

A ( η ) = log ⁡ ∫ h ( x ) exp ⁡ ( η T T ( x ) ) d x \boxed{A(\eta) = \log \int h(x) \exp(\eta^T T(x)) \, dx} A(η)=log∫h(x)exp(ηTT(x))dx

这就是对数配分函数的显式定义。它保证了概率的归一化,但它的作用远不止于此------它的导数蕴含了分布的所有统计性质。

1.5 常见分布的指数族形式

伯努利分布 Bernoulli ( μ ) \text{Bernoulli}(\mu) Bernoulli(μ):
η = log ⁡ μ 1 − μ T ( x ) = x A ( η ) = log ⁡ ( 1 + e η ) h ( x ) = 1 \begin{aligned} \eta &= \log \frac{\mu}{1-\mu} \\ T(x) &= x \\ A(\eta) &= \log(1+e^\eta) \\ h(x) &= 1 \end{aligned} ηT(x)A(η)h(x)=log1−μμ=x=log(1+eη)=1

高斯分布 N ( μ , σ 2 ) \mathcal{N}(\mu, \sigma^2) N(μ,σ2) ( σ 2 \sigma^2 σ2 已知):
η = μ σ 2 T ( x ) = x A ( η ) = σ 2 η 2 2 h ( x ) = 1 2 π σ 2 exp ⁡ ( − x 2 2 σ 2 ) \begin{aligned} \eta &= \frac{\mu}{\sigma^2} \\ T(x) &= x \\ A(\eta) &= \frac{\sigma^2 \eta^2}{2} \\ h(x) &= \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{x^2}{2\sigma^2}\right) \end{aligned} ηT(x)A(η)h(x)=σ2μ=x=2σ2η2=2πσ2 1exp(−2σ2x2)

泊松分布 Poisson ( λ ) \text{Poisson}(\lambda) Poisson(λ):
η = log ⁡ λ T ( x ) = x A ( η ) = e η h ( x ) = 1 x ! \begin{aligned} \eta &= \log \lambda \\ T(x) &= x \\ A(\eta) &= e^\eta \\ h(x) &= \frac{1}{x!} \end{aligned} ηT(x)A(η)h(x)=logλ=x=eη=x!1

指数分布 Exp ( λ ) \text{Exp}(\lambda) Exp(λ):
η = − λ T ( x ) = x A ( η ) = − log ⁡ ( − η ) ( η < 0 ) h ( x ) = I ( x ≥ 0 ) \begin{aligned} \eta &= -\lambda \\ T(x) &= x \\ A(\eta) &= -\log(-\eta) \quad (\eta < 0) \\ h(x) &= \mathbb{I}(x \geq 0) \end{aligned} ηT(x)A(η)h(x)=−λ=x=−log(−η)(η<0)=I(x≥0)

2. 指数族分布的性质

对数配分函数 A ( η ) A(\eta) A(η) 不仅仅是归一化常数,它的导数编码了分布的所有矩信息。

2.1 一阶导数:期望

定理 1 (对数配分函数的梯度):
∇ η A ( η ) = E P ( x ∣ η ) [ T ( x ) ] \boxed{\nabla_\eta A(\eta) = \mathbb{E}_{P(x|\eta)}[T(x)]} ∇ηA(η)=EP(x∣η)[T(x)]

证明:

从 A ( η ) A(\eta) A(η) 的定义出发:

A ( η ) = log ⁡ ∫ h ( x ) exp ⁡ ( η T T ( x ) ) d x A(\eta) = \log \int h(x) \exp(\eta^T T(x)) \, dx A(η)=log∫h(x)exp(ηTT(x))dx

对 η i \eta_i ηi 求偏导。使用对数求导法则 d d x log ⁡ f ( x ) = 1 f ( x ) d f d x \frac{d}{dx}\log f(x) = \frac{1}{f(x)} \frac{df}{dx} dxdlogf(x)=f(x)1dxdf:

∂ A ( η ) ∂ η i = 1 ∫ h ( x ) exp ⁡ ( η T T ( x ) ) d x ⋅ ∂ ∂ η i ∫ h ( x ) exp ⁡ ( η T T ( x ) ) d x \frac{\partial A(\eta)}{\partial \eta_i} = \frac{1}{\int h(x) \exp(\eta^T T(x)) \, dx} \cdot \frac{\partial}{\partial \eta_i} \int h(x) \exp(\eta^T T(x)) \, dx ∂ηi∂A(η)=∫h(x)exp(ηTT(x))dx1⋅∂ηi∂∫h(x)exp(ηTT(x))dx

利用 Leibniz 积分法则,将导数穿过积分号:

∂ ∂ η i ∫ h ( x ) exp ⁡ ( η T T ( x ) ) d x = ∫ h ( x ) ∂ ∂ η i exp ⁡ ( η T T ( x ) ) d x \frac{\partial}{\partial \eta_i} \int h(x) \exp(\eta^T T(x)) \, dx = \int h(x) \frac{\partial}{\partial \eta_i} \exp(\eta^T T(x)) \, dx ∂ηi∂∫h(x)exp(ηTT(x))dx=∫h(x)∂ηi∂exp(ηTT(x))dx

计算指数函数的导数(链式法则):

∂ ∂ η i exp ⁡ ( η T T ( x ) ) = exp ⁡ ( η T T ( x ) ) ⋅ ∂ ∂ η i ( η T T ( x ) ) = exp ⁡ ( η T T ( x ) ) ⋅ T i ( x ) \frac{\partial}{\partial \eta_i} \exp(\eta^T T(x)) = \exp(\eta^T T(x)) \cdot \frac{\partial}{\partial \eta_i}(\eta^T T(x)) = \exp(\eta^T T(x)) \cdot T_i(x) ∂ηi∂exp(ηTT(x))=exp(ηTT(x))⋅∂ηi∂(ηTT(x))=exp(ηTT(x))⋅Ti(x)

因为 η T T ( x ) = ∑ j η j T j ( x ) \eta^T T(x) = \sum_j \eta_j T_j(x) ηTT(x)=∑jηjTj(x),对 η i \eta_i ηi 求导只留下 T i ( x ) T_i(x) Ti(x)。

代入:

∂ A ( η ) ∂ η i = ∫ h ( x ) T i ( x ) exp ⁡ ( η T T ( x ) ) d x ∫ h ( x ) exp ⁡ ( η T T ( x ) ) d x \frac{\partial A(\eta)}{\partial \eta_i} = \frac{\int h(x) T_i(x) \exp(\eta^T T(x)) \, dx}{\int h(x) \exp(\eta^T T(x)) \, dx} ∂ηi∂A(η)=∫h(x)exp(ηTT(x))dx∫h(x)Ti(x)exp(ηTT(x))dx

注意分母恰好是 e A ( η ) e^{A(\eta)} eA(η),分子分母同除以 e A ( η ) e^{A(\eta)} eA(η):

∂ A ( η ) ∂ η i = ∫ T i ( x ) h ( x ) exp ⁡ ( η T T ( x ) − A ( η ) ) ⏟ P ( x ∣ η ) d x = ∫ T i ( x ) P ( x ∣ η ) d x = E [ T i ( x ) ] \frac{\partial A(\eta)}{\partial \eta_i} = \int T_i(x) \underbrace{h(x) \exp(\eta^T T(x) - A(\eta))}_{P(x|\eta)} \, dx = \int T_i(x) P(x|\eta) \, dx = \mathbb{E}[T_i(x)] ∂ηi∂A(η)=∫Ti(x)P(x∣η) h(x)exp(ηTT(x)−A(η))dx=∫Ti(x)P(x∣η)dx=E[Ti(x)]

以向量形式:

∇ η A ( η ) = E [ T ( x ) ] □ \boxed{\nabla_\eta A(\eta) = \mathbb{E}[T(x)]} \quad \square ∇ηA(η)=E[T(x)]□

物理意义:

定义均值参数 (Mean Parameter):
μ = E [ T ( x ) ] \mu = \mathbb{E}[T(x)] μ=E[T(x)]

定理 1 告诉我们:
μ = ∇ η A ( η ) \mu = \nabla_\eta A(\eta) μ=∇ηA(η)

这建立了自然参数 η \eta η 和均值参数 μ \mu μ 之间的对应关系。改变 η \eta η,就改变了 μ \mu μ。

验证 :对于伯努利分布, A ( η ) = log ⁡ ( 1 + e η ) A(\eta) = \log(1+e^\eta) A(η)=log(1+eη):

d A ( η ) d η = e η 1 + e η = 1 1 + e − η = σ ( η ) = μ \frac{dA(\eta)}{d\eta} = \frac{e^\eta}{1+e^\eta} = \frac{1}{1+e^{-\eta}} = \sigma(\eta) = \mu dηdA(η)=1+eηeη=1+e−η1=σ(η)=μ

这正是 sigmoid 函数!自然参数 η ∈ R \eta \in \mathbb{R} η∈R 通过 sigmoid 映射到概率 μ ∈ ( 0 , 1 ) \mu \in (0,1) μ∈(0,1)。

2.2 二阶导数:方差

定理 2 (对数配分函数的 Hessian):
∇ η 2 A ( η ) = Cov [ T ( x ) ] \boxed{\nabla^2_\eta A(\eta) = \text{Cov}[T(x)]} ∇η2A(η)=Cov[T(x)]

其中 Hessian 矩阵的 ( i , j ) (i,j) (i,j) 元素为:

∇ η 2 A ( η ) \] i j = ∂ 2 A ( η ) ∂ η i ∂ η j \\left\[\\nabla\^2_\\eta A(\\eta)\\right\]_{ij} = \\frac{\\partial\^2 A(\\eta)}{\\partial \\eta_i \\partial \\eta_j} \[∇η2A(η)\]ij=∂ηi∂ηj∂2A(η) 协方差矩阵定义为: Cov \[ T ( x ) \] i j = E \[ T i ( x ) T j ( x ) \] − E \[ T i ( x ) \] E \[ T j ( x ) \] \\text{Cov}\[T(x)\]_{ij} = \\mathbb{E}\[T_i(x) T_j(x)\] - \\mathbb{E}\[T_i(x)\] \\mathbb{E}\[T_j(x)\] Cov\[T(x)\]ij=E\[Ti(x)Tj(x)\]−E\[Ti(x)\]E\[Tj(x)

证明:

从定理 1 我们知道:

∂ A ( η ) ∂ η i = E [ T i ( x ) ] = ∫ T i ( x ) P ( x ∣ η ) d x \frac{\partial A(\eta)}{\partial \eta_i} = \mathbb{E}[T_i(x)] = \int T_i(x) P(x|\eta) \, dx ∂ηi∂A(η)=E[Ti(x)]=∫Ti(x)P(x∣η)dx

对 η j \eta_j ηj 再次求导:

∂ 2 A ( η ) ∂ η i ∂ η j = ∂ ∂ η j ∫ T i ( x ) P ( x ∣ η ) d x = ∫ T i ( x ) ∂ P ( x ∣ η ) ∂ η j d x \frac{\partial^2 A(\eta)}{\partial \eta_i \partial \eta_j} = \frac{\partial}{\partial \eta_j} \int T_i(x) P(x|\eta) \, dx = \int T_i(x) \frac{\partial P(x|\eta)}{\partial \eta_j} \, dx ∂ηi∂ηj∂2A(η)=∂ηj∂∫Ti(x)P(x∣η)dx=∫Ti(x)∂ηj∂P(x∣η)dx

关键是计算 ∂ P ( x ∣ η ) ∂ η j \frac{\partial P(x|\eta)}{\partial \eta_j} ∂ηj∂P(x∣η)。从 P ( x ∣ η ) = h ( x ) exp ⁡ ( η T T ( x ) − A ( η ) ) P(x|\eta) = h(x) \exp(\eta^T T(x) - A(\eta)) P(x∣η)=h(x)exp(ηTT(x)−A(η)),取对数:

log ⁡ P ( x ∣ η ) = log ⁡ h ( x ) + η T T ( x ) − A ( η ) \log P(x|\eta) = \log h(x) + \eta^T T(x) - A(\eta) logP(x∣η)=logh(x)+ηTT(x)−A(η)

对 η j \eta_j ηj 求导:

∂ log ⁡ P ( x ∣ η ) ∂ η j = T j ( x ) − ∂ A ( η ) ∂ η j = T j ( x ) − E [ T j ( x ) ] \frac{\partial \log P(x|\eta)}{\partial \eta_j} = T_j(x) - \frac{\partial A(\eta)}{\partial \eta_j} = T_j(x) - \mathbb{E}[T_j(x)] ∂ηj∂logP(x∣η)=Tj(x)−∂ηj∂A(η)=Tj(x)−E[Tj(x)]

利用对数导数技巧 ∂ P ∂ η j = P ∂ log ⁡ P ∂ η j \frac{\partial P}{\partial \eta_j} = P \frac{\partial \log P}{\partial \eta_j} ∂ηj∂P=P∂ηj∂logP:

∂ P ( x ∣ η ) ∂ η j = P ( x ∣ η ) [ T j ( x ) − E [ T j ( x ) ] ] \frac{\partial P(x|\eta)}{\partial \eta_j} = P(x|\eta) \left[T_j(x) - \mathbb{E}[T_j(x)]\right] ∂ηj∂P(x∣η)=P(x∣η)[Tj(x)−E[Tj(x)]]

代入二阶导数:

∂ 2 A ( η ) ∂ η i ∂ η j = ∫ T i ( x ) P ( x ∣ η ) [ T j ( x ) − E [ T j ( x ) ] ] d x \frac{\partial^2 A(\eta)}{\partial \eta_i \partial \eta_j} = \int T_i(x) P(x|\eta) \left[T_j(x) - \mathbb{E}[T_j(x)]\right] \, dx ∂ηi∂ηj∂2A(η)=∫Ti(x)P(x∣η)[Tj(x)−E[Tj(x)]]dx

展开:

= ∫ T i ( x ) T j ( x ) P ( x ∣ η ) d x − ∫ T i ( x ) P ( x ∣ η ) d x ⋅ E [ T j ( x ) ] = E [ T i ( x ) T j ( x ) ] − E [ T i ( x ) ] E [ T j ( x ) ] = Cov [ T i ( x ) , T j ( x ) ] \begin{aligned} &= \int T_i(x) T_j(x) P(x|\eta) \, dx - \int T_i(x) P(x|\eta) \, dx \cdot \mathbb{E}[T_j(x)] \\ &= \mathbb{E}[T_i(x) T_j(x)] - \mathbb{E}[T_i(x)] \mathbb{E}[T_j(x)] \\ &= \text{Cov}[T_i(x), T_j(x)] \end{aligned} =∫Ti(x)Tj(x)P(x∣η)dx−∫Ti(x)P(x∣η)dx⋅E[Tj(x)]=E[Ti(x)Tj(x)]−E[Ti(x)]E[Tj(x)]=Cov[Ti(x),Tj(x)]

因此:

∇ η 2 A ( η ) = Cov [ T ( x ) ] □ \boxed{\nabla^2_\eta A(\eta) = \text{Cov}[T(x)]} \quad \square ∇η2A(η)=Cov[T(x)]□

物理意义:

协方差矩阵总是半正定的 ( Cov [ T ( x ) ] ⪰ 0 \text{Cov}[T(x)] \succeq 0 Cov[T(x)]⪰0),因此:

∇ η 2 A ( η ) ⪰ 0 \nabla^2_\eta A(\eta) \succeq 0 ∇η2A(η)⪰0

这意味着 A ( η ) A(\eta) A(η) 是凸函数。

推论 (凸性的后果):

负对数似然 − log ⁡ P ( x ∣ η ) = A ( η ) − η T T ( x ) + const -\log P(x|\eta) = A(\eta) - \eta^T T(x) + \text{const} −logP(x∣η)=A(η)−ηTT(x)+const 是关于 η \eta η 的凸函数
最大似然估计 (MLE) 是凸优化问题
MLE 的解存在且唯一 (在参数空间内部)
梯度下降必然收敛到全局最优

这是指数族分布的第一个核心优势:优化问题天然是凸的。

2.3 Fisher 信息矩阵

定义 Fisher 信息矩阵:

I ( η ) = E [ ( ∇ η log ⁡ P ( x ∣ η ) ) ( ∇ η log ⁡ P ( x ∣ η ) ) T ] \mathcal{I}(\eta) = \mathbb{E}\left[\left(\nabla_\eta \log P(x|\eta)\right) \left(\nabla_\eta \log P(x|\eta)\right)^T\right] I(η)=E[(∇ηlogP(x∣η))(∇ηlogP(x∣η))T]

它度量参数 η \eta η 的可估计性:Fisher 信息越大,参数越容易从数据中估计。

对于指数族分布:

∇ η log ⁡ P ( x ∣ η ) = ∇ η [ η T T ( x ) − A ( η ) ] = T ( x ) − ∇ η A ( η ) = T ( x ) − E [ T ( x ) ] \nabla_\eta \log P(x|\eta) = \nabla_\eta \left[\eta^T T(x) - A(\eta)\right] = T(x) - \nabla_\eta A(\eta) = T(x) - \mathbb{E}[T(x)] ∇ηlogP(x∣η)=∇η[ηTT(x)−A(η)]=T(x)−∇ηA(η)=T(x)−E[T(x)]

因此:

I ( η ) = E [ ( T ( x ) − E [ T ( x ) ] ) ( T ( x ) − E [ T ( x ) ] ) T ] = Cov [ T ( x ) ] \begin{aligned} \mathcal{I}(\eta) &= \mathbb{E}\left[(T(x) - \mathbb{E}[T(x)])(T(x) - \mathbb{E}[T(x)])^T\right] \\ &= \text{Cov}[T(x)] \end{aligned} I(η)=E[(T(x)−E[T(x)])(T(x)−E[T(x)])T]=Cov[T(x)]

结合定理 2:

I ( η ) = ∇ η 2 A ( η ) \boxed{\mathcal{I}(\eta) = \nabla^2_\eta A(\eta)} I(η)=∇η2A(η)

意义 : Fisher 信息矩阵等于对数配分函数的 Hessian。这意味着 A ( η ) A(\eta) A(η) 的曲率直接编码了参数的可估计性:曲率越大 (方差越大),参数越难估计,需要更多数据。

2.4 最大似然估计的矩匹配

对于 i.i.d. 样本 { x 1 , ... , x N } \{x_1, \ldots, x_N\} {x1,...,xN},对数似然为:

ℓ ( η ) = ∑ i = 1 N log ⁡ P ( x i ∣ η ) = ∑ i = 1 N [ η T T ( x i ) − A ( η ) + log ⁡ h ( x i ) ] \ell(\eta) = \sum_{i=1}^N \log P(x_i|\eta) = \sum_{i=1}^N \left[\eta^T T(x_i) - A(\eta) + \log h(x_i)\right] ℓ(η)=i=1∑NlogP(xi∣η)=i=1∑N[ηTT(xi)−A(η)+logh(xi)]

去掉与 η \eta η 无关的项:

ℓ ( η ) = N η T T ˉ − N A ( η ) + const \ell(\eta) = N \eta^T \bar{T} - N A(\eta) + \text{const} ℓ(η)=NηTTˉ−NA(η)+const

其中 T ˉ = 1 N ∑ i = 1 N T ( x i ) \bar{T} = \frac{1}{N}\sum_{i=1}^N T(x_i) Tˉ=N1∑i=1NT(xi) 是充分统计量的样本均值。

一阶最优条件:

∇ η ℓ ( η ) = N T ˉ − N ∇ η A ( η ) = 0 \nabla_\eta \ell(\eta) = N \bar{T} - N \nabla_\eta A(\eta) = 0 ∇ηℓ(η)=NTˉ−N∇ηA(η)=0

即:

∇ η A ( η ^ MLE ) = T ˉ \boxed{\nabla_\eta A(\hat{\eta}_{\text{MLE}}) = \bar{T}} ∇ηA(η^MLE)=Tˉ

结合定理 1:

E P ( x ∣ η ^ MLE ) [ T ( x ) ] = T ˉ \boxed{\mathbb{E}{P(x|\hat{\eta}{\text{MLE}})}[T(x)] = \bar{T}} EP(x∣η^MLE)[T(x)]=Tˉ

MLE 的物理意义 : 最大似然估计使得模型的理论期望等于数据的经验期望 。这称为矩匹配 (Moment Matching)。

例子 (伯努利分布):

T ( x ) = x T(x) = x T(x)=x, T ˉ = 1 N ∑ i = 1 N x i = μ ^ \bar{T} = \frac{1}{N}\sum_{i=1}^N x_i = \hat{\mu} Tˉ=N1∑i=1Nxi=μ^ (样本均值)。

MLE 条件:

∇ η A ( η ) = σ ( η ) = μ ^ \nabla_\eta A(\eta) = \sigma(\eta) = \hat{\mu} ∇ηA(η)=σ(η)=μ^

解得:

η ^ MLE = logit ( μ ^ ) = log ⁡ μ ^ 1 − μ ^ \hat{\eta}_{\text{MLE}} = \text{logit}(\hat{\mu}) = \log \frac{\hat{\mu}}{1-\hat{\mu}} η^MLE=logit(μ^)=log1−μ^μ^

这正是我们期望的结果。

3. 指数族分布与最大熵

3.1 问题:如何选择概率分布?

假设我们对一个随机变量 x x x 一无所知,只知道某些统计量的期望值:

E [ T k ( x ) ] = α k , k = 1 , ... , m \mathbb{E}[T_k(x)] = \alpha_k, \quad k = 1, \ldots, m E[Tk(x)]=αk,k=1,...,m

例如:

只知道均值 E [ x ] = μ \mathbb{E}[x] = \mu E[x]=μ
只知道均值和二阶矩 E [ x ] = μ , E [ x 2 ] = σ 2 + μ 2 \mathbb{E}[x] = \mu, \mathbb{E}[x^2] = \sigma^2 + \mu^2 E[x]=μ,E[x2]=σ2+μ2

问题: 在满足这些约束的所有概率分布中,我们应该选择哪一个?

答案 : 选择熵最大的分布。

3.2 熵与最大熵原理

Shannon 熵定义为:

H [ P ] = − ∫ P ( x ) log ⁡ P ( x ) d x H[P] = -\int P(x) \log P(x) \, dx H[P]=−∫P(x)logP(x)dx

熵度量分布的"不确定性":

均匀分布:熵最大 (最不确定)
Dirac delta 函数:熵为 0 (完全确定)

最大熵原理 (Maximum Entropy Principle):

在满足已知约束的前提下,选择熵最大的分布。

哲学依据 : 这是"奥卡姆剃刀"的概率版本------不要假设你不知道的东西。给定约束,选择最"无偏"、最"保守"的分布,不引入任何额外的假设。

3.3 推导:最大熵分布是指数族

优化问题:

max ⁡ P ( x ) H [ P ] = − ∫ P ( x ) log ⁡ P ( x ) d x s.t. ∫ P ( x ) d x = 1 ∫ P ( x ) T k ( x ) d x = α k , k = 1 , ... , m \begin{aligned} \max_{P(x)} \quad & H[P] = -\int P(x) \log P(x) \, dx \\ \text{s.t.} \quad & \int P(x) \, dx = 1 \\ & \int P(x) T_k(x) \, dx = \alpha_k, \quad k = 1, \ldots, m \end{aligned} P(x)maxs.t.H[P]=−∫P(x)logP(x)dx∫P(x)dx=1∫P(x)Tk(x)dx=αk,k=1,...,m

构造 Lagrange 泛函:

L [ P ] = − ∫ P ( x ) log ⁡ P ( x ) d x + λ 0 ( ∫ P ( x ) d x − 1 ) + ∑ k = 1 m λ k ( ∫ P ( x ) T k ( x ) d x − α k ) \mathcal{L}[P] = -\int P(x) \log P(x) \, dx + \lambda_0 \left(\int P(x) \, dx - 1\right) + \sum_{k=1}^m \lambda_k \left(\int P(x) T_k(x) \, dx - \alpha_k\right) L[P]=−∫P(x)logP(x)dx+λ0(∫P(x)dx−1)+k=1∑mλk(∫P(x)Tk(x)dx−αk)

对 P ( x ) P(x) P(x) 做变分 (泛函导数):

δ L δ P ( x ) = − log ⁡ P ( x ) − 1 + λ 0 + ∑ k = 1 m λ k T k ( x ) \frac{\delta \mathcal{L}}{\delta P(x)} = -\log P(x) - 1 + \lambda_0 + \sum_{k=1}^m \lambda_k T_k(x) δP(x)δL=−logP(x)−1+λ0+k=1∑mλkTk(x)

令变分为零:

− log ⁡ P ( x ) − 1 + λ 0 + ∑ k = 1 m λ k T k ( x ) = 0 -\log P(x) - 1 + \lambda_0 + \sum_{k=1}^m \lambda_k T_k(x) = 0 −logP(x)−1+λ0+k=1∑mλkTk(x)=0

解出 log ⁡ P ( x ) \log P(x) logP(x):

log ⁡ P ( x ) = − 1 + λ 0 + ∑ k = 1 m λ k T k ( x ) \log P(x) = -1 + \lambda_0 + \sum_{k=1}^m \lambda_k T_k(x) logP(x)=−1+λ0+k=1∑mλkTk(x)

指数化:

P ( x ) = exp ⁡ ( − 1 + λ 0 + ∑ k = 1 m λ k T k ( x ) ) = e λ 0 − 1 exp ⁡ ( ∑ k = 1 m λ k T k ( x ) ) P(x) = \exp\left(-1 + \lambda_0 + \sum_{k=1}^m \lambda_k T_k(x)\right) = e^{\lambda_0 - 1} \exp\left(\sum_{k=1}^m \lambda_k T_k(x)\right) P(x)=exp(−1+λ0+k=1∑mλkTk(x))=eλ0−1exp(k=1∑mλkTk(x))

利用归一化条件 ∫ P ( x ) d x = 1 \int P(x) \, dx = 1 ∫P(x)dx=1 确定常数项。定义:

A ( λ ) = 1 − λ 0 = log ⁡ ∫ exp ⁡ ( ∑ k = 1 m λ k T k ( x ) ) d x A(\lambda) = 1 - \lambda_0 = \log \int \exp\left(\sum_{k=1}^m \lambda_k T_k(x)\right) dx A(λ)=1−λ0=log∫exp(k=1∑mλkTk(x))dx

最终得到:

P ( x ) = exp ⁡ ( ∑ k = 1 m λ k T k ( x ) − A ( λ ) ) P(x) = \exp\left(\sum_{k=1}^m \lambda_k T_k(x) - A(\lambda)\right) P(x)=exp(k=1∑mλkTk(x)−A(λ))

这正是指数族分布的标准形式 (取 h ( x ) = 1 h(x) = 1 h(x)=1, η = λ \eta = \lambda η=λ)!

结论:

最大熵分布 = 指数族分布 \boxed{\text{最大熵分布} = \text{指数族分布}} 最大熵分布=指数族分布

Lagrange 乘子 λ \lambda λ 对应自然参数 η \eta η。 □ \square □

意义:

指数族分布不是人为构造的,而是信息论的必然结果。给定矩约束,指数族是唯一最保守的选择。

3.4 例子 1:高斯分布

约束:只知道均值和方差,

E [ x ] = μ , E [ x 2 ] = σ 2 + μ 2 \mathbb{E}[x] = \mu, \quad \mathbb{E}[x^2] = \sigma^2 + \mu^2 E[x]=μ,E[x2]=σ2+μ2

充分统计量:

T ( x ) = [ x x 2 ] T(x) = \begin{bmatrix} x \\ x^2 \end{bmatrix} T(x)=[xx2]

最大熵分布:

P ( x ) = exp ⁡ ( λ 1 x + λ 2 x 2 − A ( λ ) ) P(x) = \exp(\lambda_1 x + \lambda_2 x^2 - A(\lambda)) P(x)=exp(λ1x+λ2x2−A(λ))

配方:

λ 2 x 2 + λ 1 x = λ 2 ( x + λ 1 2 λ 2 ) 2 − λ 1 2 4 λ 2 \lambda_2 x^2 + \lambda_1 x = \lambda_2 \left(x + \frac{\lambda_1}{2\lambda_2}\right)^2 - \frac{\lambda_1^2}{4\lambda_2} λ2x2+λ1x=λ2(x+2λ2λ1)2−4λ2λ12

要使其是有效概率分布 (可积),必须 λ 2 < 0 \lambda_2 < 0 λ2<0。设:

λ 2 = − 1 2 σ 2 , λ 1 = μ σ 2 \lambda_2 = -\frac{1}{2\sigma^2}, \quad \lambda_1 = \frac{\mu}{\sigma^2} λ2=−2σ21,λ1=σ2μ

代入并整理,得到:

P ( x ) = 1 2 π σ 2 exp ⁡ ( − ( x − μ ) 2 2 σ 2 ) P(x) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right) P(x)=2πσ2 1exp(−2σ2(x−μ)2)

结论: 高斯分布是给定均值和方差的最大熵分布。

物理意义 : 如果你只知道一个随机变量的均值和方差,你能做的最保守假设就是它服从高斯分布。这就是为什么高斯分布无处不在------不是因为自然"喜欢"高斯,而是因为我们通常只掌握有限的矩信息。

3.5 例子 2:指数分布

约束 (假设 x ≥ 0 x \geq 0 x≥0):

E [ x ] = μ \mathbb{E}[x] = \mu E[x]=μ

充分统计量:

T ( x ) = x T(x) = x T(x)=x

最大熵分布:

P ( x ) = exp ⁡ ( λ x − A ( λ ) ) P(x) = \exp(\lambda x - A(\lambda)) P(x)=exp(λx−A(λ))

归一化:

A ( λ ) = log ⁡ ∫ 0 ∞ exp ⁡ ( λ x ) d x A(\lambda) = \log \int_0^\infty \exp(\lambda x) \, dx A(λ)=log∫0∞exp(λx)dx

为使积分收敛,必须 λ < 0 \lambda < 0 λ<0。设 λ = − 1 / μ \lambda = -1/\mu λ=−1/μ,则:

∫ 0 ∞ exp ⁡ ( − x / μ ) d x = μ \int_0^\infty \exp(-x/\mu) \, dx = \mu ∫0∞exp(−x/μ)dx=μ

因此:

A ( λ ) = log ⁡ μ = − log ⁡ ( − λ ) A(\lambda) = \log \mu = -\log(-\lambda) A(λ)=logμ=−log(−λ)

最终分布:

P ( x ) = 1 μ exp ⁡ ( − x μ ) P(x) = \frac{1}{\mu} \exp\left(-\frac{x}{\mu}\right) P(x)=μ1exp(−μx)

这是指数分布 Exp ( 1 / μ ) \text{Exp}(1/\mu) Exp(1/μ)。

物理意义: 如果你只知道一个非负随机变量的均值,指数分布是最保守的选择。这解释了为什么等待时间、寿命等常服从指数分布------当我们对过程的细节一无所知时,指数分布是最自然的选择。

3.6 例子 3:离散均匀分布

约束:无约束 (除了归一化)。

在有限集合 { x 1 , ... , x n } \{x_1, \ldots, x_n\} {x1,...,xn} 上,最大熵分布是:

P ( x i ) = 1 n , i = 1 , ... , n P(x_i) = \frac{1}{n}, \quad i = 1, \ldots, n P(xi)=n1,i=1,...,n

这是离散均匀分布。

物理意义: 如果你对一个离散随机变量一无所知,最保守的假设就是等概率。

4. 指数族分布与广义线性模型 (GLM)

4.1 问题:线性回归与逻辑回归的统一

看看两个经典模型:

线性回归:

模型: y ∣ x ∼ N ( w T x , σ 2 ) y|x \sim \mathcal{N}(w^T x, \sigma^2) y∣x∼N(wTx,σ2)
损失函数:最小二乘 ∑ ( y i − w T x i ) 2 \sum (y_i - w^T x_i)^2 ∑(yi−wTxi)2

逻辑回归:

模型: y ∣ x ∼ Bernoulli ( σ ( w T x ) ) y|x \sim \text{Bernoulli}(\sigma(w^T x)) y∣x∼Bernoulli(σ(wTx))
损失函数:交叉熵 − ∑ [ y i log ⁡ σ ( w T x i ) + ( 1 − y i ) log ⁡ ( 1 − σ ( w T x i ) ) ] -\sum [y_i \log \sigma(w^T x_i) + (1-y_i) \log(1-\sigma(w^T x_i))] −∑[yilogσ(wTxi)+(1−yi)log(1−σ(wTxi))]

它们看起来完全不同!损失函数的形式天差地别。

但它们本质相同------都是广义线性模型 (Generalized Linear Model, GLM)。

4.2 GLM 的定义

广义线性模型由三部分组成:

1. 随机成分 : 响应变量 y y y 服从指数族分布

P ( y ∣ x , w ) = h ( y ) exp ⁡ ( η ( x , w ) ⋅ y − A ( η ( x , w ) ) ) P(y|x, w) = h(y) \exp\left(\eta(x, w) \cdot y - A(\eta(x, w))\right) P(y∣x,w)=h(y)exp(η(x,w)⋅y−A(η(x,w)))

这里假设 T ( y ) = y T(y) = y T(y)=y,称为规范形式 (Canonical Form)。

2. 系统成分: 自然参数是输入的线性函数

η ( x , w ) = w T x \eta(x, w) = w^T x η(x,w)=wTx

3. 连接函数 : 自然参数 η \eta η 与均值 μ = E [ y ∣ x ] \mu = \mathbb{E}[y|x] μ=E[y∣x] 的关系

由定理 1:

μ = ∇ η A ( η ) \mu = \nabla_\eta A(\eta) μ=∇ηA(η)

定义连接函数 g g g:

η = g ( μ ) \eta = g(\mu) η=g(μ)

若 g g g 使得 η = w T x \eta = w^T x η=wTx 直接对应自然参数化,称为规范连接 (Canonical Link)。对于规范形式的指数族,规范连接就是 g = ( ∇ η A ) − 1 g = (\nabla_\eta A)^{-1} g=(∇ηA)−1。

4.3 核心推导:GLM 的统一梯度公式

这是本章最激动人心的推导:无论分布是什么,梯度公式都一样。

给定数据 { ( x i , y i ) } i = 1 N \{(x_i, y_i)\}_{i=1}^N {(xi,yi)}i=1N,负对数似然为:

L ( w ) = − ∑ i = 1 N log ⁡ P ( y i ∣ x i , w ) = − ∑ i = 1 N [ η i y i − A ( η i ) + log ⁡ h ( y i ) ] \mathcal{L}(w) = -\sum_{i=1}^N \log P(y_i|x_i, w) = -\sum_{i=1}^N \left[\eta_i y_i - A(\eta_i) + \log h(y_i)\right] L(w)=−i=1∑NlogP(yi∣xi,w)=−i=1∑N[ηiyi−A(ηi)+logh(yi)]

其中 η i = w T x i \eta_i = w^T x_i ηi=wTxi。去掉与 w w w 无关的项:

L ( w ) = − ∑ i = 1 N [ w T x i ⋅ y i − A ( w T x i ) ] + const \mathcal{L}(w) = -\sum_{i=1}^N \left[w^T x_i \cdot y_i - A(w^T x_i)\right] + \text{const} L(w)=−i=1∑N[wTxi⋅yi−A(wTxi)]+const

对 w w w 求梯度,使用链式法则:

∇ w L ( w ) = − ∑ i = 1 N [ y i x i − ∂ A ( η i ) ∂ η i ⋅ ∂ η i ∂ w ] \nabla_w \mathcal{L}(w) = -\sum_{i=1}^N \left[y_i x_i - \frac{\partial A(\eta_i)}{\partial \eta_i} \cdot \frac{\partial \eta_i}{\partial w}\right] ∇wL(w)=−i=1∑N[yixi−∂ηi∂A(ηi)⋅∂w∂ηi]

注意:

∂ η i ∂ w = ∂ ( w T x i ) ∂ w = x i \frac{\partial \eta_i}{\partial w} = \frac{\partial (w^T x_i)}{\partial w} = x_i ∂w∂ηi=∂w∂(wTxi)=xi
∂ A ( η i ) ∂ η i = E [ y i ∣ x i ] = μ i \frac{\partial A(\eta_i)}{\partial \eta_i} = \mathbb{E}[y_i|x_i] = \mu_i ∂ηi∂A(ηi)=E[yi∣xi]=μi (由定理 1)

代入:

∇ w L ( w ) = − ∑ i = 1 N ( y i − μ i ) x i \nabla_w \mathcal{L}(w) = -\sum_{i=1}^N (y_i - \mu_i) x_i ∇wL(w)=−i=1∑N(yi−μi)xi

GLM 的核心公式:

∇ w L ( w ) = − ∑ i = 1 N ( y i − μ i ) x i \boxed{\nabla_w \mathcal{L}(w) = -\sum_{i=1}^N (y_i - \mu_i) x_i} ∇wL(w)=−i=1∑N(yi−μi)xi

其中 μ i = E [ y i ∣ x i ] = ∇ η A ( η i ) ∣ η i = w T x i \mu_i = \mathbb{E}[y_i|x_i] = \nabla_\eta A(\eta_i)|_{\eta_i = w^T x_i} μi=E[yi∣xi]=∇ηA(ηi)∣ηi=wTxi。

公式的物理意义:

∇ w L ( w ) = − ∑ i = 1 N ( y i − μ i ) ⏟ 残差 ⋅ x i ⏟ 特征 \nabla_w \mathcal{L}(w) = -\sum_{i=1}^N \underbrace{(y_i - \mu_i)}{\text{残差}} \cdot \underbrace{x_i}{\text{特征}} ∇wL(w)=−i=1∑N残差 (yi−μi)⋅特征 xi

梯度是残差与特征的加权和。

关键观察: 无论分布是什么 (高斯、伯努利、泊松),梯度都是这个形式!唯一的差异在于:

μ i = ∇ η A ( η i ) \mu_i = \nabla_\eta A(\eta_i) μi=∇ηA(ηi) 的具体计算
而这由对数配分函数 A ( η ) A(\eta) A(η) 完全决定

这不仅仅是巧合------这是指数族分布的几何本质。对数配分函数的导数性质统一了所有回归模型的优化。

4.4 Hessian 矩阵:凸性保证

继续对梯度求导:

∇ w 2 L ( w ) = ∑ i = 1 N ∂ μ i ∂ w x i T \nabla^2_w \mathcal{L}(w) = \sum_{i=1}^N \frac{\partial \mu_i}{\partial w} x_i^T ∇w2L(w)=i=1∑N∂w∂μixiT

使用链式法则:

∂ μ i ∂ w = ∂ μ i ∂ η i ⋅ ∂ η i ∂ w = ∂ μ i ∂ η i ⋅ x i \frac{\partial \mu_i}{\partial w} = \frac{\partial \mu_i}{\partial \eta_i} \cdot \frac{\partial \eta_i}{\partial w} = \frac{\partial \mu_i}{\partial \eta_i} \cdot x_i ∂w∂μi=∂ηi∂μi⋅∂w∂ηi=∂ηi∂μi⋅xi

注意 μ i = ∇ η A ( η i ) \mu_i = \nabla_\eta A(\eta_i) μi=∇ηA(ηi),因此:

∂ μ i ∂ η i = ∇ η 2 A ( η i ) = Var [ y i ∣ x i ] \frac{\partial \mu_i}{\partial \eta_i} = \nabla^2_\eta A(\eta_i) = \text{Var}[y_i|x_i] ∂ηi∂μi=∇η2A(ηi)=Var[yi∣xi]

(由定理 2,对于标量情况协方差就是方差)

代入:

∇ w 2 L ( w ) = ∑ i = 1 N Var [ y i ∣ x i ] ⋅ x i x i T \nabla^2_w \mathcal{L}(w) = \sum_{i=1}^N \text{Var}[y_i|x_i] \cdot x_i x_i^T ∇w2L(w)=i=1∑NVar[yi∣xi]⋅xixiT

以矩阵形式:

∇ w 2 L ( w ) = X T W X \nabla^2_w \mathcal{L}(w) = X^T W X ∇w2L(w)=XTWX

其中:

X ∈ R N × d X \in \mathbb{R}^{N \times d} X∈RN×d 是设计矩阵 (第 i i i 行是 x i T x_i^T xiT)
W = diag ( Var [ y 1 ∣ x 1 ] , ... , Var [ y N ∣ x N ] ) ∈ R N × N W = \text{diag}(\text{Var}[y_1|x_1], \ldots, \text{Var}[y_N|x_N]) \in \mathbb{R}^{N \times N} W=diag(Var[y1∣x1],...,Var[yN∣xN])∈RN×N 是权重矩阵

凸性:

因为方差 Var [ y i ∣ x i ] > 0 \text{Var}[y_i|x_i] > 0 Var[yi∣xi]>0,且假设 X X X 列满秩,Hessian 正定:

∇ w 2 L ( w ) ≻ 0 \nabla^2_w \mathcal{L}(w) \succ 0 ∇w2L(w)≻0

因此:

L ( w ) 是严格凸函数 \boxed{\mathcal{L}(w) \text{ 是严格凸函数}} L(w) 是严格凸函数

推论:

MLE 存在且唯一
梯度下降保证收敛到全局最优
无局部最优问题

这是指数族分布送给统计学习的第二个礼物 (第一个是统一的梯度公式)。

4.5 例子 1:线性回归 (高斯 GLM)

模型 : y ∣ x ∼ N ( w T x , σ 2 ) y|x \sim \mathcal{N}(w^T x, \sigma^2) y∣x∼N(wTx,σ2)

指数族参数:

自然参数: η = w T x \eta = w^T x η=wTx
对数配分函数: A ( η ) = σ 2 η 2 2 A(\eta) = \frac{\sigma^2 \eta^2}{2} A(η)=2σ2η2
均值参数: μ = ∇ η A ( η ) = σ 2 η = w T x \mu = \nabla_\eta A(\eta) = \sigma^2 \eta = w^T x μ=∇ηA(η)=σ2η=wTx

梯度:

∇ w L ( w ) = − ∑ i = 1 N ( y i − w T x i ) x i \nabla_w \mathcal{L}(w) = -\sum_{i=1}^N (y_i - w^T x_i) x_i ∇wL(w)=−i=1∑N(yi−wTxi)xi

这正是最小二乘的梯度!

Hessian:

Var [ y i ∣ x i ] = σ 2 ( 常数 ) \text{Var}[y_i|x_i] = \sigma^2 \quad (\text{常数}) Var[yi∣xi]=σ2(常数)

因此:

∇ w 2 L ( w ) = σ 2 X T X \nabla^2_w \mathcal{L}(w) = \sigma^2 X^T X ∇w2L(w)=σ2XTX

这正是线性回归的 Hessian。

4.6 例子 2:逻辑回归 (伯努利 GLM)

模型 : y ∣ x ∼ Bernoulli ( σ ( w T x ) ) y|x \sim \text{Bernoulli}(\sigma(w^T x)) y∣x∼Bernoulli(σ(wTx))

指数族参数:

自然参数: η = w T x \eta = w^T x η=wTx
对数配分函数: A ( η ) = log ⁡ ( 1 + e η ) A(\eta) = \log(1 + e^\eta) A(η)=log(1+eη)
均值参数: μ = ∇ η A ( η ) = e η 1 + e η = σ ( η ) = σ ( w T x ) \mu = \nabla_\eta A(\eta) = \frac{e^\eta}{1+e^\eta} = \sigma(\eta) = \sigma(w^T x) μ=∇ηA(η)=1+eηeη=σ(η)=σ(wTx)

梯度:

∇ w L ( w ) = − ∑ i = 1 N ( y i − σ ( w T x i ) ) x i \nabla_w \mathcal{L}(w) = -\sum_{i=1}^N (y_i - \sigma(w^T x_i)) x_i ∇wL(w)=−i=1∑N(yi−σ(wTxi))xi

这正是逻辑回归的梯度!

Hessian:

Var [ y i ∣ x i ] = μ i ( 1 − μ i ) = σ ( w T x i ) ( 1 − σ ( w T x i ) ) \text{Var}[y_i|x_i] = \mu_i(1-\mu_i) = \sigma(w^T x_i)(1-\sigma(w^T x_i)) Var[yi∣xi]=μi(1−μi)=σ(wTxi)(1−σ(wTxi))

因此:

∇ w 2 L ( w ) = X T W X , W = diag ( μ 1 ( 1 − μ 1 ) , ... , μ N ( 1 − μ N ) ) \nabla^2_w \mathcal{L}(w) = X^T W X, \quad W = \text{diag}(\mu_1(1-\mu_1), \ldots, \mu_N(1-\mu_N)) ∇w2L(w)=XTWX,W=diag(μ1(1−μ1),...,μN(1−μN))

这正是逻辑回归的 Hessian (也是 IRLS 算法的权重矩阵)。

4.7 例子 3:泊松回归 (泊松 GLM)

模型 : y ∣ x ∼ Poisson ( e w T x ) y|x \sim \text{Poisson}(e^{w^T x}) y∣x∼Poisson(ewTx)

指数族参数:

自然参数: η = w T x \eta = w^T x η=wTx
对数配分函数: A ( η ) = e η A(\eta) = e^\eta A(η)=eη
均值参数: μ = ∇ η A ( η ) = e η = e w T x \mu = \nabla_\eta A(\eta) = e^\eta = e^{w^T x} μ=∇ηA(η)=eη=ewTx

梯度:

∇ w L ( w ) = − ∑ i = 1 N ( y i − e w T x i ) x i \nabla_w \mathcal{L}(w) = -\sum_{i=1}^N (y_i - e^{w^T x_i}) x_i ∇wL(w)=−i=1∑N(yi−ewTxi)xi

Hessian:

Var [ y i ∣ x i ] = μ i = e w T x i \text{Var}[y_i|x_i] = \mu_i = e^{w^T x_i} Var[yi∣xi]=μi=ewTxi

因此:

∇ w 2 L ( w ) = X T W X , W = diag ( e w T x 1 , ... , e w T x N ) \nabla^2_w \mathcal{L}(w) = X^T W X, \quad W = \text{diag}(e^{w^T x_1}, \ldots, e^{w^T x_N}) ∇w2L(w)=XTWX,W=diag(ewTx1,...,ewTxN)

4.8 GLM 的几何理解

所有 GLM 都在做同一件事:

通过线性组合 w T x w^T x wTx 构造自然参数 η \eta η
通过 μ = ∇ η A ( η ) \mu = \nabla_\eta A(\eta) μ=∇ηA(η) 将 η \eta η 映射到均值参数空间
优化目标是最小化观测值 y y y 与预测均值 μ \mu μ 之间的"距离"

不同的 GLM 只是选择了不同的分布 (即不同的 A ( η ) A(\eta) A(η)),从而对应不同的均值-方差关系:

高斯: Var [ y ∣ x ] = σ 2 \text{Var}[y|x] = \sigma^2 Var[y∣x]=σ2 (常数)
伯努利: Var [ y ∣ x ] = μ ( 1 − μ ) \text{Var}[y|x] = \mu(1-\mu) Var[y∣x]=μ(1−μ) (二次函数)
泊松: Var [ y ∣ x ] = μ \text{Var}[y|x] = \mu Var[y∣x]=μ (均值-方差相等)

但优化的本质是相同的:所有 GLM 的梯度都是残差与特征的线性组合。

5. 总结

5.1 主要结论

1. 指数族的标准形式:

P ( x ∣ η ) = h ( x ) exp ⁡ ( η T T ( x ) − A ( η ) ) P(x|\eta) = h(x) \exp\left(\eta^T T(x) - A(\eta)\right) P(x∣η)=h(x)exp(ηTT(x)−A(η))

这是概率分布的"元素周期表",涵盖了几乎所有常用的分布。

2. 对数配分函数的核心性质:

∇ η A ( η ) = E [ T ( x ) ] (一阶导数 = 期望) ∇ η 2 A ( η ) = Cov [ T ( x ) ] (二阶导数 = 协方差) I ( η ) = ∇ η 2 A ( η ) (Fisher 信息) \begin{aligned} \nabla_\eta A(\eta) &= \mathbb{E}[T(x)] \quad \text{(一阶导数 = 期望)} \\ \nabla^2_\eta A(\eta) &= \text{Cov}[T(x)] \quad \text{(二阶导数 = 协方差)} \\ \mathcal{I}(\eta) &= \nabla^2_\eta A(\eta) \quad \text{(Fisher 信息)} \end{aligned} ∇ηA(η)∇η2A(η)I(η)=E[T(x)](一阶导数 = 期望)=Cov[T(x)](二阶导数 = 协方差)=∇η2A(η)(Fisher 信息)

这些性质使得 MLE 成为凸优化问题,保证了优化的稳定性和唯一性。

3. 最大熵原理:

给定矩约束,指数族分布是唯一最大熵分布:

max ⁡ H [ P ] s.t. E [ T k ( x ) ] = α k ⇒ P ( x ) = exp ⁡ ( ∑ λ k T k ( x ) − A ( λ ) ) \max H[P] \quad \text{s.t.} \quad \mathbb{E}[T_k(x)] = \alpha_k \quad \Rightarrow \quad P(x) = \exp\left(\sum \lambda_k T_k(x) - A(\lambda)\right) maxH[P]s.t.E[Tk(x)]=αk⇒P(x)=exp(∑λkTk(x)−A(λ))

这从信息论角度解释了为什么指数族无处不在:它们是最保守、最无偏的选择。

4. GLM 的统一公式:

所有广义线性模型共享同一个梯度:

∇ w L ( w ) = − ∑ i = 1 N ( y i − μ i ) x i \nabla_w \mathcal{L}(w) = -\sum_{i=1}^N (y_i - \mu_i) x_i ∇wL(w)=−i=1∑N(yi−μi)xi

其中 μ i = ∇ η A ( η i ) ∣ η i = w T x i \mu_i = \nabla_\eta A(\eta_i)|_{\eta_i = w^T x_i} μi=∇ηA(ηi)∣ηi=wTxi。

线性回归、逻辑回归、泊松回归本质相同,只是选择了不同的 A ( η ) A(\eta) A(η)。

5.2 为什么指数族如此重要?

统计学: 充分统计量、MLE 的矩匹配、Fisher 信息
信息论: 最大熵原理
优化: 凸性保证
机器学习: GLM、变分推断的基础 (将在第5章讨论)

指数族不仅仅是一个数学定义,而是:

统计学的基础
信息论的体现
优化的福音
机器学习的支柱

当你遇到一个新的概率模型时,首先问:它是指数族吗? 如果是,你就拥有了这一整套强大的工具。

5.3 关键公式速查表

性质	公式	备注
标准形式	P ( x ∣ η ) = h ( x ) exp ⁡ ( η T T ( x ) − A ( η ) ) P(x \mid \eta) = h(x) \exp(\eta^T T(x) - A(\eta)) P(x∣η)=h(x)exp(ηTT(x)−A(η))	定义
对数配分函数	A ( η ) = log ⁡ ∫ h ( x ) exp ⁡ ( η T T ( x ) ) d x A(\eta) = \log \int h(x) \exp(\eta^T T(x)) \, dx A(η)=log∫h(x)exp(ηTT(x))dx	归一化
一阶导数	∇ η A ( η ) = E [ T ( x ) ] \nabla_\eta A(\eta) = \mathbb{E}[T(x)] ∇ηA(η)=E[T(x)]	期望
二阶导数	∇ η 2 A ( η ) = Cov [ T ( x ) ] \nabla^2_\eta A(\eta) = \text{Cov}[T(x)] ∇η2A(η)=Cov[T(x)]	协方差
Fisher 信息	I ( η ) = ∇ η 2 A ( η ) \mathcal{I}(\eta) = \nabla^2_\eta A(\eta) I(η)=∇η2A(η)	可估计性
MLE 条件	∇ η A ( η ^ ) = T ˉ \nabla_\eta A(\hat{\eta}) = \bar{T} ∇ηA(η^)=Tˉ	矩匹配
GLM 梯度	∇ w L = − ∑ ( y i − μ i ) x i \nabla_w \mathcal{L} = -\sum (y_i - \mu_i) x_i ∇wL=−∑(yi−μi)xi	统一公式
最大熵	P ( x ) = exp ⁡ ( ∑ λ k T k ( x ) − A ( λ ) ) P(x) = \exp(\sum \lambda_k T_k(x) - A(\lambda)) P(x)=exp(∑λkTk(x)−A(λ))	无偏选择
凸性	A ( η ) 是凸函数 A(\eta) \text{ 是凸函数} A(η) 是凸函数	优化保证

参考文献

Bishop, C. M. (2006). Pattern Recognition and Machine Learning. Springer, Chapter 2.
Murphy, K. P. (2022). Probabilistic Machine Learning: An Introduction. MIT Press, Chapter 3.
Wainwright, M. J., & Jordan, M. I. (2008). Graphical Models, Exponential Families, and Variational Inference. Foundations and Trends in Machine Learning, 1(1-2), 1-305.
Jaynes, E. T. (1957). Information Theory and Statistical Mechanics. Physical Review, 106(4), 620-630.
Nelder, J. A., & Wedderburn, R. W. M. (1972). Generalized Linear Models. Journal of the Royal Statistical Society: Series A, 135(3), 370-384.

【机器学习教程】第04章 指数族分布

第04章 指数族分布

前言

目录

引言

1. 指数族分布的定义

1.1 从伯努利分布开始

1.2 高斯分布的改写

1.3 指数族的标准形式

1.4 对数配分函数的定义

1.5 常见分布的指数族形式

2. 指数族分布的性质

2.1 一阶导数:期望

2.2 二阶导数:方差

2.3 Fisher 信息矩阵

2.4 最大似然估计的矩匹配

3. 指数族分布与最大熵

3.1 问题:如何选择概率分布?

3.2 熵与最大熵原理

3.3 推导:最大熵分布是指数族

3.4 例子 1:高斯分布

3.5 例子 2:指数分布

3.6 例子 3:离散均匀分布

4. 指数族分布与广义线性模型 (GLM)

4.1 问题:线性回归与逻辑回归的统一

4.2 GLM 的定义

4.3 核心推导:GLM 的统一梯度公式

4.4 Hessian 矩阵:凸性保证

4.5 例子 1:线性回归 (高斯 GLM)

4.6 例子 2:逻辑回归 (伯努利 GLM)

4.7 例子 3:泊松回归 (泊松 GLM)

4.8 GLM 的几何理解

5. 总结

5.1 主要结论

5.2 为什么指数族如此重要?

5.3 关键公式速查表

参考文献

【机器学习教程】第04章指数族分布

第04章指数族分布