❤️@燃于AC之乐 来自重庆 计算机专业的一枚大学生
✨专注 C/C++ Linux 数据结构 算法竞赛 AI
🏞️志同道合的人会看见同一片风景!
👇点击进入作者专栏:
🌟《算法画解》算法相关题目点击即可进入实操🌟
感兴趣的可以先收藏起来,请多多支持,还有大家有相关问题都可以给我留言咨询,希望希望共同交流心得,一起进步,你我陪伴,学习路上不孤单!
文章目录
前言
这些题目摘录于洛谷,好题,典型的题,考察各类算法运用,可用于蓝桥杯及各类算法比赛备战,算法题目练习,提高算法能力,补充知识,提升思维。
锻炼解题思路,从学会算法模板后,会分析,用到具体的题目上。
对应题目点链接即可做。
本期涉及算法:二进制枚举,模拟,贪心,贪心 + 并查集 + kruskal算法,双指针,区间dp(动态规划)。
题目清单
1.PERKET
题目: P2036 [COCI 2008/2009 #2] PERKET

解法:二进制枚举
从 n 种食材中选择若干种(至少一种),使得 酸度乘积 与 苦度之和 的绝对差最小。
核心思路
- 使用 二进制枚举 遍历所有非空选择方案
- 二进制位为 1 表示选择对应食材
- 计算每种方案的酸度乘积和苦度之和
- 更新最小绝对差值
关键代码解释
st 从 1 到 (1<<n)-1:枚举所有非空子集(至少选一种)
(st>>i)&1`:检查第 i 种食材是否被选中
x 累乘酸度,y` 累加苦度
更新最小差值 ret = min(ret, abs(x-y))
代码:
cpp
#include <iostream>
#include <cmath>
using namespace std;
const int N = 15;
typedef long long LL;
LL n, s[N], b[N];
int main()
{
cin >> n;
for(int i = 0; i < n; i++) cin >> s[i] >> b[i];
LL ret = 1e19;
for(int st = 1; st < (1 << n); st++)
{
LL x = 1, y = 0;
for(int i = 0; i < n; i++)
{
if((st >> i) & 1)
{
x *= s[i];
y += b[i];
}
}
ret = min(ret, abs(x - y));
}
cout << ret << endl;
return 0;
}2.生活大爆炸版石头剪刀布
题目: P1328 [NOIP 2014 提高组] 生活大爆炸版石头剪刀布
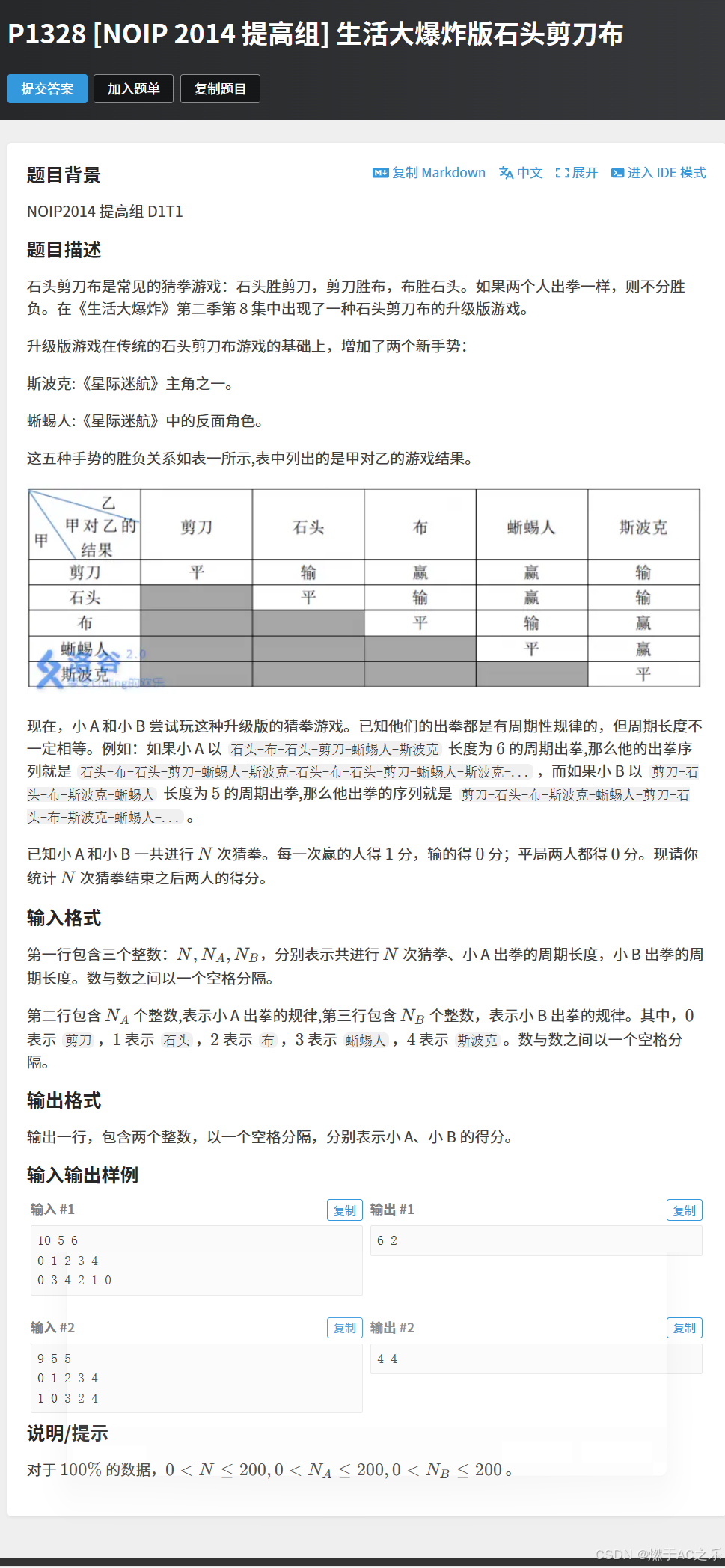
解法:模拟
这道题用1,0,-1来分别表示赢,平局,输,用一个c[5] [5] 的二维数组来表示所有情况。 对于两个都有周期情况,取模周期即可。
x = i % n1, y = i % n2,c[a[x]] [b[y]]。
代码:
cpp
#include <iostream>
using namespace std;
const int N = 210;
int n, n1, n2;
int a[N], b[N];
int c[5][5] = {0, -1, 1, 1, -1,
1, 0, -1, 1, -1,
-1, 1, 0, -1, 1,
-1, -1, 1, 0, 1,
1, 1, -1, -1, 0};
int main()
{
cin >> n >> n1 >> n2;
for(int i = 0; i < n1; i++) cin >> a[i];
for(int i = 0; i < n2; i++) cin >> b[i];
int A = 0, B = 0;
for(int i = 0; i < n; i++)
{
int x = i % n1, y = i % n2;
int t = c[a[x]][b[y]];
if(t > 0) A++;
else if(t < 0) B++;
}
cout << A << " " << B << endl;
return 0;
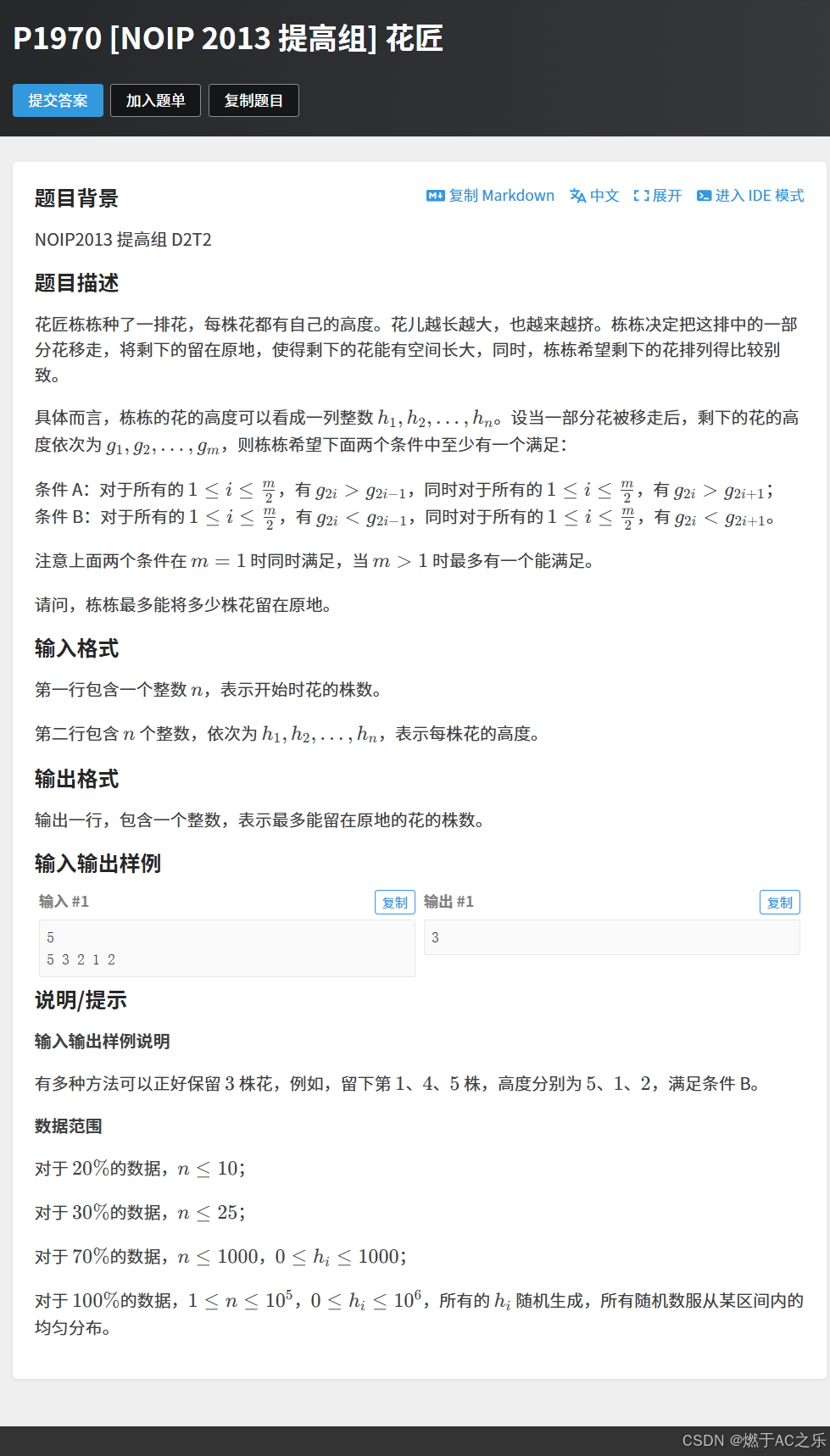
}3.花匠
解法:贪心
这道题目是求摆动序列的经典问题。
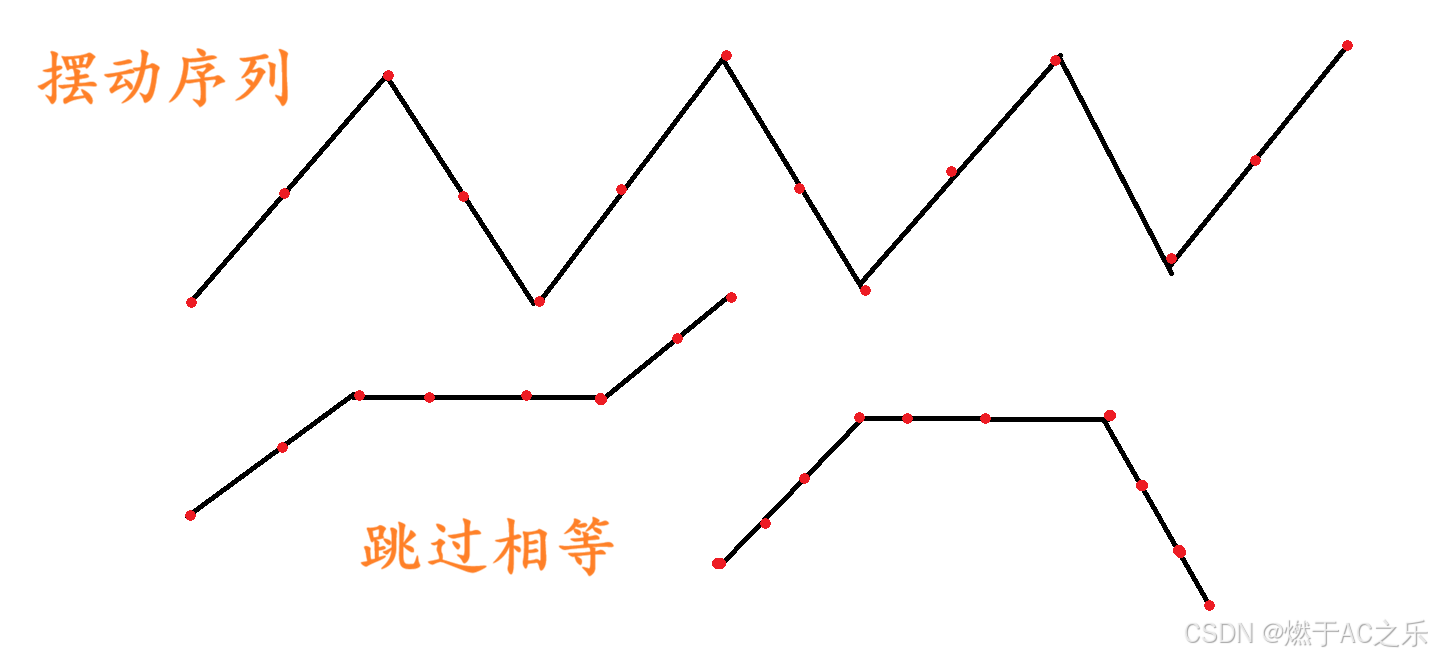
对于某⼀个位置i来说:
如果接下来呈现上升趋势的话,我们让其上升到波峰的位置;
如果接下来呈现下降趋势的话,我们让其下降到波谷的位置。
因此,如果把整个数组放在「折线图」中,我们统计出所有的波峰以及波谷的个数即可。
用一个prev数组标记,初始为0,如果前一个是上升过来的就为1,下降就为-1,起点为0,对于点i就是求d = h[i + 1] - h[i] 是>0 还是 < 0,于prev比较,更新出极大值,极小值,cnt++。 注意:1.可能出现一样高的点 ,就要特判, d==0时跳过 。 2.因为最后一个点 没法统计,就在结果cnt+1。
代码:
cpp
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int n;
int h[N];
int main()
{
cin >> n;
for(int i = 1; i <= n; i++) cin >> h[i];
int prev = 0, cnt = 0;
for(int i = 1; i < n; i++)
{
int d = h[i + 1] - h[i];
if(d == 0) continue;
d = (d > 0 ? 1 : -1);
if(d != prev) cnt++;
prev = d;
}
cout << cnt + 1 << endl;
return 0;
}4.营救
题目: P1396 营救

解法:贪心 + 并查集 + kruskal算法
找一条从 s 到 t 的路径,使得路径上最大的边权最小。
这里看到最大值最小想到用二分算法,然后有连通性(起点到终点)的判断,考虑到用并查集。
但是这里可以贪心地从小到大来选,排序即可,不用二分去找,时间复杂度更优。
思路分析
采用Kruskal算法变体:
- 将所有边按拥挤度(边权)从小到大排序
- 依次加入边,同时用并查集维护连通性
- 当 s 和 t 第一次连通时,最后加入的边权即为答案
算法正确性
按边权从小到大加边,第一次使 s 和 t 连通时:
当前边 w 是路径上最大边权(因为是按序加入)
任何更小的边权都无法使 s 和 t 连通
因此 w 是最小的最大拥挤度
O(m log m),m≤2×10⁴
代码:
cpp
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e4 + 10, M = 2e4 + 10;
int n, m, s, t;
struct node
{
int u, v, w;
}e[M];
bool cmp(node& x, node& y)
{
return x.w < y.w;
}
int fa[N];
int find(int x)
{
return x == fa[x] ? x : fa[x] = find(fa[x]);
}
void un(int x, int y)
{
fa[find(x)] = find(y);
}
int main()
{
cin >> n >> m >> s >> t;
for(int i = 1; i <= m; i++) cin >> e[i].u >> e[i].v >> e[i].w;
sort(e + 1, e + 1 + m, cmp);
//初始化
for(int i = 1; i <= n; i++) fa[i] = i;
int ret = e[m].w;
for(int i = 1; i <= m; i++)
{
int u = e[i].u, v = e[i].v, w = e[i].w;
un(u, v);
ret = w;
if(find(s) == find(t)) break;
}
cout << ret << endl;
return 0;
}5.School Photo
题目: P10710 [NOISG 2024 Prelim] School Photo
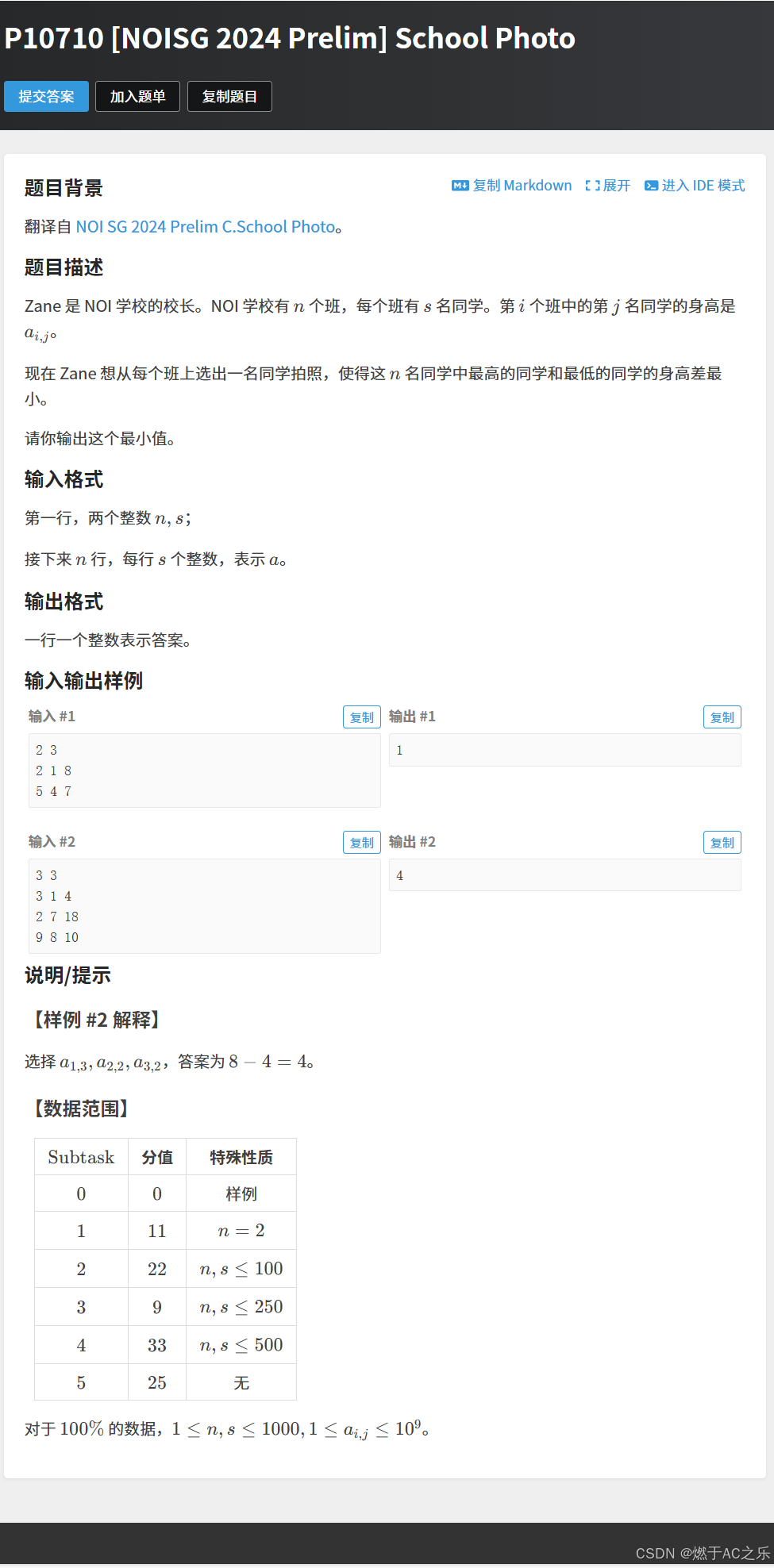
解法:双指针
问题核心
从 n 个班各选一人,使最高与最矮身高差最小。
这道题:从每个班选人,会很自然的想到分组背包解法,但是时间、空间复杂度较大,且状态转移方程不好写。
算法思路
-
合并排序:将所有学生按身高排序,记录所属班级
-
滑动窗口:
右指针 r 扩展,统计覆盖的班级种类数
当覆盖全部 n 个班时:
更新答案:
ret = min(ret, 最大身高 - 最小身高)左指针 l 右移,直到不再覆盖全部班级
-
本质:寻找包含所有班级的最短连续子序列
复杂度
O(m log m),m = n × s ≤ 10⁶。
关键点
用 cnt[] 统计窗口内各班级人数,kind 记录覆盖的班级数,确保每班至少一人。
代码:
cpp
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010, M = N * N;
int n, m, s;
struct node
{
int h, id;
}a[M];
int cnt[N];
bool cmp(node& x, node& y)
{
return x.h < y.h;
}
int main()
{
cin >> n >> s;
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= s; j++)
{
m++;
cin >> a[m].h;
a[m].id = i;
}
}
sort(a + 1 , a + 1 + m, cmp);
int ret = 1e9;
for(int l = 1, r = 1, kind = 0; r <= m; r++)
{
//a[r]
cnt[a[r].id]++;
//0 -> 1
if(cnt[a[r].id] == 1) kind++;
while(kind == n)
{
ret = min(ret, a[r].h - a[l].h);
cnt[a[l].id]--;
//1 -> 0
if(cnt[a[l].id] == 0) kind--;
l++;
}
}
cout << ret << endl;
return 0;
}6.Zuma
题目: CF607B Zuma

解法:区间dp(动态规划)
看到这里不断对一个区间做处理(消除) ,又是回文 ,求最短的时间 ,想到用区间dp来解决。
1.状态表示:
f[i] [j]表示:将区间 [i, j] 完全消除,所需最短时间。 结果: f[1] [n]。
2.状态转移方程:
1.枚举区间分割点 k(i <= k < j), 整个区间被分为 [i, k] 和 [k + 1, j], f[i, k] + f[k + 1, j]。
2.因为是回文处理且将端点包括在内一起消除,那么如果a[i] == a[j], 就还要再加一步判断min(f[i] [j], f[i + 1] [j - 1])。
3.初始化:
这里求最小值,且为了不影响后续更新:
先将全部初始化为正无穷,然后再分别初始化,len = 1, len = 2;
len = 1, f[i] [i] = 1;
len =2, a[i] = a[i + 1] , f[i] [i + 1] = 1, a[i] != a[i + 1], f[i] [i + 1] = 2。
4.填表顺序:
先枚举区间长度,再枚举左右端点。
代码:
cpp
#include <iostream>
#include <cstring>
using namespace std;
const int N = 510;
int n;
int a[N];
int f[N][N];
int main()
{
cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
//初始化
memset(f, 0x3f, sizeof f);
for(int i = 1; i <= n; i++) f[i][i] = 1; //len = 1
for(int i = 1; i + 1 <= n; i++) //len = 2
{
int j = i + 1;
if(a[i] == a[j]) f[i][j] = 1;
else f[i][j] = 2;
}
for(int len = 3; len <= n; len++)
{
for(int i = 1; i + len - 1 <= n; i++)
{
int j = i + len - 1;
for(int k = i; k < j; k++)
{
//[i, k] [k + 1, j]
f[i][j] = min(f[i][j], f[i][k] + f[k + 1][j]);
}
if(a[i] == a[j]) f[i][j] = min(f[i][j], f[i + 1][j - 1]); //回文拿走包括端点
}
}
cout << f[1][n] << endl;
return 0;
}

加油!志同道合的人会看到同一片风景。
看到这里请点个赞 ,关注 ,如果觉得有用就收藏一下吧。后续还会持续更新的。 创作不易,还请多多支持!