目录
[4.只出现一次的数字 II](#4.只出现一次的数字 II)
[5. 消失的两个数字](#5. 消失的两个数字)
前言
本篇博客是对位运算算法一部分经典题目的整理与每道题很详细的思考与题解过程,相信大家看完能对位运算类型的相关问题有一定的理解和掌握
常见位运算总结
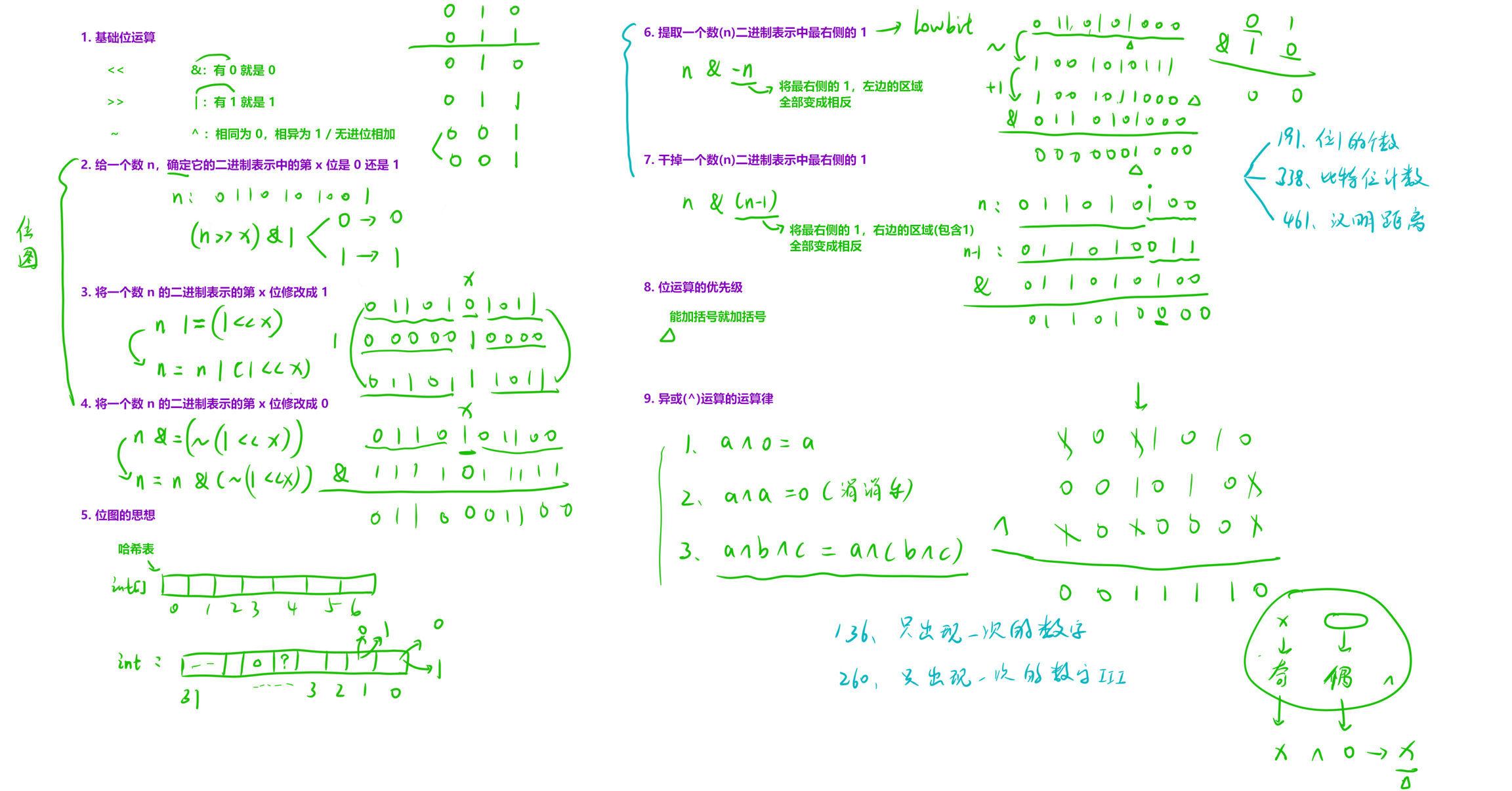
<<是 左移运算符>>是 右移运算符
1.判定字符是否唯一

算法原理
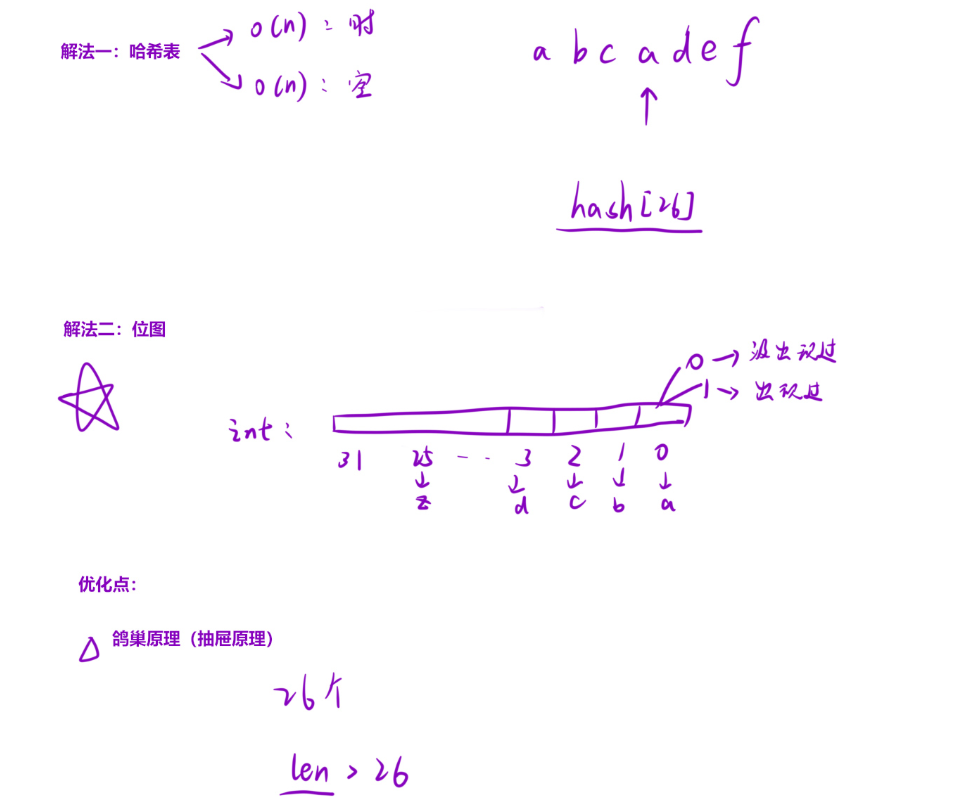
- 解法一就是通过把数组中字符在对应哈希表的位置中进行计数,如果哈希表该位置字符存的值大于了1就返回false,循环完即返回true(这里就创建一个26大小的数组充当哈希表即可)
解题代码:c++
cpp
class Solution {
public:
bool isUnique(string astr)
{
//只有小写字母,那么如果这个字符串长度超过26了
//就说明一定会有重复的字符,此时直接返回false作优化------ 鸽巢原理
if(astr.size()>26) return false;
//利用位图来解决
int bitMap=0; //利用一个整型变量当作位图(32位>26够用)
for(auto ch:astr)
{
int i=ch-'a';//找到该字符对应位图的下标
//先判断该字符是否已经存在于位图中
if((bitMap>>i)&1) //查看第i位是否为1操作
{
//为1说明已经存在,该字符不是唯一的
return false;
}
//到这说明不存在位图中,将该字符加入即可
bitMap|=1<<i;
}
//出来就说明该字符串中所有字符全都不同
return true;
}
};2.丢失的数字

算法原理
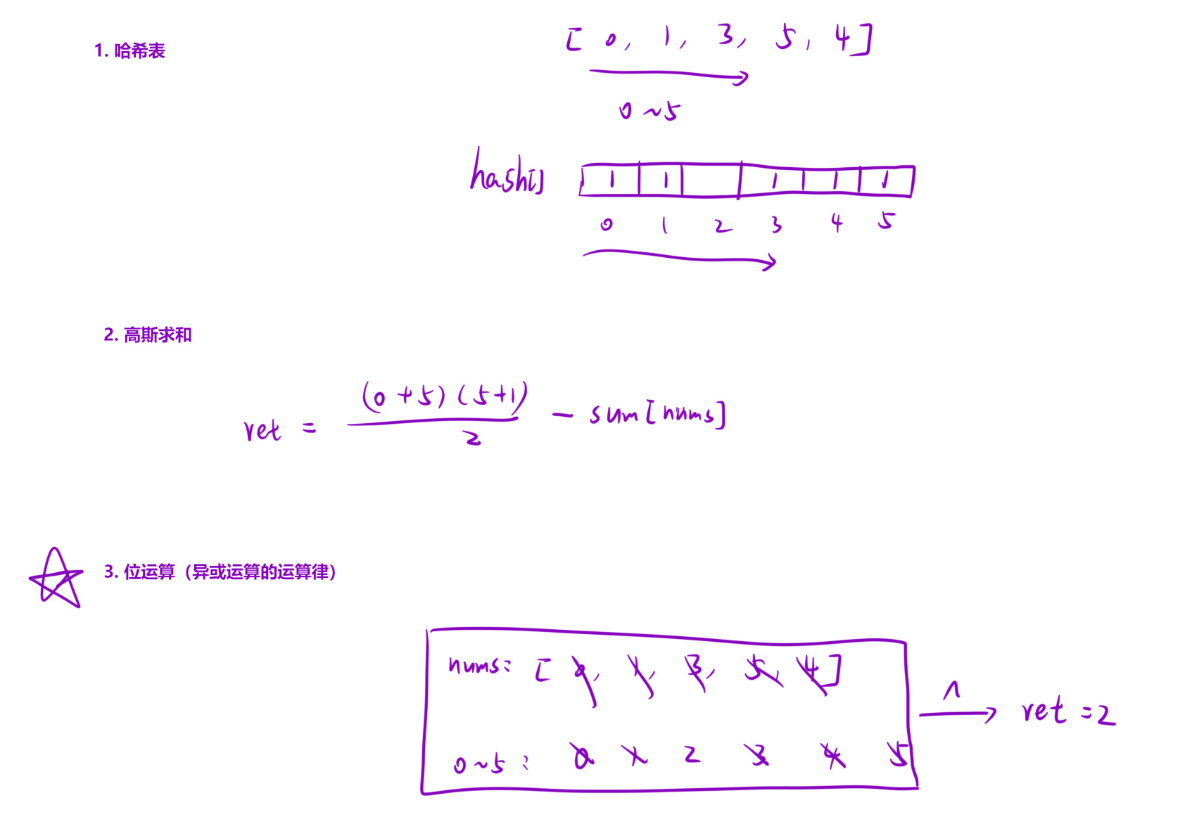
- 高斯求和:求一个连线递增数组中的和,那么就是首项加末项的和乘以项数再除以2;那么这个用来求完整数组的和,我们再遍历求出缺失数组的和,两者相减就是缺失de
解题代码:c++
cpp
class Solution {
public:
int missingNumber(vector<int>& nums)
{
//让这个数组与完整的数组相异或,结果就是那个少了的数
//由于题目性质,这个nums数组是一定会少一个元素
//那么这个完整数组最大的元素就是nums的长度+1
int n=nums.size();
int ans=0,i=0;
for(;i<n;i++)
{
ans^=nums[i];
ans^=i;
}
ans^=i;//最后再把完整的数组最后一个元素异或上
return ans;
}
};3.两整数之和

算法原理
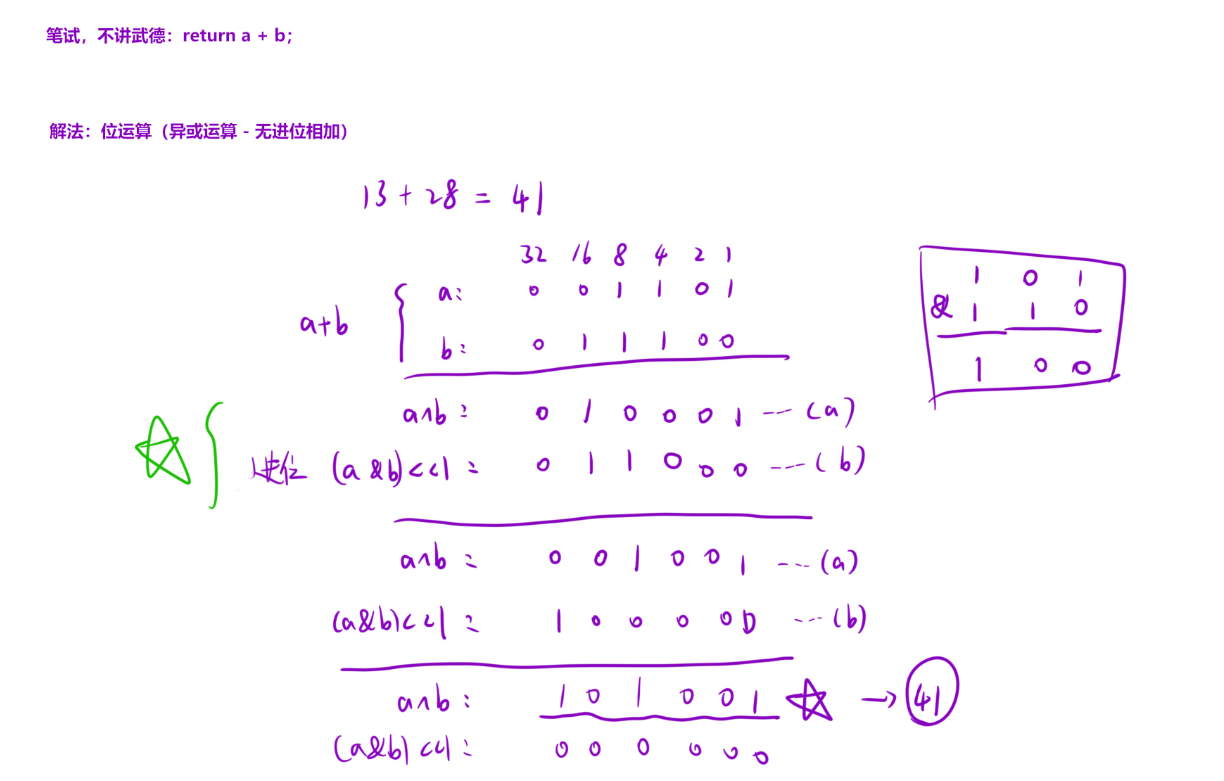
解题代码:c++
cpp
class Solution {
public:
int getSum(int a, int b)
{
while(b!=0)
{
int x=a^b;//先算出无进位相加的结果
unsigned int carry=(unsigned int)(a&b)<<1;//算出进位
a=x;
b=carry;
}
return a;
}
};4.只出现一次的数字 II
算法原理
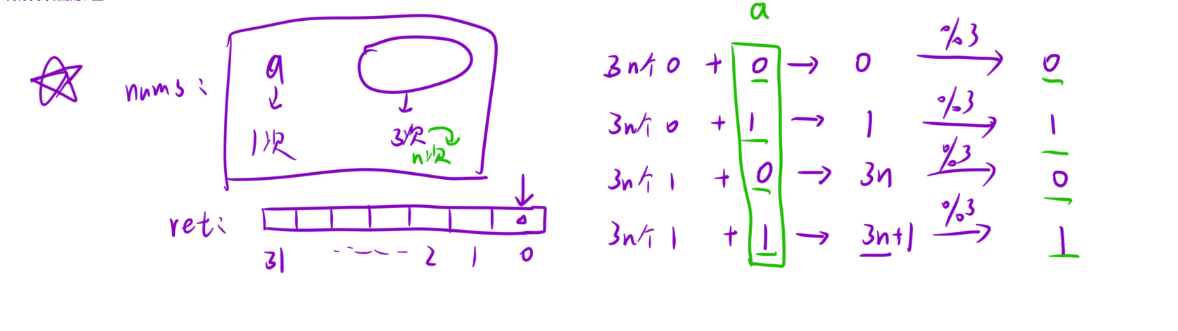
这里就是把nums中所有数的某一位相加起来%上3,此时的结果和我们的唯一数该位的值是一致的,将ret结果数组中的对应位修改成该值,那么我们依次这里操作完这个ret数组就是我们结果的对应的二进制了
拓展:如果其他数是出现n次的,那么把模3改成模n即可
解题代码:c++
cpp
class Solution {
public:
int singleNumber(vector<int>& nums)
{
int ret=0; //用整型变量当作结果二进制数组转换整型形式
for(int i=0;i<32;i++) //依次去修改ret中每一位
{
int sum=0; //统计所有元素第i位的和
for(auto x:nums) //遍历nums中的每一个数
{
if(((x>>i)&1)==1)
sum++;
}
sum%=3;
if(sum==1) ret|=1<<i; //将第i位修改为1
}
return ret;
}
};5. 消失的两个数字

算法原理
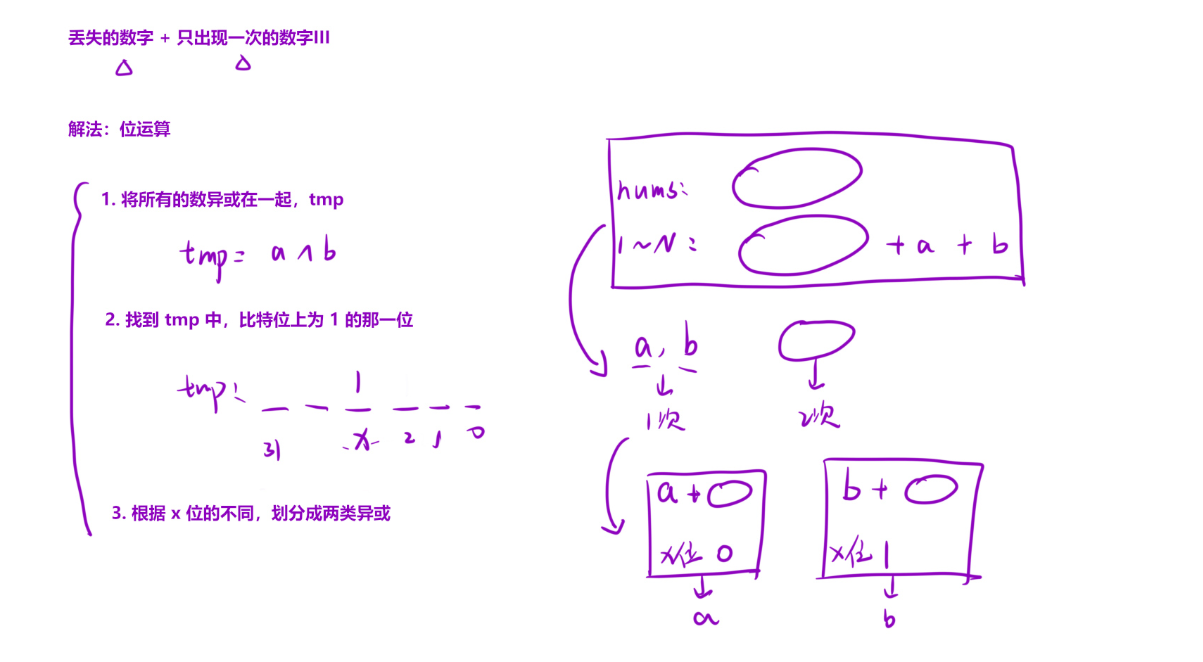
解题代码:c++
cpp
class Solution {
public:
vector<int> missingTwo(vector<int>& nums)
{
//其实就是丢失的数字+只出现一次的数字III的结合版
//那么我们的解法也结合一下即可,就先原数组和完整数组异或
//然后lowbit找到右侧第一个1进行分组再异或求得两个消失的数
//其实也就是看看完整数组和原数组和一起之后只出现一次的数
//第一步
int tmp=0;
for(int i=0;i<nums.size();i++)
{
tmp^=nums[i];
}
//再异或上完整数组
for(int i=1;i<=nums.size()+2;i++) tmp^=i;
//第二步
int lowbit=tmp&-tmp;
//分组
int num1=0,num2=0;
for(int i=0;i<nums.size();i++)
{
if(nums[i]&lowbit!=0) num1^=nums[i];
else num2^=nums[i];
}
for(int i=1;i<=nums.size()+2;i++)
{
if(i&lowbit) num1^=i;
else num2^=i;
}
return {num1,num2};
}
};