1. 相关概念
1.1 计数原理
分类相加,分步相乘。
【加法原理】
如果完成⼀个事件有 类⽅法,其中 表⽰第 类⽅法的⽅法数。那么完成这件事⼀共有 a ∑ i =1
种⽅法。
【乘法原理】
如果完成⼀个事件有 个步骤,其中 表⽰第 个步骤的⽅法数。那么完成这件事⼀共有
种⽅法。
例如:书架上有不同的数学书 3 本,不同的物理书 4 本,不同的化学书 5 本。
- 从中任取⼀本,有多少种不同的取法?
- 从中每种各取⼀本,有多少种不同的取法?
解: - 由加法原理,共有 3 + 4 + 5 = 12 种不同的取法。
- 由乘法原理,共有 3 × 4 × 5 = 60 种不同的取法。
1.2 排列组合
排列组合是组合数学中的基础。
排列组合的中⼼问题是研究给定要求的排列和组合可能出现的情况总数.


1.3 ⼆项式定理

2. 求组合数
基本上所有的组合数学问题,最终都会变成求出若⼲个组合数或者排列数。下⾯介绍 种常⽤的求组 合数的⽅法,做题的时候根据数据范围和题⽬要求,灵活使⽤。⽆论选择哪种⽅式,注意以下两点:
- 计算的结果⼀般都很⼤,因此求解的时候基本都需要取模,此时就要⽤到之前学过的乘法逆元的知 识;
- 选择不同的公式,计算结果的时间复杂度不同,因此要选择合适的公式。
【⽅式⼀:循环】
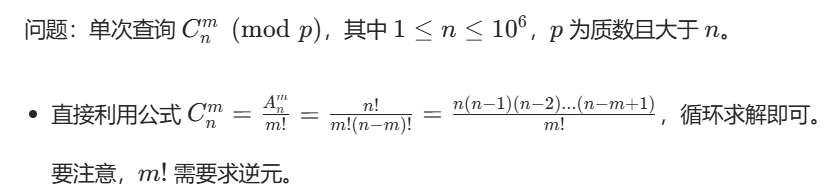
扩展
• 如果多次查询,但是 m 的值很⼩,也可以利⽤公式直接求解。
代码实现:
cpp
#include <iostream>
using namespace std;
// 先定义 LL 类型(避免代码报错,通常竞赛中 typedef long long LL;)
typedef long long LL;
/**
* @brief 快速幂算法:计算 (a^b) mod p 的结果
* @param a 底数
* @param b 指数(非负整数)
* @param p 模数(质数,本题中用于组合数取模)
* @return LL (a^b) % p 的结果
* 核心思想:二进制分解指数,将幂运算的时间复杂度从 O(b) 降到 O(logb)
*/
LL qpow(LL a, LL b, LL p)
{
LL ret = 1; // 初始化结果为 1(乘法单位元)
while(b) // 当指数 b > 0 时循环
{
// 如果 b 的二进制最后一位是 1(即 b 是奇数),将当前 a 乘到结果中并取模
if(b & 1) ret = ret * a % p;
a = a * a % p; // 底数平方,对应指数二进制左移一位
b >>= 1; // 指数右移一位(等价于 b = b / 2),处理下一位
}
return ret; // 返回最终的 (a^b) mod p
}
/**
* @brief 计算组合数 C(n, m) mod p 的结果(p 是质数且 p > n)
* @param n 总元素数
* @param m 选取的元素数
* @param p 模数(质数,且 p > n,保证阶乘无因子 p,逆元存在)
* @return LL C(n, m) % p 的结果
* 公式:C(n,m) = n!/(m!*(n-m)!) = [n*(n-1)*...*(n-m+1)] / (m!)
* 取模下除法转乘法:除以 m! 等价于乘以 m! 的模 p 逆元(费马小定理)
*/
LL C(int n, int m, int p)
{
if(n < m) return 0; // 特殊情况:选取数 > 总数,组合数为 0
LL up = 1, down = 1; // up:分子(n*(n-1)*...*(n-m+1));down:分母(m!)
// 第一步:计算分子 up = (n-m+1) * (n-m+2) * ... * n mod p
// 等价于 n!/(n-m)! mod p,直接累乘避免计算大数阶乘
for(LL i = n - m + 1; i <= n; i++)
up = up * i % p; // 每一步取模,防止溢出
// 第二步:计算分母 down = m! mod p
for(LL i = 2; i <= m; i++)
down = down * i % p; // 从 2 开始累乘(1的阶乘不影响结果)
// 第三步:计算 C(n,m) mod p = (up * inv(down)) mod p
// 费马小定理:若 p 是质数,inv(x) = x^(p-2) mod p(x 与 p 互质)
// qpow(down, p-2, p) 即求 down 的模 p 逆元
return up * qpow(down, p - 2, p) % p;
}时间复杂度:
• 查询: O ( m )
【⽅式⼆:杨辉三⻆】

代码实现
cpp
#include <iostream>
using namespace std;
typedef long long LL; // 定义LL为long long,避免溢出,统一数据类型
const int N = 2010; // 数组最大维度,适配题目中n≤2000的限制(多开10位防越界)
int n, p; // 全局变量:n是组合数的最大上界(C(n,m)中的n),p是模数
LL f[N][N]; // 二维数组f[i][j]存储C(i,j) mod p的结果(杨辉三角表)
/**
* @brief 预处理杨辉三角,打表所有C(i,j) mod p的值(0≤j≤i≤n)
* 核心原理:组合数递推公式 C(i,j) = C(i-1,j) + C(i-1,j-1)
* 边界条件:C(i,0) = 1(从i个元素选0个,只有1种选法)
* 适用场景:多次查询C(n,m) mod p,且n≤2000、查询次数极多(如1e6次)
*/
void get_c()
{
// 遍历杨辉三角的每一行(对应组合数的上标i)
for(int i = 0; i <= n; i++)
{
// 边界条件1:C(i,0) = 1(选0个元素的组合数恒为1),且取模p
f[i][0] = 1;
// 遍历当前行的每一列(对应组合数的下标j),j最大为i(C(i,j)中j≤i)
for(int j = 1; j <= i; j++)
{
// 递推公式:C(i,j) = (C(i-1,j) + C(i-1,j-1)) mod p
// 解释:
// - C(i-1,j):不选第i个元素,从i-1个中选j个的组合数
// - C(i-1,j-1):选第i个元素,从i-1个中选j-1个的组合数
// 取模p:防止数值溢出,且满足题目"模p"的要求
f[i][j] = (f[i - 1][j] + f[i - 1][j - 1]) % p;
}
}
}
int main()
{
// 注意:实际使用时需先输入n和p,再调用get_c()
// 示例:输入n=5,p=7,预处理后f[5][2]就是C(5,2) mod7=10 mod7=3
// cin >> n >> p;
get_c(); // 调用函数预处理组合数表
// 预处理完成后,查询C(a,b) mod p只需直接取f[a][b](需保证b≤a≤n)
// 示例:查询C(5,2) mod7,输出f[5][2] → 3
// cout << f[5][2] << endl;
return 0;
}时间复杂度:
• 打表: O ( n 2 )
• 查询: O (1)
【⽅式三:阶乘以及阶乘逆元表 + 公式】


代码实现
cpp
#include <iostream>
using namespace std;
typedef long long LL; // 定义LL为long long,防止阶乘/逆元计算溢出
const int N = 1e6 + 10; // 数组最大维度,适配n≤1e6的限制(多开10位防越界)
int n, p; // 全局变量:n是阶乘预处理的最大上界,p是模数(质数且p>n)
LL f[N]; // f[i] = i! mod p(存储i的阶乘模p的结果)
LL g[N]; // g[i] = (i!)^{-1} mod p(存储i!的模p逆元)
/**
* @brief 快速幂算法:计算 (a^b) mod p 的结果(费马小定理求逆元的核心)
* @param a 底数(此处用于传入阶乘值f[n])
* @param b 指数(此处常用p-2,对应费马小定理的逆元公式)
* @param p 模数(质数)
* @return LL (a^b) % p 的结果
* 时间复杂度:O(logb),高效处理大指数运算
*/
LL qpow(LL a, LL b, LL p)
{
LL ret = 1; // 初始化结果为1(乘法单位元)
while(b) // 指数b>0时循环(二进制分解指数)
{
// 如果b的二进制最后一位是1(b为奇数),将当前a乘到结果中并取模
if(b & 1) ret = ret * a % p;
a = a * a % p; // 底数平方,对应指数二进制左移一位
b >>= 1; // 指数右移一位(等价于b = b/2),处理下一位
}
return ret; // 返回最终的(a^b) mod p
}
/**
* @brief 预处理阶乘数组f和阶乘逆元数组g
* 核心逻辑:
* 1. 阶乘f[i]:递推 f[i] = f[i-1] * i % p(从左到右)
* 2. 阶乘逆元g[i]:先求g[n] = (n!)^{-1} mod p(快速幂),再递推 g[i] = (i+1)*g[i+1] % p(从右到左)
*/
void init()
{
f[0] = 1; // 边界条件:0! = 1(阶乘的定义)
// 第一步:预处理阶乘数组f(从1到n)
for(int i = 1; i <= n; i++)
{
// f[i] = i! = (i-1)! * i → 取模p防止溢出
f[i] = f[i - 1] * i % p;
}
// 第二步:求最大阶乘的逆元g[n] = (n!)^{-1} mod p(费马小定理)
// 费马小定理:若p是质数,(n!)^{p-2} ≡ (n!)^{-1} mod p
g[n] = qpow(f[n], p - 2, p);
// 第三步:递推求所有阶乘的逆元(从n-1到0,从右到左)
// 递推公式:g[i] = (i+1) * g[i+1] % p
// 原理:(i!)^{-1} = (i+1) * (i+1)!^{-1} → 因为 (i+1)! = (i+1)*i!
for(int i = n - 1; i >= 0; i--)
{
g[i] = (i + 1) * g[i + 1] % p;
}
}
/**
* @brief 计算组合数 C(n,m) mod p
* 公式:C(n,m) = n!/(m!*(n-m)!) mod p = f[n] * g[m] * g[n-m] mod p
* @param n 总元素数
* @param m 选取的元素数
* @return LL C(n,m) mod p 的结果(n<m时返回0)
*/
LL C(int n, int m)
{
if(n < m) return 0; // 特殊情况:选取数>总数,组合数为0
// 分步取模:避免一次性乘法溢出,保证每一步结果在p范围内
return f[n] * g[n - m] % p * g[m] % p;
}时间复杂度:
• 打表: O ( n )
• 查询: O (1)
【⽅式四:卢卡斯定理】

代码实现
cpp
#include <iostream>
using namespace std;
typedef long long LL; // 定义LL为long long,适配n≤1e18的超大数
const int N = 1e5 + 10; // 数组维度适配p≤1e5的限制(p是质数且≤1e5)
LL n, m, p; // 全局变量:n=C(n,m)的上标,m=下标,p=模数(质数≤1e5)
LL f[N], g[N]; // f[i]=i! mod p;g[i]=(i!)^{-1} mod p(仅预处理到p-1)
/**
* @brief 快速幂:计算(a^b) mod p,用于求逆元(费马小定理)
* @param a 底数(此处传入阶乘值f[n])
* @param b 指数(此处常用p-2,对应逆元公式)
* @param p 模数(质数)
* @return LL (a^b) mod p的结果,时间复杂度O(logb)
*/
LL qpow(LL a, LL b, LL p)
{
LL ret = 1; // 初始化结果为1(乘法单位元)
while(b) // 二进制分解指数b,直到b=0
{
// b&1:判断b的二进制最后一位是否为1(即b是否为奇数)
if(b & 1) ret = ret * a % p; // 若为1,将当前a乘到结果中并取模
a = a * a % p; // 底数平方,对应指数左移一位
b >>= 1; // 指数右移一位(等价于b = b/2)
}
return ret; // 返回最终的(a^b) mod p
}
/**
* @brief 预处理:计算1~p-1的阶乘f[]和阶乘逆元g[](仅预处理到p-1,因为Lucas中只用到n%p/m%p)
* 核心:p≤1e5,预处理代价极低(O(p)),且n%p/m%p一定≤p-1
*/
void init()
{
int max_fact = p - 1; // 阶乘只需预处理到p-1(因为模p下,≥p的数模p后≤p-1)
f[0] = 1; // 边界条件:0! = 1
// 第一步:递推计算阶乘f[i] = i! mod p(1≤i≤p-1)
for(int i = 1; i <= max_fact; i++)
{
f[i] = f[i - 1] * i % p; // f[i] = (i-1)! * i mod p
}
// 第二步:求最大阶乘的逆元g[p-1] = ((p-1)!)^{-1} mod p(费马小定理)
g[max_fact] = qpow(f[max_fact], p - 2, p);
// 第三步:逆推所有阶乘的逆元g[i] = (i+1)*g[i+1] mod p(从p-2到0)
for(int i = max_fact - 1; i >= 0; i--)
{
g[i] = ((i + 1) * g[i + 1]) % p; // 递推公式,保证每一步取模
}
}
/**
* @brief 计算小范围组合数C(n,m) mod p(n,m ≤ p-1,且p是质数)
* 公式:C(n,m) = n!/(m!*(n-m)!) mod p = f[n] * g[m] * g[n-m] mod p
* @param n 上标(≤p-1)
* @param m 下标(≤p-1)
* @param p 模数(质数)
* @return LL C(n,m) mod p的结果(n<m时返回0)
*/
LL C(int n, int m, LL p)
{
if(n < m) return 0; // 特殊情况:选的数比总数多,组合数为0
// 分步取模:避免一次性乘法溢出,保证结果在p范围内
return f[n] * g[m] % p * g[n - m] % p;
}
/**
* @brief 卢卡斯定理递归求解大组合数C(n,m) mod p(n≤1e18,m≤1e18,p≤1e5且为质数)
* 核心公式:C(n,m) ≡ C(n/p, m/p) * C(n%p, m%p) (mod p)
* 递归边界:m=0时,C(n,0)=1(从n个选0个,只有1种选法)
* @param n 超大上标(≤1e18)
* @param m 超大下标(≤1e18)
* @param p 模数(质数≤1e5)
* @return LL C(n,m) mod p的结果
*/
LL lucas(LL n, LL m, LL p)
{
if(m == 0) return 1; // 递归边界:C(n,0)=1
// 递归分解:
// 1. lucas(n/p, m/p, p):处理高位部分(n/p和m/p是整除结果)
// 2. C(n%p, m%p, p):处理低位部分(n%p/m%p≤p-1,用预处理的f/g数组计算)
// 3. 两部分相乘后取模p,得到当前层结果
return lucas(n / p, m / p, p) * C(n % p, m % p, p) % p;
}时间复杂度: O ( p + log p n )
2.1 组合数问题
题⽬来源: 洛⾕
题⽬链接: P2822 [NOIP2016 提⾼组] 组合数问题
难度系数: ★★
题目背景
NOIP2016 提高组 D2T1
题目描述
组合数 (mn) 表示的是从 n 个物品中选出 m 个物品的方案数。举个例子,从 (1,2,3) 三个物品中选择两个物品可以有 (1,2),(1,3),(2,3) 这三种选择方法。根据组合数的定义,我们可以给出计算组合数 (mn) 的一般公式:
(mn)=m!(n−m)!n!
其中 n!=1×2×⋯×n;特别地,定义 0!=1。
小葱想知道如果给定 n,m 和 k,对于所有的 0≤i≤n,0≤j≤min(i,m) 有多少对 (i,j) 满足 k∣(ji)。
输入格式
第一行有两个整数 t,k,其中 t 代表该测试点总共有多少组测试数据,k 的意义见问题描述。
接下来 t 行每行两个整数 n,m,其中 n,m 的意义见问题描述。
输出格式
共 t 行,每行一个整数代表所有的 0≤i≤n,0≤j≤min(i,m) 中有多少对 (i,j) 满足 k∣(ji)。
输入输出样例
输入 #1复制
1 2
3 3输出 #1复制
1输入 #2复制
2 5
4 5
6 7输出 #2复制
0
7说明/提示
【样例1说明】
在所有可能的情况中,只有 (12)=2 一种情况是 2 的倍数。
【子任务】
| 测试点 | n | m | k | t |
|---|---|---|---|---|
| 1 | ≤3 | ≤3 | =2 | =1 |
| 2 | ≤3 | ≤3 | =3 | ≤104 |
| 3 | ≤7 | ≤7 | =4 | =1 |
| 4 | ≤7 | ≤7 | =5 | ≤104 |
| 5 | ≤10 | ≤10 | =6 | =1 |
| 6 | ≤10 | ≤10 | =7 | ≤104 |
| 7 | ≤20 | ≤100 | =8 | =1 |
| 8 | ≤20 | ≤100 | =9 | ≤104 |
| 9 | ≤25 | ≤2000 | =10 | =1 |
| 10 | ≤25 | ≤2000 | =11 | ≤104 |
| 11 | ≤60 | ≤20 | =12 | =1 |
| 12 | ≤60 | ≤20 | =13 | ≤104 |
| 13 | ≤100 | ≤25 | =14 | =1 |
| 14 | ≤100 | ≤25 | =15 | ≤104 |
| 15 | ≤100 | ≤60 | =16 | =1 |
| 16 | ≤100 | ≤60 | =17 | ≤104 |
| 17 | ≤2000 | ≤100 | =18 | =1 |
| 18 | ≤2000 | ≤100 | =19 | ≤104 |
| 19 | ≤2000 | ≤2000 | =20 | =1 |
| 20 | ≤2000 | ≤2000 | =21 | ≤104 |
- 对于全部的测试点,保证 0≤n,m≤2×103,1≤t≤104。
【解法】
• 打表组合数模 k 的值。
• 维护出组合数表格的前缀和,其中⾮零位置的值为 0,零位置的值为 1。
【参考代码】
cpp
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 2e3 + 10; // 数组维度,适配i,j≤2000的范围(题目隐含数据范围)
int n, m, k;
int f[N][N]; // f[i][j] = C(i,j) mod k(存储组合数模k的结果)
int g[N][N]; // g[i][j] = 前缀和矩阵,统计(0≤x≤i, 0≤y≤j)中满足k|C(x,y)的数对数量
// 预处理:打表组合数模k + 构建前缀和矩阵
void init()
{
// 遍历所有i(组合数上标,0≤i≤2000)
for(int i = 0; i <= 2000; i++)
{
f[i][0] = 1; // 边界条件:C(i,0)=1,mod k后仍为1
// 遍历j(组合数下标,1≤j≤i)
for(int j = 1; j <= i; j++)
{
// 杨辉三角递推:C(i,j) = C(i-1,j) + C(i-1,j-1),取模k
f[i][j] = (f[i - 1][j] + f[i - 1][j - 1]) % k;
// 计算前缀和g[i][j]:二维前缀和公式
// 公式:g[i][j] = 上侧前缀和 + 左侧前缀和 - 重复计算的左上角 + 当前位置是否符合条件
// (f[i][j]==0):当前C(i,j)能被k整除,计1;否则计0
g[i][j] = g[i - 1][j] + g[i][j - 1] - g[i - 1][j - 1] + (f[i][j] == 0);
}
// 处理j=i+1的情况:当j>i时,C(i,j)=0(无意义),前缀和继承g[i][i]
// 避免后续查询j>i时越界,统一前缀和结果
g[i][i + 1] = g[i][i];
}
}
int main()
{
int T; cin >> T >> k; // T=查询组数,k=除数
init(); // 预处理组合数和前缀和(仅需执行一次,复用所有查询)
while(T--) // 处理每组查询
{
cin >> n >> m;
// 关键:j的上限是min(n,m)(因为j≤i≤n,且j≤m)
// g[n][min(n,m)] 直接给出(0≤i≤n, 0≤j≤min(i,m))中符合条件的数对总数
cout << g[n][min(n, m)] << endl;
}
return 0;
}