目录
- [1.1 强化学习的基本结构和组成元素](#1.1 强化学习的基本结构和组成元素)
- [1.2 强化学习的特点和核心问题](#1.2 强化学习的特点和核心问题)
- [1.3 示例:多臂老虎机](#1.3 示例:多臂老虎机)
- [1.5 误差](#1.5 误差)
- [1.6 示例:OOXX](#1.6 示例:OOXX)
- Ref
1.1 强化学习的基本结构和组成元素
强化学习的三层结构
- 第一层结构(基本元素 Basic Element):
Agent、Environment、Goal - 第二层结构(主要元素 Main Element):
State、Action、Reward - 第三层结构(核心元素 Basic Element):
Policy、Value
强化学习是Agent在与环境的互动当中为了达成目标而进行的学习过程。
- 价值:表示将来能够获得所有奖励之和的期望值。
1.2 强化学习的特点和核心问题
-
强化学习的某个核心问题:
exploration(探索):是否有其他更好的行动创造更大价值
exploitation(利用):利用已有价值函数二者需要平衡
-
强化学习的特点
Trial and Error 试错
Delayed Reward 延迟奖励
1.3 示例:多臂老虎机
- 背景 :
有一个玩家Agent,环境Environment是老虎机,假设有左右两个老虎机。
该问题是强化学习中最简单的问题:因为状态只有一个,老虎机摆在那里就不会发生改变;且没有延迟奖励的问题,因为行动得到的奖励是即时的,每做出一个选择就会得到对应的奖励,不会对之后发生的事情产生任何的影响。只需要关注State-Action Value状态行动价值。 - 定义 :
定义一个行动具有的价值为对应奖励的期望值。 - 假设 :
定义行动价值的估计值为Q,实际行动价值为q。
xml
左边老虎机:
行动估计价值Q(L)
选择左边的行动价值为q(L)
奖励服从均值为500,标准差为50的正态分布N(500,50),即q(L)=500
右边老虎机:
行动估计价值Q(R)
选择右边的行动价值为q(R)
奖励服从均值为550,标准差为100的正态分布N(550,100),即q(R)=550价值函数
显然右边的老虎机是最优的选择,但是实际事先不知道这两个行动实际的价值,所以只能进行一个估计。下面需要对这两个老虎机进行尝试,利用实际获得的奖励来估计价值,最简单的方法就是用奖励的平均值作为期望值的估计,因此有如下的行动价值的估计表达式:
行动价值的估计表达式

上面这个就是Sample-average 样本平均,根据大树定律,只要对一个行动不断地去尝试,最终这个估计的平均值就会无限地接近真实的期望值。
策略函数
这里的策略函数就是选择价值最高的那个进行行动。

关于价值初始值的选择 :
这里以当前两个老虎机为例,如果设价值初始值都为0,则一开始随机选择其中一个进行行动之后,则它的价值就不为0,根据贪婪策略,下一次选择价值更高的进行行动,则一开始选择哪个老虎机之后就会一直选择它,显然是不合理的。
解决方法 :价值函数的初始值不为0,给其初始值一个很大的数值 ,这样选择任何一个行动之后,它的价值反而会变小,这就使得算法会去尝试其他的行动。这样通过初始值的适当选择,使得贪婪策略也能够进行足够的exploration。
PS:当价值的初始值为0时,这个初始值是不计入之后的平均计算的,也就是说任何行动尝试了一次之后,就用实际获得的奖励值替代了初始值,这样如果选择了一个很高的初始期望值,同样不把它计入之后的平均计算,实际的结果就相当于所有的行动都尝试一遍再采取贪婪的选择。
但这里的方法是把这个初始值也计入之后的平均计算,如果不计入,相当于所有的行动都只探索一遍,如果计入,则会鼓励更多次的探索行为。
但这里只适用于状态不会发生改变的情况,一旦考虑状态会发生改变的情况,上面这个方法(贪婪策略)也是不可行的。所以需要引入一个新的策略(ε-Greedy:在大部分情况下是贪婪的,但有一定的概率ε做出随机的选择 ),这样即可保证每次的行动都有一定的探索,即使状态会发生变化,当然ε的选择并不是唯一的,根据不同的场景值也不同,也可以根据时间的选择动态调整ε的值。
K-armed Bandit 强化学习过程
xml
K-armed Bandit
当前两个老虎机,采用ε=0.1,初始值为998的强化学习方法。
t=1:左右两个老虎机选择的价值相同,Q(L)=Q(R)=998,此时随机做出左边这个选择,得到的奖励q(L)=526,此时左边的价值更新,右边不变:
Q(L)=(998+526)/ 2 = 762,Q(R)=998
t=2:右边的选择价值更高,得到的奖励q(R)=518,此时右边的价值更新,左边不变
Q(L)=(998+518)/ 2 = 762,Q(R)=(998+518)/ 2 = 758
t=3:左边的选择价值更高,得到的奖励q(L)=460,此时左边的价值更新,右边不变
Q(L)=(998+526+460)/ 3 = 661,Q(R)=(998+518)/ 2 = 758
t=4:右边的选择价值更高,得到的奖励q(R)=430,此时右边的价值更新,左边不变
Q(L)=(998+526+460)/ 3 = 661,Q(R)=(998+518+430)/ 3 = 649
t=5:左边的选择价值更高,但是由于 ε-Greedy 生效了,此时还是选择右边,得到的奖励q(R)=682,此时右边的价值更新,左边不变
Q(L)=(998+526+460)/ 3 = 661,Q(R)=(998+518+430+682)/ 4 = 657
.
.
.
t=n,最终左右两边都会收敛到真实值500和5501.5 误差
误差的来源
- 前面几小节中老虎机的问题就是用Sample Average样本平均来估计价值的方法,函数如下:
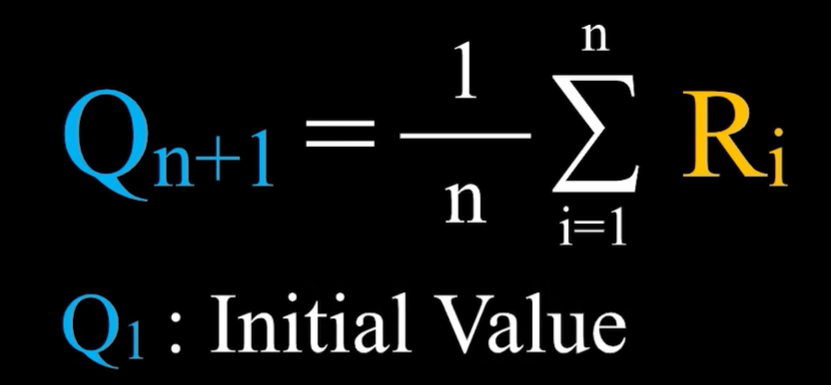
Qn+1指的是在采取这个行动n次之后,得到了n次对应的奖励之后对这个行动价值的估计值,即这n次奖励的平均。
公式变换
- 将上面的公式进行推导换一种形式:
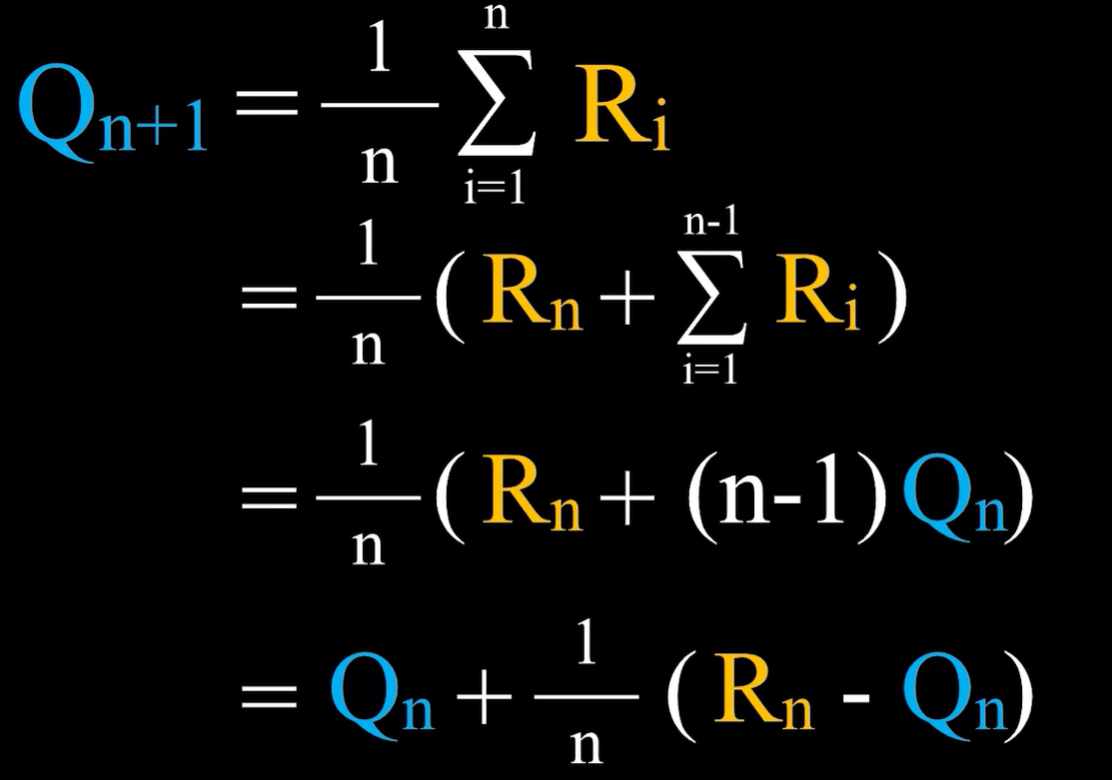


样本平均法中,步长为1/n ,这也就意味着随着采取这个行动的次数增加,误差对于学习的影响会越来越小。
但存在一个问题:如果这个行动对应的奖励分布会随着时间发生变化,那应该随时根据误差来调整对于价值的估计,因此不希望学习率越来越小。
我们将学习率1/n变为常数α ,得到以下公式:
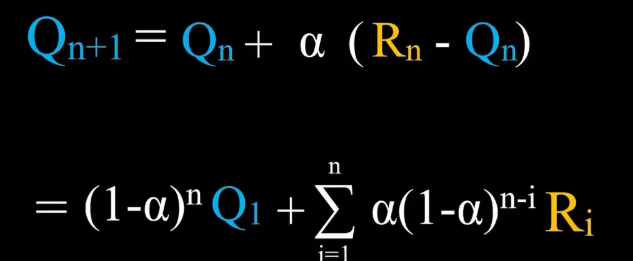
此时对于价值的估计已经不再是实际得到的奖励的平均值了,而是一个加权平均值,并且时间越早得到的奖励权重越小,即更看重最近得到的奖励,显然当前的算法更加适用于奖励分布可能会发生改变的情况。
算术平均和加权平均
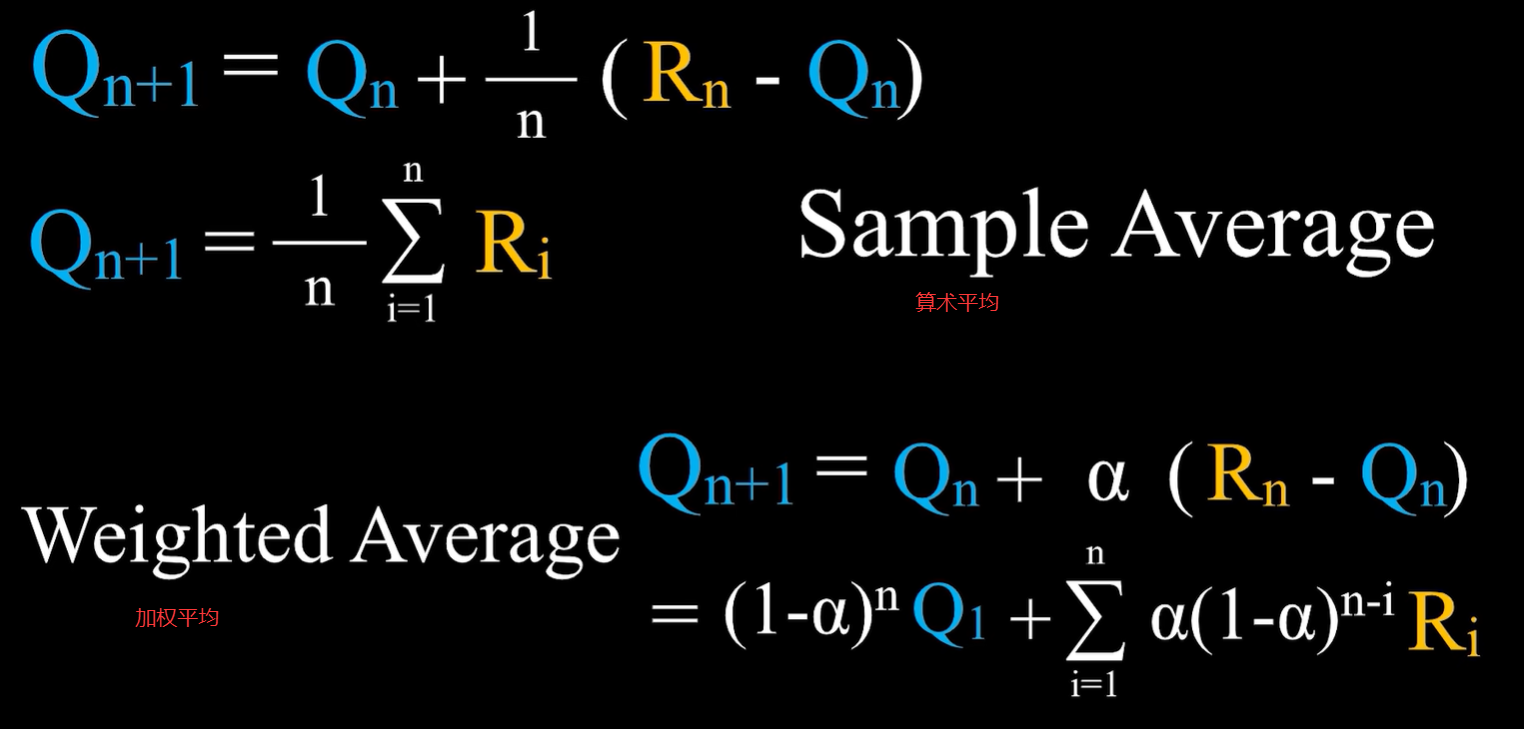
在算术平均中,价值的初始估计值Q1对于之后的价值估计是没有影响的;而在加权平均中,价值的初始估计值Q1对于之后的价值估计是有影响的。
在前面的老虎机强化学习中,所用到的是带有初始值的算术平均。
1.6 示例:OOXX
示例说明:tic tac toe(井字游戏)

理论公式推导
- 上一小节中
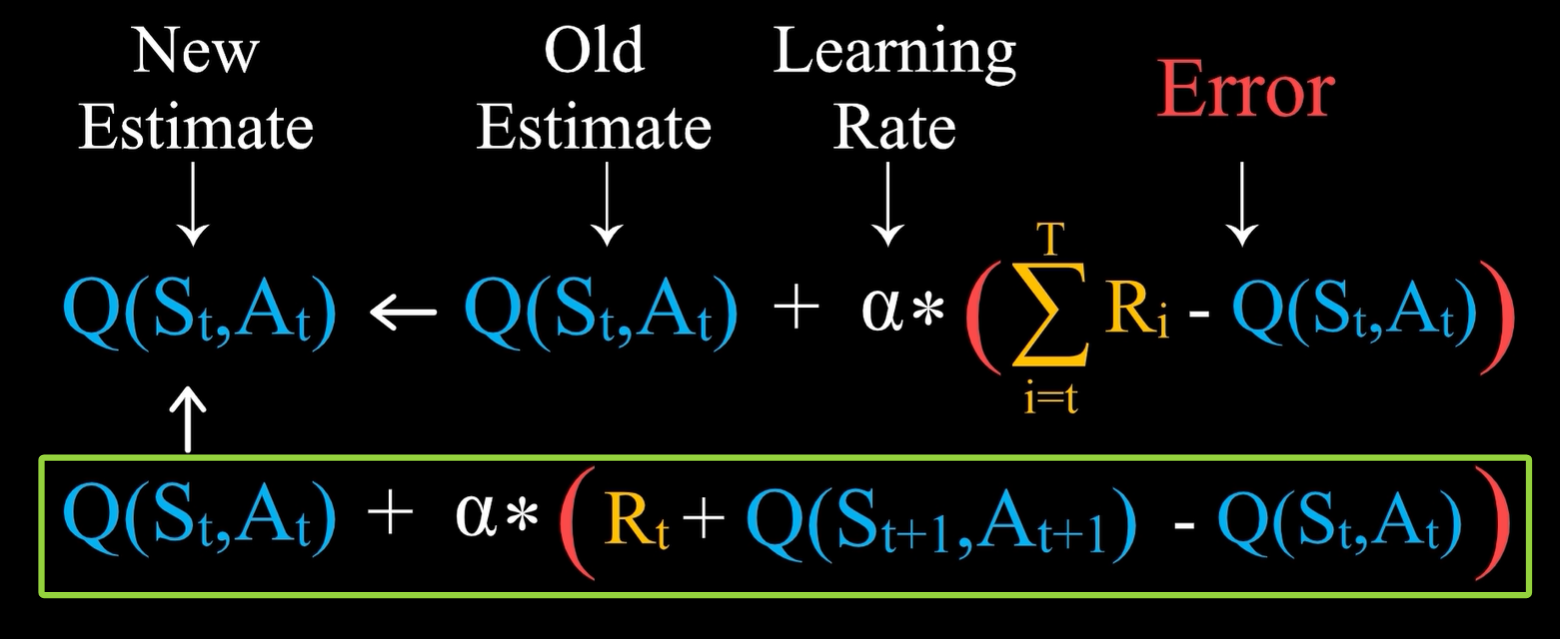
行动价值的学习公式:新的估计 = 旧的估计 + 学习率 * 误差,它适用于没有延迟奖励,只有一个状态的情况,将上面的公式推广到状态价值或者状态行动价值。
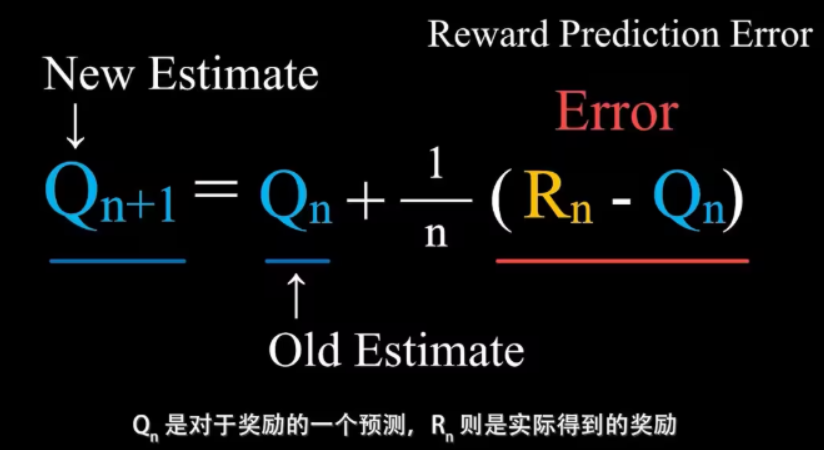
- 下面是一个完整的强化学习过程
右边的红色矩形框:从t时刻处于状态St开始,玩家采取了行动At,得到奖励Rt,并且进入到下一个状态St+1,进而采取行动At+1,得到奖励Rt+1,如此进行下午,不妨假设在状态ST+1时游戏结束。
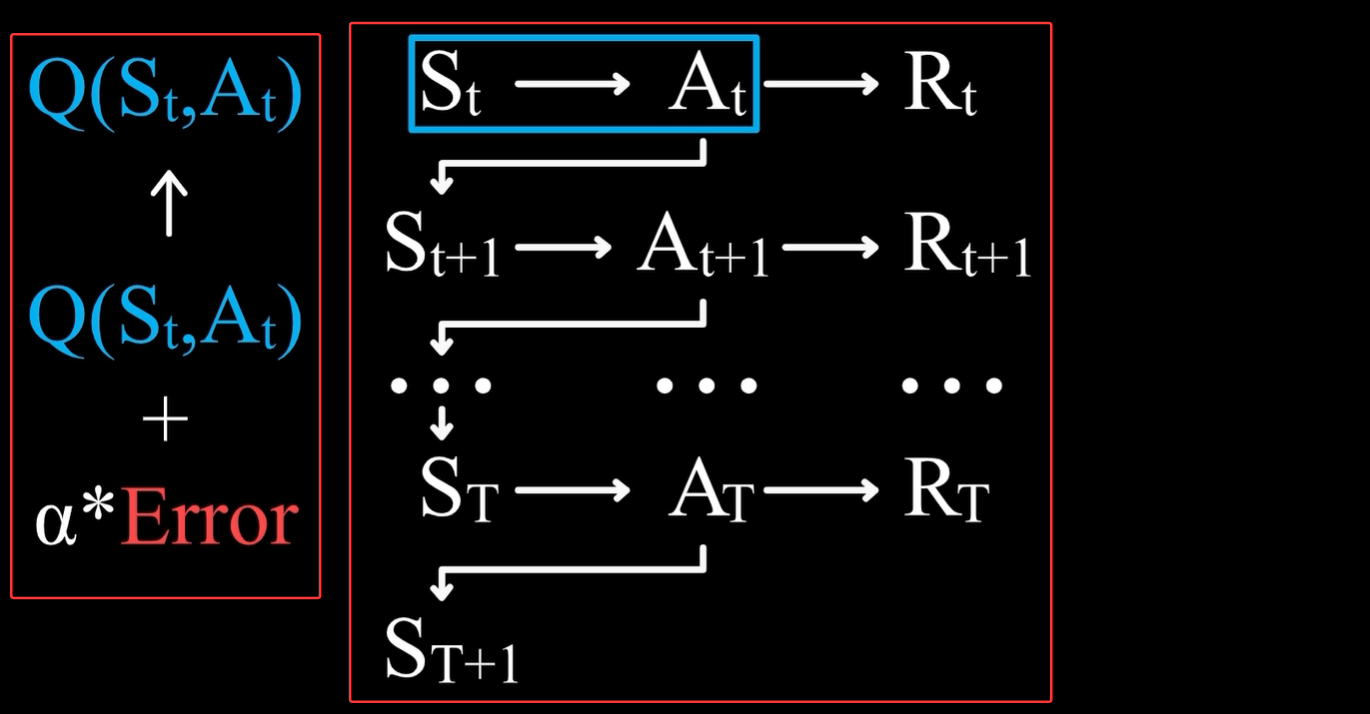
左边的红色矩形框:Q(St,At) 代表在 St 状态下,采取At行动后,产生的价值Rt的估计,那么旧估计的误差自然就是旧估计Q(St,At) - t 时刻后所有奖励Rt。 - 针对上图中左边的红色矩形框,问题在于如何表示误差Error
因为价值的定义是未来所能得到的所有奖励之和的估计值,则误差表示实际得到的奖励之和和旧估计之间的差值 ,即下面绿色矩形框中的内容。
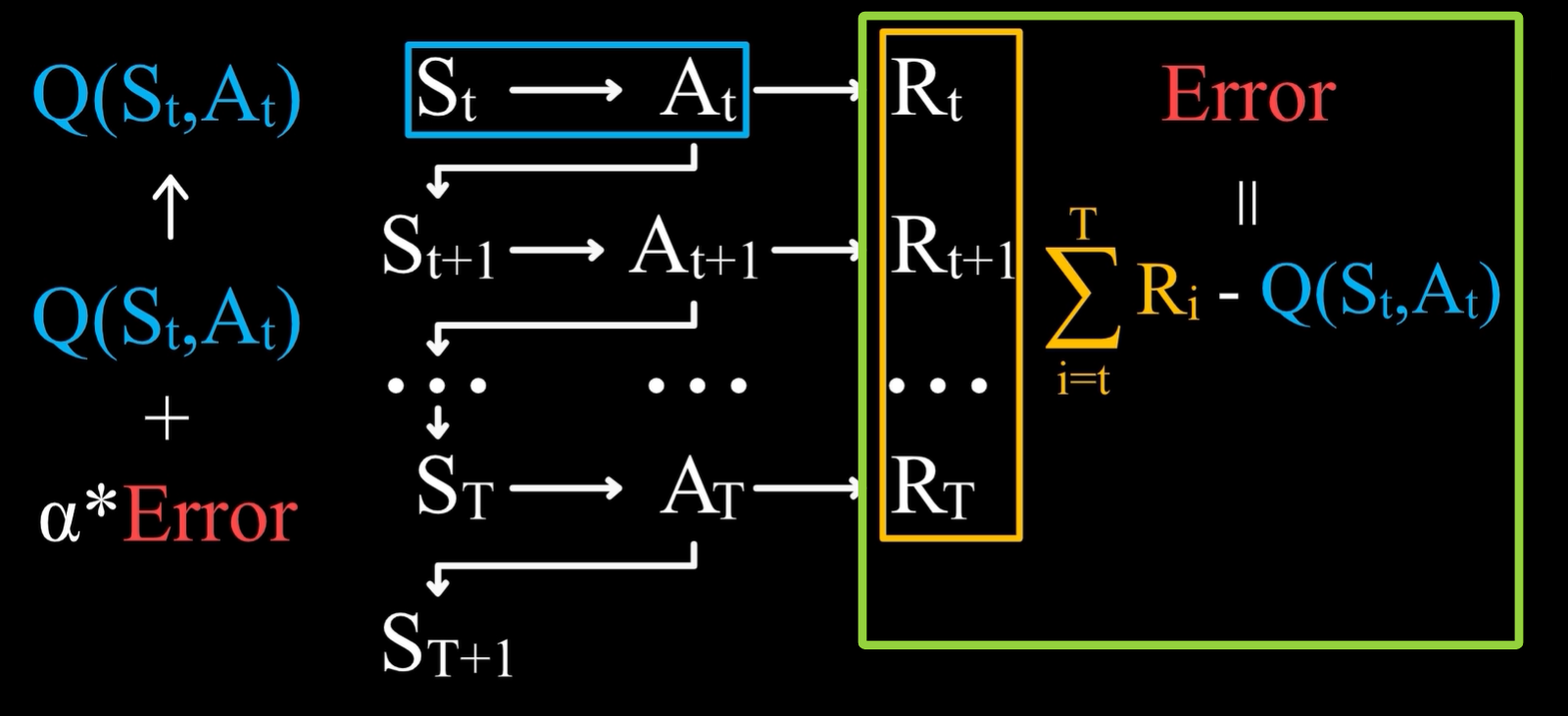
- 将上面的强化学习过程整合后,就得到了如下的状态行动价值的学习表达式:
即在St状态下,采取了At这一行动之后,直到游戏结束,将实际得到的奖励之和减去旧估计值,就得到了误差。

- 从t时刻开始直到游戏结束所获得的奖励之和,等于Rt加上从t+1时刻开始直到游戏结束所获得的奖励之和,后面这一项可以用已经有的估计值来替代实际值,即Q(St+1,At+1)
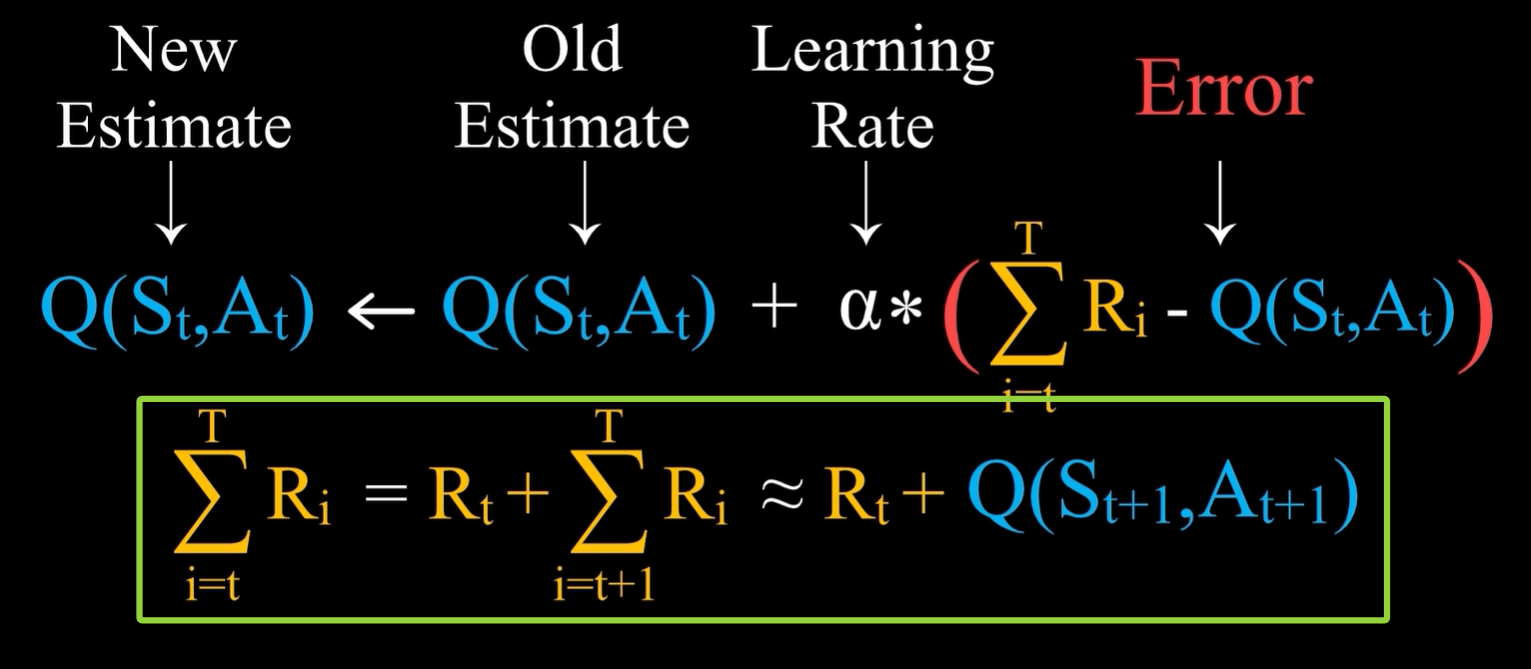
- 这样不需要等到游戏结束就可以计算Q(St,At)的新估计值,即绿色矩形框表示 Monte Carlo Methods 蒙特卡洛方法 的雏形;上面的式子则是 Temporal-Difference Learning 时序差分学习法 的雏形。
- 将上面的的推理过程总结如下:
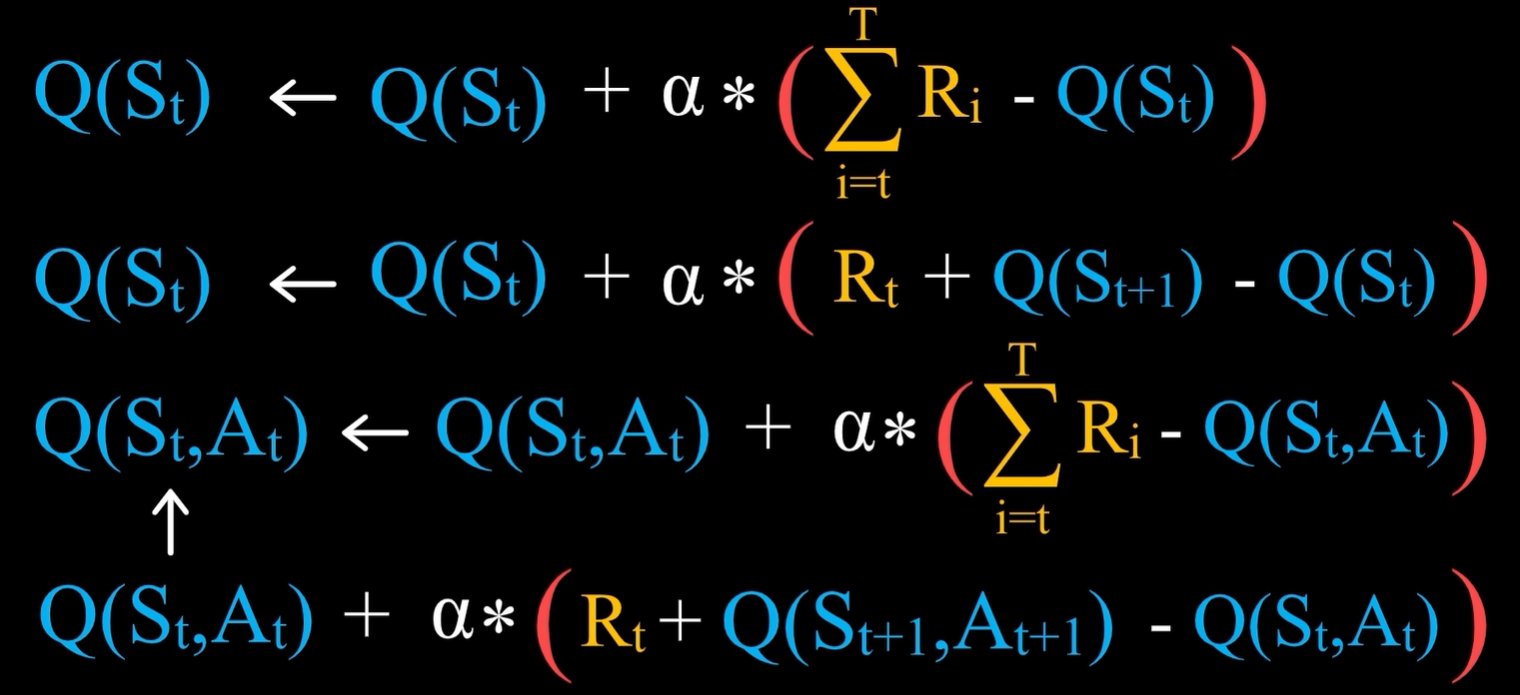
- 有了上面这些公式,再加上
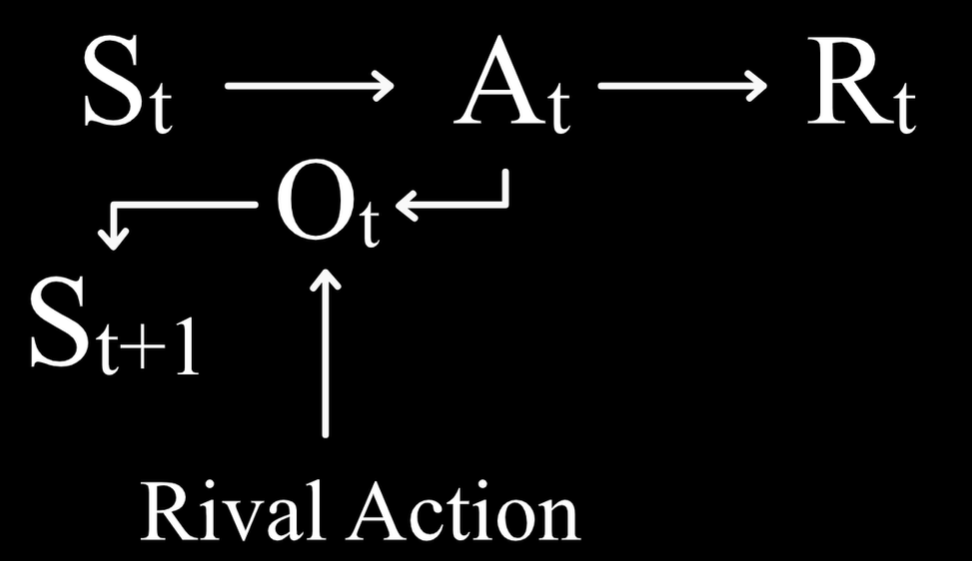
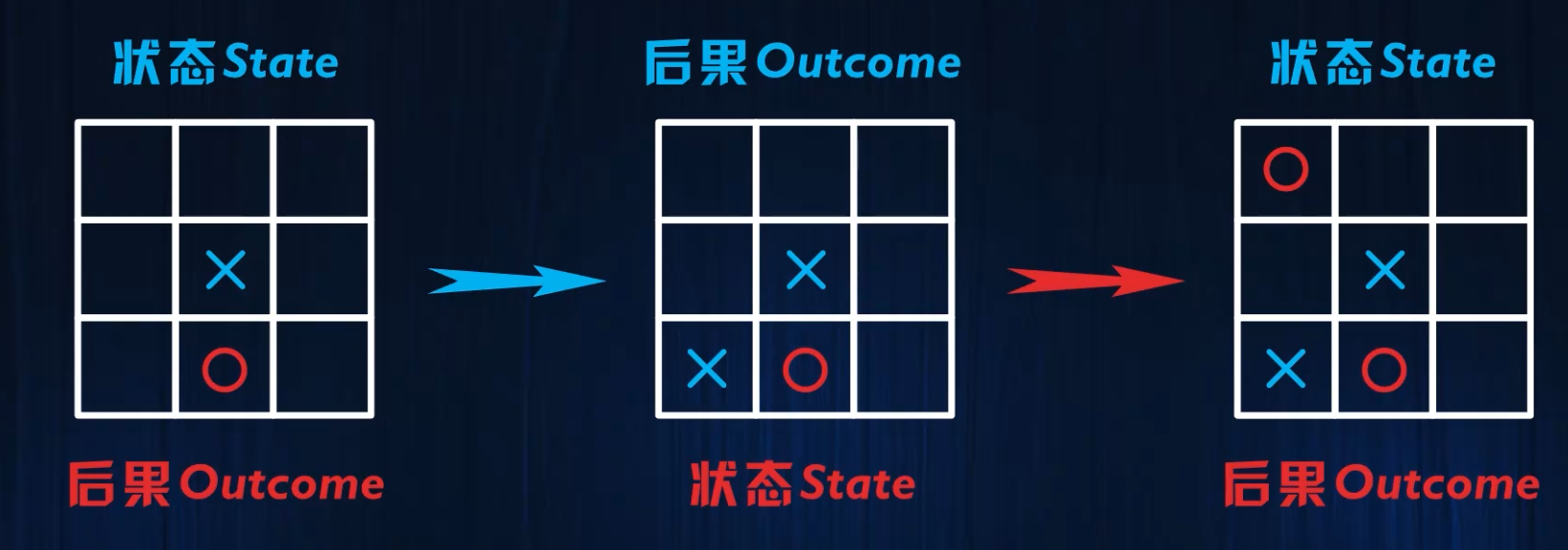
ε-Greedy的策略,现在可以选择去学习价值函数,那么行动就应该是选择能够进入价值最高的状态那一个,但这里存在一个问题,玩家进入什么状态不仅仅是由玩家自己的行动决定的,还取决于对手的行动,所以要依据价值来决定行动的话,玩家需要对对手的行动有一个预测。需要能够学习一种能够直接指导行动,数量又比较少的价值,在棋牌类游戏中,引入新的概念,Outcome即Afterstate,表示玩家行动的后果对于对手来说是一种状态。
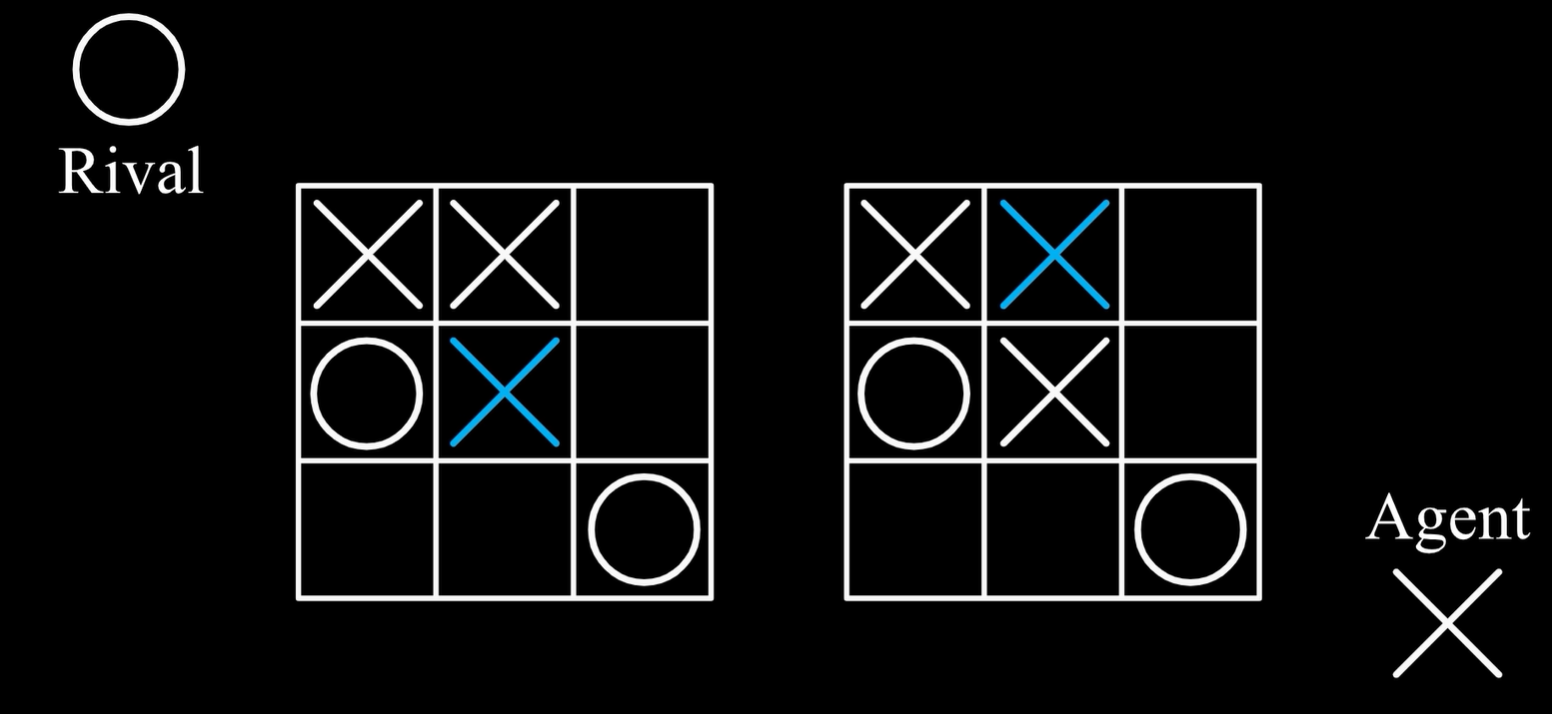
即下面这两种情况,玩家在不同的位置落子,后果是一样的,则这两种状态行动对的价值应该也是一样的,所以只需要去学习这个后果的价值,所用到的学习公式和状态价值或者状态行动价值是完全相同的。
代码实现
- 状态向量每一个位置的值,就是价值矩阵对应维度的索引
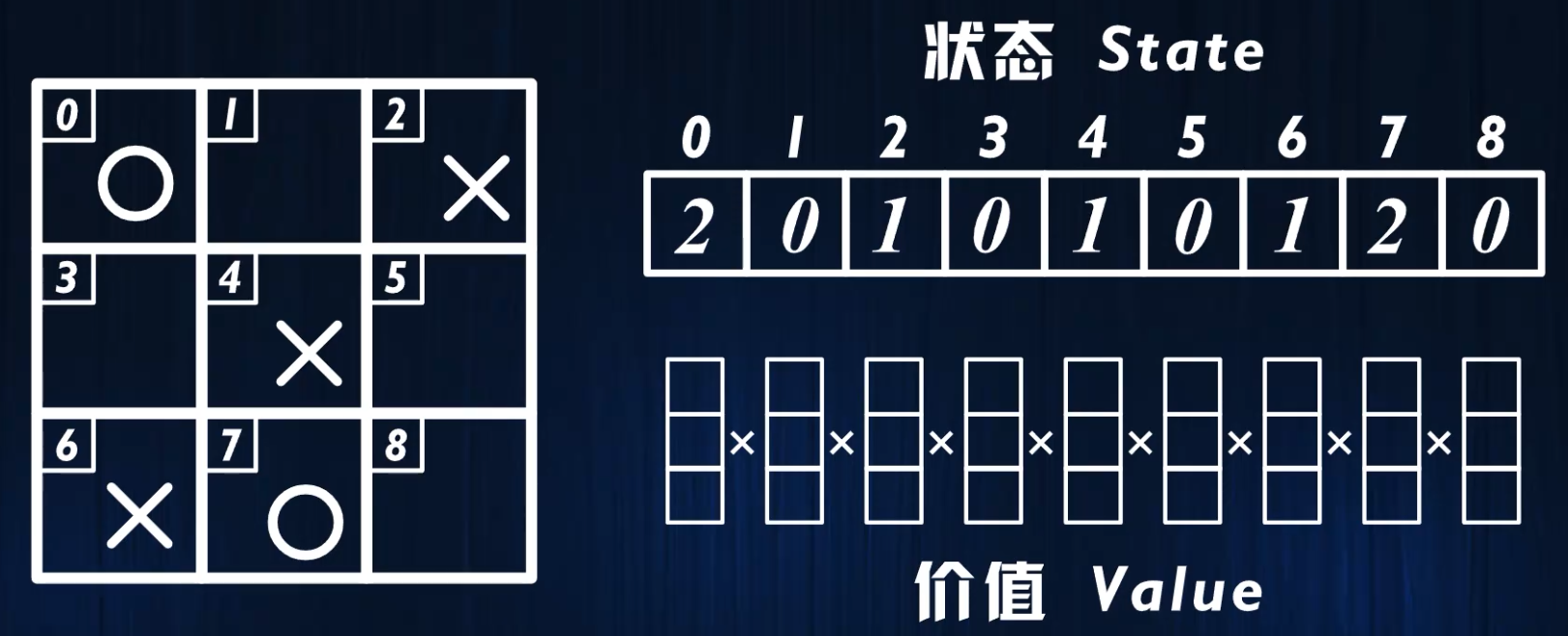
例如下面这个状态的价值,就存储在价值矩阵当中坐标为[2,0,1,0,1,0,1,2,0]的位置
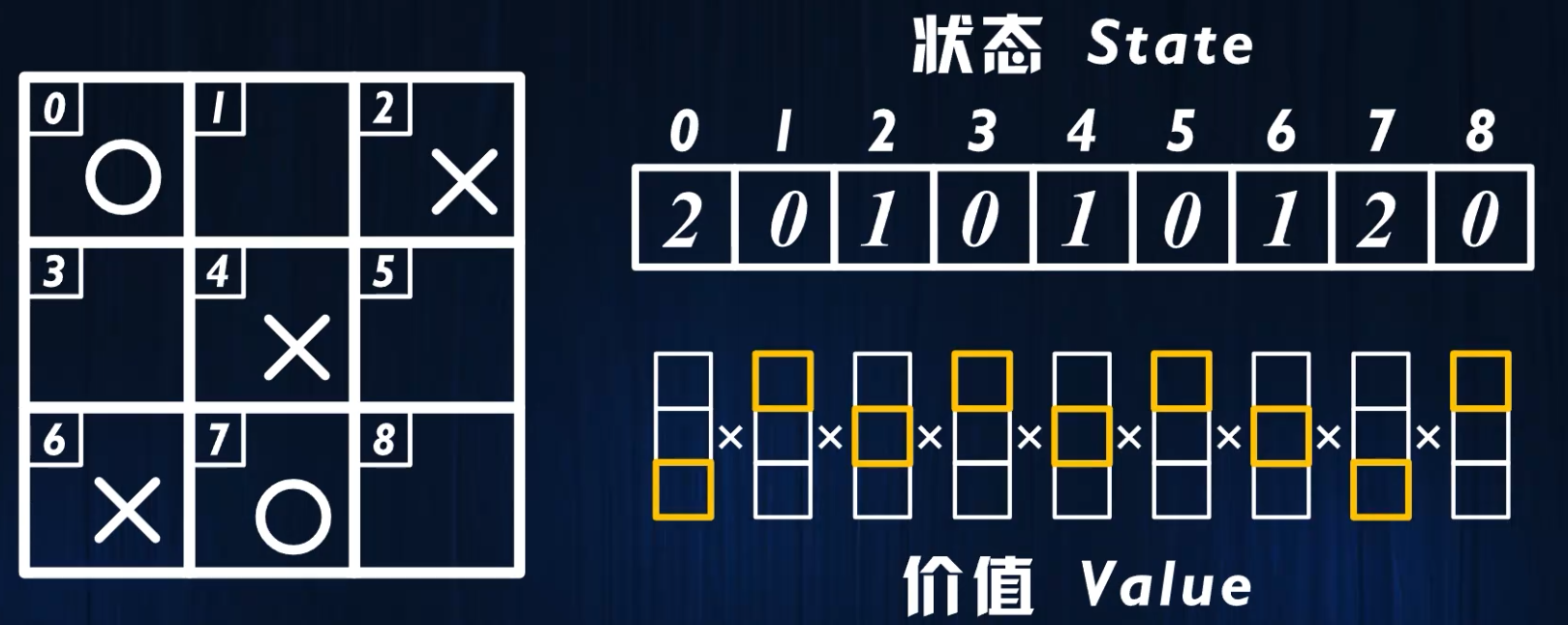
- 下图中,在第一个棋盘中,X玩家做出行动之后,在第二个棋盘的情况下,O玩家需要做出行动,因此第二个棋盘对于O玩家来说就是状态 ,但是对于X玩家来说并不是状态,将其称为后果 ,也就是X玩家做出一个行动之后导致的后果,一个玩家的后果对于另一个玩家来说是状态,反之亦然。
强化学习中,最好去学习后果的价值,等价于状态-行动对的价值,得到后果的价值之后,只需要在一个状态下,选择后果的价值最大的行动,具体学习价值的算法则采用基于误差的学习法。
ooxx_rl.py
python
import numpy as np
import matplotlib.pyplot as plt
# 因为我们之后需要创建两个 Agent 互相下棋,所以定义一个 Agent 的类会方便一点
class Agent():
def __init__(self, OOXX_Index, Epsilon, Alpha):
self.index = OOXX_Index # OOXX_Index 用 1 或者 2 代表是两个 Agent 当中的哪一个
self.epsilon = Epsilon # Epsilon 就是 ε-Greedy 策略中的随机选择概率
self.alpha = Alpha # Alpha 就是学习率
self.value = np.zeros((3,3,3,3,3,3,3,3,3)) # 储存状态价值的表,创建一个9维的全零数组,即3^9
# OOXX的棋盘一共有 9 个位置,每个位置有 3 种情况(O、X、无)
# 所以我们用一个 9 维的向量来表示状态,每个维度表示一个位置上的 3 种情况
# 想像一下我们用一个 361 维向量来表示围棋的状态,这个向量会非常巨大
# 在实际上不可行,所以对于状态空间非常大的情况我们需要别的表示状态的方法
# 例如使用深度神经网络 (具体可以参考 AlphaGo 的视频 https://www.bilibili.com/video/BV1hb4y197he)
self.stored_Outcome = np.zeros(9).astype(np.int8) # Agent 内部记录的后果outcome,初始化为 0,表示空棋盘
# 因为要将后果作为价值矩阵的索引,所以用 .astype(np.int8) 规定为整数
# 重置状态:在每次完成一局游戏后,需要重置状态
def reset(self):
self.stored_Outcome = np.zeros(9).astype(np.int8)
# 策略函数:输入为状态,输出为后果,同时进行价值更新
def move(self, State):
Outcome = State.copy() # 拷贝一份状态
# 因为这个状态 State 对另一名玩家来说是后果
# 需要留着用来学习价值,所以不能直接更改,因此 .copy() 拷贝一份
available = np.where(Outcome==0)[0] # 先判断棋盘上有哪些地方可以落子,也就是 Outcome==0 的地方
if np.random.binomial(1, self.epsilon): # 判断要不要采取 ε-Greedy 的随机行动;表示伯努利试验的实现,仅模拟1次成功概率10% 的二值随机事件
Outcome[np.random.choice(available)] = self.index # 随机选择一个位置标注为 1 或着 2 (取决于是 Agent1 还是 Agent2)
else: # 如果不随机,就采用最优策略:需要遍历所有可能的行动以及它们所有可能导致的后果,然后来计算它们的价值,选出价值最大的。
temp_Value = np.zeros(len(available)) # 创建一个临时的价值向量
for i in range(len(available)): # 对每一个可能落子的地方
temp_Outcome = Outcome.copy() # 拷贝当前时刻的状态
temp_Outcome[available[i]] = self.index # 假设在一个地方落子,得到后果
temp_Value[i] = self.value[tuple(temp_Outcome)] # 调用价值函数,计算得到的后果的价值(tuple将其换成元组类型,作为self.value索引来得到价值)
choose = np.argmax(temp_Value) # 选择价值最大的那一个行动
Outcome[available[choose]] = self.index # 把选择的那个位置标注为 1 或着 2 (取决于是 Agent1 还是 Agent2)
# 基于误差的学习法,或者说就是时序差分法公式 (在这个例子中即时奖励为 0)
Error = self.value[tuple(Outcome)] - self.value[tuple(self.stored_Outcome)]
# 计算当前的后果的价值估计和储存的(上一个)后果的价值估计的误差
self.value[tuple(self.stored_Outcome)] += self.alpha*Error # 更新储存的(上一个)后果的价值估计
self.stored_Outcome = Outcome.copy() # 把当前的后果储存(因为接着就要进行下一步了)
return Outcome # 返回当前的后果
# 写一个函数判断输赢:直接用暴力枚举判断输赢(赢得条件就是将三个棋子连城一条线)
def Judge(Outcome, OOXX_Index): # 输入为状态和对应的玩家
Triple = np.repeat(OOXX_Index, 3)
winner = 0 # 默认胜负未分
if 0 not in Outcome: # 棋盘中没地方下了
winner = 3 # 平局
if (Outcome[0:3]==Triple).all() or (Outcome[3:6]==Triple).all() or (Outcome[6:9]==Triple).all(): # 分别判断三行,.all() 表示数组中所有元素是否都为 True
winner = OOXX_Index
if (Outcome[0:7:3]==Triple).all() or (Outcome[1:8:3]==Triple).all() or (Outcome[2:9:3]==Triple).all(): # 分别判断三列
winner = OOXX_Index
if (Outcome[0:9:4]==Triple).all() or (Outcome[2:7:2]==Triple).all(): # 分别判断两条对角线
winner = OOXX_Index
return winner # 返回玩家是否胜利
if __name__ == '__main__':
# 创建两个 Agent(可以自己改变参数)
Agent1 = Agent(OOXX_Index = 1, Epsilon=0.1, Alpha=0.1)
Agent2 = Agent(OOXX_Index = 2, Epsilon=0.1, Alpha=0.1)
Epoch = 30000 # 训练 3 万次
Winner = np.zeros(Epoch) # 记录结果
for i in range(Epoch):
if i==20000: # 在 2 万次之后取消掉随机性
Agent1.epsilon = 0
Agent2.epsilon = 0
Agent1.reset() # 重置状态
Agent2.reset() # 重置状态
winner = 0 # 默认胜负未分
State = np.zeros(9).astype(np.int8) # 初始化棋盘
# 我们默认 Agent1 先行
# 并且以 Agent1 的视角定义 State 和 Outcome
while winner == 0: # 如果胜负未分
Outcome = Agent1.move(State) # Agent1 采取行动,并且更新价值
winner = Judge(Outcome, 1) # 判断 Agent1 是否获胜
if winner == 1: # 如果 Agent1 获胜
Agent1.value[tuple(Outcome)] = 1 # 因为Agent1获胜了,所以 Outcome 的价值对 Agent1 来说为 1
Agent2.value[tuple(State)] = -1 # Agent2 对应的后果,也就是 Agent1 面临的 State 的价值对 Agent2 来说为 -1,因为Agent2 输了
elif winner == 0: # 如果胜负未分
State = Agent2.move(Outcome) # Agent2 采取行动,并且更新价值
winner = Judge(State, 2) # 判断 Agent2 是否获胜
if winner == 2: # 如果 Agent2 获胜
Agent2.value[tuple(State)] = 1 # Agent2 对应的后果,也就是 Agent1 面临的 State 的价值对 Agent2 来说为 1
Agent1.value[tuple(Outcome)] = -1 # Outcome 的价值对 Agent1 来说为 -1
Winner[i] = winner # 记录结果
# 根据结果计算胜率
step = 250 # 每隔250局游戏计算一次胜率
duration = 500 # 胜率根据前后共500局来计算
def Rate(Winner):
Rate1 = np.zeros(int((Epoch-duration) / step) +1) # Agent1 胜率
Rate2 = np.zeros(int((Epoch-duration) / step) +1) # Agent2 胜率
Rate3 = np.zeros(int((Epoch-duration) / step) +1) # 平局概率
for i in range(len(Rate1)):
Rate1[i] = np.sum(Winner[step*i:duration+step*i]==1)/duration
Rate2[i] = np.sum(Winner[step*i:duration+step*i]==2)/duration
Rate3[i] = np.sum(Winner[step*i:duration+step*i]==3)/duration
return Rate1,Rate2,Rate3
Rate1, Rate2, Rate3 = Rate(Winner)
fig,ax=plt.subplots(figsize=(16,9))
plt.plot(Rate1,linewidth=4, marker='.', markersize=20, color="#0071B7", label="Agent1")
plt.plot(Rate2,linewidth=4, marker='.', markersize=20, color="#DB2C2C", label="Agent2")
plt.plot(Rate3,linewidth=4, marker='.', markersize=20, color="#FAB70D", label="Draw")
plt.xticks(np.arange(0,121,40),np.arange(0,31+1,10),fontsize=30)
plt.yticks(np.arange(0,1.1,0.2),np.round(np.arange(0,1.1,0.2),2),fontsize=30)
plt.xlabel("Epochs(x1k)",fontsize=30)
plt.ylabel("Winning Rate",fontsize=30)
plt.legend(loc="best",fontsize=25)
plt.tick_params(width=4,length=10)
ax.spines[:].set_linewidth(4)
plt.show()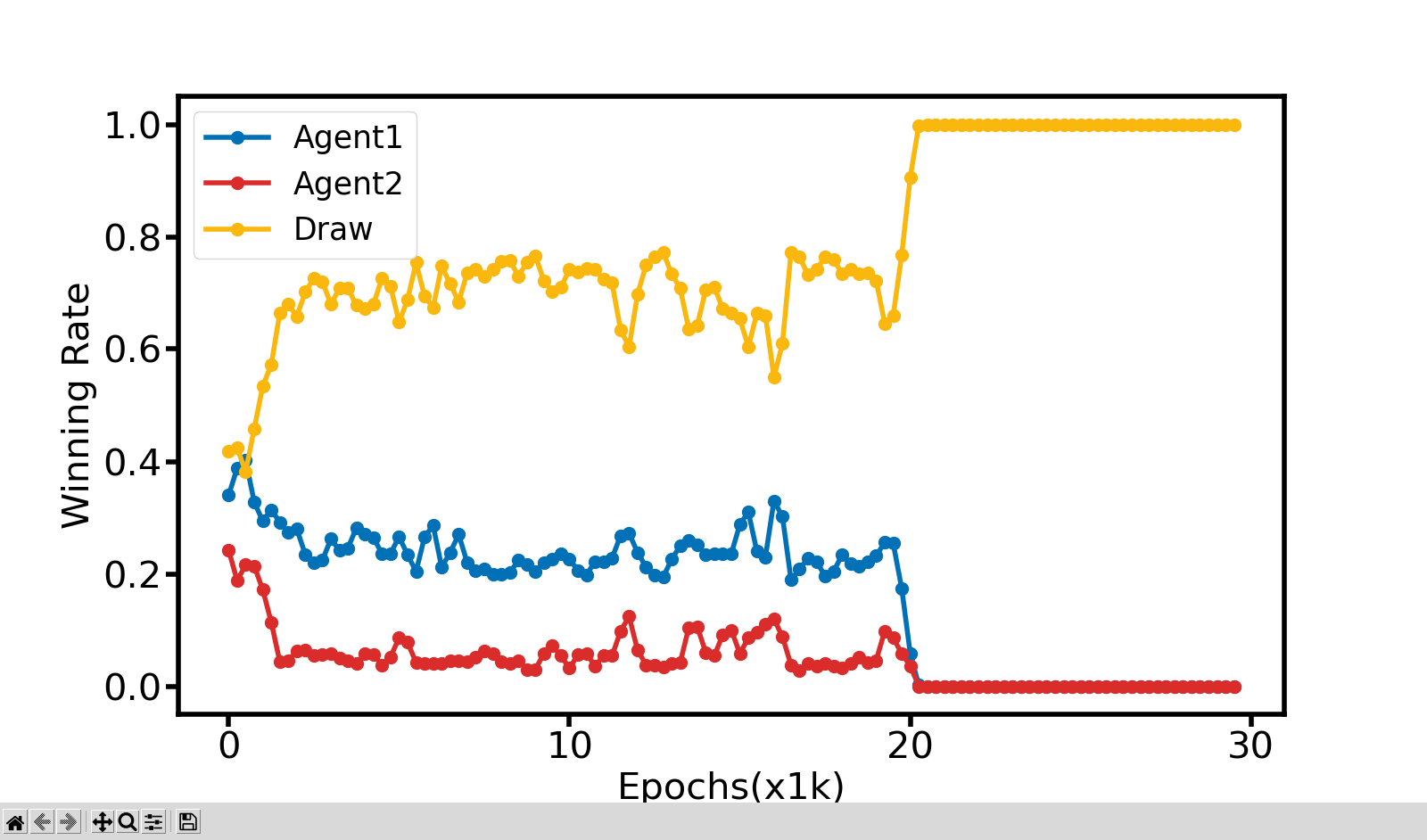
胜率图上可以看到,由于20000次以前,因为有ε-Greedy 策略的原因,Agent1和Agent2各有来去,并且OOXX的游戏由于先手有更高的胜率,代码中默认也是Agent1先手的,符合逻辑;20000次以后,因为取消了ε-Greedy 策略,两边都是朝着价值最高的方向进行行动,所以导致每次都是和棋。