从项目入手机器学习——（四）特征工程（简单特征探索）

仍然用之前提到的泰坦尼克号数据集来进行特征工程，不同的是，本次从kaggle加载数据集，并尝试在该竞赛中拿到一个好的成绩（数据集）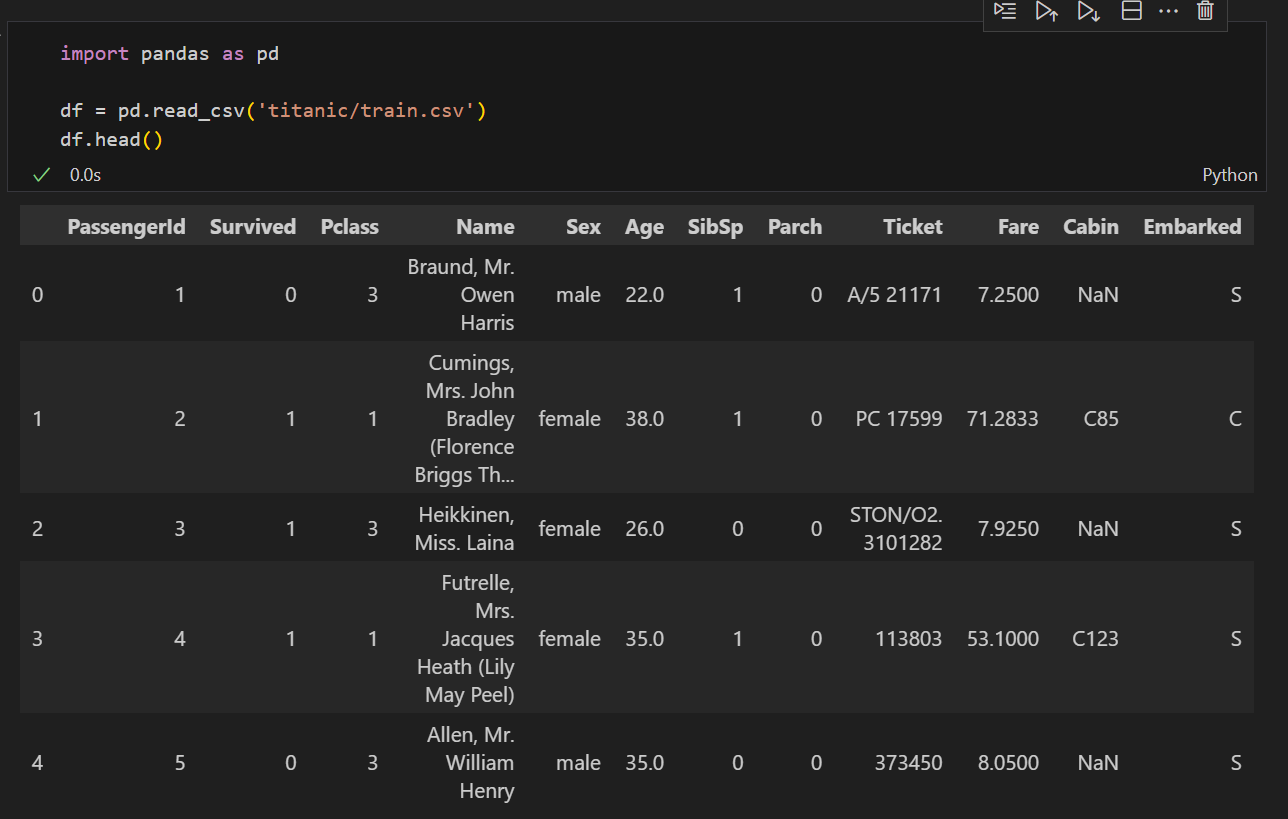

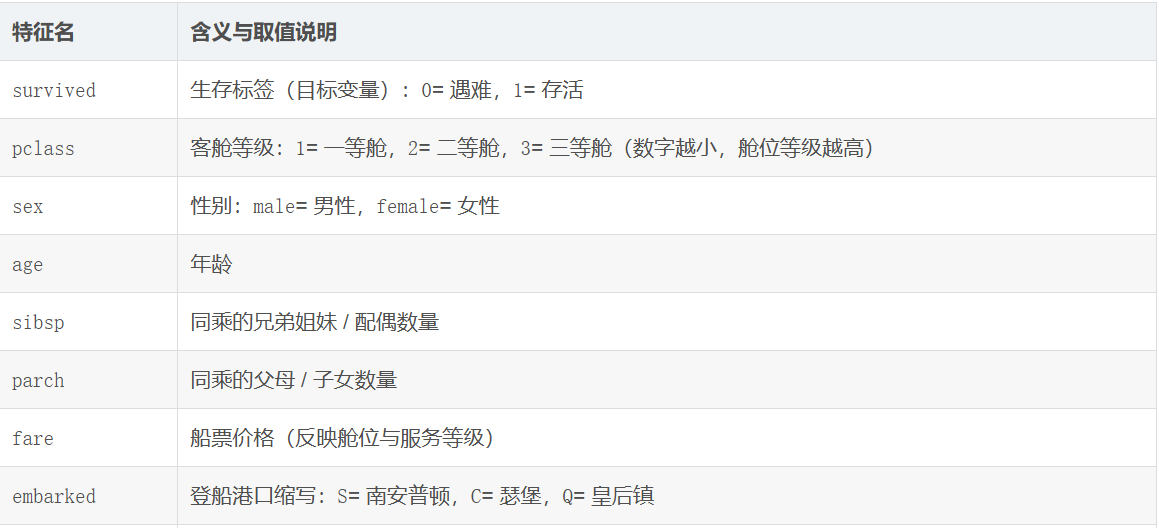
该数据集和season中基本一致，但特征少了一部分，因此做起来更简单一些，大致特征含义如下

数据预处理

python 复制代码

# 检查缺失值
print("缺失值统计：")
print(df.isnull().sum())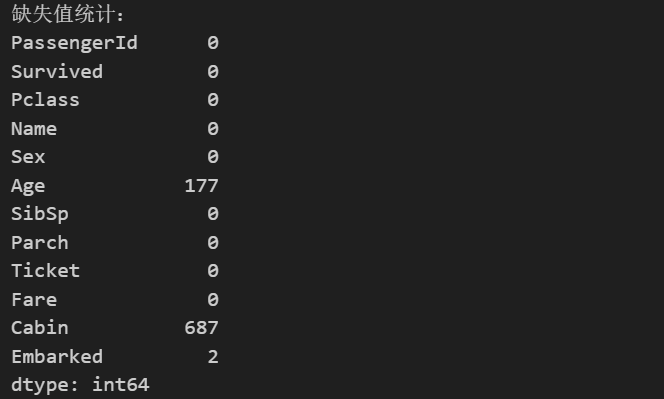

python 复制代码

# 处理缺失值
# Age 用中位数填充
df['Age'] = df['Age'].fillna(df['Age'].median())

# Embarked 用众数填充
df['Embarked'] = df['Embarked'].fillna(df['Embarked'].mode()[0])

# 删除 Cabin 列，如果存在的话
if 'Cabin' in df.columns:
    df.drop('Cabin', axis=1, inplace=True)

print("处理缺失值后：")
print(df.isnull().sum())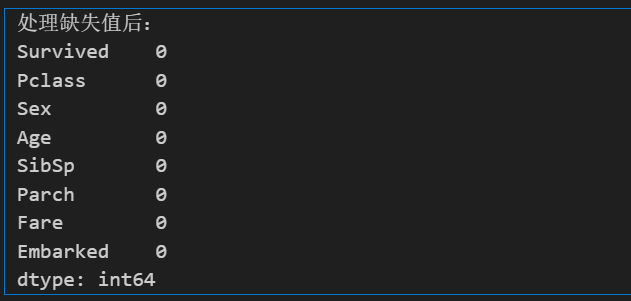

一般的数据集在这里还需要进行异常值处理，但是泰坦尼克数据集是一个来自真实的数据集，因此为了保证模型的鲁棒性，不需要这一步。

python 复制代码

# 编码分类变量
# Sex: male=0, female=1
df['Sex'] = df['Sex'].map({'male': 0, 'female': 1})

# Embarked: S=0, C=1, Q=2
df['Embarked'] = df['Embarked'].map({'S': 0, 'C': 1, 'Q': 2})

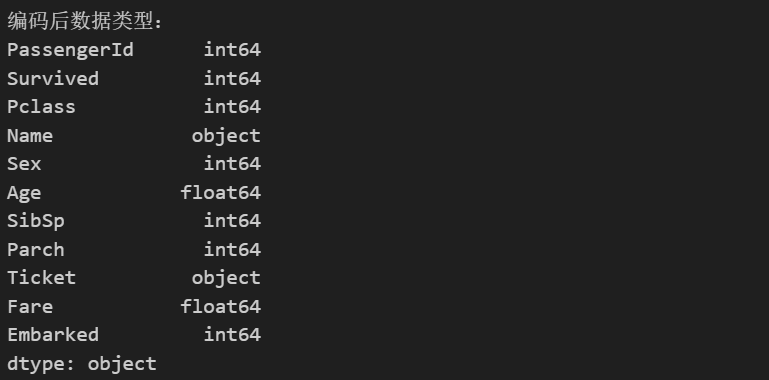
print("编码后数据类型：")
print(df.dtypes)

到这里其实通过经验我们可以判断，某些标签对是否存活大概率是没有影响的（如姓名、票名、乘客序号），因此可以去除（当然，也许有很小的可能有影响，后续的特征工程可以进行判断）。此外i，Survived是预测标签，也应去除。

python 复制代码

# 删除不必要的列
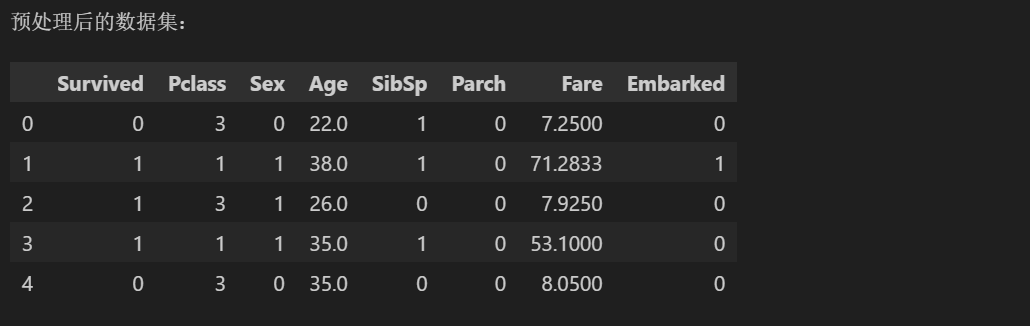
X.drop(['PassengerId', 'Name', 'Ticket'], axis=1, inplace=True)
print("预处理后的数据集：")
X.head()

特征探索

python 复制代码

# 描述性统计
print("数据集描述性统计：")
df.describe()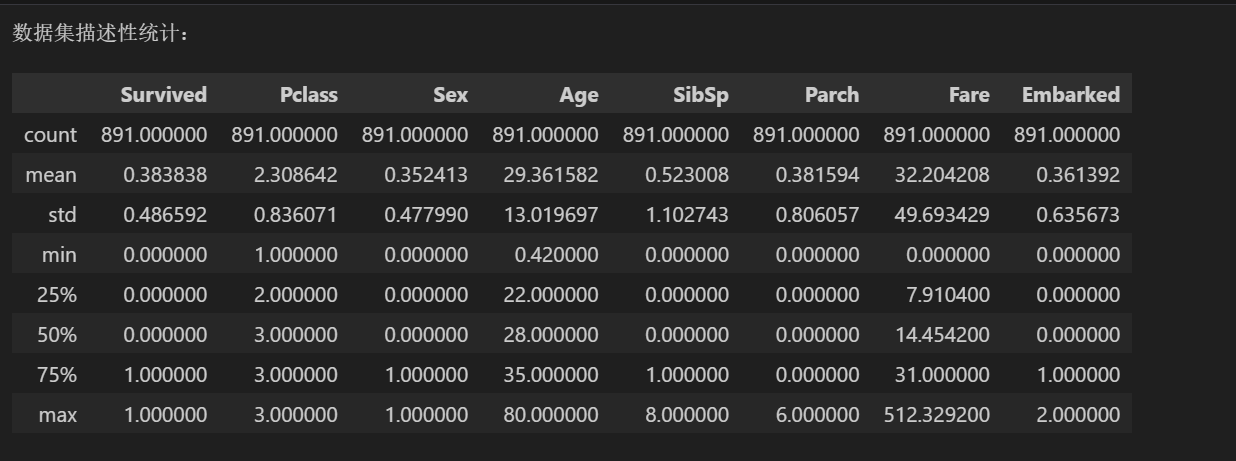

数值特征

定义：表示数量或度量的特征，取连续或离散数值，如年龄、价格、分数。
类型：连续（实数，如体重）、离散（整数，如人数）。
处理：标准化、归一化，用于回归或需要尺度敏感的模型。

分类特征

定义：表示类别或标签的特征，取离散值，如性别、颜色、港口。
类型：名义（无顺序，如颜色）、有序（有顺序，如等级）。
处理：编码为数值（如 one-hot 或 label encoding），用于分类模型。

因此，在进行数值特征分析时，基本有分类特征的输出，但其没有参考价值，分类特征同理。

数值特征分析

特征相关性矩阵

python 复制代码

# 相关性矩阵
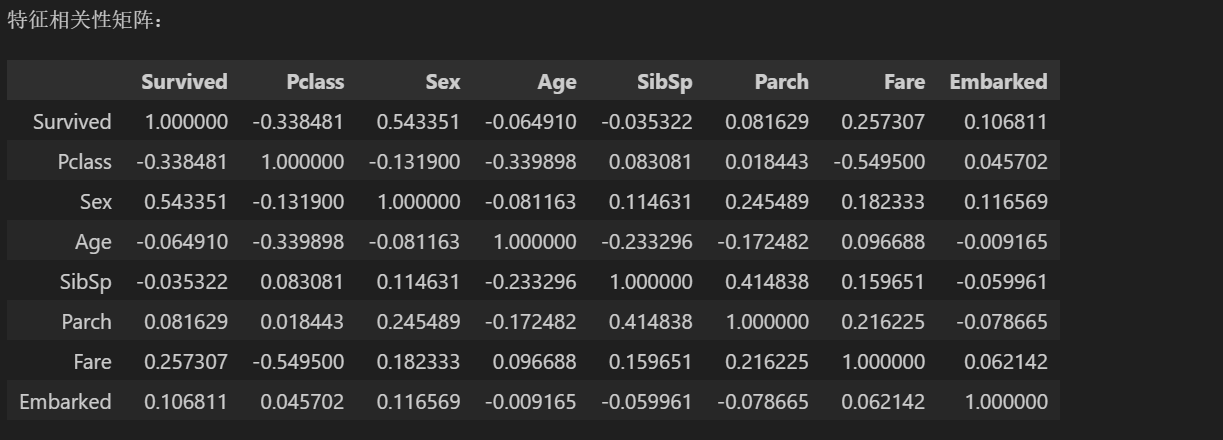
print("特征相关性矩阵：")
correlation_matrix = df.corr(numeric_only=True)
correlation_matrix

基本概念

相关系数：范围从 -1 到 1
- 1：完全正相关（一个增加，另一个也增加）
- -1：完全负相关（一个增加，另一个减少）
- 0：无相关性
绝对值越大，相关性越强。通常：
- 0-0.3：弱相关
- 0.3-0.7：中等相关
- 0.7-1.0：强相关

相关性矩阵主要用来探索不同特征与目标特征（本数据集是Survived）之间的关系，可以看到，相关性最高的是Sex性别，sibsp（同乘的兄弟姐妹 / 配偶数量）几乎和目标没有相关性。

此外不同特征之间的相关性也值得关注，如果有两个特征之间的相关性特别高（本例中没有，最高为票价和船舱等价-0.54），这说明这两个特征基本在描述同一个事情，可以考虑删去来降低维度。在线性回归的模型中，如果两个不同的变量相关性特别高，可能会导致系数估计不稳定、方差增大、解释性差。

共线性检查

python 复制代码

# 分离特征和标签（如果尚未分离）
X = df.drop('Survived', axis=1)
y = df['Survived']

# 计算方差膨胀因子 (VIF)
from statsmodels.stats.outliers_influence import variance_inflation_factor

vif_data = pd.DataFrame()
vif_data["feature"] = X.columns
vif_data["VIF"] = [variance_inflation_factor(X.values, i) for i in range(len(X.columns))]

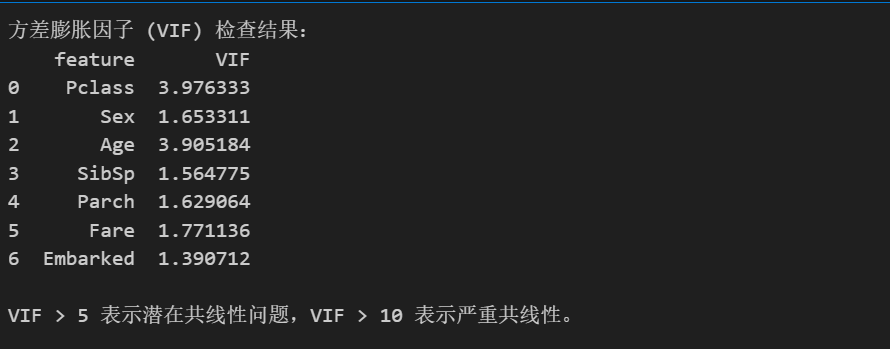
print("方差膨胀因子 (VIF) 检查结果：")
print(vif_data)
print("\nVIF > 5 表示潜在共线性问题，VIF > 10 表示严重共线性。")

分布分析

通过密度图/直方图检查特征分布是否偏斜，指导是否需要变换（如对数变换）。

通过Q-Q 图评估是否符合正态分布，影响统计检验选择。（许多经典检验依赖正态性假设，如果数据非正态（如 Age、Fare 等），这些检验可能无效，导致错误结论。所以对于非正态数据，使用非参数方法以确保结果可靠。或者使用不依赖正态分布的模型。

python 复制代码

# 密度图查看特征分布
import seaborn as sns
import matplotlib.pyplot as plt

numerical_features = ['Age', 'Fare', 'SibSp', 'Parch']

plt.figure(figsize=(12, 8))
for i, feature in enumerate(numerical_features, 1):
    plt.subplot(2, 2, i)
    sns.kdeplot(data=df, x=feature, fill=True)
    plt.title(f'{feature} 密度分布')
plt.tight_layout()
plt.show()

# 检查偏斜度
print("特征偏斜度 (Skewness)：")
for feature in numerical_features:
    skew = df[feature].skew()
    if abs(skew) > 1:
        print(f"{feature}: {skew:.2f} (高度偏斜)")
    else:
        print(f"{feature}: {skew:.2f} (绝对值 ≤ 1 表示偏斜较小)")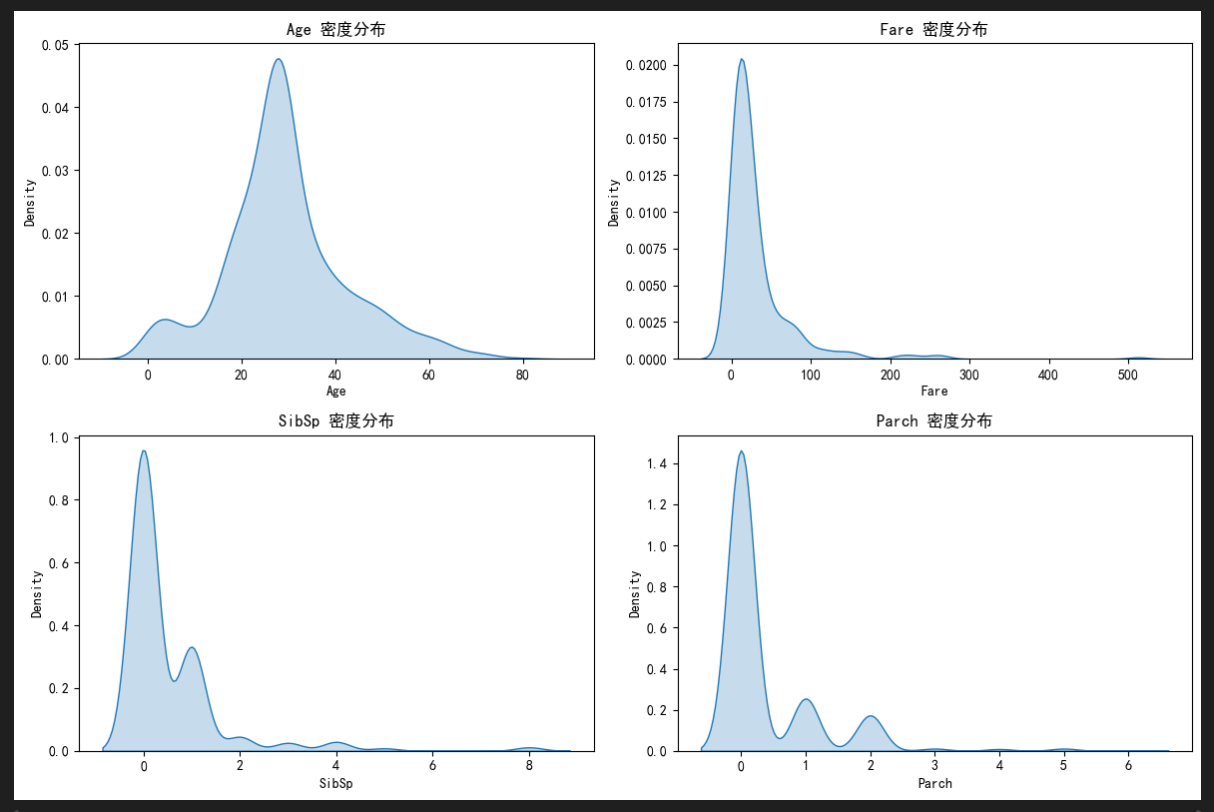

可以看到数值特征中有三个都分布偏斜

python 复制代码

# 正态性检验 (Shapiro-Wilk)
import scipy.stats as stats

print("正态性检验 (Shapiro-Wilk)：")
for feature in numerical_features:
    stat, p = stats.shapiro(df[feature].dropna())
    print(f"{feature}: p-value = {p:.4f} (p < 0.05 表示非正态)")

也可以发现，所有的数值特征都不符合正态分布。

事实上，相关性矩阵所用的Pearson系数也是依赖于正态分布的，但是其并不严格要求正态分布，因此得出的结论仍然有效，只不过相关性可能会偏低，这也就解释了为什么票价和船舱明明应该是强相关，但计算出的相关性只有-0.55左右。

分类特征分析

python 复制代码

# 分类特征与目标关联分析
categorical_features = ['Pclass', 'Sex', 'Embarked']

for feature in categorical_features:
    print(f"\n{feature} 与 Survived 的交叉表：")
    crosstab = pd.crosstab(df[feature], df['Survived'], normalize='index')
    print(crosstab)
    
    # 卡方检验
    from scipy.stats import chi2_contingency
    chi2, p, dof, expected = chi2_contingency(pd.crosstab(df[feature], df['Survived']))
    print(f"卡方检验: chi2 = {chi2:.2f}, p-value = {p:.4f} (p < 0.05 表示显著关联)")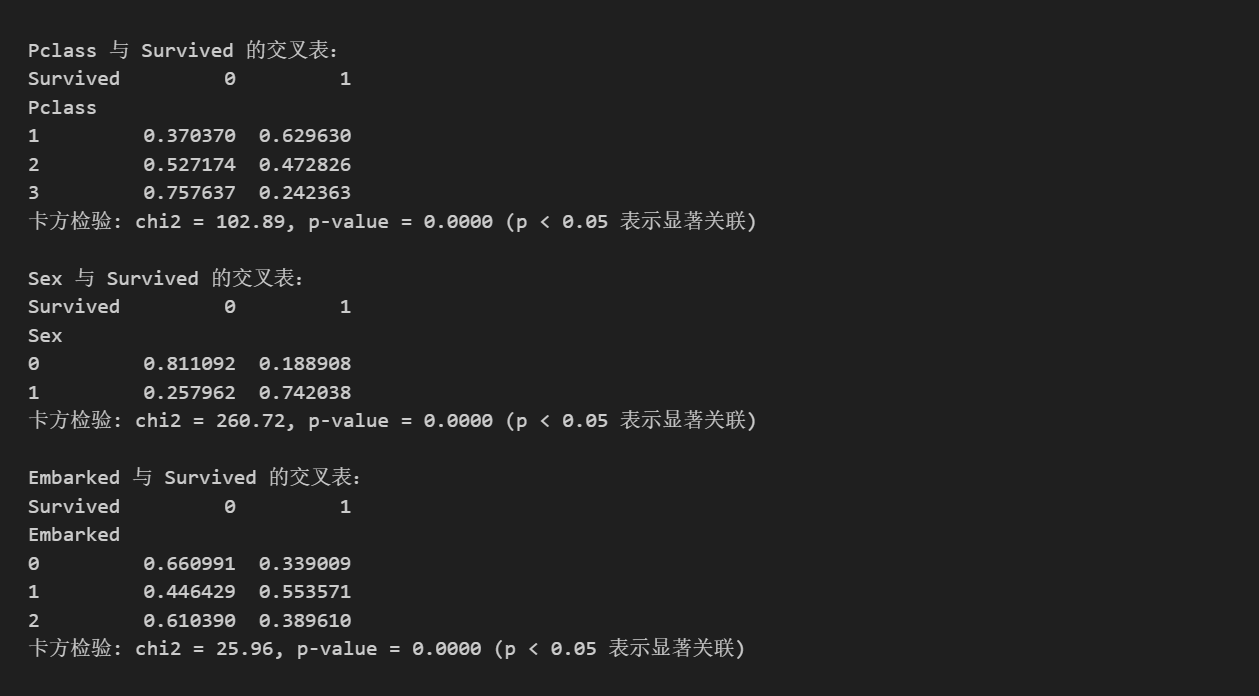

关键发现

Pclass：1等舱存活率 63%，2等舱 47%，3等舱 24%。卡方检验显著 (p=0.0000)，舱位等级对存活影响极大。
Sex：女性存活率 74%，男性 19%。显著关联 (p=0.0000)，性别是强预测因子。
Embarked：C港存活率 55%，Q港 39%，S港 34%。显著关联 (p=0.0000)，登船港口有影响。

至此，我们对所有特征的初步分析就已经结束了，由于该问题比较简单，探索多特征组合的价值比较有限（例如家庭规模 = SibSp + Parch）。后面尝试以此进行预测，如果效果不理想，再进行进一步的特征探索。

从项目入手机器学习——（四）特征工程（简单特征探索）

数据预处理

特征探索

数值特征

分类特征

数值特征分析

特征相关性矩阵

共线性检查

相关性矩阵与共线性的区别

分布分析

分类特征分析