海浪PM谱及波形的Matlab仿真实现

一、PM谱理论基础

Pierson-Moskowitz（PM）谱是描述完全发展海浪能量分布的经典模型，其核心公式为：

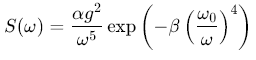
参数说明 ：
- ω0=gUω_0=\frac{g}{U}ω0=Ug：谱峰频率（UUU为海面19.5m高度风速）
- α=0.0081，β=0.74α=0.0081，β=0.74α=0.0081，β=0.74：经验常数
- g=9.81m/s2g=9.81 m/s^2g=9.81m/s2：重力加速度

二、Matlab仿真实现步骤

1. 参数设置与频谱计算

matlab 复制代码

% 物理参数设置
U = 12;          % 风速 (m/s)
g = 9.81;        % 重力加速度
alpha = 0.0081;  % PM谱参数
beta = 0.74;     % PM谱参数

% 频率参数
omega_0 = g / U; % 谱峰频率
omega_min = 0.2 * omega_0; % 最低频率
omega_max = 3.0 * omega_0; % 最高频率
N = 512;         % 频率分量数量
omega = linspace(omega_min, omega_max, N)'; % 频率向量
d_omega = omega(2) - omega(1); % 频率步长

% 计算PM谱
S_omega = (alpha * g^2) ./ (omega.^5) .* exp(-beta * (omega_0 ./ omega).^4);

2. 波数与相位生成

matlab 复制代码

% 波数计算（深水色散关系）
k = omega.^2 / g;

% 随机相位生成
rng('default'); % 固定随机种子
phi = 2 * pi * rand(N, 1); % [0, 2π)均匀分布相位

3. 波形叠加与仿真

matlab 复制代码

% 空间网格设置
Lx = 1000; % 海面长度 (m)
Ly = 1000; % 海面宽度 (m)
Nx = 256;  % x方向网格数
Ny = 256;  % y方向网格数
x = linspace(0, Lx, Nx);
y = linspace(0, Ly, Ny);
[X, Y] = meshgrid(x, y);

% 初始化波面高度矩阵
eta = zeros(Ny, Nx);

% 频率-方向离散化（二维扩展）
kx = 2*pi*(0:Nx-1)/Lx;
ky = 2*pi*(0:Ny-1)/Ly;
[KX, KY] = meshgrid(kx, ky);
K = sqrt(KX.^2 + KY.^2); % 波数模
theta = atan2(KY, KX);    % 波向角

% 二维PM谱计算
S_2D = S_omega' .* (1 + cos(theta)).^2; % 方向扩展因子（简化模型）

% 生成复振幅
A = sqrt(2 * S_2D * d_omega) .* exp(1i * phi);

% 二维傅里叶逆变换生成波面
eta = real(ifft2(ifftshift(A)));

4. 可视化

matlab 复制代码

% 固定位置时间序列（需扩展时间维度）
t = 0:0.1:100; % 时间向量
eta_t = zeros(length(t), Nx, Ny);
for ti = 1:length(t)
    eta_t(ti, :, :) = real(ifft2(ifftshift(A .* exp(1i * omega * t(ti)))));
end

% 动态3D显示
figure;
for ti = 1:100
    surf(X, Y, eta_t(ti, :, :), 'EdgeColor', 'none');
    shading interp;
    colormap(jet);
    view(45, 30);
    axis tight;
    title(sprintf('Time = %.1f s', t(ti)));
    drawnow;
end

三、关键参数与优化

1. 参数影响分析

参数	调整范围	效果影响
风速 UUU	5-20 m/s	波高↑、谱峰频率↓
频率范围	ωmin−ωmaxω_{min}-ω_{max}ωmin−ωmax	能量分布范围控制
网格分辨率	Nx×NyN_x×N_yNx×Ny	波面细节精度（建议≥256×256）

2. 算法优化技巧

快速傅里叶变换（FFT） ：利用fftshift和ifftshift优化计算效率
并行计算 ：对大规模网格（如1024×1024）使用parfor加速
内存管理 ：预分配数组避免动态扩展（如zeros初始化）

四、扩展模型与改进

1. 方向谱扩展

引入方向扩展因子D(θ)，构建三维PM谱：

S3D(ω,θ)=SPM(ω)⋅D(θ)S_3D(ω,θ)=S_{PM}(ω)⋅D(θ)S3D(ω,θ)=SPM(ω)⋅D(θ)

方向分布函数：常用cos²θ或(1+cosθ)²形式
代码修改：在二维傅里叶变换中增加方向权重

2. 非线性修正

Boussinesq方程：模拟浅水波非线性效应
高阶谱方法：引入二阶、三阶相互作用项

3. 实时交互仿真

matlab 复制代码

% 使用App Designer创建交互界面
app = uifigure;
slider = uislider(app, 'Position', [20 20 200 5], 'ValueChangedFcn', @(src,event) update_plot(src.Value));

五、结果验证与分析

1. 谱特性验证

matlab 复制代码

% 计算模拟谱
[pxx, f] = pwelch(eta(:), hamming(1024), 512, 1024, 1);

% 对比理论PM谱
figure;
semilogy(f, 10*log10(pxx), 'b', 'LineWidth', 1.5);
hold on;
plot(omega, 10*log10(S_omega), 'r--', 'LineWidth', 1.5);
xlabel('频率 (Hz)');
ylabel('功率谱密度 (dB/Hz)');
legend('实测谱', '理论PM谱');

2. 统计指标计算

有义波高 ：H1/3=4m0H_{1/3}=4\sqrt{m_0}H1/3=4m0 （m0m_0m0为谱零阶矩）
平均周期 ：Tm=ω02πT_m=\frac{ω0}{2π}Tm=2πω0

六、工程应用案例

船舶运动仿真：结合PM谱生成波浪载荷
海洋平台设计：分析波浪能分布对结构的影响
遥感图像处理：模拟SAR图像中的海浪调制效应

参考代码海浪PM谱及波形的matlab仿真 www.youwenfan.com/contentcsq/53438.html

注：实际应用中需根据具体场景调整参数，建议通过surf/mesh函数进行多角度可视化，并结合统计指标验证模型准确性。