载波相位同步
在数字通信系统中,解调器的输出需要按照符号周期进行定时采样才能正确恢复传输信息。由于发射机到接收机的传播延迟通常是未知的,接收端必须从接收信号中提取符号定时信息以实现同步采样。此外,传播延迟还会引起载波偏移,若使用相干检测器,接收端还需对该偏移进行估计。本章将重点讨论接收端实现载波同步和符号同步的具体方法。
信号参数估计
首先建立接收机输入端信号的数学模型。假设信道会对传输信号产生延迟并叠加高斯噪声干扰,则接收信号可表示为:
r ( t ) = s ( t − τ ) + n ( t ) r(t) = s(t - τ) + n(t) r(t)=s(t−τ)+n(t)
其中
s ( t ) = R e [ s l ( t ) e ( j 2 π f c t ) ] s(t) = Re[sₗ(t)e^{(j2πf_ct)}] s(t)=Re[sl(t)e(j2πfct)]
式中 τ τ τ表示传播时延, s l ( t ) sₗ(t) sl(t)为等效低通信号。
该接收信号还可表达为:
r ( t ) = R e { [ s l ( t − τ ) e ( j ϕ ) + z ( t ) ] e ( j 2 π f c t ) } r(t) = Re\left\{ [sₗ(t - τ)e^{(j\phi)} + z(t)] e^{(j2πf_ct)}\right\} r(t)=Re{[sl(t−τ)e(jϕ)+z(t)]e(j2πfct)}
其中载波相位 ϕ = − 2 π f c τ \phi = -2πf_cτ ϕ=−2πfcτ,由传播时延 τ τ τ决定。
表面看来,仅需估计传播时延 τ τ τ这一参数即可,因为已知 f c f_c fc和 τ τ τ就能确定 ϕ \phi ϕ。但实际情况更为复杂:
- 一方面,接收端解调载波振荡器与发射端存在不同步;
- 另一方面,二者振荡器可能随时间发生不同方向的缓慢漂移。
因此,接收载波相位并非仅由时延 τ τ τ决定。
此外,时间同步精度要求取决于符号间隔 T T T。时延 τ τ τ的估计误差通常需要控制在 T T T的较小比例范围内(如 ± 1 % T ±1\% T ±1%T)。但即便 ϕ \phi ϕ仅由 τ τ τ决定,该精度水平仍无法满足载波相位估计要求------由于 f c f_c fc通常很大, τ τ τ的微小误差会导致显著的相位偏差。
为了实现接收信号的解调和相干检测,需要同时对参数 τ \tau τ和 ϕ \phi ϕ进行估计。接收信号可表示为:
r ( t ) = s ( t ; ϕ , τ ) + n ( t ) r(t) = s(t; \phi, \tau) + n(t) r(t)=s(t;ϕ,τ)+n(t)
其中 ϕ \phi ϕ和 τ \tau τ为待估信号参数。为简化表达,将参数向量 { ϕ , τ } \left\{\phi, \tau\right\} {ϕ,τ}统一记为 θ \textbf{θ} θ,因此 s ( t ; ϕ , τ ) s(t; \phi, \tau) s(t;ϕ,τ)可简写为 s ( t ; θ ) s(t; \textbf{θ}) s(t;θ)。
信号参数估计主要基于两种准则:
- 最大似然(ML)准则 :将 θ \textbf{θ} θ视为确定但未知的参数
- 最大后验概率(MAP)准则 :将 θ \textbf{θ} θ建模为具有先验概率密度 p ( θ ) p(\textbf{θ}) p(θ)的随机变量
通过对 r ( t ) r(t) r(t)进行 N N N维正交展开,可用系数向量 r = ( r 1 , r 2 , . . . , r N ) r=(r₁, r₂, ..., r_N) r=(r1,r2,...,rN)表示接收信号。基于展开后的联合概率密度 p ( r ∣ θ ) p(r|\textbf{θ}) p(r∣θ):
- ML估计 :使 p ( r ∣ θ ) p(r|\textbf{θ}) p(r∣θ)最大化的 θ \textbf{θ} θ值
- MAP估计 :使后验概率 p ( θ ∣ r ) p(\textbf{θ}|r) p(θ∣r)最大化的 θ \textbf{θ} θ值
p ( θ ∣ r ) = p ( r ∣ θ ) p ( θ ) p ( r ) p(\textbf{θ}|r)=\frac{p(r|\textbf{θ})p(\textbf{θ})}{p(r)} p(θ∣r)=p(r)p(r∣θ)p(θ)
当参数向量 θ \textbf{θ} θ的先验分布未知时,可假设 p ( θ ) p(\textbf{θ}) p(θ)在参数取值范围内服从均匀分布(即常数)。此时,使 p ( r ∣ θ ) p(r|\textbf{θ}) p(r∣θ)最大化的 θ \textbf{θ} θ值同样会使 p ( θ ∣ r ) p(\textbf{θ}|r) p(θ∣r)最大化,因此最大后验估计(MAP)与最大似然估计(ML)将得到相同结果。
在讨论的参数估计方法中,将 θ \textbf{θ} θ和 r r r视为未知但确定的量,故采用最大似然准则进行估计。进行信号参数的ML估计时,要求接收机在大于信号周期 T T T的观测时长 T 0 T₀ T0(称为观测区间)内,通过接收信号观测来提取估计值。基于单次观测区间获得的估计值称为单次估计。实际应用中,通常采用(模拟或数字)跟踪环路进行连续估计,通过不断更新估计值来实现。单次估计不仅为跟踪环路的实现提供重要参考,其性能分析也有助于评估ML估计的表现,并与跟踪环路的结果建立关联。
似然函数
虽然可以通过展开 r ( t ) r(t) r(t)获得的随机变量 ( r 1 r 2 ⋅ ⋅ ⋅ r N ) (r₁ r₂ ··· r_N) (r1r2⋅⋅⋅rN)联合概率密度函数来推导参数估计值,但在估计信号波形参数时,直接处理信号波形更为便捷。因此,我们将建立一个连续时间等效模型来实现 p ( r ∣ θ ) p(r|\textbf{θ}) p(r∣θ)的最大化。
由于加性噪声 n ( t ) n(t) n(t)是白噪声且服从零均值高斯分布,联合概率密度函数 p ( r ∣ θ ) p(r|\textbf{θ}) p(r∣θ)可表示为:
p ( r ∣ θ ) = ( 1 2 π σ ) N e x p { − ∑ n = 1 N [ r n − s n ( θ ) ] 2 2 σ 2 } p(r|\textbf{θ})=(\frac{1}{\sqrt{2\pi}\sigma})^Nexp\left\{ -\sum \limits_{n=1}{N}\frac{[r_n-s_n(\textbf{θ})]^2}{2\sigma^2} \right\} p(r∣θ)=(2π σ1)Nexp{−n=1∑N2σ2[rn−sn(θ)]2}
r n = ∫ T 0 r ( t ) ϕ n ( t ) d t r_n=\int_{T_0}r(t)\phi_n(t)dt rn=∫T0r(t)ϕn(t)dt
s n = ∫ T 0 s ( t ; θ ) ϕ n ( t ) d t s_n=\int_{T_0}s(t;\textbf{θ})\phi_n(t)dt sn=∫T0s(t;θ)ϕn(t)dt
其中, T 0 T_0 T0 表示 r ( t ) r(t) r(t)和 s ( t ; θ ) s(t;\textbf{θ}) s(t;θ) 展开中的积分区间。 通过将上式方程代入,指数中的参数可以用信号波形 r ( t ) r(t) r(t)和 s ( t ; θ ) s(t;\textbf{θ}) s(t;θ) 来表示。
即:
lim N → ∞ 1 2 σ 2 ∑ n = 1 N [ r n − s n ( θ ) ] 2 = 1 N 0 ∫ T 0 [ r ( t ) − s ( t ; θ ) ] 2 d t \lim_{N \to \infty} \frac{1}{2\sigma^2 }\sum_{n=1}^{N}[r_n-s_n(\mathbf{\theta} )]^2= \frac{1}{N_0}\int_{T_0} [r(t)-s(t;\mathbf{\theta} )]^2dt limN→∞2σ21∑n=1N[rn−sn(θ)]2=N01∫T0[r(t)−s(t;θ)]2dt
现在,关于信号参数 θ \textbf{θ} θ使 p ( r ∣ θ ) p(r|\textbf{θ}) p(r∣θ)最大化的问题,等价于使似然函数
Λ ( θ ) = e x p { − 1 N 0 ∫ T 0 [ r ( t ) − s ( t ; θ ) ] 2 d t } Λ(\textbf{θ})=exp\left\{ -\frac{1}{N_0}\int_{T_0} [r(t)-s(t;\mathbf{\theta} )]^2dt \right\} Λ(θ)=exp{−N01∫T0[r(t)−s(t;θ)]2dt}
最大化的问题。接下来,我们将从最大化 Λ ( θ ) Λ(\textbf{θ}) Λ(θ)的角度来考虑信号参数估计。
载波相位估计
在接收端处理载波同步通常有两种基本方法。
第一种方法是采用频分复用方式传输一个特殊信号------导频信号,使接收机能够提取该信号,从而将其本地振荡器同步到接收信号的载波频率和相位上。当未调制的载波分量与承载信息的信号一同传输时,接收机使用锁相环(PLL)来捕获并跟踪该载波分量。锁相环被设计为窄带宽,因此基本不受信息信号频率分量的影响。
第二种方法在实践中更为普遍,即直接从调制信号中估计载波相位。这种方法具有显著优势:发射机功率可全部用于传输信息信号。在讨论载波恢复时,聚焦于第二种方法,因此假设信号通过抑制载波方式传输。
为强调准确相位估计的重要性,我们以双边带抑制载波(DSB/SC)信号的解调为例,分析载波相位误差的影响。具体而言,设幅度调制信号形式为
s ( t ) = A ( t ) c o s ( 2 π f c t + ϕ ) s(t) = A(t) cos(2πf_c t + \phi) s(t)=A(t)cos(2πfct+ϕ)
若用载波参考信号
c ( t ) = c o s ( 2 π f c t + ϕ ^ ) c(t) = cos(2πf_c t + \hat \phi) c(t)=cos(2πfct+ϕ^)
对信号进行解调,将得到
c ( t ) s ( t ) = 1 2 A ( t ) c o s ( ϕ − ϕ ^ ) + 1 2 A ( t ) c o s ( 4 π f c t + ϕ + ϕ ^ ) c(t)s(t) =\frac{1}{2}A(t) cos(\phi - \hat \phi) + \frac{1}{2}A(t) cos(4πf_c t + \phi + \hat \phi) c(t)s(t)=21A(t)cos(ϕ−ϕ^)+21A(t)cos(4πfct+ϕ+ϕ^)
通过低通滤波器滤除乘积信号 c ( t ) s ( t c(t)s(t c(t)s(t)中的双频分量后,可得到承载信息的信号:
y ( t ) = 1 2 A ( t ) c o s ( ϕ − ϕ ^ ) y(t) =\frac{1}{2}A(t)cos(\phi-\hat \phi) y(t)=21A(t)cos(ϕ−ϕ^)
需注意相位误差 ϕ − ϕ ^ \phi-\hat \phi ϕ−ϕ^会导致信号电压幅度衰减 c o s ( ϕ − ϕ ^ ) cos(\phi-\hat \phi) cos(ϕ−ϕ^)倍,功率衰减 c o s 2 ( ϕ − ϕ ^ ) cos²(\phi-\hat \phi) cos2(ϕ−ϕ^)倍。
因此对于调幅信号,10°相位误差将产生0.13分贝的功率损耗,30°相位误差则导致1.25分贝损耗。
正交幅度调制(QAM)和多相相移键控(M-PSK)中载波相位误差的影响更为严重。这类信号可表示为:
s ( t ) = A ( t ) c o s ( 2 π f c t + ϕ ) − B ( t ) s i n ( 2 π f c t + ϕ ) s(t) = A(t)cos(2πf_ct+\phi) - B(t)sin(2πf_ct+\phi) s(t)=A(t)cos(2πfct+ϕ)−B(t)sin(2πfct+ϕ)
解调时采用两个正交载波:
c i ( t ) = c o s ( 2 π f c t + ϕ ) c_i(t) = cos(2πf_ct+\phi) ci(t)=cos(2πfct+ϕ)
c q ( t ) = − s i n ( 2 π f c t + ϕ ) c_q(t) = -sin(2πf_ct+\phi) cq(t)=−sin(2πfct+ϕ)
将 s ( t ) s(t) s(t)与 c i ( t ) c_i(t) ci(t)相乘并经低通滤波后,可得**同相分量**:
y I ( t ) = 1 2 A ( t ) c o s ( ϕ − ϕ ^ ) − 1 2 B ( t ) s i n ( ϕ − ϕ ^ ) y_I(t) =\frac{1}{2}A(t)cos(\phi-\hat \phi) - \frac{1}{2}B(t)sin(\phi-\hat \phi) yI(t)=21A(t)cos(ϕ−ϕ^)−21B(t)sin(ϕ−ϕ^)
同理, s ( t ) s(t) s(t)与 c q ( t ) c_q(t) cq(t)相乘滤波后得到**正交分量**:
y Q ( t ) = 1 2 B ( t ) c o s ( ϕ − ϕ ^ ) + 1 2 A ( t ) s i n ( ϕ − ϕ ^ ) y_Q(t) =\frac{1}{2}B(t)cos(\phi-\hat \phi) + \frac{1}{2}A(t)sin(\phi-\hat \phi) yQ(t)=21B(t)cos(ϕ−ϕ^)+21A(t)sin(ϕ−ϕ^)
上式明确表明:相较于脉幅调制(PAM)信号解调,QAM和M-PSK信号解调中的相位误差影响更为严重。不仅会导致期望信号功率按 c o s 2 ( ϕ − ϕ ^ ) cos²(\phi-\hat \phi) cos2(ϕ−ϕ^)比例衰减,还会引起同相与正交分量间的串扰。由于 A ( t ) A(t) A(t)和 B ( t ) B(t) B(t)的平均功率水平相近,微小相位误差就会造成性能显著劣化。因此QAM和多相相干PSK对相位精度的要求远高于双边带抑制载波PAM(DSB/SC PAM)。
ML载波相位估计
首先,推导最大似然载波相位估计。为简化起见,假设时延 τ \tau τ已知且特别设 τ = 0 \tau=0 τ=0。将0代入 θ \textbf{θ} θ后,该函数变为:
Λ ( ϕ ) = e x p { − 1 N 0 ∫ T 0 [ r t − s ( t ; ϕ ) ] 2 d t } = e x p { − 1 N 0 ∫ T 0 r 2 ( t ) d t + 2 N 0 ∫ T 0 r ( t ) s ( t ; ϕ ) d t − 1 N 0 ∫ T 0 s 2 ( t ; ϕ ) d t } Λ(\mathbf{\phi})=exp\left\{ -\frac{1}{N_0}\int_{T_0} [r_t-s(t;\phi)]^2dt \right\} =exp\left\{ -\frac{1}{N_0}\int_{T0}r^2(t)dt+\frac{2}{N_0}\int_{T_0}r(t)s(t;\phi)dt-\frac{1}{N_0}\int_{T_0}s^2(t;\phi)dt \right\} Λ(ϕ)=exp{−N01∫T0[rt−s(t;ϕ)]2dt}=exp{−N01∫T0r2(t)dt+N02∫T0r(t)s(t;ϕ)dt−N01∫T0s2(t;ϕ)dt}
请注意,指数因子的第一项不涉及信号参数 ϕ \phi ϕ。 第三项包含 s 2 ( t ; ϕ ) s²(t;\phi) s2(t;ϕ)的积分,对于任何 ϕ \phi ϕ值都是一个常数,等于观测区间 T 0 T₀ T0内的信号能量。 只有第二项涉及接收信号 r ( t ) r(t) r(t)与信号 s ( t ; ϕ ) s(t;\phi) s(t;ϕ)的互相关,其值取决于 ϕ \phi ϕ的选择。 因此,似然函数 Λ ( ϕ ) Λ(\phi) Λ(ϕ)可表示为:
Λ ( θ ) = C ⋅ exp [ ( 2 / N 0 ) ∫ T 0 r ( t ) s ( t ; ϕ ) d t ] Λ(θ) = C\cdot \text{exp}[(2/N₀)∫_{T_0}r(t)s(t;\phi) dt] Λ(θ)=C⋅exp[(2/N0)∫T0r(t)s(t;ϕ)dt]
其中 C C C是与 ϕ \phi ϕ无关的常数。
最大似然估计 ϕ ^ M L \hat \phi_{ML} ϕ^ML是使上式中 Λ ( ϕ ) Λ(\phi) Λ(ϕ)最大化的θ值。 等价地, ϕ ^ M L \hat \phi_{ML} ϕ^ML也最大化 Λ ( ϕ ) Λ(\phi) Λ(ϕ)的对数,即对数似然函数:
Λ L ( θ ) = ( 2 / N 0 ) ∫ T 0 r ( t ) s ( t ; θ ) d t Λ_L(θ) = (2/N₀)∫_{T_0}r(t)s(t;θ) dt ΛL(θ)=(2/N0)∫T0r(t)s(t;θ)dt
需注意在定义 Λ L ( ϕ ) Λ_L(\phi) ΛL(ϕ)时,我们忽略了常数项 ln C \text{ln} C lnC。
PLL
锁相环(PLL)基本由乘法器 、环路滤波器 和 压控振荡器(VCO) 组成,如下图所示。
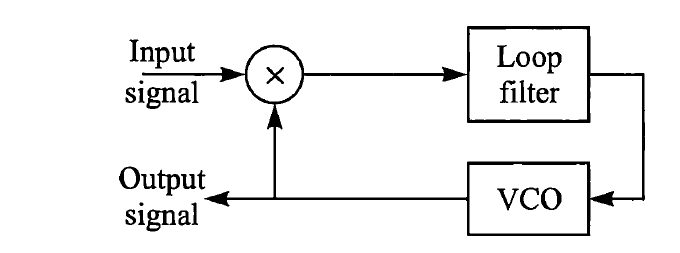
假设锁相环的输入是正弦波 c o s ( 2 π f c t + ϕ ) cos(2πf_ct + \phi) cos(2πfct+ϕ),VCO的输出为 s i n ( 2 π f c t + ϕ ^ ) sin(2πf_ct + \hat\phi) sin(2πfct+ϕ^),其中 ϕ ^ \hat\phi ϕ^表示对 ϕ \phi ϕ的估计值,则这两个信号的乘积为:
e ( t ) = c o s ( 2 π f c t + ϕ ) s i n ( 2 π f c t + ϕ ^ ) = ( 1 / 2 ) s i n ( ϕ ^ − ϕ ) + ( 1 / 2 ) s i n ( 4 π f c t + ϕ + ϕ ^ ) e(t) = cos(2πf_ct + \phi) sin(2πf_ct + \hat\phi) = (1/2)sin( \hat\phi - \phi) + (1/2)sin(4πf_ct + \phi + \hat\phi) e(t)=cos(2πfct+ϕ)sin(2πfct+ϕ^)=(1/2)sin(ϕ^−ϕ)+(1/2)sin(4πfct+ϕ+ϕ^)
环路滤波器是一个低通滤波器,仅对低频分量 ( 1 / 2 ) s i n ( ϕ ^ − ϕ ) (1/2)sin(\hat\phi - \phi) (1/2)sin(ϕ^−ϕ)产生响应,并滤除 2 f c 2f_c 2fc处的分量。该滤波器通常选择具有相对简单的传递函数。
G ( s ) = 1 + τ 2 s 1 + τ 1 s G(s)=\frac{1+\tau_2s}{1+\tau_1s} G(s)=1+τ1s1+τ2s
其中 τ 1 \tau_1 τ1和 τ 2 \tau_2 τ2是控制环路带宽的设计参数( τ 1 > τ 2 \tau_1 > \tau_2 τ1>τ2)。如需获得更好的环路响应,可采用含附加极点的更高阶滤波器。环路滤波器输出为压控振荡器(VCO)提供控制电压 v ( t ) v(t) v(t)。该VCO本质上是一个正弦信号发生器,其瞬时相位表达式为:
2 π f c t + ϕ ^ ( t ) = 2 π f c t + K ∫ − ∞ t v ( τ ) d τ 2πf_ct + \hat\phi(t)=2πf_ct +K\int_{-\infty}^{t}v(\tau)d\tau 2πfct+ϕ^(t)=2πfct+K∫−∞tv(τ)dτ
其中 K K K是以弧度/伏为单位的增益常数。因此,
ϕ ^ ( t ) = K ∫ − ∞ t v ( τ ) d τ \hat\phi(t)=K\int_{-\infty}^{t}v(\tau)d\tau ϕ^(t)=K∫−∞tv(τ)dτ