文章目录
01背包
理论
01背包问题是一个经典的动态规划问题,旨在不超过 背包容量的前提下,选择物品使得总价值最大。每个物品只能选或不选(0或1)。
问题描述
- 输入:
n个物品,每个物品有重量w[i]和价值v[i],背包容量W。 - 输出:能放入背包的最大价值。
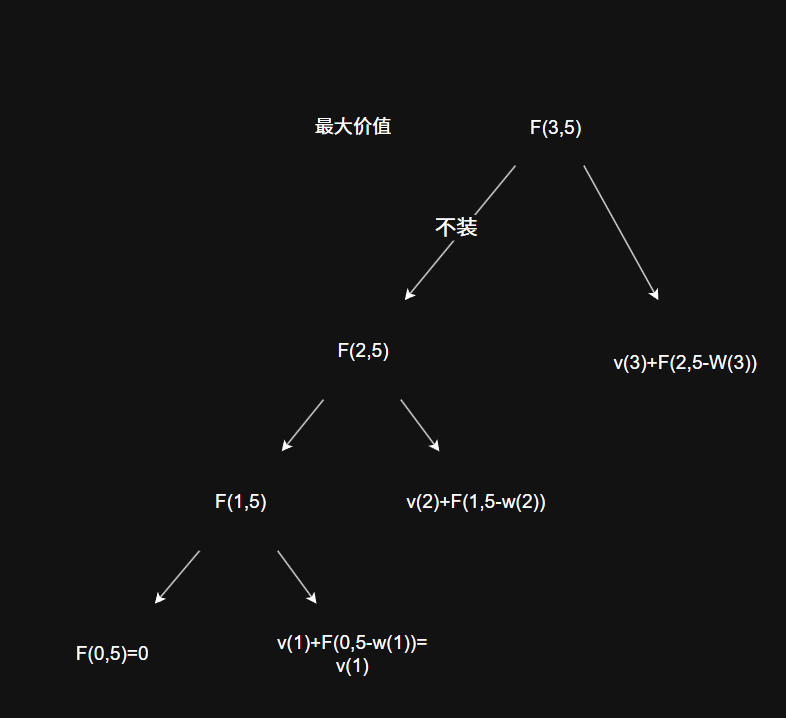
F(n.C)考虑将n个物品放入容量为C的背包里的价值,使得价值最大**F(i,C)=max{不装入i,装入i}**
F(i,C) =max{F(i-1, C),v(i)+F(i-1,C-w(i))}
依次考虑放不放,
- 递归和记忆化搜索表
- 自底向上动态规划(如表格)
n为背包有几个元素以及对第几个元素操作完了
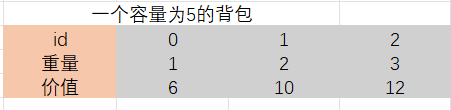
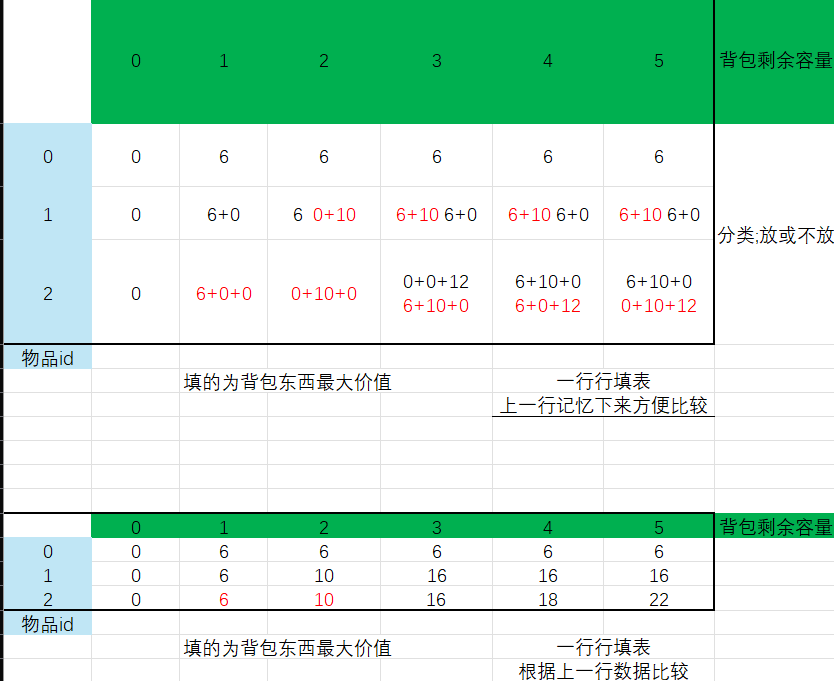
动态规划表
递归+记忆化搜索+动态规划方法代码
c
#include<stdio.h>
#include<stdlib.h>
int weight[] = { 1,2,3 };
int value[] = { 6,10,12 };
int capacity = 5;
static int maxx(int a, int b) {
return a > b ? a : b;
}
//index 当前处理物品 [0,n-1]
//c背包剩余容量
static int bestValue01(int index, int c) {
if (index < 0 || c <= 0) {
return 0;
}
//1.不放 物品index
int res=bestValue01(index - 1, c);
//2.放 物品index
//放进去之前保证能装下
if (weight[index] <= c) {
//比较 装进去与否价值
//假设已经处理完了bestValue01(index-1,c-weight[index])
//这个是 处理物品index前 的最大价值
res = maxx(res, value[index] + bestValue01(index - 1, c - weight[index]));
}
return res;
}
//法一:递归
int knapsack01() {
int n = sizeof(weight) / sizeof(weight[0]);
return bestValue01(n-1,capacity);
}
//index 当前处理物品
//c 剩余容量
//mem 记录表
// index物品操作后最大价值
static int bestValue02(int index, int c, int** mem) {
if (index < 0 || c <= 0) {
return 0;
}
//0.如果已经处理过
if (mem[index][c] != -1) {
return mem[index][c];
}
//1.不放 物品index
int res = bestValue01(index - 1, c);
//2.放 物品index
//放进去之前保证能装下
if (weight[index] <= c) {
//比较 装进去与否价值
//假设已经处理完了bestValue01(index-1,c-weight[index])
//这个是 处理物品index前 的最大价值
res = maxx(res, value[index] + bestValue01(index - 1, c - weight[index]));
}
//3.记录当前结果
mem[index][c] = res;
return res;
}
//法二:记忆化搜索 自顶向下的动态规划
int knapsack02() {
//3行(物品个数)6列背包剩余容量可能(0--5)
int n = sizeof(weight) / sizeof(weight[0]);
int** mem = malloc(n * sizeof(int*));
if (mem == NULL)return -1;
for (int i = 0; i < n; i++)
{
mem[i] = malloc(sizeof(int) * (capacity + 1));
if (mem[i] == NULL)return -1;
}
for (int i = 0; i < n; i++)
{
for (int j = 0; j <= capacity; j++)
{
mem[i][j] = -1;
}
}
return bestValue02(n - 1, capacity, mem);
}
//法三:自底向上的动态规划
int knapsack03DP() {
//1.创建dp数组
//里面填为最大价值 两个变量 物品的index和背包剩余容量
int n = sizeof(value) / sizeof(value[0]);
int** dp = malloc(sizeof(int*) * n);
if (dp == NULL)return -1;
for (int i = 0; i < n; i++)
{
dp[i] = malloc(sizeof(int*) * (capacity+1));
if (dp[i] == NULL)return -1;
}
//1.5 初始化第一行 处理第一个物品
for (int i = 0; i <= capacity ; i++)//遍布背包剩余容量
{
//放得下与否 决定了是空还是有物品能放进去
dp[0][i] = (weight[0] <= i) ? value[0] : 0;
}
//2.填表(一行行)
for (int i = 1; i < n; i++)
{
for (int j = 0; j <= capacity; j++)
{
//dp[i - 1][j] 不放物品i, 等于之前状态
//value[i] + dp[i - 1][j - weight[i]]放进去了就等于
//当前物品的价值加上 操作前一个物品后最大价值=操作后的最大价值
// index=i-1 c=j - weight[i]的前提下(前一个物品后最大价值)
dp[i][j] = maxx(dp[i - 1][j], value[i] + dp[i - 1][j - weight[i]]);
}
}
return dp[n-1][capacity];
}
int main() {
//int res = knapsack01();
//int res = knapsack02();
int res = knapsack03DP();
printf("result:%d", res);
return 0;
}