labview最小二乘法拟合曲线报表生成,波形拟合最小二乘法 LabVIEW是一种流程图编程语言和开发环境,用于控制和测量系统的自动化。最小二乘法是一种数学优化技术,用于拟合数据点到一个函数曲线上。在LabVIEW中,可以使用最小二乘法来生成报表和进行波形拟合。 最小二乘法是一种通过最小化数据点与拟合曲线之间的误差平方和来确定最佳拟合曲线的方法。它适用于各种领域,包括统计学、工程学和物理学等。通过使用最小二乘法,可以找到最适合数据的曲线,并用于预测、分析和优化。 LabVIEW提供了一种直观的方式来实现最小二乘法拟合曲线和生成报表。通过使用LabVIEW的图形化编程环境,您可以构建一个拟合模型,将数据点输入到模型中,并使用最小二乘法算法来计算最佳拟合曲线的参数。然后,您可以使用LabVIEW的报表生成功能,将拟合结果以表格或图形的形式呈现出来。 LabVIEW还提供了丰富的波形处理和分析工具,可以帮助您进行波形拟合。通过使用LabVIEW的信号处理模块,您可以对波形数据进行预处理,例如滤波、降噪和采样。然后,您可以使用最小二乘法来拟合波形数据,并生成拟合曲线的报表。 总之,LabVIEW是一种强大的工具,可用于实现最小二乘法拟合曲线和生成报表。它结合了图形化编程和数学优化技术,使得数据分析和处理变得更加直观和高效。无论是在科学研究、工程设计还是数据分析领域,LabVIEW都是一个非常有用的工具。
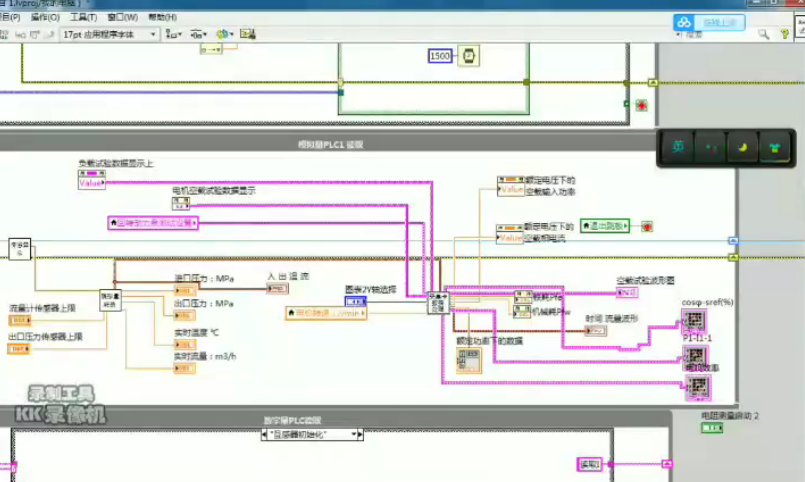
在自动化控制和测量系统的开发领域,LabVIEW凭借其独特的流程图编程方式和强大功能脱颖而出。而最小二乘法,作为数学优化技术里的一颗璀璨明珠,在拟合数据点到函数曲线方面发挥着关键作用。今天咱们就来唠唠在LabVIEW里,如何借助最小二乘法实现曲线拟合以及报表生成,还有波形拟合的那些事儿。
最小二乘法:数据拟合的核心秘籍
最小二乘法,简单来说,就是通过最小化数据点与拟合曲线之间误差平方和,来确定那条最适合数据的曲线。就好比给一群散点找一个最合适的"家"(曲线),让它们尽可能都"住得舒服"(误差最小)。这个方法在统计学、工程学、物理学等众多领域都有广泛应用,从预测未来趋势到优化系统性能,它都能大显身手。
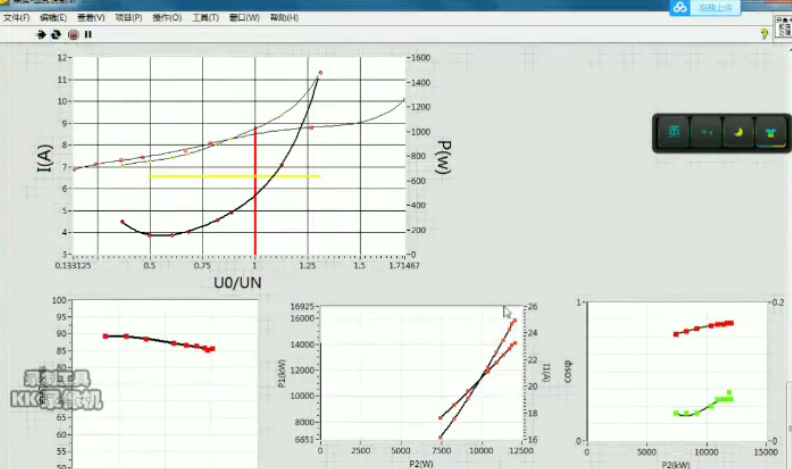
labview最小二乘法拟合曲线报表生成,波形拟合最小二乘法 LabVIEW是一种流程图编程语言和开发环境,用于控制和测量系统的自动化。最小二乘法是一种数学优化技术,用于拟合数据点到一个函数曲线上。在LabVIEW中,可以使用最小二乘法来生成报表和进行波形拟合。 最小二乘法是一种通过最小化数据点与拟合曲线之间的误差平方和来确定最佳拟合曲线的方法。它适用于各种领域,包括统计学、工程学和物理学等。通过使用最小二乘法,可以找到最适合数据的曲线,并用于预测、分析和优化。 LabVIEW提供了一种直观的方式来实现最小二乘法拟合曲线和生成报表。通过使用LabVIEW的图形化编程环境,您可以构建一个拟合模型,将数据点输入到模型中,并使用最小二乘法算法来计算最佳拟合曲线的参数。然后,您可以使用LabVIEW的报表生成功能,将拟合结果以表格或图形的形式呈现出来。 LabVIEW还提供了丰富的波形处理和分析工具,可以帮助您进行波形拟合。通过使用LabVIEW的信号处理模块,您可以对波形数据进行预处理,例如滤波、降噪和采样。然后,您可以使用最小二乘法来拟合波形数据,并生成拟合曲线的报表。 总之,LabVIEW是一种强大的工具,可用于实现最小二乘法拟合曲线和生成报表。它结合了图形化编程和数学优化技术,使得数据分析和处理变得更加直观和高效。无论是在科学研究、工程设计还是数据分析领域,LabVIEW都是一个非常有用的工具。
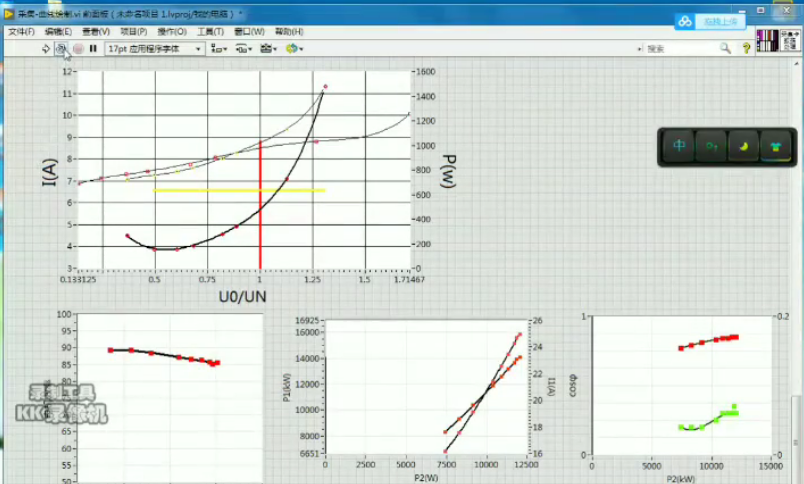
想象一下,我们有一堆实验测量得到的数据点,要找到一条曲线能最好地反映这些数据的变化规律。最小二乘法就派上用场啦。数学公式这里就不赘述了,咱们直接看LabVIEW里怎么实现。
LabVIEW实现最小二乘法拟合曲线
在LabVIEW的图形化编程环境里,构建拟合模型就像搭积木一样直观。下面咱们来看一段简单代码示例(这里为示意,并非完整可运行代码):
-
数据输入部分 :
- 首先我们得有数据点对吧。假设我们有一组横坐标数组
x和纵坐标数组y,这可以通过各种方式获取,比如从文件读取或者硬件采集。 - 在LabVIEW里,我们可以使用"数组常量"来创建简单的测试数据数组。例如:
labview
// 创建横坐标数组
x = [1, 2, 3, 4, 5];
// 创建纵坐标数组
y = [2, 4, 6, 8, 10];
这里简单创建了两个数组来模拟数据,实际应用中数据获取方式会复杂得多。
- 首先我们得有数据点对吧。假设我们有一组横坐标数组
-
最小二乘法拟合模块 :
- LabVIEW里有专门的函数来实现最小二乘法拟合。比如"曲线拟合"函数,我们把刚才创建的
x和y数组连接到这个函数的对应输入端口。 - 这个函数会根据最小二乘法算法计算出最佳拟合曲线的参数,比如对于线性拟合,它会给出直线的斜率和截距。
- 代码示意:
labview
// 假设使用曲线拟合函数,输入x和y数组
FitResult = CurveFit(x, y);
// FitResult中包含拟合曲线的参数,如斜率Slope和截距Intercept
Slope = FitResult.Slope;
Intercept = FitResult.Intercept;
这里
CurveFit函数是示意性的,实际LabVIEW中有对应的具体函数节点。通过这个函数,我们就得到了拟合曲线的关键参数。 - LabVIEW里有专门的函数来实现最小二乘法拟合。比如"曲线拟合"函数,我们把刚才创建的
-
绘制拟合曲线 :
- 得到参数后,我们就可以绘制拟合曲线了。LabVIEW里有绘图相关的函数,比如"波形图表"。
- 我们根据得到的斜率和截距,生成一系列新的点来绘制曲线。代码大概如下:
labview
// 创建用于绘制曲线的新横坐标数组,假设范围与原x相同
newx = [1, 2, 3, 4, 5];
newy = [];
for (i = 0; i < newx.length; i++) {
// 根据斜率和截距计算新纵坐标
newy[i] = Slope * newx[i] + Intercept;
}
// 将newx和newy连接到波形图表进行绘制
PlotWaveform(newx, new_y);
这样我们就把拟合曲线绘制出来了,能直观看到数据点和拟合曲线的关系。
报表生成:让结果一目了然
拟合完曲线,我们还得把结果以合适的形式呈现出来,这就用到LabVIEW的报表生成功能啦。LabVIEW可以把拟合结果以表格或者图形的形式生成报表。
-
表格报表 :
- 我们可以创建一个表格,把横坐标、纵坐标数据点以及拟合曲线对应的计算值都列进去。
- 在LabVIEW里,使用"报表生成工具包"里的相关函数。比如先创建一个表格对象:
labview
// 创建报表对象
Report = CreateReport();
// 添加表头
AddHeader(Report, "X", "Y", "Fitted Y");
for (i = 0; i < x.length; i++) {
// 计算拟合曲线上对应x点的y值
fittedy = Slope * x[i] + Intercept;
// 添加数据行
AddRow(Report, x[i], y[i], fittedy);
}
// 保存报表为文件
SaveReport(Report, "FitResultReport.xlsx");
这样就生成了一个包含数据点和拟合结果的表格报表,方便查看和分析。
-
图形报表 :
- 除了表格,我们还可以生成包含拟合曲线和数据点的图形报表。这时候可以结合前面绘制拟合曲线的部分,再加上一些注释和说明。
- 比如使用"图形绘制"函数,在图形上标注数据点、拟合曲线公式等信息。
labview
// 创建图形报表对象
GraphReport = CreateGraphReport();
// 绘制数据点
PlotPoints(GraphReport, x, y);
// 绘制拟合曲线
PlotCurve(GraphReport, newx, newy);
// 添加注释,比如拟合曲线公式
AddAnnotation(GraphReport, "Y = " + Slope + "X + " + Intercept);
// 保存图形报表为图片
SaveGraphReport(GraphReport, "FitResultGraph.png");
通过这样的图形报表,能更直观地展示拟合效果。
波形拟合:LabVIEW的又一利器
LabVIEW在波形处理和分析方面同样实力强劲。在进行波形拟合时,通常需要先对波形数据进行预处理。
- 波形预处理 :
-
比如滤波,去除噪声干扰。LabVIEW里有各种滤波器函数,像低通滤波器,可以通过设置截止频率等参数来过滤掉高频噪声。
labview
// 假设原始波形数据存储在waveform数组中
filteredwaveform = LowPassFilter(waveform, cutofffrequency); -
降噪和采样也是常见的预处理步骤。降噪可以使用均值滤波等方法,采样则可以根据需求调整波形数据的采样率。
-
-
波形最小二乘法拟合 :
- 经过预处理后,就可以使用最小二乘法对波形数据进行拟合了。和前面的曲线拟合类似,把处理后的波形数据作为输入,使用相应的拟合函数。
labview
// 假设处理后的波形横坐标为waveformx,纵坐标为filteredwaveform
WaveformFitResult = CurveFit(waveformx, filteredwaveform);
// 获取波形拟合曲线的参数
WaveformSlope = WaveformFitResult.Slope;
WaveformIntercept = WaveformFitResult.Intercept;
这样就得到了波形拟合曲线的参数,进而可以绘制波形拟合曲线并生成相关报表。
- 经过预处理后,就可以使用最小二乘法对波形数据进行拟合了。和前面的曲线拟合类似,把处理后的波形数据作为输入,使用相应的拟合函数。
总之,LabVIEW就像一个宝藏工具箱,把图形化编程和数学优化技术(如最小二乘法)完美结合。无论是科研人员分析实验数据,还是工程师设计系统,亦或是数据分析师处理大量数据,LabVIEW都能凭借其在最小二乘法拟合曲线和报表生成方面的强大功能,让数据分析和处理变得高效又直观。赶紧动手试试吧,说不定能在你的项目中发现更多惊喜!