SVM支持向量机:找一条"最宽的分隔线"
从"分蛋糕"看SVM的核心思想
想象你在给两个小朋友分蛋糕,蛋糕上有两种水果:草莓(红色)和蓝莓(蓝色)。你需要切一刀,把草莓和蓝莓完全分开。怎么切最公平?
普通切法:随便切一刀,只要分开就行。
SVM切法:找到一条"最宽的分隔线",让草莓和蓝莓到线的距离都尽可能远。这样即使蛋糕稍微晃动(数据有噪声),水果也不会跑到线的另一边。
这就是SVM(Support Vector Machine,支持向量机)的核心思想:不仅要分开不同类别,还要让分隔线的"安全距离"最大。
什么是"支持向量"?
在SVM中,离分隔线最近的那些点(草莓或蓝莓)被称为"支持向量"(Support Vectors)。它们是决定分隔线位置的关键------就像拔河比赛中最靠近中间线的那些人,是胜负的关键。
- 如果移动非支持向量的点,分隔线不会变;
- 但如果移动支持向量,分隔线就必须重新计算。
所以SVM只"关心"那些离分隔线最近的点,这让它在处理高维数据时非常高效。
SVM的"完美分隔三步法"
第1步:画一条初步的分隔线
假设我们有以下数据点(横轴x,纵轴y):
- 草莓(红色):(1, 2), (2, 3), (3, 1)
- 蓝莓(蓝色):(6, 5), (7, 7), (8, 6)
在坐标系上画一条直线,比如y = x - 1,看起来能把两类点分开。
第2步:计算"安全距离"(间隔)
SVM定义了两种距离:
- 点到线的距离:每个点到分隔线的垂直距离。
- 间隔(Margin):两类点到分隔线的最小距离之和(即"安全距离")。
以上面的直线为例:
- 最近的草莓点(2,3)到线的距离≈0.707
- 最近的蓝莓点(6,5)到线的距离≈1.414
- 间隔=0.707 + 1.414≈2.121
第3步:找到"最大间隔"的线
SVM的目标是找到使"间隔"最大的那条线。通过计算,最优分隔线可能是y = x - 3,此时:
- 最近的草莓点(3,1)到线的距离≈1.414
- 最近的蓝莓点(6,5)到线的距离≈1.414
- 间隔=1.414 + 1.414≈2.828(比之前的2.121更大)
这条线就是SVM找到的"最宽分隔线",它让两类点都有足够的安全距离。
当数据"歪歪扭扭"时:核函数的魔法
问题:线性不可分的数据
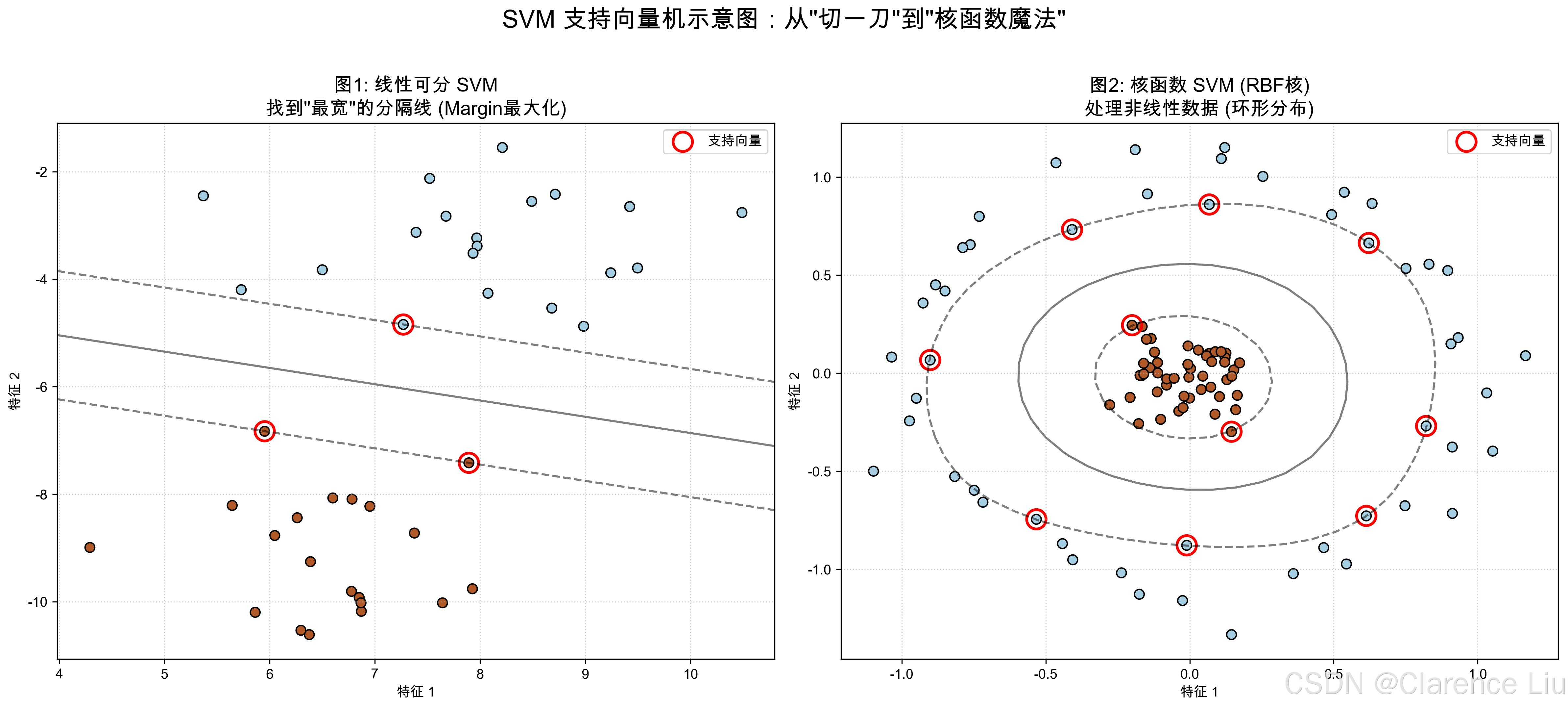
如果数据点是环形分布(比如红色点在里面,蓝色点在外面),用直线无论如何都分不开。这时候SVM的"核函数"就派上用场了。
核函数:把数据"掰弯"到高维空间
核函数的作用就像"把纸折起来":
- 在二维平面上环形分布的数据无法用直线分开;
- 但如果把纸折成三维,环形就变成了一个"碗",此时用一个平面就能把里外的点分开。
SVM常用的核函数有:
- 线性核:不做变换,适用于线性可分数据;
- 多项式核:通过x²、x³等项把数据升到高维;
- RBF核(径向基函数):最常用的核函数,能处理各种复杂分布(比如环形、螺旋形)。
可以简单理解为:核函数帮SVM在高维空间中找到分隔平面,再映射回低维空间,就变成了曲线 。
生活中的SVM:不止"分蛋糕"
案例1:垃圾邮件识别
- 特征:邮件中的关键词("免费""中奖""点击"等)构成的向量;
- SVM作用:找到最佳分隔线,区分垃圾邮件(正类)和正常邮件(负类);
- 优势:即使关键词很多(高维特征),SVM也能高效找到分隔线。
案例2:图像识别
- 特征:图像的像素值、边缘特征等;
- SVM作用:区分不同物体(如猫和狗);
- 优势:对噪声不敏感,小样本也能训练出好模型。
案例3:信用卡欺诈检测
- 特征:交易金额、时间、地点等;
- SVM作用:区分正常交易和欺诈交易;
- 优势:能处理高维特征,且对异常点(欺诈交易)敏感。
SVM vs 逻辑回归:各有所长
| 算法 | 核心思想 | 优势 | 劣势 |
|---|---|---|---|
| SVM | 最大化间隔,找到最优分隔线 | 对高维数据高效,小样本效果好 | 计算量大,不直接输出概率 |
| 逻辑回归 | 计算类别概率,阈值判断 | 输出概率,训练快 | 对复杂分布拟合能力弱 |
简单说:如果数据特征多、样本少,选SVM;如果需要概率输出、训练速度快,选逻辑回归。
SVM的"小脾气":调参是门艺术
脾气1:对噪声敏感
如果数据中有离群点(比如一个草莓混在蓝莓里),SVM可能会为了迁就它而把分隔线画歪。解决办法是"软间隔":允许少数点越过分隔线,只要整体间隔最大。
脾气2:核函数选择难
选线性核还是RBF核?这需要根据数据分布试错。一般先试线性核,效果不好再用RBF核。
脾气3:参数C的影响(惩罚系数)
在SVM中,参数C代表**"对错误的容忍度"**。它平衡了两个目标:
- 分得对:尽可能把所有样本分类正确。
- 分得宽:让分隔线的间隔(Margin)尽可能大。
-
当 C 值很大(严格模式) :
SVM会拼命想把每一个点都分对,甚至不惜把分隔线扭曲得很难看,或者让间隔变得很窄。
- 后果 :在训练集上表现完美,但遇到新数据容易出错(过拟合)。
- 类比:像一个有洁癖的老师,容不得学生犯一点错,导致学生只会死记硬背。
-
当 C 值很小(宽容模式) :
SVM允许一些点分错,或者允许一些点跑到间隔里(这就是"软间隔"),只要整体的分隔线足够宽、足够简单。
- 后果 :容错性强,泛化能力好,但如果太小可能会分错太多(欠拟合)。
- 类比:像一个抓大放小的老师,允许你偶尔粗心,只要掌握了核心解题思路就行。
数学上的解释(不想看公式可跳过) :
SVM的优化目标是最小化这个函数:
minw,b,ξ12∣∣w∣∣2+C∑i=1nξi \min_{w,b,\xi} \frac{1}{2}||w||^2 + C \sum_{i=1}^{n} \xi_i w,b,ξmin21∣∣w∣∣2+Ci=1∑nξi
这个公式包含两部分:
- 左边 12∣∣w∣∣2\frac{1}{2}||w||^221∣∣w∣∣2 :这部分越小,间隔(Margin)越大。它代表"简单、宽的分隔线"。
- 右边 C∑ξiC \sum \xi_iC∑ξi :这部分越小,分错的点越少(ξi\xi_iξi 是第 iii 个点的错误程度)。它代表"分类准确性"。
参数 C 就是这一天平上的砝码:C 越大,越重视右边的"准确性";C 越小,越重视左边的"宽间隔"。
调参秘籍:通常从C=1开始试,如果发现模型在训练集上错误率高,就增大C;如果模型在测试集上表现差(过拟合),就减小C。
小问题:为什么SVM在大数据时代不那么火了?
(提示:SVM的时间复杂度是O(n²),当数据量超过10万样本时,训练速度会很慢。而深度学习(如神经网络)在大数据上表现更好,所以SVM逐渐被用于小样本、高维特征的场景。)
下一篇预告:《深度学习:堆"多层神经网络"会发生什么?》------用"剥洋葱"的例子,讲透深度神经网络的工作原理。