图论是离散数学中用于建模事物之间连接关系的强大工具。它将问题抽象为由顶点 (Vertices) 和边 (Edges) 组成的网络。这个模型在社交网络分析、物流路径规划、互联网路由等领域有着广泛的应用。
以下是一个逐步构建和应用图论模型的示例。
1. 建立顶点:抽象出个体 (The Nodes)
首先,我们将现实世界中的个体或实体抽象为图中的"顶点"(或节点)。在下图中,我们有四个独立的顶点 A、B、C 和 D。这可以代表四个城市、四个人、或者四个网络服务器。

2. 建立边:定义关系 (The Edges)
接下来,我们用"边"来表示这些个体之间的关系。如果在两个顶点之间存在某种直接的联系,我们就用一条线将它们连接起来。
在下图中,我们建立了如下关系:A与B相连,B与C相连,C与D相连,D与A相连。这就形成了一个简单的环形图。这可以代表城市之间的直达航班,或者社交网络中的好友关系。
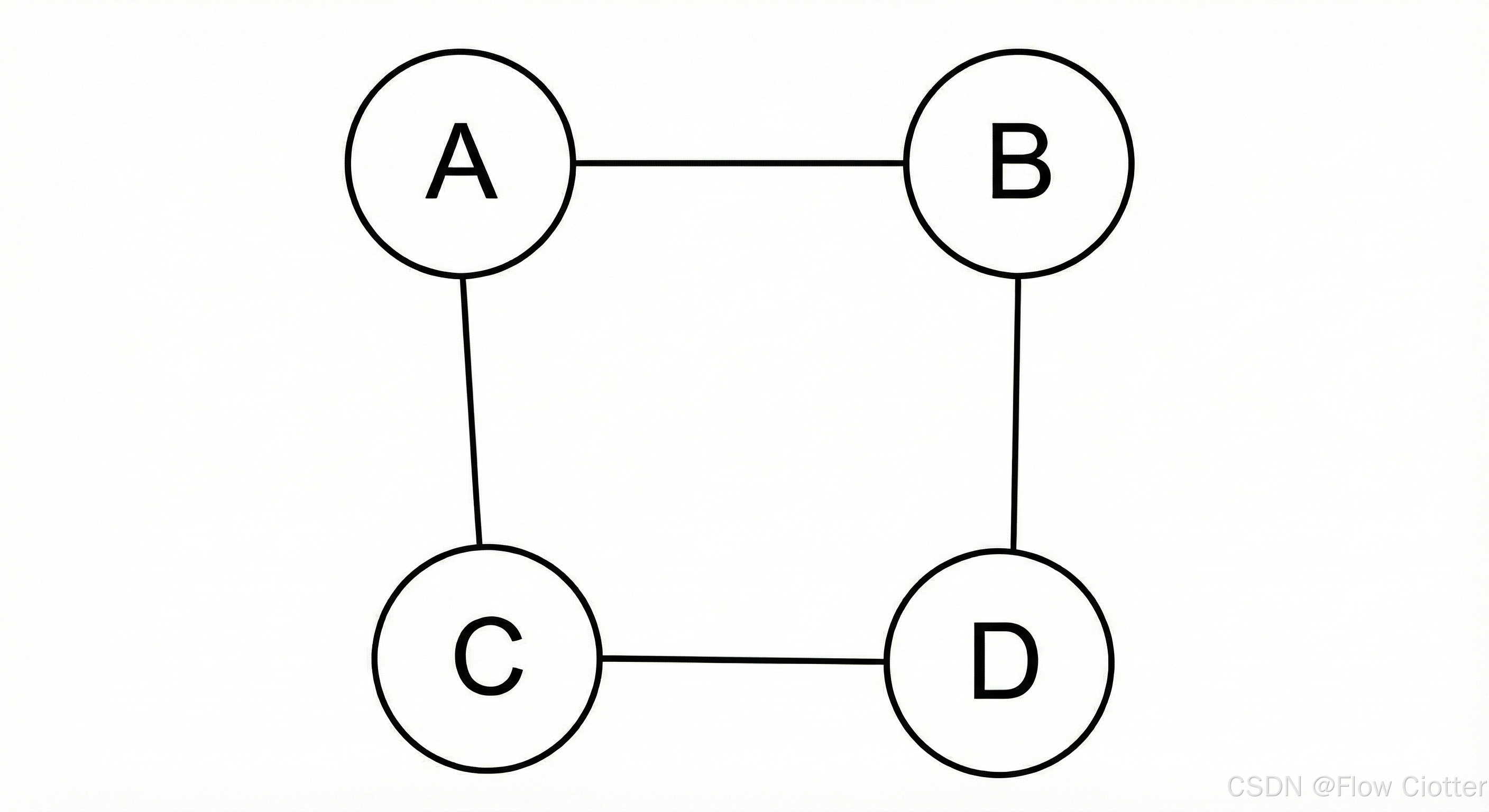
- 模型应用:寻找路径 (Finding a Path)
有了这个图论模型,我们就可以解决各种问题,比如寻找两个顶点之间的路径。
假设我们要找出从顶点 A 到顶点 C 的一条路径。通过观察图,我们可以找到一条路径:A -> B -> C。在下图中,我们将这条路径以及路径上的顶点用红色高亮显示出来。这演示了如何利用图论模型来解决实际的连接性问题。
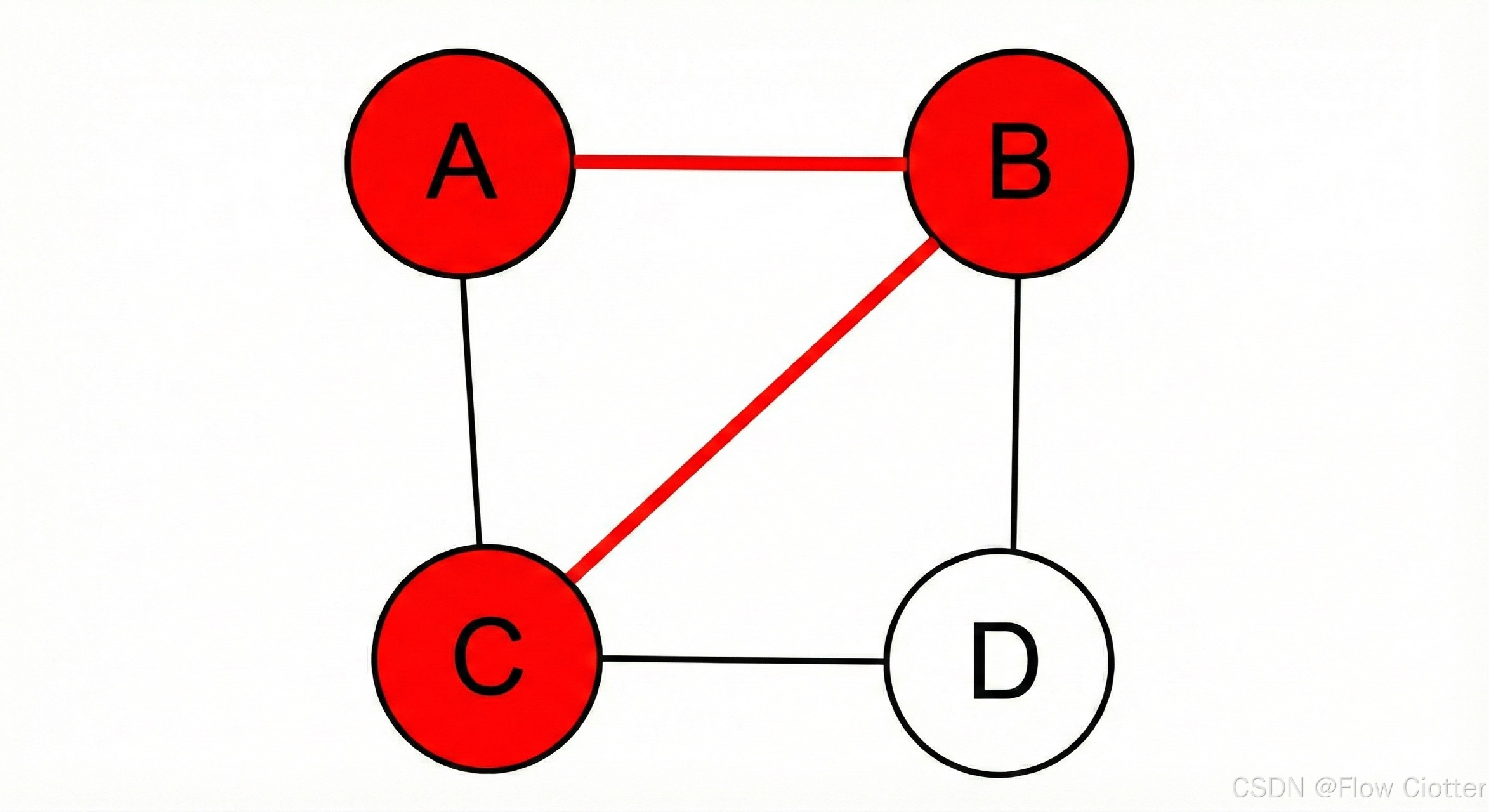
这就是一个典型的离散数学模型示例:通过建立图模型,将现实问题抽象为顶点和边,然后利用图论算法来寻找路径或解决连接性问题。