KMP模式搜索算法

KMP模式搜索算法

Knuth-Morris-Pratt（KMP）算法是一种高效的字符串匹配算法，用于在文本中寻找模式。它通过预处理步骤智能处理不匹配，实现线性时间复杂度。KMP由Donald Knuth、Vaughan Pratt和James Morris于1977年开发。它被广泛应用于搜索引擎、编译器和文本编辑器中。

目录

天真的方法以及KMP如何克服它

LPS（最长前缀后缀）阵列

构建LPS数组的算法

KMP模式匹配算法

现实应用

相关问题

天真的方法以及KMP如何克服它

在朴素字符串匹配算法中，我们在文本的每个位置对齐模式，并逐个比较字符。如果出现不匹配，我们会将模式移动一个位置并重新开始。这可能导致多次重复检查同一字符，尤其是在字符重复的情况下。例如，在"aaaaab"中搜索"aaaab"会导致许多不必要的比较，导致时间复杂度为O（n × m）。

KMP算法通过使用名为LPS（最长前缀后缀）的辅助数组预处理模式，避免了这种低效 。该数组存储最长的适当前缀长度，该前缀也是模式中每个前缀的后缀。当出现不匹配时，KMP会利用这些信息智能地调整模式，跳过那些注定不匹配的局面------而不是重新开始。这确保文本中的每个字符最多被比较一次，将时间复杂度降低到 O（n + m）。

真前缀：字符串的真前缀是指不等于字符串本身的前缀。

例如，"abcd"的专前缀有：""、"a"、"ab"和"abc"。

LPS（最长前缀后缀）阵列

LPS 数组对模式中的每个位置存储最长的适当前缀长度，该前缀也是该位置结束子串的后缀。

它帮助KMP算法在出现不匹配时确定模式的偏移幅度，而无需重新检查匹配的字符。

lps[] 构造示例：

示例1：模式"aabaaac"

索引0处："a" → 无合适的前缀/后缀 → lps[0] = 0

索引1时："aa" → "a" 既是前缀又后缀 → lps[1] = 1

索引2处："aab" → 没有前缀与 lps[2] = 0 → 后缀不匹配 pps[2] = 0

索引3时："aaba" → "a" 是前缀和后缀 → lps[3] = 1

索引4： "aabaa" → "aa" 是前缀和后缀 → lps[4] = 2

索引 5："aabaaa" → "aa" 是前缀和后缀 →lps[5] = 2

索引 6："aabaaac" → 不匹配，因此重置 → lps[6] = 0

最终 lps[]： [0， 1， 0， 1， 2， 2， 0]

示例2：模式"abcdabca"

索引0处：lps[0] = 0

索引1处：lps[1] = 0

索引2：lps[2] = 0

索引3处：lps[3] = 0（"abcd中无重复"）

索引4处：lps[4] = 1（"a"重复）

索引5处：lps[5] = 2（"ab"重复）

索引6处：lps[6] = 3（"abc"重复）

索引7处：lps[7] = 1（不匹配， 回归"a"）

最终LPS：[0， 0， 0， 0， 1， 2， 3， 1]

注：lps[i] 也可以定义为最长的前缀，这也是一个合适的后缀。我们需要在一个地方正确使用它，以确保整个子串都不被考虑。

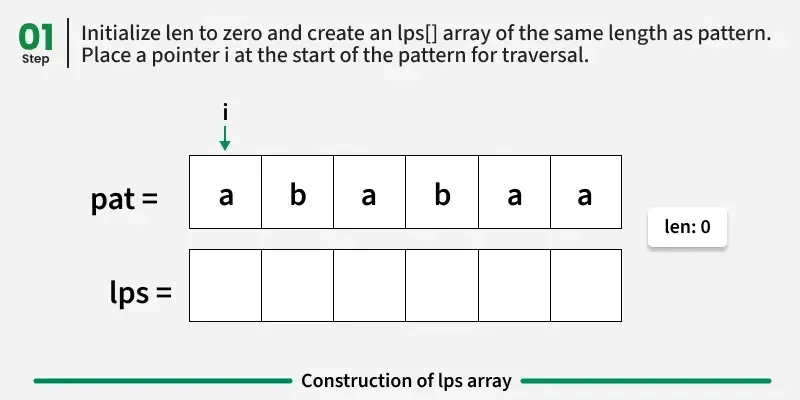
构建LPS数组的算法

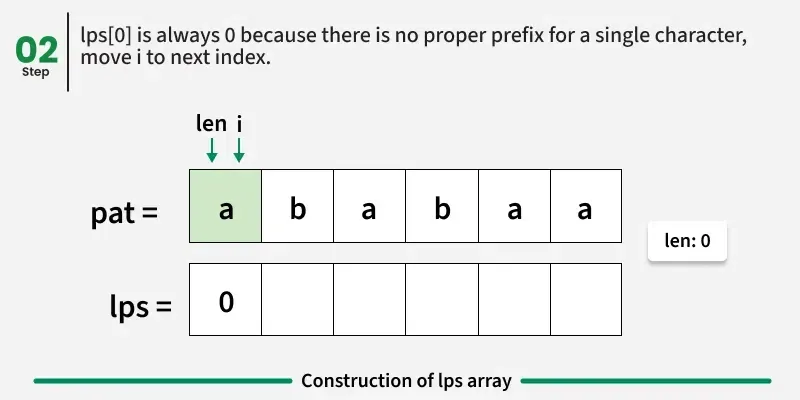
lps[0] 的值总是 0，因为长度为 1 的字符串没有非空的真前缀，且该前缀也是后缀。我们维护一个变量len，初始化为0，用来跟踪之前最长前缀后缀的长度。从索引1开始，我们对当前字符pat[i]与pat[len]进行比较。基于这种比较，我们有三种可能的情况：

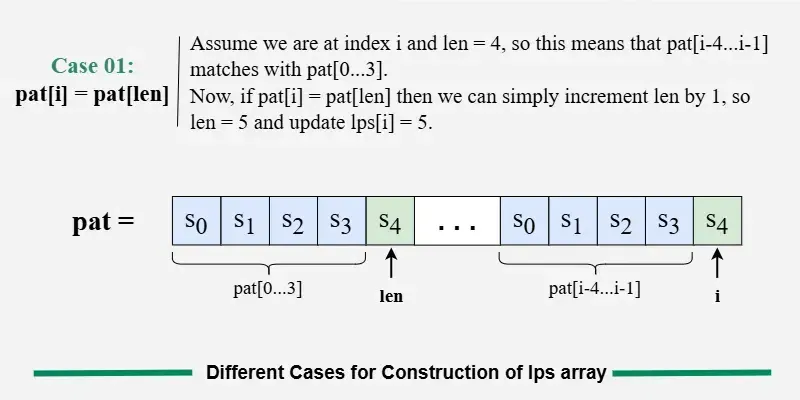
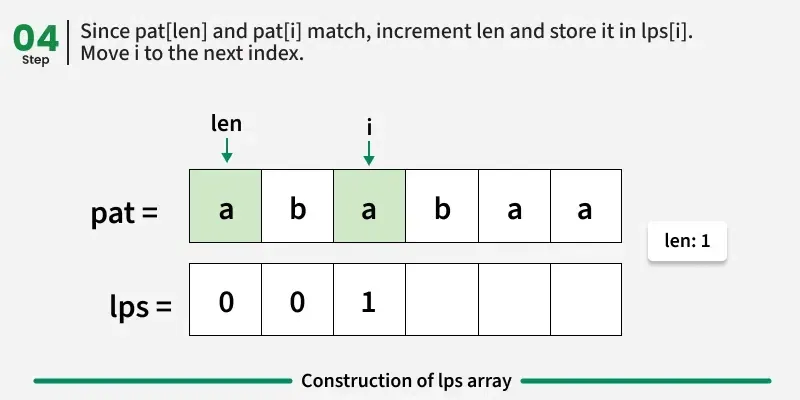
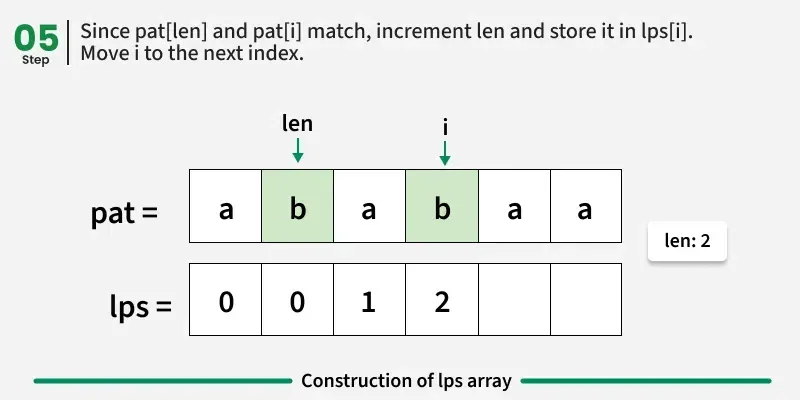
情况1：pat[i] == pat[len]

这意味着当前角色继续使用现有的前缀-后缀匹配。

→ 我们将 len 增加 1，并赋值 lps[i] = len。

→ 然后，进入下一个索引。

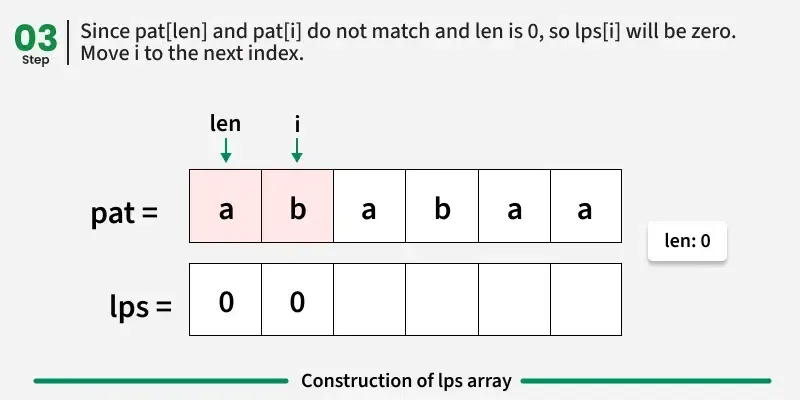
情况2：pat[i] ！= pat[len] 和 len == 0

没有任何前缀能匹配以 i 结尾的后缀，也无法退回到任何早期的匹配模式。

→ 我们设 lps[i] = 0，然后直接跳到下一个字符。

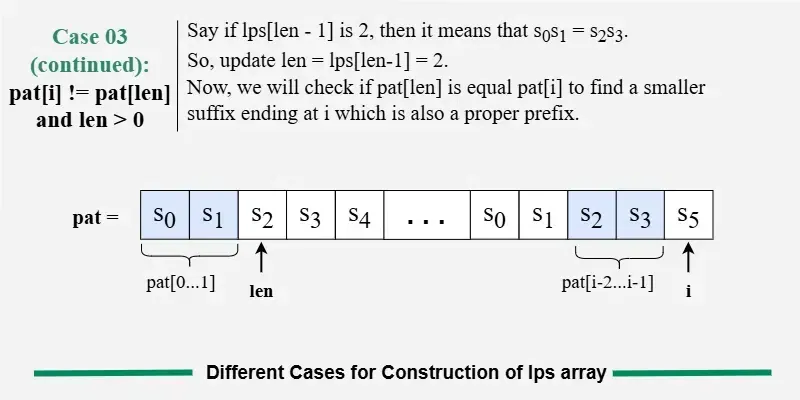
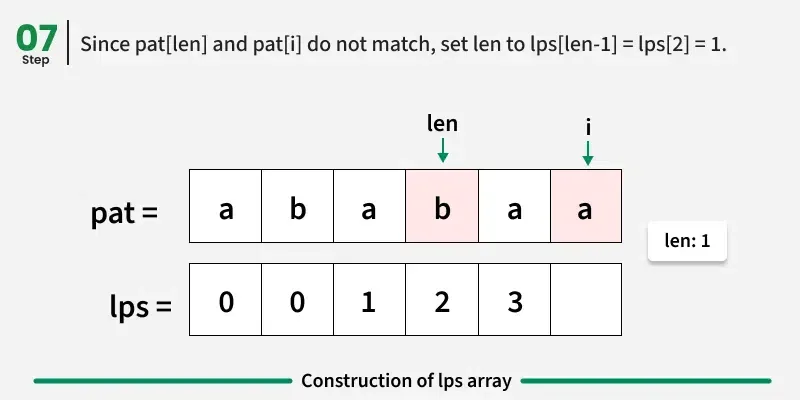
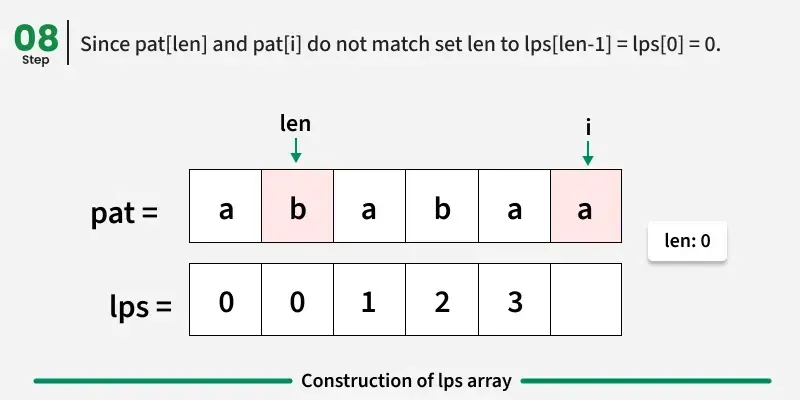
情况3：pat[i] ！= pat[len] 和 len > 0

我们无法扩展之前匹配的前缀后缀。不过，可能仍然会有一个更短的前缀，也是一个与当前位置相符的后缀。

我们不再手动比较所有前缀，而是重复使用之前计算的LPS值。

→ 由于 pat[0...len-1] 等于 pat[i-len...I-1]，我们可以退回LPS[len - 1]并更新Len。

→ 这样可以减少我们匹配的前缀大小，避免重复工作。

在这种情况下，我们不会立即增加 i------而是用更新后的 len 重新尝试当前的 pat[i]。

插图：

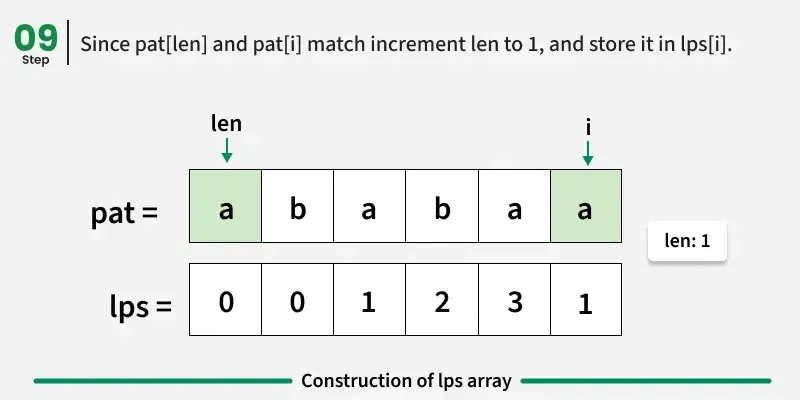
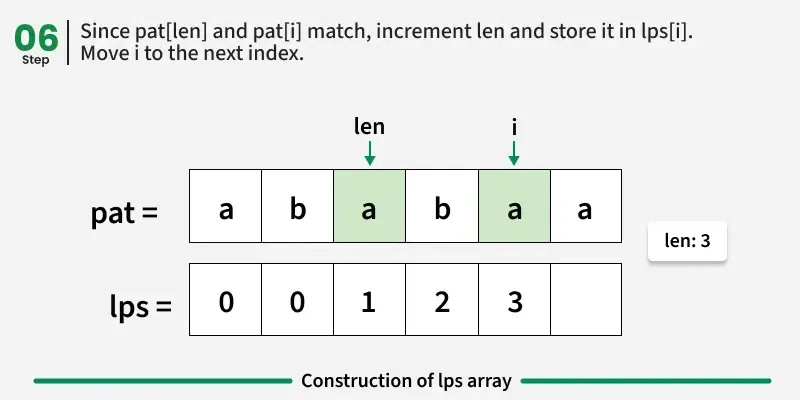
LPS阵列的构造示例：

class GfG {
    public static ArrayList<Integer> computeLPSArray(String pattern) {
        int n = pattern.length();
        ArrayList<Integer> lps = new ArrayList<>();
        for (int k = 0; k < n; k++) lps.add(0);

        // length of the previous longest prefix suffix
        int len = 0;
        int i = 1;

        while (i < n) {
            if (pattern.charAt(i) == pattern.charAt(len)) {
                len++;
                lps.set(i, len);
                i++;
            } else {
                if (len != 0) {
                    // fall back in the pattern
                    len = lps.get(len - 1);
                } else {
                    lps.set(i, 0);
                    i++;
                }
            }
        }

        return lps;
    }
}

时间复杂度：O（n），模式中的每个字符最多处理两次------一次在前进时（i++），可能在倒退时使用len = lps[len - 1]步骤处理一次。

辅助空间：O（n），一个大小等于图案的额外数组lps[]。

KMP模式匹配算法

KMP算法中使用的术语：

文本（txt）：我们想在其中搜索模式的主字符串。

pattern（pat）：我们试图在文本中找到的子字符串。

匹配：当模式中的所有字符都与文本的子串完全对齐时，发生匹配。

LPS 数组（最长前缀后缀）：对于模式中的每个位置 i，lps[i] 存储最长的真前缀长度，该前缀也是子串 pat[0...i] 中的后缀。

专前缀：真前缀是指不等于整串的前缀。

后缀：后缀是终止于当前位置的子字符串。

LPS阵列帮助我们确定在出现不匹配时可以跳跃多少模式，从而避免重复的比较。

问题陈述：

给定两个字符串：txt，代表主文，pat，表示要搜索的模式。

查找并返回txt中所有字符串pat作为子字符串出现的起始索引。

匹配应当精确，索引应为基于0，也就是说txt的第一个字符被视为索引0。

示例：

输入：txt = "abcab"，pat = "ab"

输出：[0， 3]

解释：字符串"ab"在txt中出现两次，第一次从索引0开始，第二次从索引3开始。

输入：txt = "aabaacaadaaba"，pat = "aaba"

输出：[0， 9， 12]

解释：

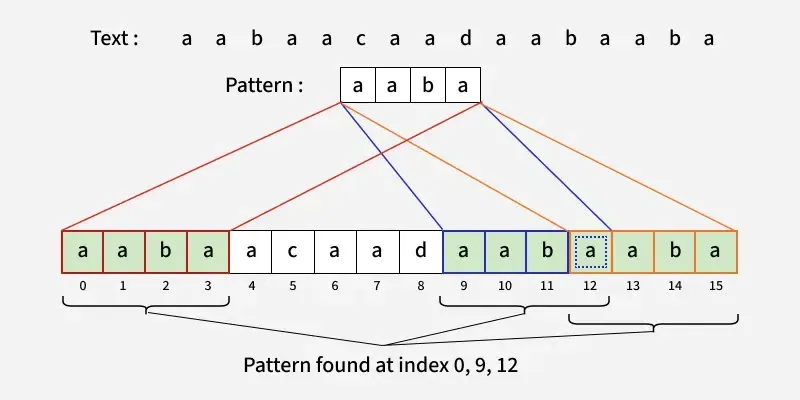
示例

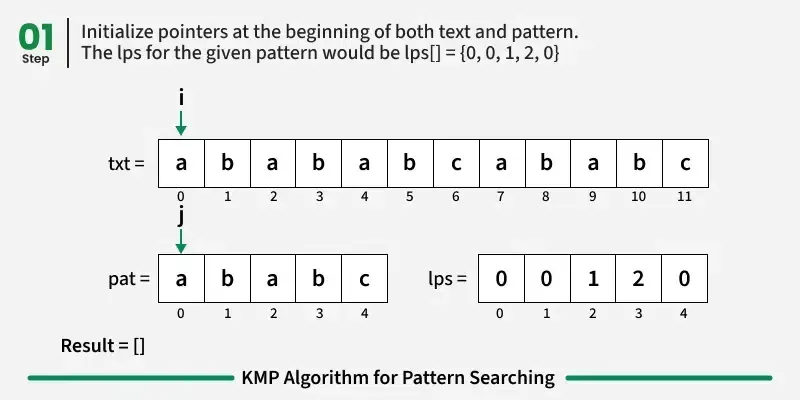
KMP算法主要分为两个步骤：

1. 预处理步骤------构建LPS阵列

首先，我们处理这个模式，创建一个称为LPS（最长前缀后缀）的数组。

这个数组告诉我们："如果此时出现不匹配，我们可以在模式中跳回多远而不错过任何潜在匹配？"

这有助于我们避免在不匹配后从图案的起点重新开始。

这一步只做一次，然后我们开始在文本中搜索。

2. 匹配步骤------在文本中搜索图案

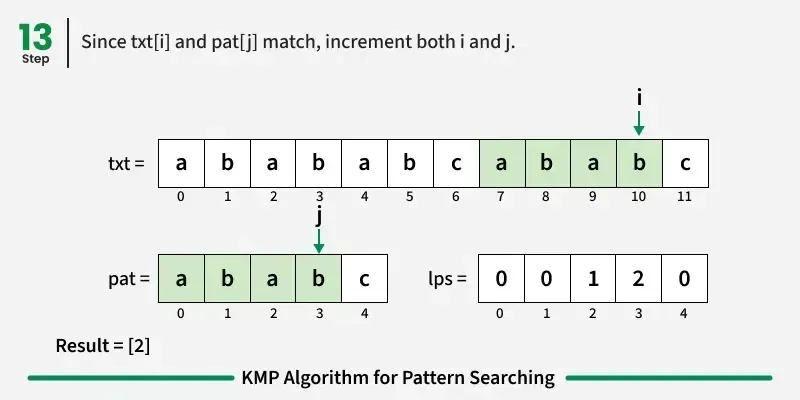
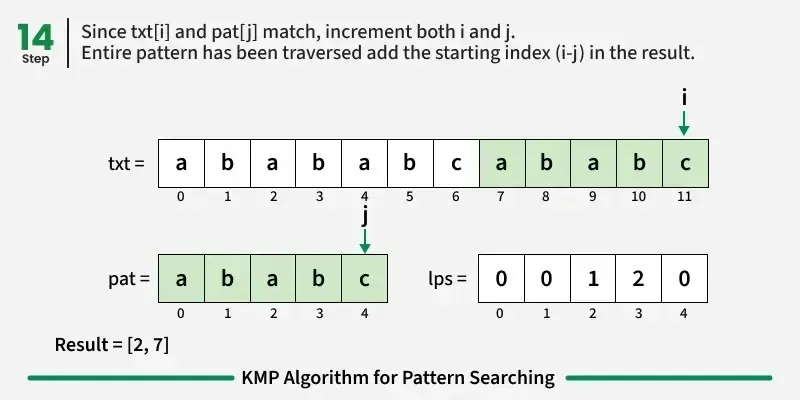
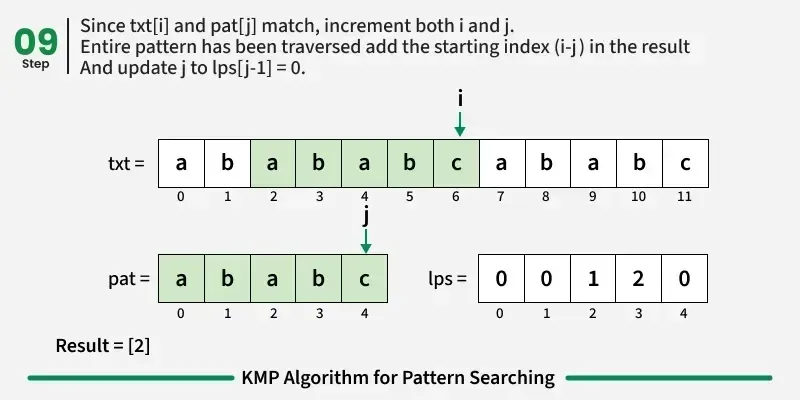
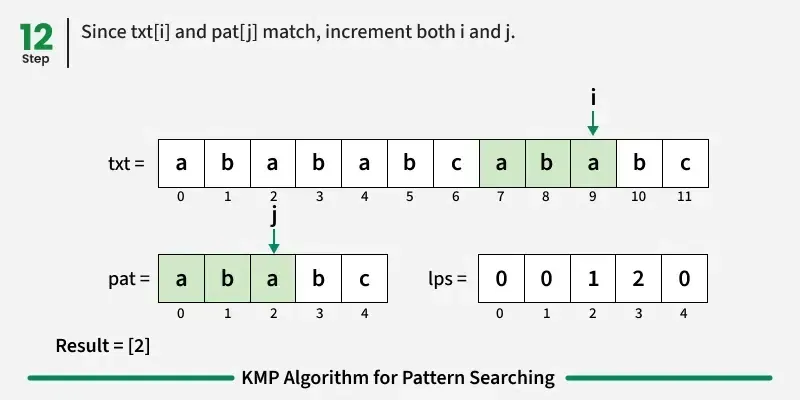
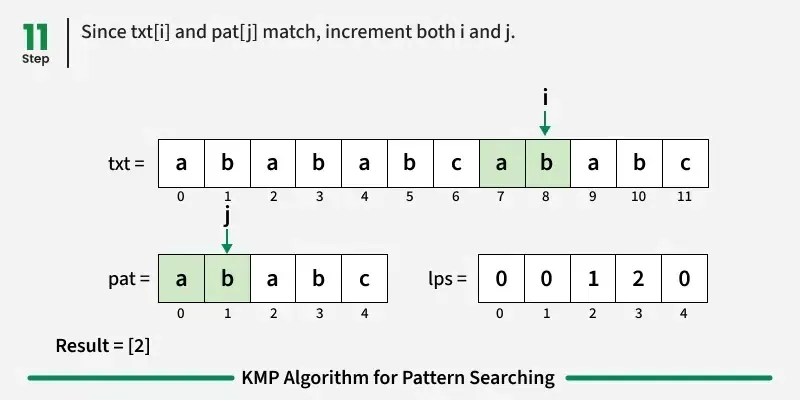
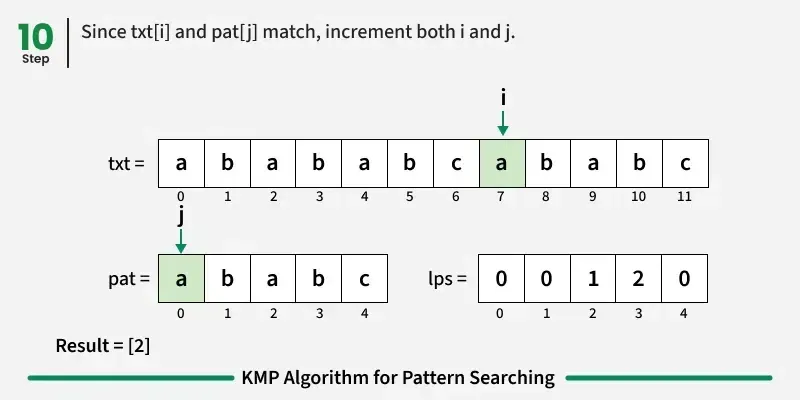
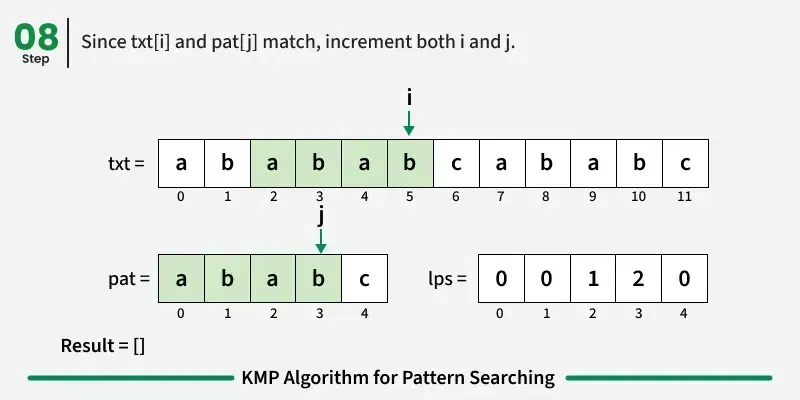
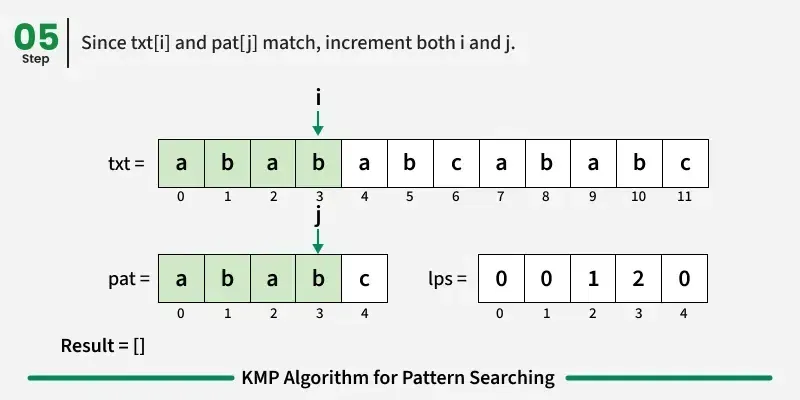
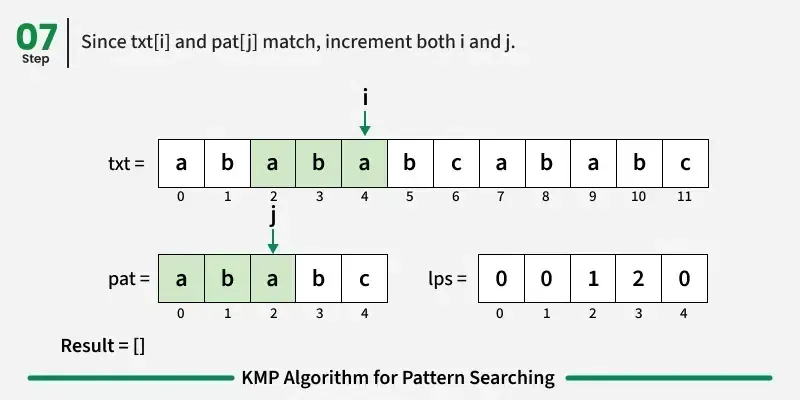
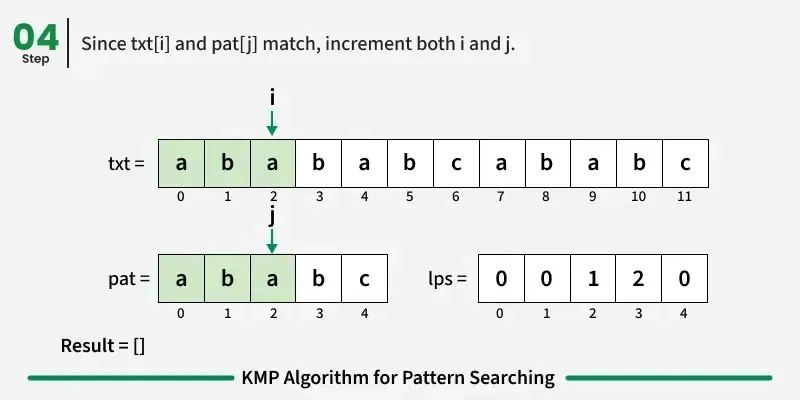
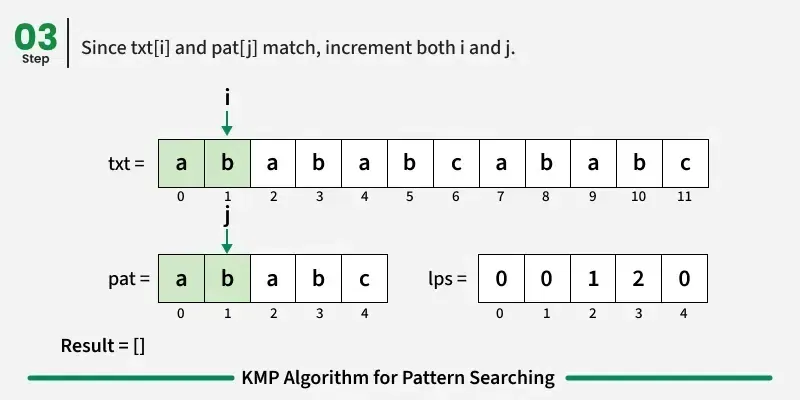
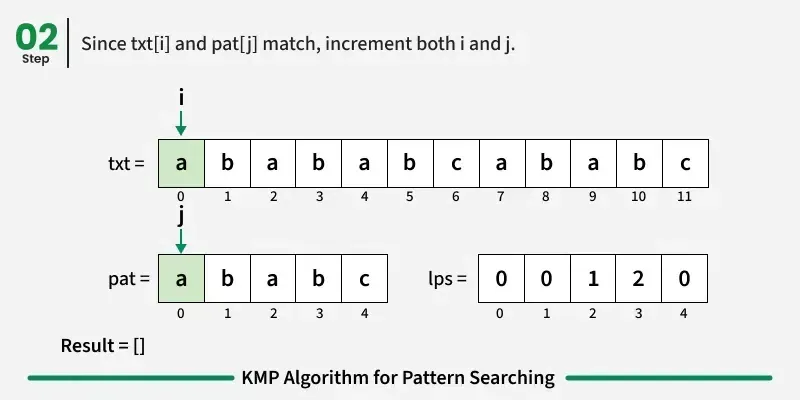
现在，我们开始逐个字符比较图案和文本。

如果字符匹配：在文本和图案中都向前推进。

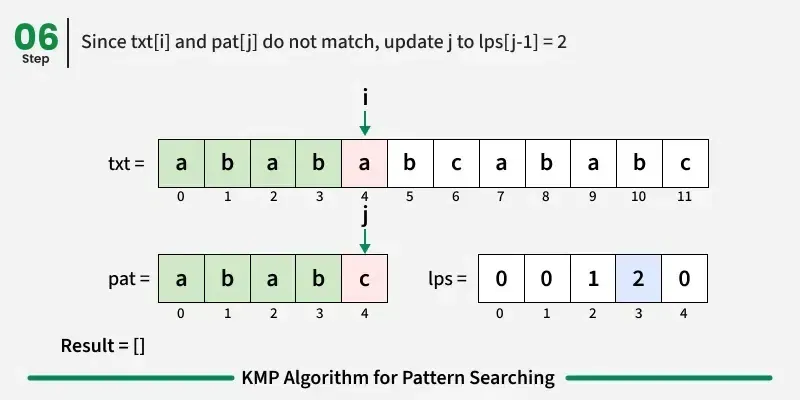
如果字符不匹配：

=> 如果我们不在模式的起点，我们用前一个索引的LPS值（即lps[j - 1]）将图案指针j移回该位置。这意味着：跳到最长且带有后缀的前缀------无需重新检查那些字符。

=> 如果我们处于起点（即 j == 0），只需将文本指针 i 向前移动，尝试下一个字符。

如果我们达到模式的终点（即所有字符都匹配），我们就找到了匹配！记录起始索引并继续搜索。

插图：

import java.util.ArrayList;

class GfG {
    
    static void constructLps(String pat, int[] lps) {
        
        // len stores the length of longest prefix which 
        // is also a suffix for the previous index
        int len = 0;

        // lps[0] is always 0
        lps[0] = 0;

        int i = 1;
        while (i < pat.length()) {
            
            // If characters match, increment the size of lps
            if (pat.charAt(i) == pat.charAt(len)) {
                len++;
                lps[i] = len;
                i++;
            }
            
            // If there is a mismatch
            else {
                if (len != 0) {
                    
                    // Update len to the previous lps value 
                    // to avoid redundant comparisons
                    len = lps[len - 1];
                } 
                else {
                    
                    // If no matching prefix found, set lps[i] to 0
                    lps[i] = 0;
                    i++;
                }
            }
        }
    }

    static ArrayList<Integer> search(String pat, String txt) {
        int n = txt.length();
        int m = pat.length();

        int[] lps = new int[m];
        ArrayList<Integer> res = new ArrayList<>();

        constructLps(pat, lps);

        // Pointers i and j, for traversing 
        // the text and pattern
        int i = 0;
        int j = 0;

        while (i < n) {
            // If characters match, move both pointers forward
            if (txt.charAt(i) == pat.charAt(j)) {
                i++;
                j++;

                // If the entire pattern is matched 
                // store the start index in result
                if (j == m) {
                    res.add(i - j);
                    
                    // Use LPS of previous index to 
                    // skip unnecessary comparisons
                    j = lps[j - 1];
                }
            }
            
            // If there is a mismatch
            else {
                
                // Use lps value of previous index
                // to avoid redundant comparisons
                if (j != 0)
                    j = lps[j - 1];
                else
                    i++;
            }
        }
        return res; 
    }

    public static void main(String[] args) {
        String txt = "aabaacaadaabaaba"; 
        String pat = "aaba"; 

        ArrayList<Integer> res = search(pat, txt);
        for (int i = 0; i < res.size(); i++) 
            System.out.print(res.get(i) + " ");
    }
}

输出

0 9 12

时间复杂度：O（n + m），其中n为文本长度，m为图案长度。这是因为创建LPS（最长前缀后缀）数组需要O（m）时间，而文本搜索则需要O（n）时间。

辅助空间：O（m），因为我们需要存储大小为m的LPS数组。

KMP的优点

线性时间复杂度。

文本中没有任何倒退。

对于大规模文本搜索（如日志分析、DNA测序）非常高效。

现实应用

文本编辑器（查找功能）

抄袭检测

生物信息学（DNA序列匹配）

垃圾邮件检测系统

搜索引擎

编程资源
https://pan.quark.cn/s/7f7c83756948
更多资源
https://pan.quark.cn/s/bda57957c548