MATLAB control system model

开环控制

复制代码

s = tf('s'); 
P_pitch = (1.151*s+0.1774)/(s^3+0.739*s^2+0.921*s);

% Q1-2
t = [0:0.01:10]; 
step(0.2*P_pitch,t); % input delta = 0.2
xlim([0 10]);
ylim([0 0.8]);
ylabel('pitch angle (rad)'); 
title('Open-loop Step Response');

% Q3-4
pole(P_pitch)

闭环控制

复制代码

s = tf('s'); 
P_pitch = (1.151*s+0.1774)/(s^3+0.739*s^2+0.921*s);
C = 1; 
sys_cl = feedback(P_pitch,C)

% Q5-8 close loop

%t = [0:0.01:80]; 
% step(0.2*sys_cl,t); % input delta = 0.2

step(0.2*sys_cl); 
ylabel('pitch angle (rad)'); 
title('Closed-loop Step Response');

% Q9
pole(sys_cl)

结果

复制代码

sys_cl = 
 
 1.151 s + 0.1774 
 ---------------------------------- 
 s^3 + 0.739 s^2 + 2.072 s + 0.1774

时域响应

传递函数sys_cl = Y/R.

已知Y是阶跃函数，求Y的时域响应。
zpk是用来给已知的s域多项式做因式分解（分解出极点和零点）

复制代码

R = 0.2/s; 
Y = zpk(sys_cl*R)

结果：

复制代码

Y =
            0.2302 (s+0.1541)
  -------------------------------------
  s (s+0.08805) (s^2 + 0.6509s + 2.015)
  
  =
    A                  B                          Cs+D
  ----    +      ----------------   +      -----------------
    s              (s+0.08805)           (s^2 + 0.6509s + 2.015)

因式分解用 residue 命令，通过进行部分分式展开来确定常数 A、B、C 和 D ，语法为 [r,p,k] = residue(num,den)，其中 num 和 den 分别是包含待展开的拉普拉斯函数的分子和分母系数的数组。注意，数组可能包含零占位符，因为 Y(s) 的分母中没有常数项。

residue有两种语法：

① 分解形式（Partial Fraction Expansion） $r,p,k$ = residue(num,den)

② 还原形式（Reconstruction) $num,den$ = residue(r,p,k)

复制代码

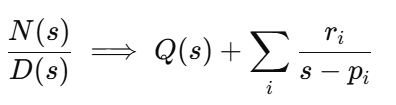
[r,p,k] = residue(0.2*[1.151 0.1774],[1 0.739 2.072 0.1774 0])   %分解形式

结果：

复制代码

r =

  -0.0560 + 0.0160i
  -0.0560 - 0.0160i
  -0.0879 + 0.0000i                 %对应 -0.0881 + 0.0000i
   0.2000 + 0.0000i                 %对应 0.0000 + 0.0000i


p =

  -0.3255 + 1.3816i
  -0.3255 - 1.3816i
  -0.0881 + 0.0000i
   0.0000 + 0.0000i


k =

     []

在上述表达式中，r 是一个数组，包含部分分式展开的留数，即展开式中的分子系数。数组 p 包含系统的极点，其阶数与 r 中留数的阶数相对应。在这种情况下，直接项 k 为空，因为通常情况下，分子多项式的阶数会低于分母多项式的阶数。

r，留数 = 有理函数在某个极点附近的"主导系数"

如果Y(s) = r_i/(s-p_1) + 其他项，那么r_i就是极点p_i的留数。

k，直接项：原有理函数做多项式长除后得到的"商多项式"的系数数组

如果分母次数高于分子，k=\[\]，是空的
r和p对应，排序规则是：

按极点 p 的复数值进行排序。先按实部从大到小 排；若实部相同，再按虚部从大到小排；共轭复数一定成对相邻出现。

基于以上分析，展开式中的系数 A 和 B 分别等于 0.2 和 -0.0879。系数 C 和 D 可以通过将复共轭极点的项合并回一个表达式来确定，如下所示。

复制代码

[num,den] = residue(r(1:2),p(1:2),k);  %还原形式

结果：

复制代码

num =

   -0.1121   -0.0807


den =

    1.0000    0.6509    2.0147

基于以上结果，C = -0.1121，D = -0.08071，我们得到的局部分式展开式可以表示如下。

Tuning

从"调谐方法"下拉菜单中可以选择两个选项："鲁棒响应时间"或"经典设计公式"。

"鲁棒响应时间"算法会自动调整 PID 参数，以平衡响应速度和鲁棒性。它可以调整任何类型 PID 控制器的所有参数，并可用于设计稳定、不稳定或积分型系统。

然而，"经典设计公式"算法要求系统稳定或积分，并且无法调整微分滤波器。如果选择"经典设计公式"算法，则可以在"公式"下拉菜单中看到一系列选项。这些选项包括启发式技术（例如 Ziegler-Nichols 算法）和数值方法，后者会搜索所有可能的控制增益以最小化某些已确定的性能指标。

Root Locus

复制代码

s = tf('s'); 
P_pitch = (1.151*s+0.1774)/(s^3+0.739*s^2+0.921*s);
controlSystemDesigner('rlocus', P_pitch)

controlSystemDesigner导入的是开环传递函数！

直接在designer window里面设置F，C，设定lead还是lag之类的（即确定compensator的零极点）。

Frequency Domain - Bode Diagram

复制代码

s = tf('s'); 
P_pitch = (1.151*s+0.1774)/(s^3+0.739*s^2+0.921*s);

margin(P_pitch), grid

sys_cl = feedback(P_pitch,1); 
step(0.2*sys_cl), grid 
ylabel('pitch angle (rad)'); 
title('Closed-loop Step Response')

margin画的是bode图的magnitude和phase。标注出了幅值裕度和相位裕度。

幅值裕度 (Gain Margin, GM)

定义：在相位达到 -180° 的频率（相位穿越频率）处，系统增益距离 0 dB 还有多少裕量。

相位裕度 (Phase Margin, PM)

定义：在增益达到 0 dB 的频率（增益穿越频率）处，系统相位距离 -180° 还有多少裕量。

直接画Bode图是导入开环传递函数！