19世纪初,当傅里叶在《热的解析理论》中断言"任何周期信号都可表示为正弦级数"时,他或许未曾想到,这一源于热传导研究的数学工具,会成为连接时域与频域的"枢纽"。从泰勒公式的局部幂函数逼进到傅里叶级数的全局谐波分解,从热传导方程的特征解发现到非周期信号的傅里叶变换推广,傅里叶分析的诞生绝非偶然------它是数学上"函数表示法"演进的必然结果,更是物理世界"周期现象描述需求"的直接驱动。
一、数学逻辑:从泰勒公式的"局部精确"到傅里叶级数的"全局分解"
傅里叶级数的诞生,本质是对"函数逼近工具"的一次彻底革新。在它之前,泰勒公式以幂函数( 1 , t , t 2 , ⋯ 1,t,t^2,\cdots 1,t,t2,⋯)为基底,实现了对光滑函数的局部精确描述:对函数 f ( t ) f(t) f(t)在 t 0 t_0 t0处的泰勒展开为:
f ( t ) = ∑ n = 0 ∞ f ( n ) ( t 0 ) n ! ( t − t 0 ) n ( 1 ) f(t) = \sum_{n=0}^{\infty}\frac{f^{(n)}(t_0)}{n!}(t-t_0)^n(1) f(t)=n=0∑∞n!f(n)(t0)(t−t0)n(1) 这种方法对 e t e^t et、 sin t \sin t sint等光滑函数效果显著,但面对物理世界的周期信号(如声波振动、温度波动)时,却暴露出两大致命局限:
其一,光滑性要求与非光滑信号的矛盾。泰勒级数依赖函数的高阶导数,对包含跳变的信号(如矩形脉冲)会因导数不存在而发散。例如,对周期方波 x ( t ) = rect ( t / τ ) x(t)=\text{rect}(t/\tau) x(t)=rect(t/τ),其在跳变点处导数无穷大,泰勒展开无法收敛。
其二,无界基底与周期现象的矛盾。幂函数 t n t^n tn随时间单调增长,而周期现象具有时间重复性。用泰勒级数逼近周期信号,会得到"幅度随时间无限增大"的非物理结果------这本质是基底函数与物理问题的"特性不匹配"。
傅里叶的突破在于选择三角函数/复指数函数作为新基底。以复指数函数 e j ω t = cos ω t + j sin ω t e^{j\omega t} = \cos\omega t + j\sin\omega t ejωt=cosωt+jsinωt为例,其三大数学特性完美解决了泰勒公式的局限:周期性: e j ω ( t + T ) = e j ω t e^{j\omega(t+T)} = e^{j\omega t} ejω(t+T)=ejωt(周期 T = 2 π / ω T=2\pi/\omega T=2π/ω),天然适配振动、波动等周期过程;正交性:不同频率的复指数函数在周期 T T T内满足 ∫ 0 T e j k ω 0 t ( e j m ω 0 t ) ∗ d t = { T , k = m 0 , k ≠ m \int_{0}^{T}e^{jk\omega_0 t}(e^{jm\omega_0 t})^*dt = \begin{cases} T, & k=m \\ 0, & k\neq m \end{cases} ∫0Tejkω0t(ejmω0t)∗dt={T,0,k=mk=m,确保各分量独立可解,如同向量在正交坐标系中的分解;运算封闭性:微分、积分后仍为复指数函数( d d t e j ω t = j ω e j ω t \frac{d}{dt}e^{j\omega t}=j\omega e^{j\omega t} dtdejωt=jωejωt),大幅简化物理方程求解。
由此,傅里叶级数实现了数学上对周期信号 x ~ ( t ) \tilde{x}(t) x~(t)的分解、表达为复指数分量的叠加:
x ~ ( t ) = ∑ k = − ∞ ∞ c k e j k ω 0 t ( ω 0 = 2 π / T )( 2 ) \tilde{x}(t) = \sum_{k=-\infty}^{\infty}c_k e^{jk\omega_0 t}(\omega_0=2\pi/T)(2) x~(t)=k=−∞∑∞ckejkω0t(ω0=2π/T)(2)
其中系数 c k = 1 T ∫ 0 T x ~ ( t ) e − j k ω 0 t d t c_k = \frac{1}{T}\int_{0}^{T}\tilde{x}(t)e^{-jk\omega_0 t}dt ck=T1∫0Tx~(t)e−jkω0tdt。
但是,事实上傅里叶级数并非纯数学推导的产物,而是19世纪初傅里叶研究热传导问题时的"物理发现"。当时他面临的核心问题是:如何描述均匀物体的温度分布?
对长度为 L L L的均匀杆,温度分布 u ( x , t ) u(x,t) u(x,t)满足热扩散方程 ∂ u ∂ t = α ∂ 2 u ∂ x 2 \frac{\partial u}{\partial t} = \alpha \frac{\partial^2 u}{\partial x^2} ∂t∂u=α∂x2∂2u,边界条件为 u ( 0 , t ) = u ( L , t ) = 0 u(0,t)=u(L,t)=0 u(0,t)=u(L,t)=0。傅里叶假设解的形式为 u ( x , t ) = X ( x ) T ( t ) u(x,t)=X(x)T(t) u(x,t)=X(x)T(t),分离变量后得到:时间方程: T ′ ( t ) + α λ T ( t ) = 0 T'(t) + \alpha \lambda T(t) = 0 T′(t)+αλT(t)=0,解为 T ( t ) = e − α λ t T(t)=e^{-\alpha \lambda t} T(t)=e−αλt(随时间指数衰减);空间方程: X ′ ′ ( x ) + λ X ( x ) = 0 X''(x) + \lambda X(x) = 0 X′′(x)+λX(x)=0,需结合边界条件求解。
在此数学模型下,空间方程的通解自然而然的表达为 X ( x ) = A cos ( λ x ) + B sin ( λ x ) X(x)=A\cos(\sqrt{\lambda}x)+B\sin(\sqrt{\lambda}x) X(x)=Acos(λ x)+Bsin(λ x)。代入边界条件 X ( 0 ) = X ( L ) = 0 X(0)=X(L)=0 X(0)=X(L)=0,得到 sin ( λ L ) = 0 \sin(\sqrt{\lambda}L)=0 sin(λ L)=0,故特征值 λ n = ( n π L ) 2 \lambda_n=(\frac{n\pi}{L})^2 λn=(Lnπ)2,特征函数 X n ( x ) = sin ( n π x L ) X_n(x)=\sin(\frac{n\pi x}{L}) Xn(x)=sin(Lnπx)( n = 1 , 2 , ⋯ n=1,2,\cdots n=1,2,⋯)。这些三角函数是周期的、正交的,且其叠加可表示任意初始温度分布:
u ( x , t ) = ∑ n = 1 ∞ C n sin ( n π x L ) e − α ( n π L ) 2 t ( 3 ) u(x,t) = \sum_{n=1}^{\infty}C_n \sin\left(\frac{n\pi x}{L}\right)e^{-\alpha (\frac{n\pi}{L})^2 t}(3) u(x,t)=n=1∑∞Cnsin(Lnπx)e−α(Lnπ)2t(3)
傅里叶由此断言:任何周期信号都可分解为三角函数的叠加。这一结论最初因缺乏严格证明遭拉格朗日反对,直到1829年狄利克雷提出收敛条件(绝对可积、有限极值点、有限间断点),傅里叶级数的数学合法性才得以确立。
然而,傅里叶级数 x ~ ( t ) = ∑ k = − ∞ ∞ c k e j k ω 0 t \tilde{x}(t) = \sum_{k=-\infty}^{\infty}c_k e^{jk\omega_0 t} x~(t)=∑k=−∞∞ckejkω0t仅适用于周期信号,而现实中的物理信号(如雷达单次脉冲、闪电电磁辐射)多为非周期信号。因此,天才的傅里叶并没有止步于傅里叶级数,而是神来之笔:将非周期信号视为"周期 T → ∞ T\to\infty T→∞的周期信号",通过极限过程将级数推广为积分。傅里叶变换应运而生。
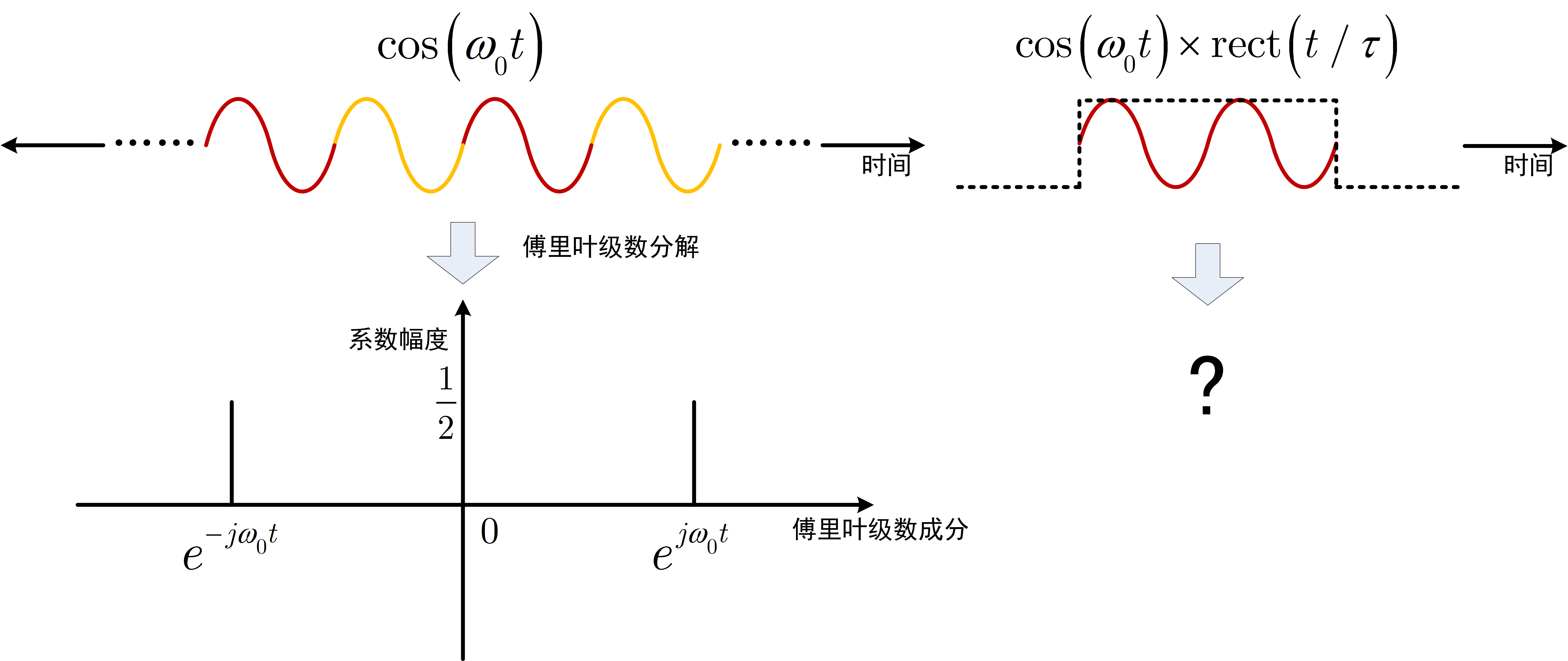
对周期信号,频谱是离散的:频率间隔 Δ ω = ω 0 = 2 π / T \Delta\omega=\omega_0=2\pi/T Δω=ω0=2π/T,系数 c k c_k ck表示各离散频率分量的幅度,因此按照傅里叶的极限思路,当 T → ∞ T\to\infty T→∞: Δ ω → d ω \Delta\omega\to d\omega Δω→dω(频率间隔无穷小),离散频率 k ω 0 k\omega_0 kω0演变为连续频率 ω \omega ω; c k = 1 T X ( j k ω 0 ) → 0 c_k = \frac{1}{T}X(jk\omega_0)\to0 ck=T1X(jkω0)→0,但 T c k T c_k Tck(单位频率内的幅度,即"频谱密度")保持有限,定义为 X ( j ω ) = lim T → ∞ T c k X(j\omega)=\lim_{T\to\infty}T c_k X(jω)=limT→∞Tck 。
将 c k c_k ck的表达式代入 X ( j ω ) X(j\omega) X(jω),即可得到傅里叶正变换:
X ( j ω ) = ∫ − ∞ ∞ x ( t ) e − j ω t d t ( 4 ) X(j\omega) = \int_{-\infty}^{\infty}x(t)e^{-j\omega t}dt(4) X(jω)=∫−∞∞x(t)e−jωtdt(4)
反过来根据数学上的对称关系,有:
{ X ( j ω ) = ∫ − ∞ ∞ x ( t ) e − j ω t d t ⇒ X ( j ω ) ⋅ e j ω τ = ∫ − ∞ ∞ x ( t ) e − j ω t d t ⋅ e j ω τ ⇒ ∫ − ∞ ∞ X ( j ω ) ⋅ e j ω τ d ω = ∫ − ∞ ∞ ∫ − ∞ ∞ x ( t ) e − j ω t d t ⋅ e j ω τ d ω = ∫ − ∞ ∞ ∫ − ∞ ∞ x ( t ) e − j ω ( τ − t ) d t ⋅ d ω = ∫ − ∞ ∞ ∫ − ∞ ∞ x ( t ) e − j ω ( τ − t ) d ω ⋅ d t = ∫ − ∞ ∞ x ( t ) 2 π δ ( τ − t ) d t = 2 π x ( t ) ( 5 ) \begin{cases} & X(j\omega )=\int_{-\infty }^{\infty }{x(t){{e}^{-j\omega t}}}dt\Rightarrow \\ & X(j\omega )\cdot {{e}^{j\omega \tau }}=\int_{-\infty }^{\infty }{x(t){{e}^{-j\omega t}}}dt\cdot {{e}^{j\omega \tau }}\Rightarrow \\ & \int_{-\infty }^{\infty }{X(j\omega )\cdot {{e}^{j\omega \tau }}}d\omega \\ & =\int_{-\infty }^{\infty }{\int_{-\infty }^{\infty }{x(t){{e}^{-j\omega t}}}dt\cdot {{e}^{j\omega \tau }}}d\omega \\ & =\int_{-\infty }^{\infty }{\int_{-\infty }^{\infty }{x(t){{e}^{-j\omega \left( \tau -t \right)}}dt}}\cdot d\omega \\ & =\int_{-\infty }^{\infty }{\int_{-\infty }^{\infty }{x(t){{e}^{-j\omega \left( \tau -t \right)}}d\omega \cdot }}dt \\ & =\int_{-\infty }^{\infty }{x(t)2\pi \delta \left( \tau -t \right)dt} \\ & =2\pi x(t) \\ \end{cases}(5) ⎩ ⎨ ⎧X(jω)=∫−∞∞x(t)e−jωtdt⇒X(jω)⋅ejωτ=∫−∞∞x(t)e−jωtdt⋅ejωτ⇒∫−∞∞X(jω)⋅ejωτdω=∫−∞∞∫−∞∞x(t)e−jωtdt⋅ejωτdω=∫−∞∞∫−∞∞x(t)e−jω(τ−t)dt⋅dω=∫−∞∞∫−∞∞x(t)e−jω(τ−t)dω⋅dt=∫−∞∞x(t)2πδ(τ−t)dt=2πx(t)(5)
即得到傅里叶逆变换通过积分重构信号:
x ( t ) = 1 2 π ∫ − ∞ ∞ X ( j ω ) e j ω t d ω ( 6 ) x(t) = \frac{1}{2\pi}\int_{-\infty}^{\infty}X(j\omega)e^{j\omega t}d\omega(6) x(t)=2π1∫−∞∞X(jω)ejωtdω(6)
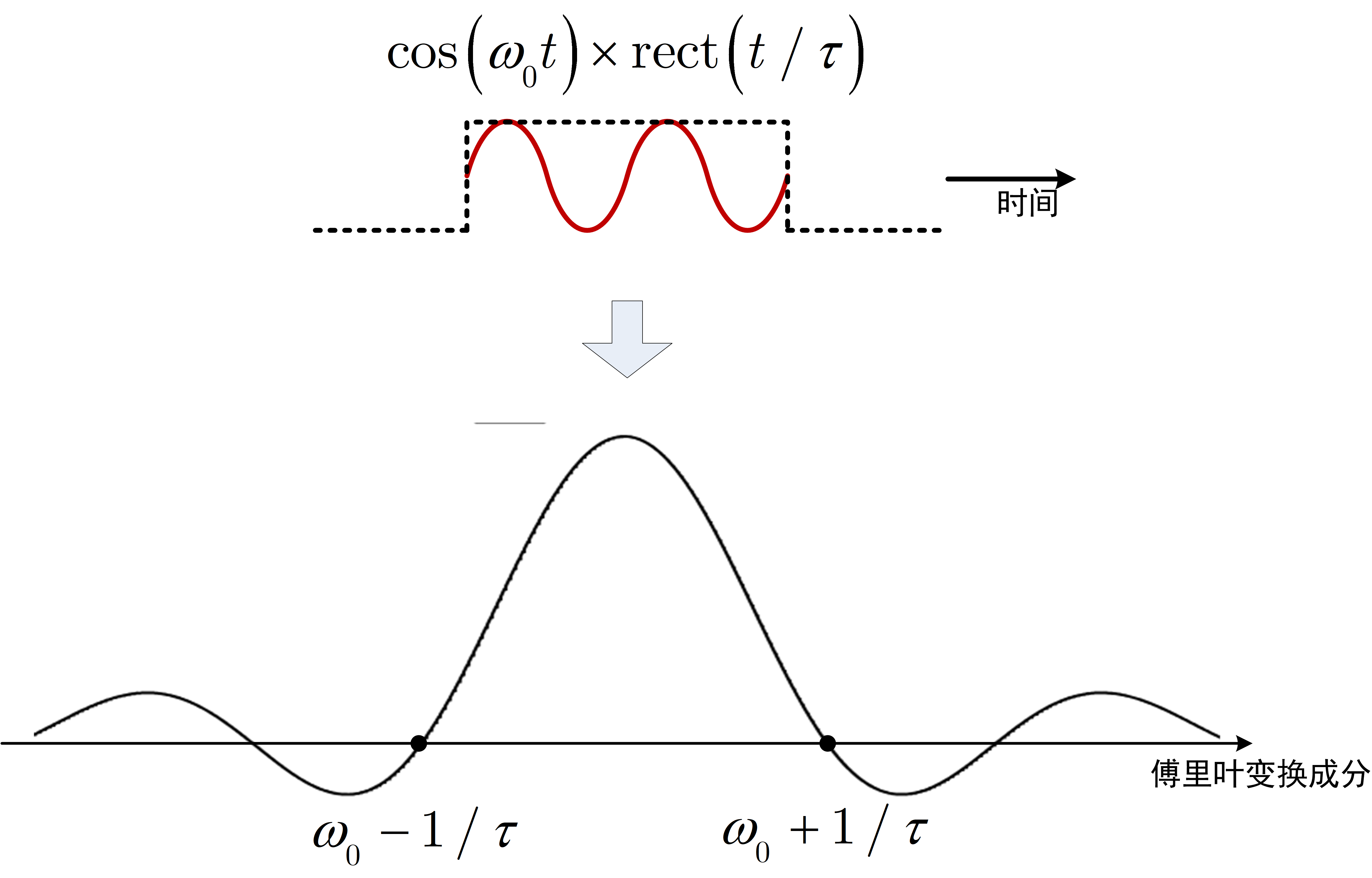
这意味着:非周期信号是连续频率复指数信号的积分叠加, ∣ X ( j ω ) ∣ |X(j\omega)| ∣X(jω)∣为"频谱密度",描述单位频率内的能量分布。例如,矩形脉冲的傅里叶变换为 X ( j ω ) = τ sinc ( ω τ / 2 ) X(j\omega)=\tau\text{sinc}(\omega\tau/2) X(jω)=τsinc(ωτ/2),其频域主瓣宽度与脉宽 τ \tau τ成反比,直观展示了"时域越窄,频域越宽"的物理规律。
傅里叶变换的诞生,是数学逻辑与物理需求的完美融合:泰勒公式的局限催生了基底革命,热传导方程的求解推动了级数理论,非周期信号的描述需求最终完成了从级数到变换的推广。如今,从雷达信号处理到图像处理,从量子力学到深度学习,傅里叶分析已成为科学研究的"通用语言"------它不仅是一种数学工具,更是一种"透过时域表象洞察频域本质"的思维范式,持续影响着人类对自然规律的认知。