在《跟踪导论(七)》中阐述了卡尔曼滤波各参数的联动方式,即:
x˙[n]=Fx^[n−1](1){\bf{\dot x}}\left[ n \right] = {\bf{F\hat x}}\left[ {n - 1} \right](1)x˙[n]=Fx^[n−1](1)
M˙[n]=F⋅M^[n−1]⋅FT+g⋅q⋅gT(2){\bf{\dot M}}\left[ n \right] = {\bf{F}} \cdot {\bf{\hat M}}\left[ {n - 1} \right] \cdot {{\bf{F}}^T} + {\bf{g}} \cdot {\bf{q}} \cdot {{\bf{g}}^T}(2)M˙[n]=F⋅M^[n−1]⋅FT+g⋅q⋅gT(2)
k[n]=M˙[n]σw[n]2+M˙[n](σ~2=σw[n]2)(3){\bf{k}}\left[ n \right] = {{{\bf{\dot M}}\left[ n \right]} \over {\sigma _{{\bf{w}}\left[ n \right]}^2 + {\bf{\dot M}}\left[ n \right]}}\left( {{{\tilde \sigma }^2} = \sigma _{{\bf{w}}\left[ n \right]}^2} \right)(3)k[n]=σw[n]2+M˙[n]M˙[n](σ~2=σw[n]2)(3)
M^[n]=(I−k[n])M˙[n](4){\bf{\hat M}}\left[ n \right] = \left( {{\bf{I}} - {\bf{k}}\left[ n \right]} \right){\bf{\dot M}}\left[ n \right](4)M^[n]=(I−k[n])M˙[n](4)
x^[n]=x˙[n]+k[n](hT[n]x~[n]−hT[n]x˙[n])(5){\bf{\hat x}}\left[ n \right] = {\bf{\dot x}}\left[ n \right] + {\bf{k}}\left[ n \right]\left( {{{\bf{h}}^{\bf{T}}}\left[ n \right]{\bf{\tilde x}}\left[ n \right] - {{\bf{h}}^{\bf{T}}}\left[ n \right]{\bf{\dot x}}\left[ n \right]} \right)(5)x^[n]=x˙[n]+k[n](hT[n]x~[n]−hT[n]x˙[n])(5)
其中k{\bf{k}}k为卡尔曼增益、M{\bf{M}}M为预测均方误差(M˙{\bf{\dot M}}M˙为预测的预测均方误差、M^{\bf{\hat M}}M^为修正后的预测均方误差)、F{\bf{F}}F为状态转移矩阵、q{\bf{q}}q为目标运动过程噪声、σw[n]2\sigma _{{\bf{w}}\left[ n \right]}^2σw[n]2为观测噪声、x˙{\bf{\dot x}}x˙为根据上一时刻目标运动状态对当下时刻目标运动状态的估计值、x~[n]{\bf{\tilde x}}\left[ n \right]x~[n]为对当下时刻目标状态的观测值、x^[n]{\bf{\hat x}}\left[ n \right]x^[n]为对当下时刻目标状态的卡尔曼滤波算法估计值、h{\bf{h}}h常为[1,0]T{[1,0]^{\rm{T}}}[1,0]T(考虑目标仅在雷达径向上一维运动)、σ~2{\tilde \sigma ^2}σ~2为观测预测误差σ~2=(hT[n]x~[n]−hT[n]x˙[n])2{\tilde \sigma ^2} = {\left( {{{\bf{h}}^{\bf{T}}}\left[ n \right]{\bf{\tilde x}}\left[ n \right] - {{\bf{h}}^{\bf{T}}}\left[ n \right]{\bf{\dot x}}\left[ n \right]} \right)^2}σ~2=(hT[n]x~[n]−hT[n]x˙[n])2。那么我们在实际的卡尔曼滤波工程实践中,这种联动是怎么启动的呢?也就是说这些参数的初始参数是如何进行合理设置的?
一、目标初始状态信息的获取
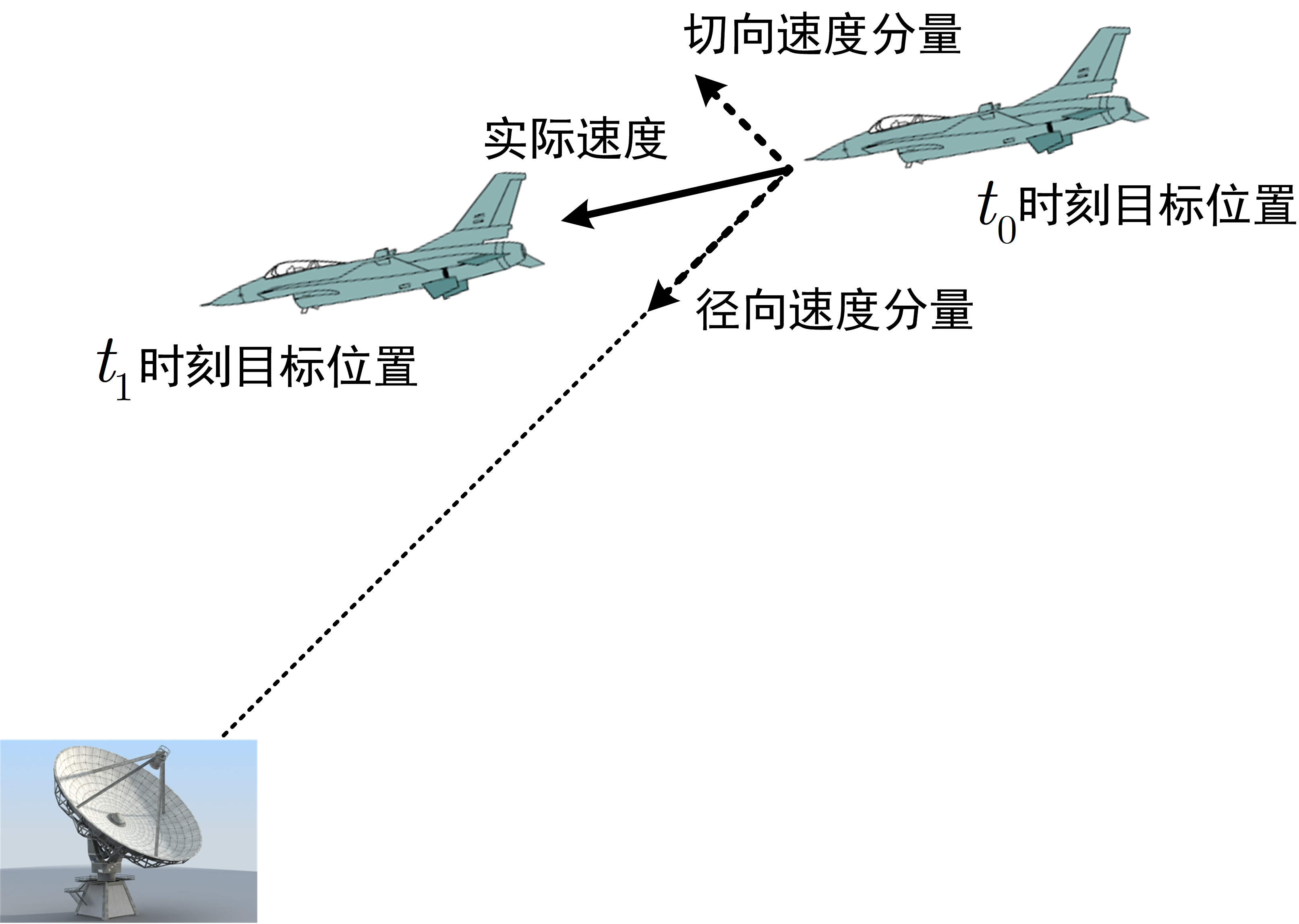
事实上,我们在雷达探测中都是采用先发现后跟踪的方式,雷达首先通过在一定方位内进行扫描获得目标的初始位置信息即在t0{t_0}t0时刻有x~[0]=[z~[0],0]T{\bf{\tilde x}}\left[ 0 \right] = {\left[ {\tilde z\left[ 0 \right],0} \right]^{\rm{T}}}x~[0]=[z~[0],0]T,此时雷达仅为了发现目标进行预警,因此通常采用大重复周期进行探测、不进行多普勒测速。同时,此时雷达的观测数据没有任何的历史信息可以进行修正,因此,雷达认为当下初始时刻的观测数据就是估计数据即x^[0]=x~[0]{\bf{\hat x}}\left[ 0 \right] = {\bf{\tilde x}}\left[ 0 \right]x^[0]=x~[0]。在t1{t_1}t1时刻,雷达通常有两种方式获取目标运动状态信息:一种是由于目标距离通常较远,雷达仅采用大重复周期波形进行探测,那就依然仅能获取目标的位置信息z~[1]\tilde z\left[ 1 \right]z~[1],但目标的速度信息可通过两次观测位置差间接得到,即假设雷达观测的时间间隔为TTT,则目标的速度信息为v~[1]=(z~[1]−z~[0])/T\tilde v\left[ 1 \right] = \left( {\tilde z\left[ 1 \right] - \tilde z\left[ 0 \right]} \right)/Tv~[1]=(z~[1]−z~[0])/T,此时可获得目标的运动状态信息x^[1]=x~[1]=(z~[1],v~[1]){\bf{\hat x}}\left[ 1 \right] = {\bf{\tilde x}}\left[ 1 \right] = \left( {\tilde z\left[ 1 \right],\tilde v\left[ 1 \right]} \right)x^[1]=x~[1]=(z~[1],v~[1]);另一种方式是雷达在当下时刻采用大重复周期和和短重复周期波形接续进行测距z~[1]\tilde z\left[ 1 \right]z~[1]和测速v~[1]\tilde v\left[ 1 \right]v~[1],那么此时也可获得目标的运动状态信息。通常情况下,雷达会采用第一种方式获得目标运动状态信息,这是因为目标通常是在三维空间中运动的,也就是说目标相对于雷达的运动通常是由径向的运动和非径向的运动构成,而雷达多普勒测速仅能实现径向测速,第一种方式雷达通过两次测量的位置差获取目标的速度即可同时获得目标在径向和非径向上的运动速度,如图1所示。观察公式(1)和(2)可知,确定目标初始状态信息后,下一步即是状态转移矩阵F{\bf{F}}F和目标运动过程噪声q{\bf{q}}q的设定。
二、目标状态转移矩阵F{\bf{F}}F和运动过程噪声q{\bf{q}}q的设定
目标状态转移矩阵F{\bf{F}}F和运动过程噪声q{\bf{q}}q的设定是雷达依靠主观上对目标客观运动状态的猜测而设定。首先看过程噪声q=(σqx2ρσqxσqyρσqxσqyσqy2)\mathbf{q} = \begin{pmatrix} \sigma_{qx}^2 & \rho_{\sigma_{qx}\sigma_{qy}} \\ \rho_{\sigma_{qx}\sigma_{qy}} & \sigma_{qy}^2 \end{pmatrix}q=(σqx2ρσqxσqyρσqxσqyσqy2)
(若考虑目标只在一维上运动则q=σq2{\bf{q}} = \sigma _q^2q=σq2),雷达设定的过程噪声通常是根据一般运动目标的一般运动特性来设定,一般雷达将过程噪声表征在加速度上,即目标加速度的扰动功率,该数值越大,则表示目标在一步采样内位置或速度可能发生的随机跳动越剧烈;调大其功率σq2\sigma q^2σq2等价于更"相信"目标会突然加减速,从而增益变大、响应变快但平滑性下降,通常雷达根据经验公式σq2=(amax/3)2\sigma q^2 = {\left( {{a{\max }}/3} \right)^2}σq2=(amax/3)2进行设置,amax{a{\max }}amax是目标最大加速度。
而对于目标状态转移矩阵F{\bf{F}}F,由于雷达的观测间隔通常很短,因此对于宏观运动目标,雷达常采用匀速、匀加速、匀转弯三种模型即:
匀速:F=(1T01)(6)\mathbf{F} = \begin{pmatrix} 1 & T \\ 0 & 1 \end{pmatrix}(6)F=(10T1)(6)
匀加速:F=(1T1/2T201T001)(7)\mathbf{F} = \begin{pmatrix} 1 & T & 1/2T^2\\ 0 & 1 & T\\ 0 & 0 & 1 \end{pmatrix}(7)F= 100T101/2T2T1 (7)
匀转弯:F=(10T0010T001−ωT00ωT1)(8)\mathbf{F} = \begin{pmatrix} 1 & 0 & T & 0 \\ 0 & 1 & 0 & T \\ 0 & 0 & 1 & { - \omega T} \\ 0 & 0 & {\omega T} & 1 \end{pmatrix}(8)F= 10000100T01ωT0T−ωT1 (8)
三、预测均方矩阵M{\bf{M}}M的初始值设定
首先,我们先来确定预测均方矩阵M{\bf{M}}M中每个元素的含义,设F=(M11M12M21M22)\mathbf{F} = \begin{pmatrix} {{M_{11}}} & {{M_{12}}} \\ {{M_{21}}} & {{M_{22}}} \end{pmatrix}F=(M11M21M12M22)(以状态矩阵仅有位置和速度为例),则其中M11{M_{11}}M11表征的是雷达通过历史信息推断的目标位置与真实目标位置的误差即M11=E{(z˙−z)2}{M_{11}} = E\left\{ {{{\left( {\dot z - z} \right)}^2}} \right\}M11=E{(z˙−z)2},M22{M_{22}}M22表征的是雷达通过历史信息推断的目标速度与真实目标速度的误差即M22=E{(v˙−v)2}{M_{22}} = E\left\{ {{{\left( {\dot v - v} \right)}^2}} \right\}M22=E{(v˙−v)2},M12{M_{12}}M12、M21{M_{21}}M21表征的是雷达通过历史信息的推断目标位置与真实目标位置的误差和推断目标速度与真实目标速度误差的协方差即M12=M21=E{(z˙−z)(v˙−v)}{M_{12}} = {M_{21}} = E\left\{ {\left( {\dot z - z} \right)\left( {\dot v - v} \right)} \right\}M12=M21=E{(z˙−z)(v˙−v)}。若假设目标为匀速直线运动、速度为vvv,则在t0{t_0}t0时刻和t1{t_1}t1时刻目标位置的观测值z~[0]\tilde z\left[ 0 \right]z~[0]、z~[1]\tilde z\left[ 1 \right]z~[1]可表示为:
z~[0]=z[0]+w[0](9)\tilde z\left[ 0 \right] = z\left[ 0 \right] + w\left[ 0 \right](9)z~[0]=z[0]+w[0](9)
z~[1]=z[1]+w[1]=z[0]+vT+w[1](10)\tilde z\left[ 1 \right] = z\left[ 1 \right] + w\left[ 1 \right] = z\left[ 0 \right] + vT + w\left[ 1 \right](10)z~[1]=z[1]+w[1]=z[0]+vT+w[1](10)
其中w[0]w\left[ 0 \right]w[0]和w[1]w\left[ 1 \right]w[1]分别t0{t_0}t0时刻的观测噪声和t1{t_1}t1时刻的观测噪声。那么M11[0]{M_{11}}\left[ 0 \right]M11[0]、M22[0]{M_{22}}\left[ 0 \right]M22[0]、M12[0]{M_{12}}\left[ 0 \right]M12[0]、M21[0]{M_{21}}\left[ 0 \right]M21[0]可分别表示为:
M11[0]=E{(z˙[0]−z[0])2}==E{(w[0])2}(11){M_{11}}\left[ 0 \right] = E\left\{ {{{\left( {\dot z\left[ 0 \right] - z\left[ 0 \right]} \right)}^2}} \right\} = = E\left\{ {{{\left( {w\left[ 0 \right]} \right)}^2}} \right\}(11)M11[0]=E{(z˙[0]−z[0])2}==E{(w[0])2}(11)
M22[0]=E{(v˙−v)2}=E{((z~[1]−z~[0])/T−v)2}=E{(v+w[1]−w[0]T−v)2}=E{(w[1]−w[0]T)2}(12){M_{22}}\left[ 0 \right] = E\left\{ {{{\left( {\dot v - v} \right)}^2}} \right\} = E\left\{ {{{\left( {\left( {\tilde z\left[ 1 \right] - \tilde z\left[ 0 \right]} \right)/T - v} \right)}^2}} \right\} = E\left\{ {{{\left( {v + {{w\left[ 1 \right] - w\left[ 0 \right]} \over T} - v} \right)}^2}} \right\} = E\left\{ {{{\left( {{{w\left[ 1 \right] - w\left[ 0 \right]} \over T}} \right)}^2}} \right\}(12)M22[0]=E{(v˙−v)2}=E{((z~[1]−z~[0])/T−v)2}=E{(v+Tw[1]−w[0]−v)2}=E{(Tw[1]−w[0])2}(12)
M22[0]=E{(v˙−v)2}=E{((z~[1]−z~[0])/T−v)2}=E{(v+w[1]−w[0]T−v)2}=E{(w[1]−w[0]T)2}(13){M_{22}}\left[ 0 \right] = E\left\{ {{{\left( {\dot v - v} \right)}^2}} \right\} = E\left\{ {{{\left( {\left( {\tilde z\left[ 1 \right] - \tilde z\left[ 0 \right]} \right)/T - v} \right)}^2}} \right\} = E\left\{ {{{\left( {v + {{w\left[ 1 \right] - w\left[ 0 \right]} \over T} - v} \right)}^2}} \right\} = E\left\{ {{{\left( {{{w\left[ 1 \right] - w\left[ 0 \right]} \over T}} \right)}^2}} \right\}(13)M22[0]=E{(v˙−v)2}=E{((z~[1]−z~[0])/T−v)2}=E{(v+Tw[1]−w[0]−v)2}=E{(Tw[1]−w[0])2}(13)
M12[0]=M21[0]=E{(z˙[0]−z[0])(v˙−v)}=E{w[0]⋅w[1]−w[0]T}(14){M_{12}}\left[ 0 \right] = {M_{21}}\left[ 0 \right] = E\left\{ {\left( {\dot z\left[ 0 \right] - z\left[ 0 \right]} \right)\left( {\dot v - v} \right)} \right\} = E\left\{ {w\left[ 0 \right] \cdot {{w\left[ 1 \right] - w\left[ 0 \right]} \over T}} \right\}(14)M12[0]=M21[0]=E{(z˙[0]−z[0])(v˙−v)}=E{w[0]⋅Tw[1]−w[0]}(14)
通常情况下假设雷达是在白噪声环境下观测目标,则w[0]w\left[ 0 \right]w[0]和w[1]w\left[ 1 \right]w[1]不相关,且均值为0,则,由此得到:M12[0]=M21[0]=−E{(w[0])2}/T=−σw2/T{M_{12}}\left[ 0 \right] = {M_{21}}\left[ 0 \right] = - E\left\{ {{{\left( {w\left[ 0 \right]} \right)}^2}} \right\}/T = - \sigma w^2/TM12[0]=M21[0]=−E{(w[0])2}/T=−σw2/T、小于0,而M11[0]=σw2{M{11}}\left[ 0 \right] = \sigma w^2M11[0]=σw2、M22[0]=E{(w[1]−w[0])2}/T=2σw2/T{M{22}}\left[ 0 \right] = E\left\{ {{{\left( {w\left[ 1 \right] - w\left[ 0 \right]} \right)}^2}} \right\}/T = 2\sigma _w^2/TM22[0]=E{(w[1]−w[0])2}/T=2σw2/T、大于0,即:
M[0]=(σw2−σw2/T−σw2/T2σw2/T)(15)M[0] = \begin{pmatrix} \sigma_w^2 & -\sigma_w^2/T \\ -\sigma_w^2/T& 2\sigma_w^2/T \end{pmatrix}(15)M[0]=(σw2−σw2/T−σw2/T2σw2/T)(15)