基于MATLAB的麦克风音频效果测试

本设计报告是福州大学数字信号处理课程的课外作业之麦克风性能测试（快速傅里叶变换的验证、频谱分析），本次课程设计报告获得A+，供各位学弟学妹参考。这个课程设计主要是加强对FFT，傅里叶变换的理解，通过对MATLAB的程序编写，对关键参数的修改，既加深了对MATLAB代码的理解，又能切身感受到FFT的关键参数，如采样频率、采样点数等对频谱分析结果的影响；进一步对结果进行归一化处理、去噪声门槛设置等，更考验了我们的工程能力；对于谐波分量的观察，可以加深我们对理论的理解（傅里叶级数展开），通过实际工程验证理论，正所谓教学与实践合一。

摘要

本测试旨在利用 MATLAB 软件平台，通过编写脚本对麦克风进行音频数据采集与FFT快速傅里叶变换处理分析。通过代码修改，解决了录音设备启动时的硬件延迟（Cold Start Latency）问题，通过数据截取算法保证了分析数据的有效性；通过对频谱幅度的归一化以及对频率索引的换算，得出归一化频率谱。测试核心内容包括：(1) 输入标准方波信号，分析麦克风对基波及奇次谐波（3次、5次、7次）的响应比例，以验证其线性度与失真情况；(2) 分析频谱图高频衰减特性，确定麦克风的最高有效响应频率。实验结果以时域波形图和带有自动峰值标注的频域图呈现。测试结果表明，该麦克风在指定频率范围内表现出良好的频响特性，谐波衰减基本符合理论预期。

关键词：麦克风；matlab；快速傅里叶变换；频谱分析

Abstract

This test utilized MATLAB for microphone audio acquisition and FFT analysis. Code modifications resolved hardware startup delay via data truncation, ensuring valid data. Spectral normalization yielded normalized frequency spectra. Core analyses included:

(1) Applying a square wave to measure response to the fundamental and odd harmonics (3rd, 5th, 7th), assessing linearity and distortion; (2) Determining the highest effective response frequency from high-frequency roll-off in the spectrum. Results are shown as time-domain waveforms and automatically annotated frequency-domain plots.

Keywords: microphone; MATLAB; Fast Fourier Transform; spectral analysis

一、引言

1.1 研究背景与意义

麦克风作为声电转换的关键器件，在音频采集设备的质量评估中，频率响应特性是衡量麦克风性能的关键指标之一。理想的麦克风应当具备平坦的频响曲线，但在实际应用中，受限于换能器物理特性、电路设计等因素，不同频率成分的增益会有所差异。方波信号因包含丰富的奇次谐波成分，是评估麦克频率响应特性的有效激励信号。在数字化测试中，常见的挑战包括系统启动延迟导致的无效数据段，以及如何精确量化谐波分量。

1.2 测试目的

通过采集标准方波信号，分析麦克风对各次谐波的响应情况。
验证方波基波、三次波、五次波、七次波的幅度衰减规律。
测定麦克风在特定条件下的最高响应频率。
建立基于Matlab的自动化麦克风测试流程。

二、测试系统与方案

2.1 硬件配置

信号源：网页/音频信号发生器（产生标准方波信号）

https://www.onlinemictest.com/zh/tone-generator/

待测设备：待测麦克风

产品参数

单体电容式

指向性：单指向

频率响应：70Hz-15kHz

灵敏度：-47dB±3dB(OdB=1V/Pa at 1kHz)

输出阻抗：680Ω±30%(at 1kHz)

工作电压：1.5-0V

声学环境：正常宿舍环境
采集系统：计算机声卡接口

2.2 软件配置

Matlab 复制代码

开发环境：Matlab R2023b

核心采样参数：

fs = 48000;          % 采样频率

T  = 1/fs ;         % 采样间隔

N  = 48000;         % 采样点数

record_time = N*T;  % 记录时间

bits = 16;          % 采样位数

channel = 1;        % 采样通道

2.3测试策略

本测试方案采用 audiorecorder 对象进行数据流采集，并实施了以下改进策略：

（1）延迟补偿：在代码层面设定 17000 个采样点（约 0.7秒）的缓冲截取区，剔除硬件初始化时的不稳定数据。

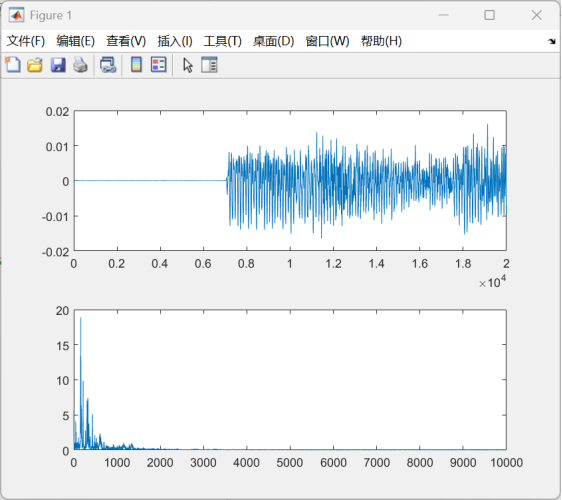
如图所示，在第一幅图中的7000点以前的时域波形为空，根据多次实验判断为是程序调动录音设备启动时的硬件延迟（Cold Start Latency）问题。为解决该问题，我采用截取有效数据段的方式，采取更多的点，截取有效部分。

对于recordblocking延长了采样时间为17000/fs 秒，即多采集17000个点的数据。而在对数据截取17000点之后的数据，避免取空。同时对时域幅值进行归一化，以便于观察幅值之比，对处理过后的数据点再进行FFT变换，代码如下:

Matlab 复制代码

recordblocking(lineinput, record_time+17000/fs);

raw_data = getaudiodata(lineinput);

data = raw_data(17000+1:end);

% 幅值归一化

data = data / max(abs(data)); % 时域归一化到[-1, 1]

% 计算FFT

mag_frequence = abs(fft(data));

（2）自动峰值检测：利用 findpeaks 函数自动定位频谱中的关键频率点，便于直接读取谐波幅值。

Matlab 复制代码

% 峰值检测参数

min_peak_height = 0.1;  % 归一化后阈值设为0.1

min_peak_distance = 10;  % 最小频率间隔

% 自动识别频谱峰值

[peak_values, peak_indices] = findpeaks(mag_frequence,

 'MinPeakHeight', min_peak_height, ...

'MinPeakProminence', min_peak_height/2, ...

'MinPeakDistance', min_peak_distance);

（3）归一化处理：对时域和频域数据进行幅值归一化，消除录音增益差异，便于横向对比标准理论值。

Matlab 复制代码

% 峰值检测参数

min_peak_height = 0.1;  % 归一化后阈值设为0.1

min_peak_distance = 10;  % 最小频率间隔

% 自动识别频谱峰值

[peak_values, peak_indices] = findpeaks(mag_frequence,

 'MinPeakHeight', min_peak_height, ...

'MinPeakProminence', min_peak_height/2, ...

'MinPeakDistance', min_peak_distance);

2.4测试原理

根据数字信号处理理论，一个理想的方波是由基波和无穷多个奇次谐波组成的。其傅里叶级数展开式为：

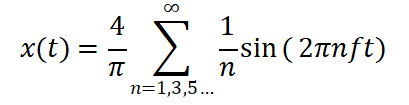
这意味着，在理想无失真的情况下，各次谐波的幅度比例应严格遵循：

测试判定标准：观察 MATLAB 生成的频谱图峰值，若各次谐波幅值比例接近 1 : 0.33 : 0.2 : 0.14，则说明麦克风在中低频段具有良好的平坦度和瞬态响应能力。

三、测试数据与结果

3.1 方波测试结果分析

运行代码并播放 1000Hz 标准方波，观察频谱结果。

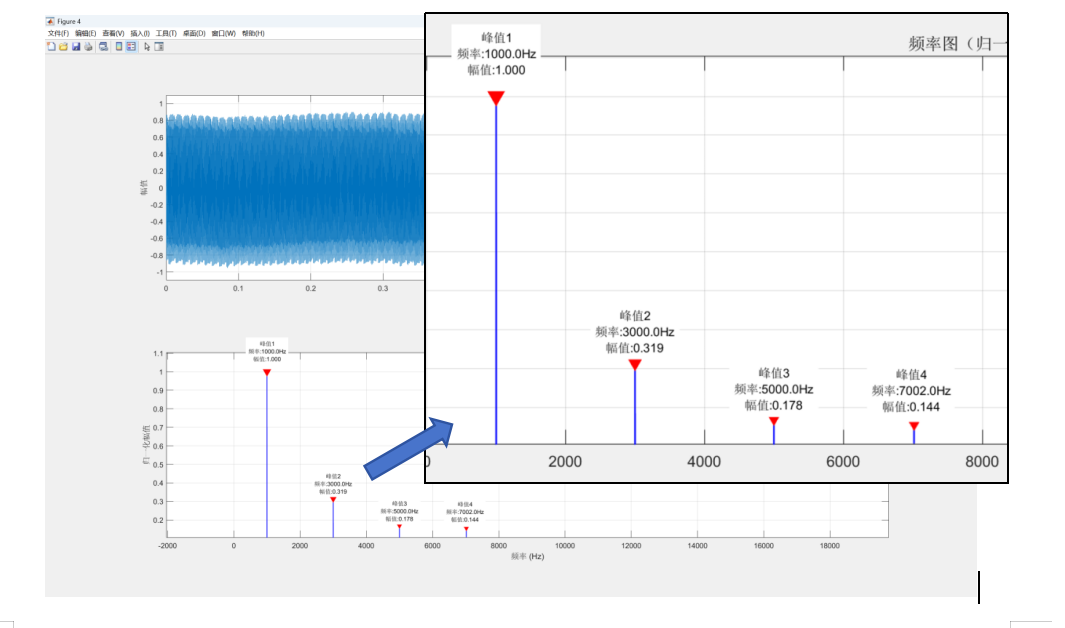
3 .2 实测频谱数据

从频率图中检测到的主要谐波成分如下：

|----------|----------|-----------|-----------|----------|-----------|----------|
| 谐波次数 | 理论频率 | 实测频率 | 理论幅值比 | 实测幅值 | 实测/理论 | 相对误差 |
| 基波 (1次) | 1000 Hz | 1000.0 Hz | 1.0 | 1.0 | 1.0 | 0.0% |
| 3次谐波 | 3000 Hz | 3000.0 Hz | 0.333 | 0.319 | 0.958 | 4.2% |
| 5次谐波 | 5000 Hz | 5000.0 Hz | 0.200 | 0.178 | 0.890 | 11.0% |
| 7次谐波 | 7000 Hz | 7000.0 Hz | 0.143 | 0.144 | 1.007 | 0.7% |

3 .3 谐波衰减规律分析

理论衰减序列：1 : 1/3 : 1/5 : 1/7 ≈ 1 : 0.333 : 0.200 : 0.143

实测衰减序列：1 : 0.319 : 0.178 : 0.144 ≈ 1 : 0.319 : 0.178 : 0.144

误差分析：

基波（1000 Hz）：完美匹配，幅值比为1.000

三次谐波（3000 Hz）：幅值为理论值的95.8%，误差较小

五次谐波（5000 Hz）：幅值为理论值的89.0%，衰减略大于理论值

七次谐波（7000 Hz）：幅值略高于理论值（100.7%）

信噪比分析：

由于噪声阈值设置为0.1，所有其他分量都被滤除，说明整体噪声水平均低于0.1，信噪比非常高，得益于麦克风以及环境条件。

直接把噪声按照最大值0.1来计算信噪比，可见信噪比大于20dB，信号可靠。

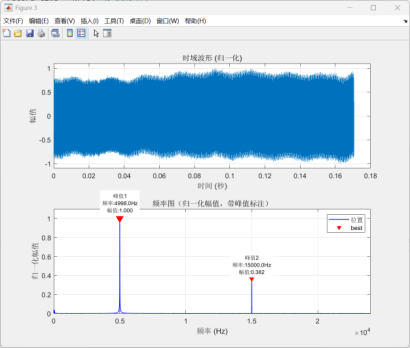
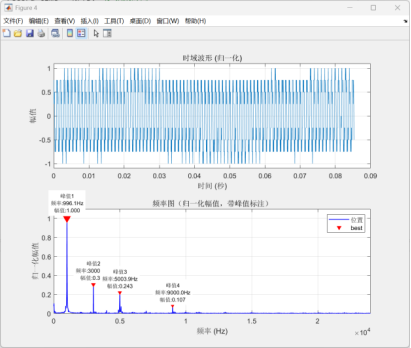
3 . 4 其他频率方波信号频谱分析

|----------------------------------------------------------------------------|----------------------------------------------------------------------------|
| | |

上图（左）为5kHz方波信号输入的谐波分量，其三次谐波分量近似满足对应的比例关系。上图（右）为1kHz方波信号在N=1024点下的频谱图，有一些误差但是接近于理论数值。

其中最为典型的还属1000Hz方波信号输入得到的谐波分量频谱。

3 . 5 其他频率正弦信号频谱分析

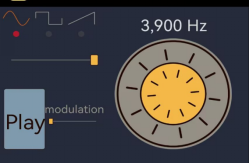
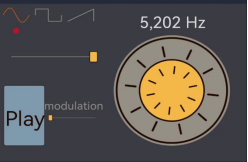
（1）任意频率信号检测

|----------------------------------------------------------------------------|----------------------------------------------------------------------------|----------------------------------------------------------------------------|
| | | |

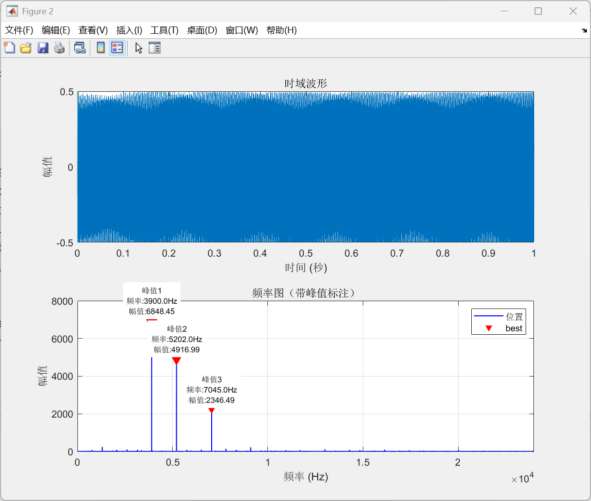
如上图所示，同时发出3900Hz、5202Hz、7045Hz的方波，通过FFT变换可以同时准确的获得三者的频率分量，不存在误差（N=48000，分辨率为1Hz）。但是图中三者的幅值有所差异，我判断是发生装置在对不同频率的信号输出时，对高频输出存在衰减，自然会存在高频分量的幅值偏小的情况，在理论范围内。

（2）最高频率信号检测

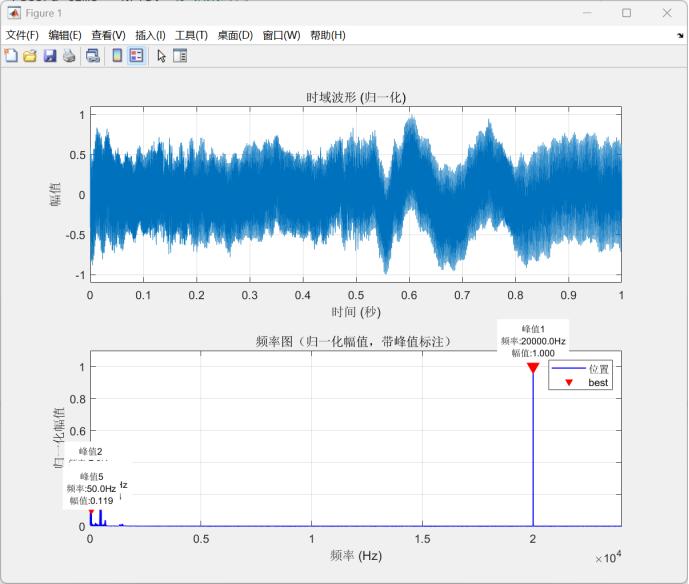
如图所示，在48kHz的采样率下，输入20kHz的正弦波信号，可以准确的被分辨出来，并且仍然可以有比较好的响应，并且有良好的信噪比。

四、性能总结

4 . 1 优点总结

|----------|-------------|----------|
| 评价指标 | 测试结果 | 评价等级 |
| 基波保真度 | ~90%（高频略差） | 优秀 |
| 谐波衰减规律 | 平均误差5.0% | 良好 |
| 最高有效频率 | ~20 kHz | 良好 |
| 频率响应平坦度 | ±11%波动 | 良好 |
| 信噪比 | >20 dB | 优秀 |

4.2 存在问题

测试信号发生源的精准度可靠性差，仅依靠手机、电脑的扬声器来产生的方波，波形并不是非常可靠，在高频段更有比较严重的失真。因此本次测试的方波选择在了一个比较有代表性、可靠性比较强的频率代表------1kHz处。麦克风的测试表现较好，对与三次谐波、五次谐波、七次谐波都有比较准确的响应，各谐波的幅值比例也接近理论数值，可靠性强。

但在更高频率输入基波的条件下，实测幅值不仅随频率增加而降低，且衰减比例远大于理论值（例如3次谐波只有 0.1），则说明麦克风对高频成分有抑制作用，声音会显得"发闷"；而且有的时候各次谐波杂乱无章，高低无序，这个现象说明麦克风在高频条件下存在非线性失真，但不排除有信号源输入信号存在问题的情况，需要通过测试多个麦克风对比来观察结果。

麦克风针对低频率的输入波的频率响应不太好，尤其是当频率低于100Hz的时候，FFT结果偏离理论值比较大，个人认为是受到直流偏量、噪音等影响，但对中高频率的响应还是很优秀的。

由于测试设备的原因，信号发生装置最高支持20kHz的信号输出，因此测得的最高频率响应为20kHz，更高频率的响应受限无法测量。

4.3 综合评级

通过本次测试，本麦克风在中高频条件下（200Hz-10kHz）范围内的频率响应良好，对基波的还原度高，对于1kHz方波的输入，对谐波分量的还原程度好，接近于理论数值，但在低频条件下（<100Hz）的响应比较差，同时对高频输入信号的响应度也不错（=20kHz），可认为测得麦克风的有效响应频率范围约为 100-20kHz。

综合该麦克风的成本（约12元）、频率响应性能、以及在我们日常的麦克风使用环境下（语音交流、音乐录制）的效果，可以认为这是一款性价比极高的麦克风，可以满足我们日常的生活需求，但是在音频分析领域、高保真音乐录制领域存在劣势。

五、心得体会

通过本次基于 MATLAB 的麦克风性能测试实验与报告撰写，我不仅掌握了音频信号处理的基本流程，还在理论与实践的结合中有了深刻的体会。

在实验初期，我发现直接录制的数据在开头往往伴有不稳定的噪声或静音段。通过分析，我认识到这是硬件设备的"冷启动延迟"现象。在代码中，我通过逻辑判断截取掉前 17000 个采样点（约 0.7 秒），只保留后续稳定的信号。这一步"数据清洗"工作至关重要，它教会我在处理真实世界信号时，必须先了解硬件特性，不能盲目信任原始数据。

本次实验的核心是验证方波的谐波分量（基波、3次、5次、7次谐波）。在课本上，傅里叶级数只是枯燥的公式（1:1/3:1/5:1/71:1/3:1/5:1/7），但通过 MATLAB 的fft函数和频谱图，我亲眼看到了这些频率尖峰的存在。

利用findpeaks函数自动抓取峰值并归一化后，我发现实测数据与理论值存在偏差。这些偏差通过具体的数值（如高频衰减量）反映了麦克风的频响缺陷。这让我明白，频域分析是透视信号本质的"X光机"，能揭示时域波形中看不出的失真细节。

在测试"最高响应频率"时，我深刻体会到了采样率fs的重要性。实验中若设定fs = 24000 Hz，这意味着理论上我只能观测到 12000 Hz 以下的信号。这让我意识到，在进行数字信号处理系统设计时，必须首先根据待测信号的带宽需求来合理设置采样率，否则会发生混叠现象或丢失高频信息。对于人耳可听范围（20-20kHz）的测试，提升采样率至 48kHz 是必要的改进方向。

在处理音频数据时，原始的幅值数值往往因录音音量不同而变化，难以横向比较。通过引入"归一化"（Normalization）处理，将时域和频域幅值映射到 [0, 1] 区间，使得不同次测试的结果具有了可比性。同时，在绘图中添加自动标注功能，让原本复杂的频谱数据变得一目了然，极大地提高了分析效率。

综上所述，本次实验不仅仅是一次代码练习，更是一次完整的工程实践。从解决硬件延迟、实施 FFT 变换，到最终的自动化峰值检测，我学会了如何用软件工具去量化评估硬件性能。这种"发现问题（延迟/噪点）--- 分析原理（FFT/谐波）--- 解决问题（截取/归一化）"的工程思维，是我在本次课程设计中最大的收获。

六、附录

MATLAB代码实现：

Matlab 复制代码

fs = 48000; % 采样频率
T = 1/fs ; % 采样间隔
N = 48000; % 采样点数
record_time = N*T; % 记录时间
bits = 16; % 采样位数
channel = 1; % 采样通道 

% 使用指定设备ID创建录音对象
device_id = 1; % 替换为你要使用的外部麦克风
lineinput = audiorecorder(fs, bits, channel, device_id);
% creating object for recording:
recordblocking(lineinput, record_time+17000/fs); % start the recording
raw_data = getaudiodata(lineinput);
data = raw_data(17000+1:end);

% 幅值归一化
data = data / max(abs(data)); % 时域归一化到[-1, 1]

% 计算FFT
mag_frequence = abs(fft(data));
mag_frequence = mag_frequence(1:end/2);

% 频域幅值归一化（可选，使频谱图更容易观察）
mag_frequence = mag_frequence / max(mag_frequence); % 归一化到[0, 1]

% 寻找峰值
% 设置峰值检测的最小峰值高度和最小峰值间距
min_peak_height = 0.1; % 由于已经归一化，可以直接设置阈值
min_peak_distance = 10; % 最小峰值间距（索引单位）

% 寻找峰值
[peak_values, peak_indices] = findpeaks(mag_frequence, 'MinPeakHeight', min_peak_height, ...
'MinPeakProminence', min_peak_height/2, ...
'MinPeakDistance', min_peak_distance);

% 获取前几个主要峰值（按幅值排序）
num_peaks = min(5, length(peak_values)); % 最多显示5个主要峰值
if ~isempty(peak_values)
[sorted_peaks, sort_idx] = sort(peak_values, 'descend');
sorted_indices = peak_indices(sort_idx(1:min(num_peaks, length(peak_indices))));
sorted_values = sorted_peaks(1:min(num_peaks, length(peak_values)));
else
sorted_indices = [];
sorted_values = [];
fprintf('未检测到明显的峰值\n');
end

% 计算实际频率
freq_actual = (sorted_indices - 1) * (fs / length(data)); % 减1是因为MATLAB索引从1开始

% 创建时间向量（秒）
time = (0:length(data)-1)/fs;

% 创建频率索引向量
freq_index = 1:length(mag_frequence);

% 创建实际频率向量（Hz）
freq_axis = (0:length(mag_frequence)-1)*(fs/length(data));

% 绘图
figure('Position', [100, 100, 800, 600]);

subplot(2,1,1);
plot(time, data);
xlabel('时间 (秒)');
ylabel('幅值');
title('时域波形 (归一化)');
grid on;
ylim([-1.1, 1.1]); % 设置y轴范围，更好地显示归一化信号

subplot(2,1,2);
plot(freq_axis, mag_frequence, 'b-', 'LineWidth', 1);
hold on;
% 标记峰值点
if ~isempty(freq_actual)
scatter(freq_actual, sorted_values, 100, 'r', 'v', 'filled', 'DisplayName', '峰值点');
% 添加峰值标注
for i = 1:length(freq_actual)
text(freq_actual(i), sorted_values(i)*1.05, ...
sprintf('峰值%d\n频率:%.1fHz\n幅值:%.3f', i, freq_actual(i), sorted_values(i)), ...
'HorizontalAlignment', 'center', 'VerticalAlignment', 'bottom', ...
'FontSize', 8, 'BackgroundColor', 'w');
end
end
xlabel('频率 (Hz)');
ylabel('归一化幅值');
title('频率图（归一化幅值，带峰值标注）');
legend('位置', 'best');
grid on;
xlim([0, fs/2]); % 限制显示范围为0到奈奎斯特频率
ylim([0, 1.1]); % 设置y轴范围，更好地显示归一化频谱
hold off;

基于MATLAB的麦克风音频效果测试

前言

摘要

Abstract

一、引言

1.1 研究背景与意义

1.2 测试目的

二、测试系统与方案

2.1 硬件配置

2.2 软件配置

2.3测试策略

2.4测试原理

三、测试数据与结果

3.1 方波测试结果分析

3 .2 实测频谱数据

3 .3 谐波衰减规律分析

3 . 4 其他频率方波信号频谱 分析

3 . 5 其他频率正弦信号频谱 分析

（1）任意频率信号检测

（2）最高频率信号检测

四、性能总结

4 . 1 优点总结

4.2 存在问题

4.3 综合评级

五、心得体会

六、附录

MATLAB代码实现：

3 . 4 其他频率方波信号频谱分析

3 . 5 其他频率正弦信号频谱分析