【微实验】从声波涟漪到频率栅栏：梳状滤波的声学奥秘与工程启示

目录

[01 序章：厅堂中的回声暗语](#01 序章：厅堂中的回声暗语)

[02 数学之舞：时延如何编织频率栅栏](#02 数学之舞：时延如何编织频率栅栏)

[03 声学实践：从问题到解决方案](#03 声学实践：从问题到解决方案)

[04 技术启示：从理解到驯服](#04 技术启示：从理解到驯服)

[05 跨界联想：波动世界的共同语言](#05 跨界联想：波动世界的共同语言)

当你在音乐厅聆听交响乐时，每个乐器声音都经由复杂的路径抵达耳朵，但你是否知道，那些看似寻常的延时和叠加，正悄然编织着一张精密的频率筛网？

清晨的第一缕阳光透过百叶窗，在地板上投下明暗交替的光带------这是一种"光学梳状滤波"，光的波动性在狭缝间发生干涉，形成规则的亮暗条纹。

声波的世界里，同样上演着类似的故事。当直达声与延时反射声在空中相遇，它们不是简单叠加，而是在某些频率上相互抵消，在另一些频率上相互增强，形成一张看不见的"声学栅栏"。

---

01 序章：厅堂中的回声暗语

在声学领域，梳状滤波是一个无处不在却又常被忽略的现象。想象一下，在一个铺满瓷砖的卫生间里唱歌，你会听到自己的声音变得"空洞"而"金属感"------这就是早期反射声与直达声干涉的结果。

两个波形相同但存在微小时间差的声波叠加时，它们在某些频率上同相相加（增强），在某些频率上反相相消（减弱）。这种增强和减弱在频率轴上呈现规律的周期性间隔，就像一把梳子的齿状结构，因而得名"梳状滤波"。

为何这个现象如此重要？因为它直接影响着我们对声音的感知。在录音棚中，它可能导致某些音符神秘消失；在会议系统里，它会让语音清晰度大打折扣；而在音乐厅设计中，巧妙利用它则可以塑造独特的空间感。

---

02 数学之舞：时延如何编织频率栅栏

梳状滤波的核心数学关系简洁而优美，只需一个基本公式便能揭示其时域与频域的深刻联系：

H(f) = 1 + α·e^{-j2πfτ}

其中，α是延时信号的相对幅度（0<α≤1），τ是延时时间（秒），f是频率（Hz）。这个传递函数的幅度响应为：

|H(f)| = √[1 + α² + 2α·cos(2πfτ)]

这一简洁的表达式蕴含着丰富的声学现象：

• 周期性零点 ：当cos(2πfτ) = -1且α=1时，传递函数为零，声音完全抵消

• 周期性峰值 ：当cos(2πfτ) = 1时，传递函数达到最大值(1+α)

• 峰谷间隔 ：峰值频率间隔为1/τHz，谷值频率间隔为1/(2τ)Hz

这个数学模型如同一位精密的织布工，用时间差τ作为梭子，在频率轴上编织出规则的花纹。5毫秒的延时（τ=0.005s）会产生峰谷间隔200Hz的梳状结构------这正是许多室内声学问题的典型特征。

下面的可视化展示了不同参数下梳状滤波响应的变化规律：

三条曲线揭示了参数变化的明确规律：

• 延时τ是梳齿密度的编织者：τ增大（红→蓝线），峰谷频率间隔减半（从200Hz→100Hz），梳齿更密集

• 衰减α是峰谷深度的雕刻师：α增大（红→绿线），谷值更深（-15dB→-20dB），声染色更明显

• 参数组合产生复杂变异：同时调整两者（红线→紫线），形成密集且深陷的梳状结构

---

03 声学实践：从问题到解决方案

在现实声学工程中，梳状滤波既是挑战也是工具。录音棚的多话筒设置 中，若两个话筒以不同距离录制同一音源，必然引入时间差，产生梳状滤波效应。同样，音箱阵列的安装若未精确计算各单元到达听音点的时延，也会在覆盖区域产生频率响应凹陷。

语音识别系统在嘈杂环境下面临的回声干扰问题，本质上也是梳状滤波的一种表现。早期反射声与直达声的干涉会导致某些语音频率成分被削弱，降低识别准确率。

%% 梳状滤波效应可视化：主话筒+环境话筒（叠加vs分离）
% 增强版本：添加动态频谱分析
clc; clear; close all;

%% 步骤1：设置核心参数
Fs = 44100;            % 采样率（音频标准44.1kHz）
t_total = 1;           % 信号总时长（1秒）
t = 0:1/Fs:t_total-1/Fs; % 时间轴
tau = 0.005;           % 环境话筒相对主话筒的延时（5毫秒）
amp_env = 0.8;         % 环境话筒信号振幅衰减

%% 步骤2：生成模拟主话筒信号（多频率成分，更真实）
f0 = 440;              % 基频
f1 = 880;              % 倍频
f2 = 1320;             % 三倍频
f3 = 1760;             % 四倍频

% 包含多个频率成分的主话筒信号
main_mic = 0.5*sin(2*pi*f0*t) + ...
           0.3*sin(2*pi*f1*t) + ...
           0.2*sin(2*pi*f2*t) + ...
           0.1*sin(2*pi*f3*t) + ...
           0.05*randn(size(t));

%% 步骤3：生成模拟环境话筒信号（带延时）
delay_samples = round(tau * Fs);  % 延时对应的采样点数
env_mic = zeros(size(t));
env_mic(delay_samples+1:end) = amp_env * main_mic(1:end-delay_samples);

%% 步骤4：创建叠加信号和分离信号
mix_mic = main_mic + env_mic;  % 信号叠加

% 分离信号（立体声）
sep_signal = zeros(length(t), 2);
sep_signal(:, 1) = main_mic;      % 主话筒→左声道
sep_signal(:, 2) = env_mic;       % 环境话筒→右声道

%% 步骤5：动态频谱分析
window_size = 1024;          % 窗口大小
overlap = 512;               % 重叠采样点数
nfft = 1024;                 % FFT点数

% 计算滑动窗口频谱
[mix_spectrogram, F_mix, T_mix] = spectrogram(mix_mic, hamming(window_size), overlap, nfft, Fs);
[main_spectrogram, F_main, T_main] = spectrogram(main_mic, hamming(window_size), overlap, nfft, Fs);

% 转换为分贝
mix_spectrogram_db = 20*log10(abs(mix_spectrogram) + eps);
main_spectrogram_db = 20*log10(abs(main_spectrogram) + eps);

%% 步骤6：核心可视化 - 梳状滤波效应展示
figure('Position', [100, 100, 1400, 900]);

% 子图1：信号波形对比
subplot(3, 3, [1, 2]);
plot(t, main_mic, 'b', 'LineWidth', 1.5, 'DisplayName', '主话筒信号');
hold on;
plot(t, env_mic, 'g', 'LineWidth', 1.5, 'DisplayName', '环境话筒信号');
plot(t, mix_mic, 'r', 'LineWidth', 1.5, 'DisplayName', '叠加信号');
xlabel('时间 / s');
ylabel('振幅');
title('信号波形对比（前100ms）');
xlim([0, 0.1]);
legend('Location', 'best');
grid on;

% 子图2：梳状滤波频谱理论曲线
subplot(3, 3, 3);
f_theory = linspace(0, 5000, 1000);
comb_filter_response = 1 + amp_env^2 + 2*amp_env*cos(2*pi*f_theory*tau);
plot(f_theory, 10*log10(comb_filter_response), 'k-', 'LineWidth', 2);
xlabel('频率 / Hz');
ylabel('幅度 / dB');
title('梳状滤波器理论响应');
xlim([0, 2000]);
grid on;

% 标记梳状滤波的峰谷频率
hold on;
peak_freq = (0:1/tau)/2;  % 峰值频率
null_freq = (1:2:1/tau)/(2*tau); % 谷值频率
for i = 1:min(10, length(peak_freq))
    if peak_freq(i) <= 5000
        plot([peak_freq(i), peak_freq(i)], [-20, 10], 'r:', 'LineWidth', 0.5);
        text(peak_freq(i), 12, sprintf('峰\n%.0fHz', peak_freq(i)), ...
            'HorizontalAlignment', 'center', 'FontSize', 8);
    end
end
for i = 1:min(10, length(null_freq))
    if null_freq(i) <= 5000
plot([null_freq(i), null_freq(i)], [-20, 10], 'b:', 'LineWidth', 0.5);        text(null_freq(i), -25, sprintf('谷\n%.0fHz', null_freq(i)), ...
            'HorizontalAlignment', 'center', 'FontSize', 8);
    end
end

% 子图3：叠加信号时频图（谱图）
subplot(3, 3, 4);
imagesc(T_mix, F_mix, mix_spectrogram_db);
axis xy;
xlabel('时间 / s');
ylabel('频率 / Hz');
title('叠加信号时频图（梳状滤波效应）');
colorbar;
caxis([-40, 20]);
ylim([0, 5000]);

% 子图4：主信号时频图对比
subplot(3, 3, 5);
imagesc(T_main, F_main, main_spectrogram_db);
axis xy;
xlabel('时间 / s');
ylabel('频率 / Hz');
title('主信号时频图（无梳状滤波）');
colorbar;
caxis([-40, 20]);
ylim([0, 5000]);

% 子图5：分离信号波形
subplot(3, 3, 6);
plot(t, sep_signal(:,1), 'b', 'LineWidth', 1.5, 'DisplayName', '左声道（主话筒）');
hold on;
plot(t, sep_signal(:,2), 'g', 'LineWidth', 1.5, 'DisplayName', '右声道（环境话筒）');
xlabel('时间 / s');
ylabel('振幅');
title('分离信号波形（前50ms）');
xlim([0, 0.05]);
legend('Location', 'best');
grid on;

% 子图6：频域对比 - 主要频率成分分析
subplot(3, 3, [7, 9]);
% 计算整体频谱
[Pxx_mix, F_mix_full] = pwelch(mix_mic, hamming(4096), 2048, 4096, Fs);
[Pxx_main, F_main_full] = pwelch(main_mic, hamming(4096), 2048, 4096, Fs);

plot(F_mix_full, 10*log10(Pxx_mix), 'r-', 'LineWidth', 1.5, 'DisplayName', '叠加信号');
hold on;
plot(F_main_full, 10*log10(Pxx_main), 'b-', 'LineWidth', 1.5, 'DisplayName', '主信号');
xlabel('频率 / Hz');
ylabel('功率谱密度 / dB');
title('频域对比：梳状滤波对频谱的影响');
xlim([0, 2500]);
legend('Location', 'best');
grid on;

% 标记主要频率成分的增强/减弱
freqs = [f0, f1, f2, f3];
colors = {'r', 'g', 'b', 'm'};
for i = 1:length(freqs)
    % 找到最近频率点
    [~, idx_mix] = min(abs(F_mix_full - freqs(i)));
    [~, idx_main] = min(abs(F_main_full - freqs(i)));
    
    % 绘制连接线
    plot([freqs(i), freqs(i)], ...
         [10*log10(Pxx_main(idx_main)), 10*log10(Pxx_mix(idx_mix))], ...
         [colors{i}, '--'], 'LineWidth', 1);
    
    % 标注变化量
    change = 10*log10(Pxx_mix(idx_mix)/Pxx_main(idx_main));
    text(freqs(i), 10*log10(Pxx_mix(idx_mix)) + 3, ...
        sprintf('%+.1f dB', change), ...
        'HorizontalAlignment', 'center', 'FontSize', 9, 'Color', colors{i});
end

% 添加总标题
sgtitle('梳状滤波效应全面分析：理论、时域与频域表现');

%% 步骤7：参数影响交互式探索（简化版）
fprintf('\n梳状滤波关键参数：\n');
fprintf('延时 τ = %.3f 秒 (%.1f 毫秒)\n', tau, tau*1000);
fprintf('衰减系数 α = %.2f\n', amp_env);
fprintf('峰值频率间隔 = %.1f Hz\n', 1/tau);
fprintf('谷值频率间隔 = %.1f Hz\n', 1/(2*tau));

% 显示主要频率点的变化
fprintf('\n主要频率点振幅变化：\n');
for i = 1:length(freqs)
    f = freqs(i);
    theoretical_change = 10*log10(1 + amp_env^2 + 2*amp_env*cos(2*pi*f*tau));
    fprintf('  %.0f Hz: %+.2f dB (理论值)\n', f, theoretical_change);
end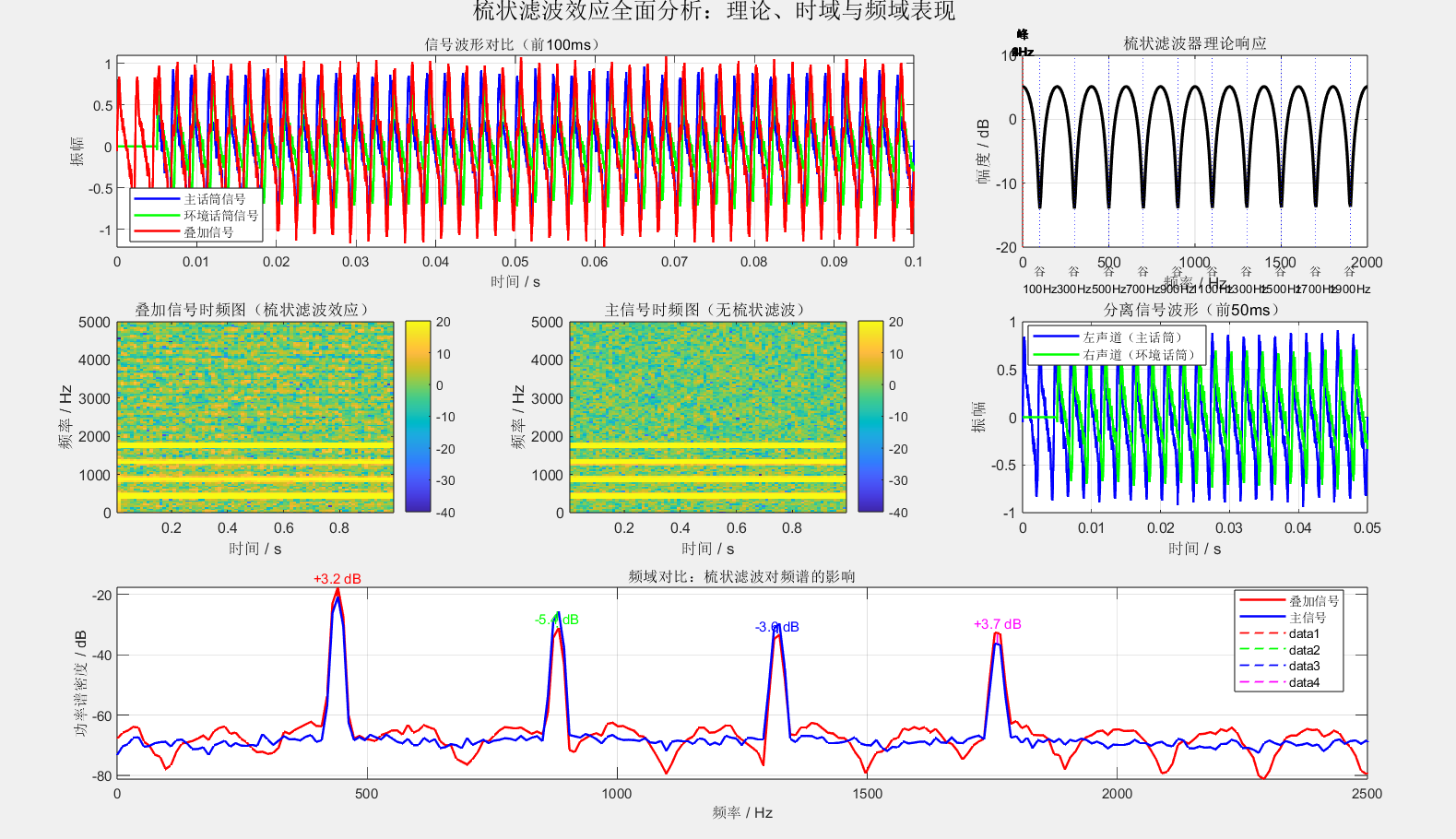

这段代码通过完整的可视化分析，展示了梳状滤波如何在时域和频域影响声音信号。运行后将生成包含六个子图的综合分析界面，清晰展示：

1. 时域波形叠加效果

2. 理论梳状滤波响应曲线（明确标出峰谷频率）

3. 叠加信号的时频图（揭示随时间变化的频率结构）

4. 原始信号的时频图对比

5. 分离信号的多声道波形

6. 频域详细对比分析（量化主要频率成分的变化）

---

04 技术启示：从理解到驯服

理解梳状滤波的机制为声学设计提供了多种创新思路。数字延迟线技术允许我们精确控制延时量，从而将有害的梳状滤波转化为创造性的声音效果。许多数字混响效果器正是基于这一原理，通过多抽头延迟线模拟不同反射路径。

自适应滤波算法能够实时识别并抵消特定的梳状滤波模式，这在会议系统和助听器中尤为重要。通过不断调整滤波参数，系统可以最小化房间反射带来的负面影响，提高语音清晰度。

在音乐制作领域，梳状滤波已被创造性应用为一种独特的音色塑造工具。通过精细调整延时时间和反馈量，制作人可以创造出从绵长混响到金属感共鸣的各种效果。

---

05 跨界联想：波动世界的共同语言

梳状滤波的本质是波的干涉现象，这一原理在物理学各个领域都有体现。光学中的薄膜干涉正是梳状滤波的"光版本"，肥皂泡上绚丽的色彩、相机镜头上的增透膜，都基于相同的干涉原理。

在无线电通信领域，多径效应导致的信号衰落与梳状滤波有着相同的数学模型。无线信号经过不同路径到达接收器，产生时延导致某些频率成分相互抵消，形成频率选择性的衰落。

甚至量子力学中的物质波干涉也能用类似框架理解。当粒子波函数通过不同路径后重新组合，也会产生类似梳状滤波的概率分布模式。

这种跨领域的相通性提示我们，梳状滤波不仅是一个声学或信号处理概念，更是理解波动现象的统一视角。它连接了声学、光学、通信和量子物理，展现了自然规律的简洁与统一。

当我们再次走进一个声学空间，聆听其中的声音时，或许能感知到那些无形的频率栅栏正在如何塑造我们的听觉体验。从问题到工具，从挑战到创意，梳状滤波的故事告诉我们：深刻理解自然现象的内在规律，总能让我们找到与之共处甚至善用之道。

那些看似干扰我们感知的"瑕疵"，当被充分理解后，往往能转化为创造新体验的源泉------这或许就是科学与艺术相遇时，最动人的时刻。