买卖股票问题

本文将介绍六道买卖股票问题从易到难，用到了贪心算法以及动态规划算法。

第一题：一次交易

思路：这道题我们只能有一次买卖机会，所以我们可以找出价格最低的这天买，然后在后面的日期找出价格最高的卖出，使用一个变量来记录前缀的最小值，然后用 i 遍历这个数组，每次求出 i 位置的值和前缀最小值之间的差，用来更新结果 ret ，ret每次更新为旧的 ret 和本次差值的最大值

我们用第一个例子来模拟这个过程：

先把前缀变量初始化为最大值，ret初始化为0，i从数组第一个位置遍历：

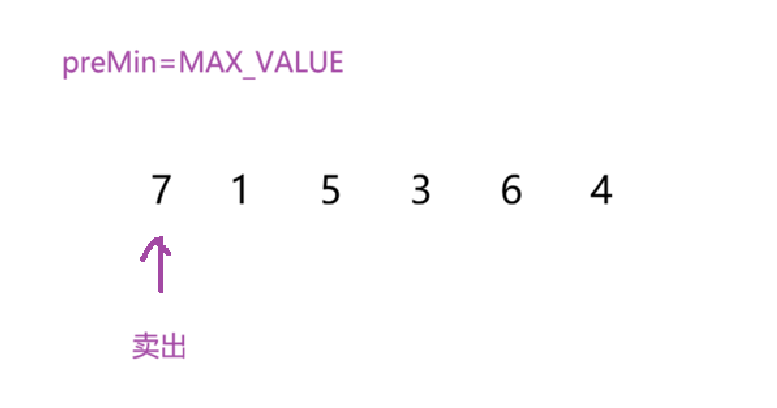
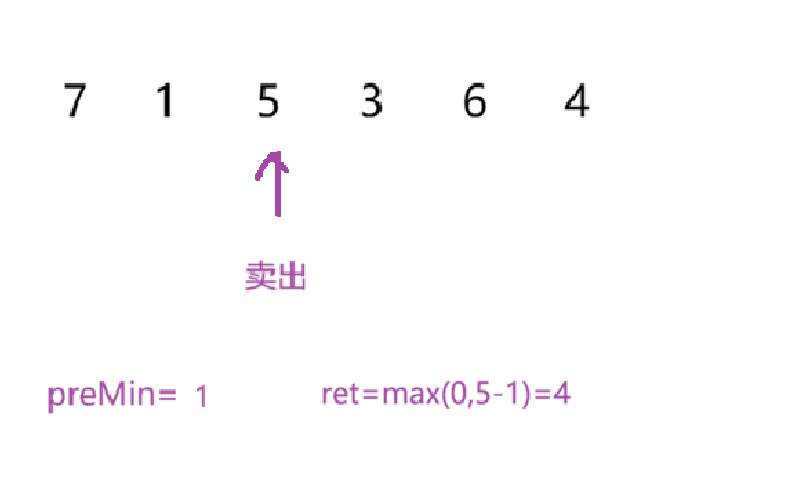
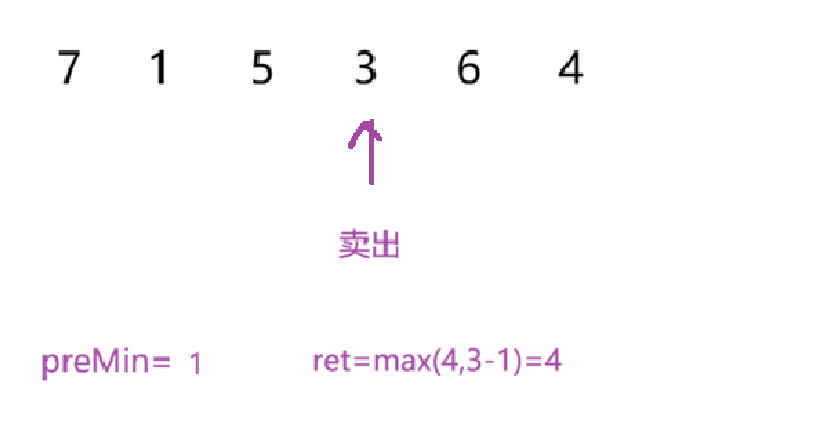
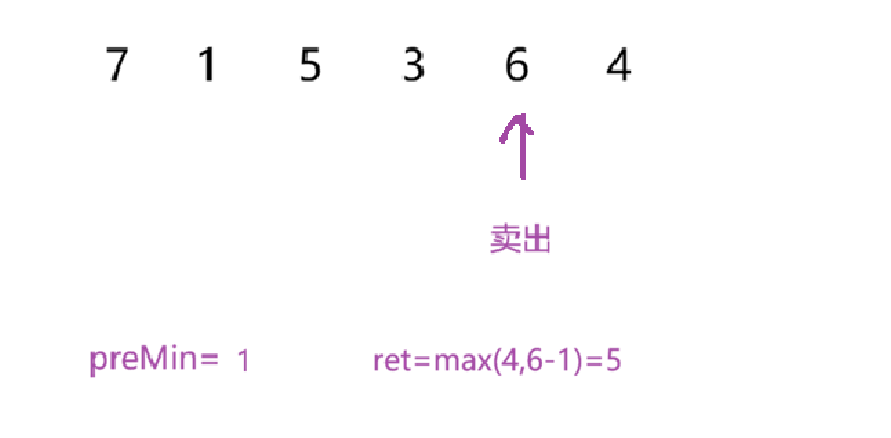
根据以上过程，我们来看代码：

class Solution {
    //本题使用贪心解法+变量标记最小值
    public int maxProfit(int[] prices) {
        int preMin=Integer.MAX_VALUE;//将preMin先初始化为最大值
        int ret=0;
        for(int i=0;i<prices.length;i++){
            //先更新结果然后更新最小值(prices[i]表示卖出股票的日期)
            ret=Math.max(ret,prices[i]-preMin);//更新为最大利润
            //更新最小值，当i移动到下一个位置的时候，要算前面一堆的最小值，只需要求出现在preMin和i这个位置对应的值的最小值
            //因为preMin里面存的就已经是当前i前面这些值里面的最小值了
            preMin=Math.min(preMin,prices[i]);
        }
        return ret;
    }
}

第二题：多次交易

本道题和前一道不同的是：我们可以多次进行买卖，实际上就是在这个数组里面，我们找出所有递增的子序列，然后求出每一段的差值，最后把结果相加即可。

核心思路是双指针：用 i 来找出每段递增子序列的最小值，用 j 来找出每段递增子序列的最大值。

具体过程如下图，我们先把价格的变化绘制在坐标系中：

让i从数组第一个位置开始，让j从i的位置开始向后寻找

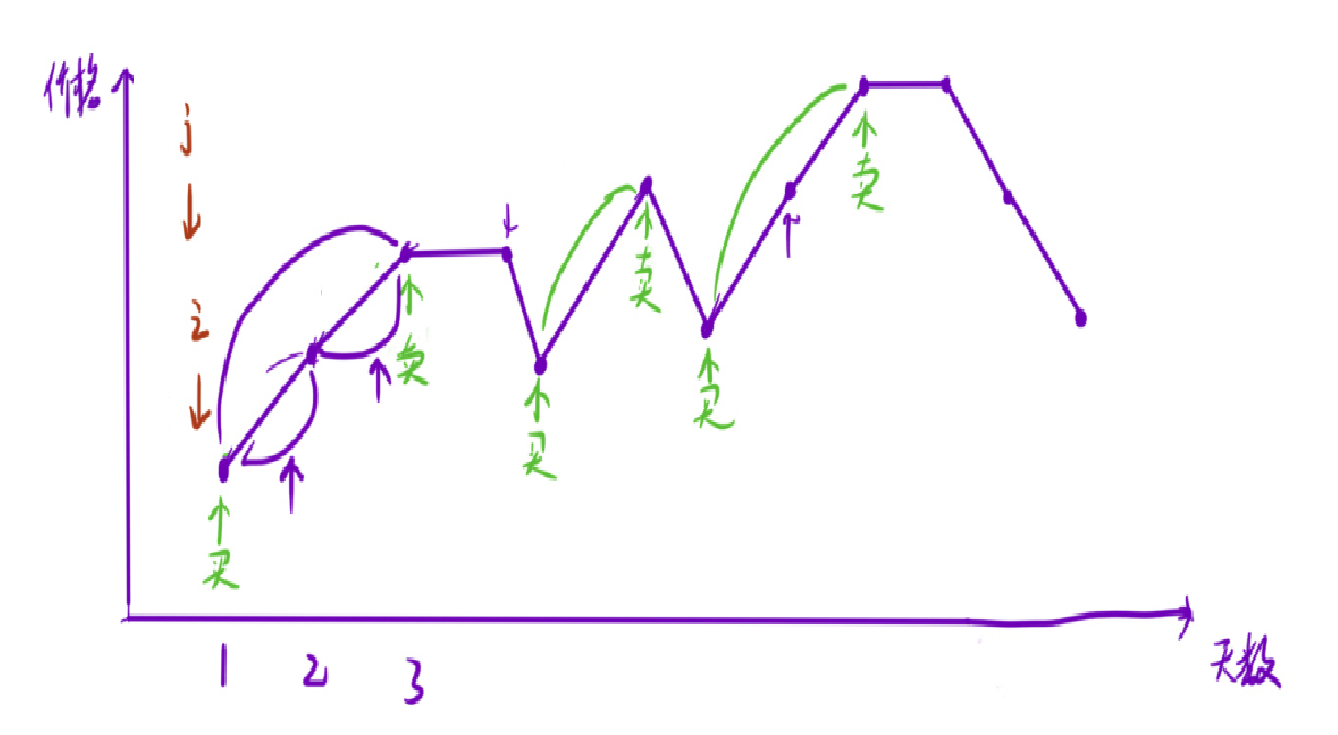
当 j 后面的数不大于此时 j 位置的数时，说明我们找到了第一个递增的序列，然后更新

ret+=nums[j]-nums[i]

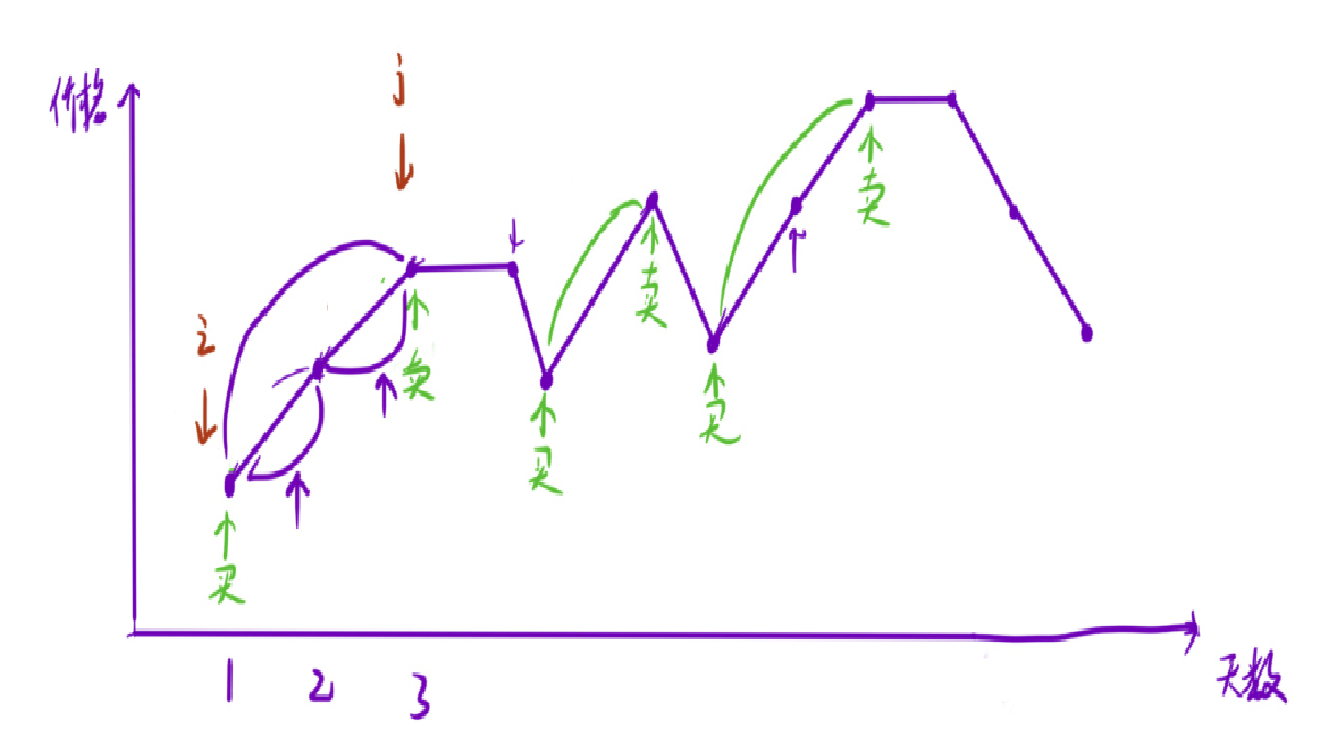
然后我们让 i 走到 j 的下一个位置

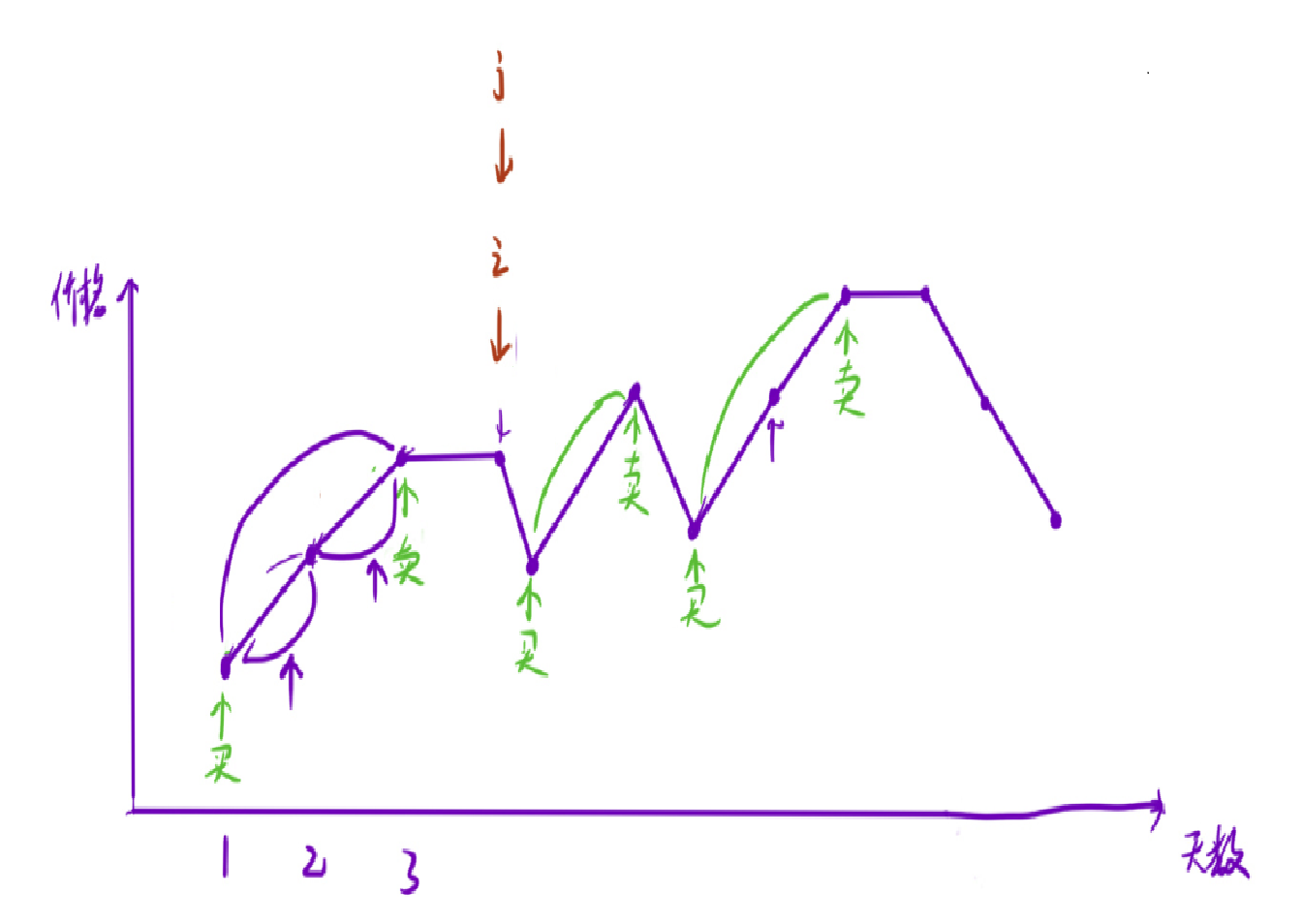
这时 j 后面的数小于当前 j 位置的数，所以更新ret (相当于+0)，然后 i 移动到 j 的下一个位置，j从i的位置又开始向后寻找，找到第二个递增的序列，然后继续更新结果

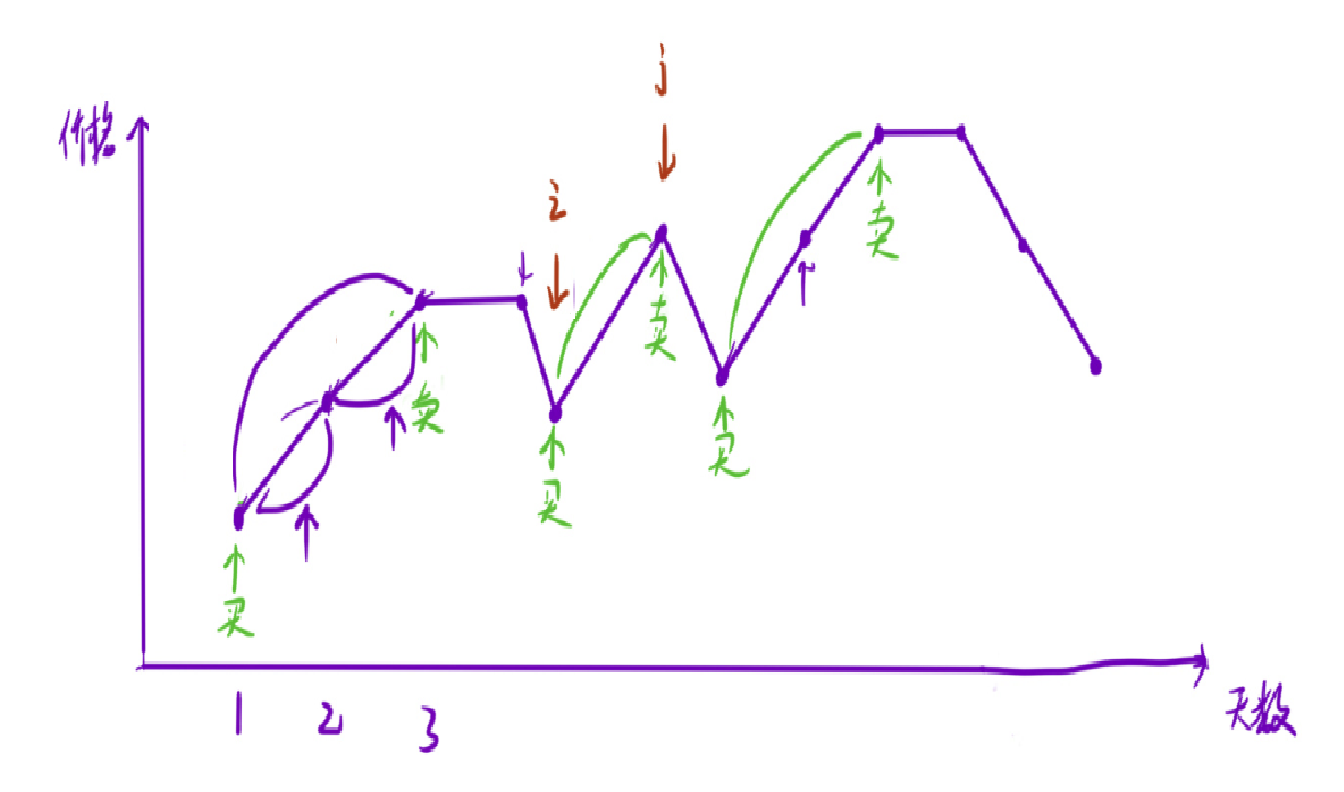
后面的过程我们不在放图片，接下来可以编写代码：

注意while循环的条件是 j+1<n ，因为每次要判断后一个位置和当前 j 位置值大小

class Solution {
    //本道题实质是在一段序列里面找出递增的子序列，然后把递增的差值结果相加
    public int maxProfit(int[] prices) {
        int ret=0;
        int n=prices.length;
        for(int i=0;i<n;i++){
            int j=i;//让j从i的位置向后移动，找到这个阶段递增的最大值
            while(j+1<n && prices[j]<prices[j+1]){
                j++;
            }
            //到这里说明j移动到了这个阶段递增的最大位置
            //如果出现j和i位置值相等的话，这个阶段的ret=0也不影响最终结果
            ret+=prices[j]-prices[i];
            //然后让i移动到j的下一个位置，继续重复上述的过程
            //但是这里有个问题，for循环中有i++,所以我们这里让i=j即可
            i=j;
        }
        return ret;  
    }
}

第三题：含有冷冻期

本道题增加了一个限制，在卖出股票之后会有一天的冷冻期，这时我们不能进行购买股票，本道题我们采用动态规划的方法来解决。核心思路就是状态定义与拆分。

1、状态表示：

我们定义 dp[i][j] 表示第**i** 天结束后，处于状态**j** 时的最大利润，其中 **j**分为三类：

j=0（买入 / 持有状态） ：第 i 天结束时持有股票。（第i天买的股票）

j=1（可交易状态） ：第 i 天结束时不持有股票，且不在冷冻期（可以随时买入）。（第i天要么"躺平"，要么刚过了冷冻期）

j=2（冷冻期状态） ：第 i 天结束时不持有股票，且是当天刚卖出（次日不能买入）。（第i天卖了股票）

2、状态转移方程：

dp[i][0]:

（1）第 i-1 天已经持有，第 i 天不操作 → 利润为 dp[i-1][0]。

（2）第 i-1 天处于 "可交易" 状态（否则无法买入，冷冻期不能买），第 i 天买入 → 利润为 dp[i-1][1] - prices[i]（买入花钱，利润减少）

求出两种情况的最大值即可

dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] - prices[i])

dp[i][1]:

（1）第 i-1 天已经是可交易状态，第 i 天不操作 → 利润为 dp[i-1][1]

（2）第 i-1 天结束进入 "冷冻期"，第 i 天冷冻期结束，变为可交易 → 利润为 dp[i-1][2]

dp[i][1] = Math.max(dp[i-1][1], dp[i-1][2])

dp[i][2]:

第 i-1 天持有股票，第 i 天卖出，这天结束后进入冷冻期 → 利润为 dp[i-1][0] + prices[i]（卖出赚钱，利润增加）

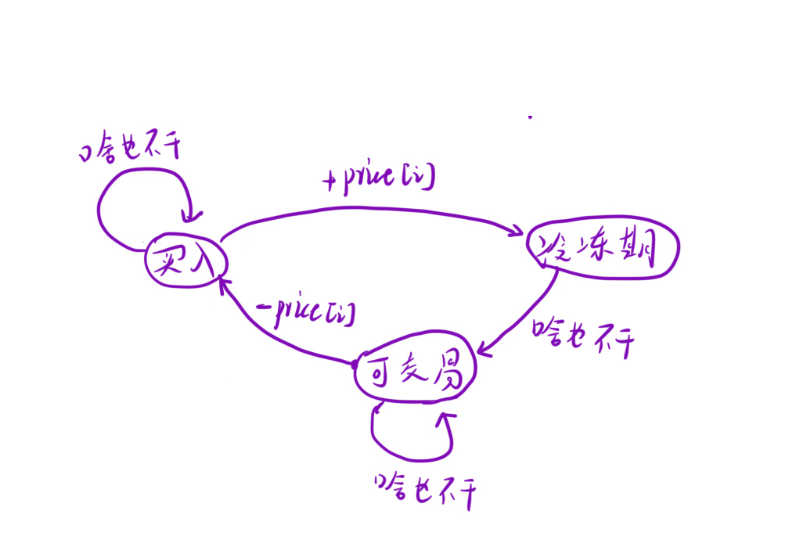
dp[i][2] = dp[i-1][0] + prices[i];

三个状态的转移关系可以用状态机理解：

• 持有（0）→ 冷冻期（2）：卖出操作。
• 可交易（1）→ 持有（0）：买入操作。
• 冷冻期（2）→ 可交易（1）：冷冻期结束。
• 每个状态也可以 "原地踏步"（不操作，延续当前状态）。

3、初始化

dp[0][0] = -prices[0]：第 0 天买入股票，利润为负的股价（花钱买入）。

dp[0][1] = 0：第 0 天不操作，处于可交易状态，利润为 0。

dp[0][2] = 0：第 0 天买了又卖了，因此冷冻期利润为 0。

4、返回值

最后一天结束后，最大利润不可能来自 "持有状态"（因为持有股票未卖出，利润不如卖出），因此只需比较 可交易状态（j=1）和冷冻期状态（j=2） 的利润，取最大值：

return Math.max(dp[n-1][1], dp[n-1][2]);

最后我们来看代码编写：

class Solution {
    public int maxProfit(int[] prices) {
        int n=prices.length;
        //创建dp表
        int[][] dp=new int[n][3];
        //初始化,买入的话利润为负数，其他两种状态都为0
        dp[0][0]=-prices[0];
        //填表,i从1开始
        //dp[i][j] 表示第i天结束后，处于j状态
        for(int i=1;i<n;i++){
            //前一天也是买入状态，第i天没操作，或者前一天处于可交易状态，第i天买的
            dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]-prices[i]);
            //前一天也是可交易状态，第i天没操作，或者前一天处于于冷冻期状态，第i天冷冻期结束
            dp[i][1]=Math.max(dp[i-1][1],dp[i-1][2]);
            //前一天是买入状态，第i天卖了
            dp[i][2]=dp[i-1][0]+prices[i];
        }
        return Math.max(dp[n-1][1],dp[n-1][2]);
    }
}

第四题：含有手续费

这道题添加了手续费这里要注意，手续费在一次交易中减掉一次就行，我们统一在卖出状态时减掉手续费

核心解题思路：

1、状态表示：

我们定义两个状态数组，来表示每天结束后的两种状态：

• f[i] ：第 i 天结束后，处于「买入 / 持有股票」状态时的最大利润
• g[i] ：第 i 天结束后，处于「卖出 / 不持有股票」状态时的最大利润

2、状态转移方程：

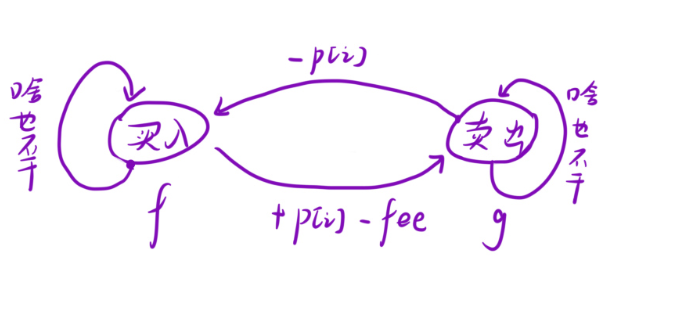
（1）买入状态 f[i]

第 i 天是买入状态，有两种可能的来源：

延续昨天的买入状态 ：昨天已经持有股票，今天继续持有 → 利润为 f[i-1]

昨天不持有，今天买入 ：昨天处于卖出状态，今天买入股票 → 利润为**g[i-1] - prices[i]**

f [ i ]= max( f [ i − 1] , g [ i − 1 ] − prices[ i ] )

（2）卖出状态 g[i]

第 i 天是卖出状态，有两种可能的来源：

延续昨天的卖出状态 ：昨天已经卖出股票，今天继续不持有 → 利润为 g[i-1]

昨天持有，今天卖出 ：昨天处于持有状态，今天卖出股票并支付手续费 → 利润为 f[i-1] + prices[i] - fee（用昨天的利润加上今天的股价，再减去手续费）

因此状态转移方程为：

g [ i ]= max( g [ i − 1] , f [ i − 1 ] + prices[ i ] - fee)

3. 初始化（边界条件）

我们需要定义第 0 天（第一天）的初始状态：

• f[0] = -prices[0]：第 0 天买入股票，利润为负的股价（因为刚买入还没卖出，没有收益）
• g[0] = 0：第 0 天不持有股票，没有任何操作，利润为 0

4、代码实现

class Solution {
    public int maxProfit(int[] prices, int fee) {
        //创建两个dp表表示两种状态
        int n=prices.length;
        int[] f=new int[n]; //买入状态
        int[] g=new int[n]; //卖出状态
        //初始化
        f[0]=-prices[0];g[0]=0;
        //填表
        for(int i=1;i<n;i++){
            //状态转移方程,手续费在买入或者卖出时减掉一次就行
            f[i]=Math.max(f[i-1],g[i-1]-prices[i]);
            g[i]=Math.max(g[i-1],f[i-1]+prices[i]-fee);
        }
        //返回结果，结果一定是卖出状态时获得最大值
        return g[n-1];
    }
}

第五题：最多两次交易

本道题限制了完成的次数最多为两次，所以我们还需要统计一下交易次数，因此可以考虑使用二维dp表来完成这道题

1、状态表示

我们用两个二维数组，把 "天数""交易次数""买入/卖出" 三个信息整合：

• f[i][j] ：第 i 天结束后，完成了 j 次交易，此时处于买入状态下最大利润；
• g[i][j] ：第 i 天结束后，完成了 j 次交易，此时处于卖出状态下最大利润；

2、状态转移方程

在卖出股票后才算完成一次交易

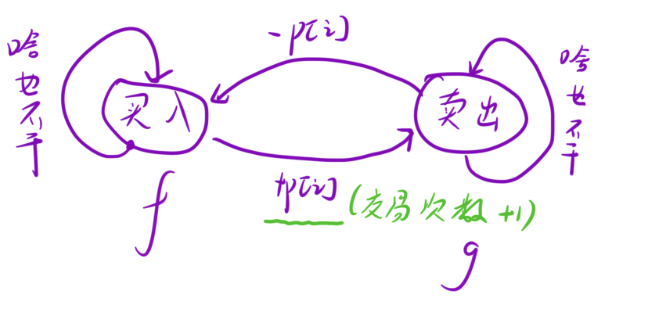
（1）买入状态 f[i][j]

延续昨天的买入状态 ：昨天已经持有股票，今天继续持有 → 利润为 f[i-1][j]

昨天不持有，今天买入 ：昨天处于不持有状态，今天买入股票（买入不增加交易次数，因为交易次数以 "卖出" 为完成标志）→ 利润为 g[i-1][j] - prices[i]

因此状态转移方程：

f[i][j]=max(f[i-1][j] , g[i-1][j]-prices[i])

注意：**g[i-1][j]**这里是j，因为进入买入状态，并不会改变交易次数，只有卖出股票，才算交易次数。

（2）不持有股票状态 g[i][j]

延续昨天的卖出状态 ：昨天已经不持有，今天继续不持有 → 利润为 g[i-1][j]

昨天持有，今天卖出 ：昨天处于持有状态，今天卖出股票（卖出后完成 1 次交易，所以交易次数从 j-1 变成 j）→ 利润为**f[i-1][j-1] + prices[i]**
注意：当 j=0 时，j-1=-1 是无效的（没有负次数的交易），所以这种情况只能选择 "延续不持有"。

因此状态转移方程：

当 j =0 时：

g[i][j]=g[i-1][j]

当 j >0 时：

g[i][j]=max(g[i-1][j] , f[i-1][j-1] + prices[i])

3、 初始化

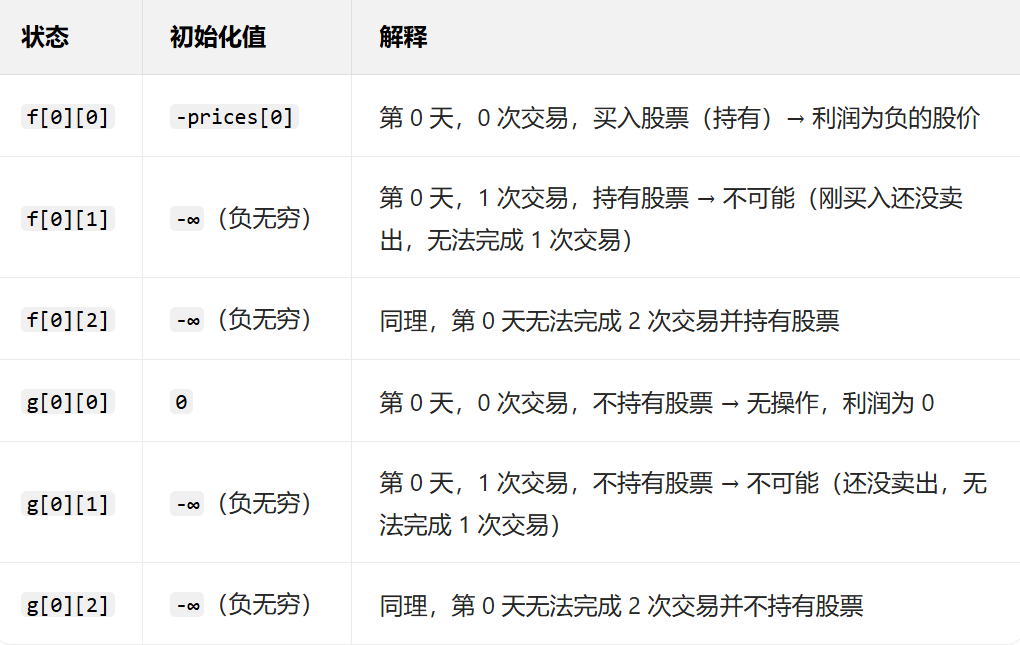
0 （第一天）的状态需要单独初始化，因为没有 "前一天" 可以依赖：

将无法到达的状态初始化为负无穷，防止干扰后续最大值计算

4、返回值

因为最多可以完成 2 次交易，所以我们需要取最后一天（i=n-1）所有不持有状态的最大值：

max( g[n−1][0] , g[n−1][1] , g[n−1][2] )

5、代码编写

class Solution {
    //这道题我们还需要考虑交易次数，交易次数<=2，所以这道题我们需要二维dp表来表示
    public int maxProfit(int[] prices) {
        int n=prices.length;
        int[][] f=new int[n][3]; //最多完成两次交易， 0  1  2 
        int[][] g=new int[n][3];
        //初始化，
        int INF=0x3f3f3f3f; //无溢出
        for(int j=0;j<3;j++){
            f[0][j]=g[0][j]=-INF;
        }
        f[0][0]=-prices[0];g[0][0]=0;
        //填表
        for(int i=1;i<n;i++){
            for(int j=0;j<3;j++){
                f[i][j]=Math.max(f[i-1][j],g[i-1][j]-prices[i]);
                if(j==0){
                    g[i][j]=g[i-1][j]; //特殊处理
                }else{
                    g[i][j]=Math.max(g[i-1][j],f[i-1][j-1]+prices[i]);
                }
            }
        }
        return Math.max(g[n-1][0], Math.max(g[n-1][1], g[n-1][2]));
    }
}

第六题：最多k次交易

本题和上一题分析思路完全一致，只是限制条件变为k，直接来看代码改动即可

class Solution {
    //本道题限制次数k次
    public int maxProfit(int k, int[] prices) {
        //建表
        int n=prices.length;
        int[][] f=new int[n][k+1]; //0~k次交易
        int[][] g=new int[n][k+1];
        //初始化
        int INF=0x3f3f3f3f; //无溢出
        for(int j=0;j<k;j++){
            f[0][j]=g[0][j]=-INF;
        }
        f[0][0]=-prices[0];g[0][0]=0;
        //填表
        for(int i=1;i<n;i++){
            for(int j=0;j<k+1;j++){
                f[i][j]=Math.max(f[i-1][j],g[i-1][j]-prices[i]);
                if(j==0){
                    g[i][j]=g[i-1][j]; //特殊处理
                }else{
                    g[i][j]=Math.max(g[i-1][j],f[i-1][j-1]+prices[i]);
                }
            }
        }
        int ret=0;
        //最大值在g[n-1][j]里面选最大值即可
        for(int j=0;j<k+1;j++){
           ret=Math.max(ret,g[n-1][j]);
        }
        return ret;
        
    }
}