特征降维
特征降维目的?
-
降维增加数据密度
-
提升模型性能
-
降低计算成本
-
改善数据可视化
-
去除噪声和冗余
• 特征降维涉及的知识面比较多,当前阶段常用的方法:
(1)低方差过滤法
(2)PCA(主成分分析)降维法
(3)相关系数(皮尔逊相关系数、斯皮尔曼相关系数)
低方差过滤法
低方差过滤法:指的是删除方差低于某些阈值的一些特征
• 特征方差小:特征值的波动范围小,包含的信息少,模型很难学习到信息
• 特征方差大:特征值的波动范围大,包含的信息相对丰富,便于模型进行学习
方差公式
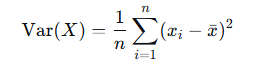
代码
python
# 1.导入依赖包
from sklearn.feature_selection import VarianceThreshold
import pandas as pd
import numpy as np
# 2. 读取数据集
# 原始数据矩阵:5行(样本) × 4列(特征)
X = np.array([
[3, 5, 1, 100], # 样本1
[3, 6, 1, 105], # 样本2
[3, 4, 1, 95], # 样本3
[3, 5, 1, 102], # 样本4
[3, 5, 1, 98] # 样本5
])
# 3. 使用方差过滤法, 删除的是方差 ≤ 0.3 的特征
transformer = VarianceThreshold(threshold=0.3)
data = transformer.fit_transform(X)
print(data, data.shape) # (971, 1044)执行结果
python
[[ 5 100]
[ 6 105]
[ 4 95]
[ 5 102]
[ 5 98]] (5, 2)主成分分析PCA
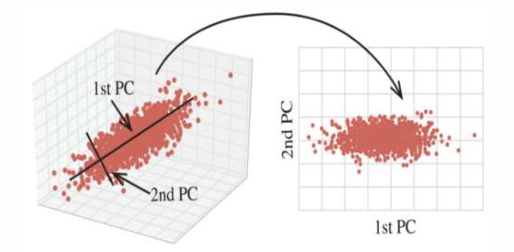
• 主成分分析(Principal Component Analysis,PCA) PCA 通过对数据维数进行压缩,尽可能降低原数据的维数(复杂度) 损失少量信息,在此过程中可能会舍弃原有数据、创造新的变量。
PCA作用 = 特征降维 + 去相关 + 特征提取
去相关
-
多重共线性问题
-
模型参数估计不稳定
-
过拟合风险增加
特征提取
不是简单地选择现有特征,而是创建新特征 ,这些新特征是原始特征的最优线性组合,使特征更明显。
代码
python
# 1.导入依赖包
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
# 2. 加载数据集
x, y = load_iris(return_X_y=True)
print(x[:5], x.shape)
# 3. PCA,保留指定比例的信息,保留95%的原始方差
transformer = PCA(n_components=0.95)
x_pca = transformer.fit_transform(x)
print(x_pca[:5], x_pca.shape)
# 4. PCA,保留指定数量特征,保留2个主成分
transformer = PCA(n_components=2)
x_pca = transformer.fit_transform(x)
print(x_pca[:5], x_pca.shape)
# 4. PCA,保留指定数量特征,保留所有4个主成分
transformer = PCA(n_components=None)
x_pca = transformer.fit_transform(x)
print(x_pca[:5], x_pca.shape)执行结果
python
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]] (150, 4)
[[-2.68412563 0.31939725]
[-2.71414169 -0.17700123]
[-2.88899057 -0.14494943]
[-2.74534286 -0.31829898]
[-2.72871654 0.32675451]] (150, 2)
[[-2.68412563 0.31939725]
[-2.71414169 -0.17700123]
[-2.88899057 -0.14494943]
[-2.74534286 -0.31829898]
[-2.72871654 0.32675451]] (150, 2)
[[-2.68412563e+00 3.19397247e-01 -2.79148276e-02 -2.26243707e-03]
[-2.71414169e+00 -1.77001225e-01 -2.10464272e-01 -9.90265503e-02]
[-2.88899057e+00 -1.44949426e-01 1.79002563e-02 -1.99683897e-02]
[-2.74534286e+00 -3.18298979e-01 3.15593736e-02 7.55758166e-02]
[-2.72871654e+00 3.26754513e-01 9.00792406e-02 6.12585926e-02]] (150, 4)特征降维 -- 相关系数
• 相关系数:反映特征列之间(变量之间)密切相关程度的统计指标
• 常见2个相关系数:皮尔逊相关系数、斯皮尔曼相关系数
• 相关系数的值介于--1与+1之间,即--1 ≤ r ≤ +1。其性质如下:
当 r > 0 时,表示两变量正相关,r < 0 时,两变量为负相关
当 |r| = 1 时,表示两变量为完全相关,当r = 0时,表示两变量间无相关关系
当 0 < |r| < 1时,表示两变量存在一定程度的相关。
且|r|越接近1,两变量间线性关系越密切;|r|越接近于0,表示两变量的线性相关越弱
• 一般可按三级划分:
(1) |r| <0.4为低度相关;
(2) 0.4≤ |r| <0.7为显著性相关;
(3) 0.7 ≤ |r| <1为高度线性相关。
皮尔逊相关系数
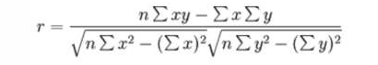
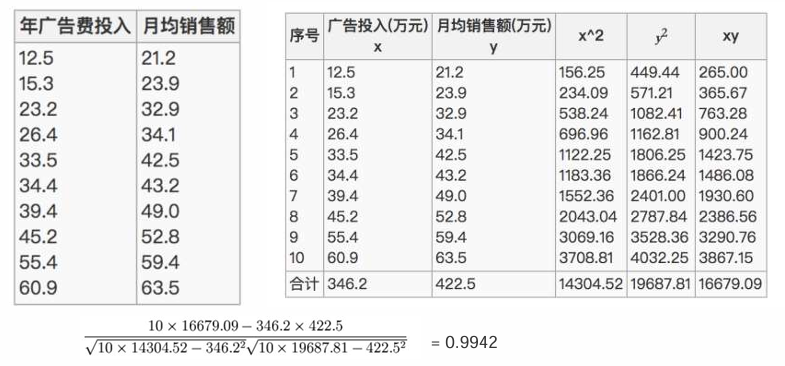
• 举个例子:已知广告投入x特征与月均销售额y之间的关系,经过皮尔逊相关系数计算,为高度相关。
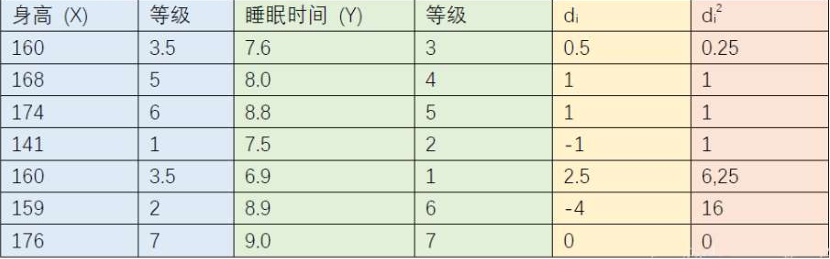
斯皮尔曼相关系数
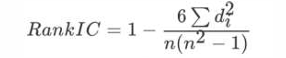
n为等级个数,d为成对变量的等级差数
代码
python
# 1.导入依赖包
import pandas as pd
from sklearn.decomposition import PCA
from sklearn.feature_selection import VarianceThreshold
from scipy.stats import pearsonr
from scipy.stats import spearmanr
from sklearn.datasets import load_iris
# 2.读取数据集(鸢尾花数据集)
data = load_iris()
data = pd.DataFrame(data.data, columns=data.feature_names)
print(data.head(2))
# 3. 皮尔逊相关系数
corr = pearsonr(data['sepal length (cm)'], data['sepal width (cm)'])
print('sepal length (cm) --> ', corr, '皮尔逊相关系数:', corr[0], '不相关性概率:', corr[1])
# (-0.11756978413300204, 0.15189826071144918) 皮尔逊相关系数: -0.11756978413300204 不相关性概率:
# 0.15189826071144918
# 4. 斯皮尔曼相关系数
corr = spearmanr(data['sepal length (cm)'], data['sepal width (cm)'])
print('sepal length (cm) --> ', corr, '斯皮尔曼相关系数:', corr[0], '不相关性概率:', corr[1])
# SpearmanrResult(correlation=-0.166777658283235, pvalue=0.04136799424884587) 斯皮尔曼相关系数: -0.166777658283235 不
# 相关性概率: 0.04136799424884587
transformer = PCA(n_components=0.95)
x_pca = transformer.fit_transform(data)
print(x_pca[:5], x_pca.shape)- 先用自动化方法(VarianceThreshold / SelectKBest / PCA 等)粗筛一遍,把明显没用的、低方差的、与目标弱相关的特征先干掉(变成"垃圾堆")。
- 然后再从"垃圾堆"里挑几个回来,手动/半自动验证它们是不是真的没用(可能被误删了)。
- 如果验证后发现它们其实有用(比如对某些类别有区分力),就加回来。