leetcode链表 - 技术栈

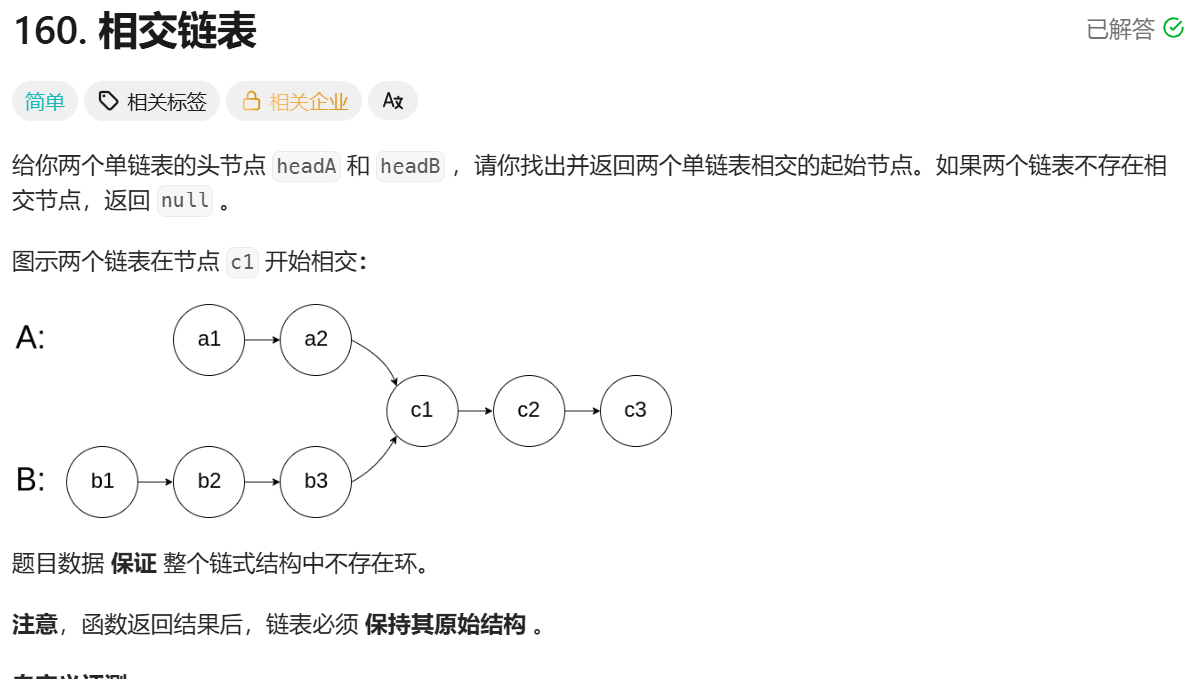
第160题是找出两个链表第一次相交的节点并返回

暴力解法：

就是O（m*n）双层for循环

哈希表法：稍微暴力

把第一条链表遍历，每个节点都存入set；然后遍历第二个链表，每个节点都从set中找一下，如果找到了就返回。最后返回null

时间复杂度O(m+n)，空间复杂度是m或者n（开辟了set）

javascript 复制代码

/**
 * @param {ListNode} headA
 * @param {ListNode} headB
 * @return {ListNode}
 */
var getIntersectionNode = function(headA, headB) {
    // 初始化哈希集合，用于存储链表A的所有节点
    const nodeSet = new Set();
    let cur = headA; // 指针遍历链表A

    // 第一步：遍历链表A，将所有节点加入Set
    while (cur) {
        nodeSet.add(cur); // 存节点对象，不是cur.val！
        cur = cur.next;   // 指针后移
    }

    cur = headB; // 重置指针，遍历链表B
    // 第二步：遍历链表B，检查节点是否在Set中
    while (cur) {
        if (nodeSet.has(cur)) {
            return cur; // 找到第一个相交节点，直接返回
        }
        cur = cur.next;
    }

    // 遍历结束未找到，返回null
    return null;
};

双指针法

定义两个指针pA、pB，分别从headA、headB出发，以相同速度 遍历链表，当某个指针走到链表末尾（null）时，将其重置为另一个链表的头节点 ，继续遍历，最终两个指针会在第一个相交节点处相遇 ；若链表不相交，两个指针会同时走到null。

核心原理（为什么会相遇？）

假设链表 A 长度为m，链表 B 长度为n，相交部分长度为k，则：

链表 A 独有的部分长度：m - k；
链表 B 独有的部分长度：n - k。

两个指针最终走的总步数相同 （相遇时为m + n - k；不相遇为m+n）：

pA的路径：A 独有的部分 → 相交部分 → B 独有的部分；
pB的路径：B 独有的部分 → 相交部分 → A 独有的部分。

假设走到总步数m + n时，无论m和n谁大，两个指针都会在第一个相交节点 相遇（相交时，就是可能在前面就相遇了），或同时走到null（不相交时）

javascript 复制代码

/**
 * @param {ListNode} headA
 * @param {ListNode} headB
 * @return {ListNode}
 */
var getIntersectionNode = function(headA, headB) {
    // 边界处理：若任一链表为空，直接返回null（无相交可能）
    if (!headA || !headB) return null;

    let pA = headA, pB = headB;
    // 循环：直到两个指针相遇
    while (pA !== pB) {
        // pA走到末尾则重置为headB，否则后移
        pA = pA === null ? headB : pA.next;
        // pB走到末尾则重置为headA，否则后移
        pB = pB === null ? headA : pB.next;
    }
    // 相遇时，pA/pB要么是相交节点，要么是null
    return pA;
};

时间复杂度O（m+n），空间复杂度O（1），只开辟了两个指针，底层还得是小学数学