Flutter for OpenHarmony 进阶：推箱子游戏算法与关卡设计深度解析

欢迎加入开源鸿蒙跨平台社区：开源鸿蒙跨平台开发者社区

Flutter for OpenHarmony 进阶：推箱子游戏算法与关卡设计深度解析

文章目录

• [Flutter for OpenHarmony 进阶：推箱子游戏算法与关卡设计深度解析](#Flutter for OpenHarmony 进阶：推箱子游戏算法与关卡设计深度解析)
• • 摘要
  • 一、推箱子算法基础
  • • [1.1 游戏状态表示](#1.1 游戏状态表示)
    • [1.2 状态空间](#1.2 状态空间)
  • 二、移动算法详解
  • • [2.1 基本移动逻辑](#2.1 基本移动逻辑)
    • [2.2 推箱子逻辑](#2.2 推箱子逻辑)
    • [2.3 碰撞检测流程](#2.3 碰撞检测流程)
  • 三、自动求解算法
  • • [3.1 深度优先搜索（DFS）](#3.1 深度优先搜索（DFS）)
    • [3.2 广度优先搜索（BFS）](#3.2 广度优先搜索（BFS）)
    • [3.3 A*算法](#3.3 A*算法)
  • 四、关卡设计原理
  • • [4.1 可解性判断](#4.1 可解性判断)
    • [4.2 关卡生成算法](#4.2 关卡生成算法)
    • [4.3 难度评估](#4.3 难度评估)
  • 五、状态压缩与优化
  • • [5.1 状态哈希](#5.1 状态哈希)
    • [5.2 双向BFS](#5.2 双向BFS)
  • 六、算法复杂度分析
  • • [6.1 时间复杂度](#6.1 时间复杂度)
    • [6.2 空间复杂度](#6.2 空间复杂度)
  • 七、总结

摘要

推箱子游戏不仅是有趣的益智游戏，更是理解算法和数据结构的绝佳案例。本文深入讲解推箱子游戏的核心算法实现、关卡设计原理、状态空间搜索、自动求解等高级技术点。通过本文学习，读者将掌握推箱子游戏的算法设计思路，了解如何使用递归回溯算法实现自动求解功能。

---

一、推箱子算法基础

1.1 游戏状态表示

推箱子游戏的状态可以用以下数据结构表示：

class GameState {
  final List<List<int>> map;     // 地图
  final Point player;            // 玩家位置
  final List<Point> boxes;       // 箱子位置列表

  GameState({
    required this.map,
    required this.player,
    required this.boxes,
  });

  // 复制状态
  GameState copy() {
    return GameState(
      map: map.map((row) => List<int>.from(row)).toList(),
      player: Point(player.x, player.y),
      boxes: boxes.map((p) => Point(p.x, p.y)).toList(),
    );
  }
}

1.2 状态空间

推箱子游戏的状态空间包括：

• 玩家位置：地图上的任意空格
• 箱子位置：所有可能的组合
• 移动动作：上下左右四个方向

状态总数计算：

• 玩家位置：O(W×H)
• 箱子位置：O((W×H)^n)，n为箱子数
• 总状态数：O(W×H×(W×H)^n)

---

二、移动算法详解

2.1 基本移动逻辑

class MoveResult {
  final bool success;
  final GameState? newState;
  final String? message;

  MoveResult({required this.success, this.newState, this.message});
}

MoveResult tryMove(GameState state, int dx, int dy) {
  final newX = state.player.x + dx;
  final newY = state.player.y + dy;

  // 边界检查
  if (!_isValidPosition(newX, newY, state.map)) {
    return MoveResult(success: false, message: '超出边界');
  }

  final targetCell = state.map[newY][newX];

  // 碰到墙
  if (targetCell == 1) {
    return MoveResult(success: false, message: '碰到墙壁');
  }

  // 碰到箱子
  if (targetCell == 2 || targetCell == 5) {
    return _tryPushBox(state, newX, newY, dx, dy);
  }

  // 移动到空地
  final newState = state.copy();
  newState.player = Point(newX, newY);
  return MoveResult(success: true, newState: newState);
}

2.2 推箱子逻辑

MoveResult _tryPushBox(GameState state, int boxX, int boxY, int dx, int dy) {
  final boxNewX = boxX + dx;
  final boxNewY = boxY + dy;

  // 检查箱子新位置
  if (!_isValidPosition(boxNewX, boxNewY, state.map)) {
    return MoveResult(success: false, message: '箱子超出边界');
  }

  final boxTargetCell = state.map[boxNewY][boxNewX];

  // 箱子后面是障碍
  if (boxTargetCell == 1 || boxTargetCell == 2 || boxTargetCell == 5) {
    return MoveResult(success: false, message: '箱子被阻挡');
  }

  // 创建新状态
  final newState = state.copy();

  // 更新箱子位置
  final boxIndex = state.boxes.indexWhere((p) => p.x == boxX && p.y == boxY);
  newState.boxes[boxIndex] = Point(boxNewX, boxNewY);

  // 更新地图
  if (state.map[boxY][boxX] == 5) {
    newState.map[boxY][boxX] = 3;  // 从目标点移开
  } else {
    newState.map[boxY][boxX] = 0;  // 从空地移开
  }

  if (boxTargetCell == 3) {
    newState.map[boxNewY][boxNewX] = 5;  // 推到目标点
  } else {
    newState.map[boxNewY][boxNewX] = 2;  // 推到空地
  }

  // 移动玩家
  newState.player = Point(boxX, boxY);

  return MoveResult(success: true, newState: newState);
}

2.3 碰撞检测流程

---

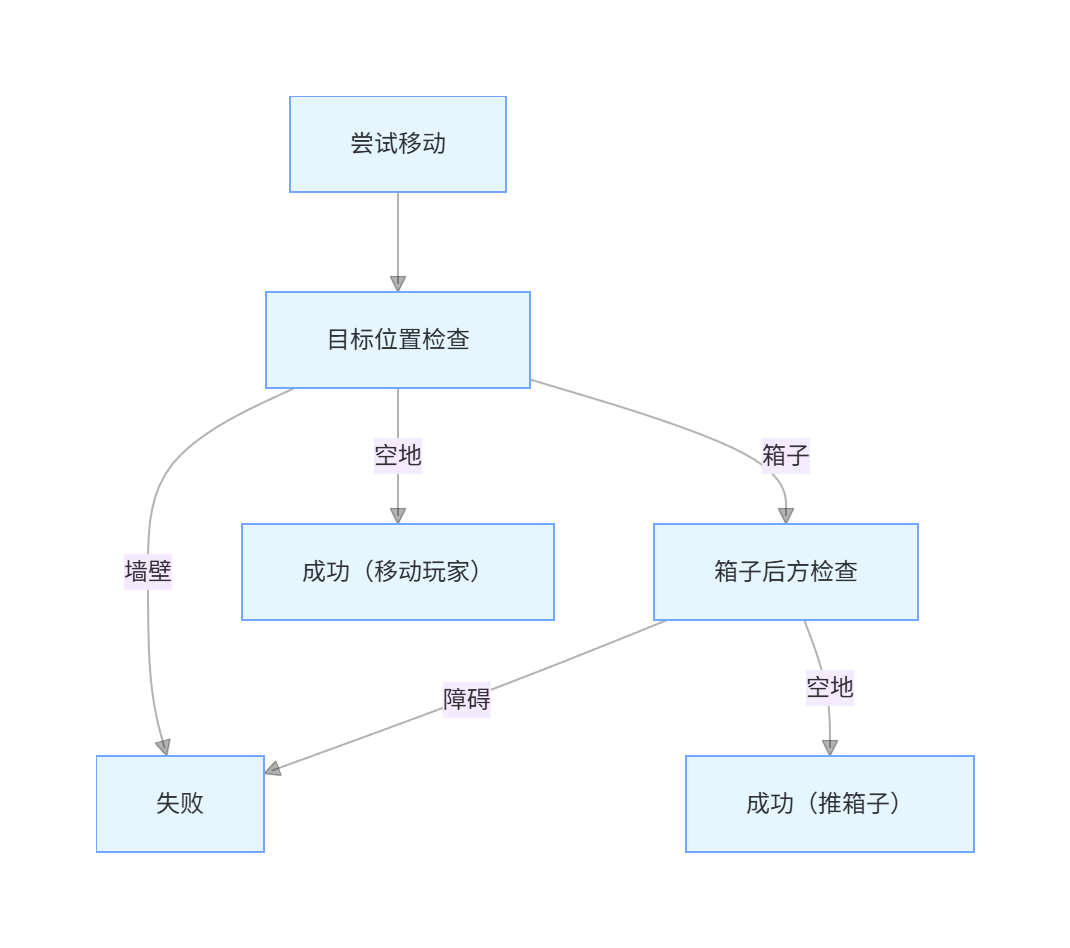
三、自动求解算法

3.1 深度优先搜索（DFS）

class Solution {
  final List<MoveDirection> moves;
  final int steps;

  Solution({required this.moves, required this.steps});
}

Solution? solveDFS(GameState initial, int maxDepth) {
  final visited = <String>{};
  final moves = <MoveDirection>[];

  Solution? _dfs(GameState state, int depth) {
    // 检查胜利
    if (_isWin(state)) {
      return Solution(moves: List.from(moves), steps: moves.length);
    }

    // 达到最大深度
    if (depth >= maxDepth) {
      return null;
    }

    // 记录访问状态
    final stateKey = _getStateKey(state);
    if (visited.contains(stateKey)) {
      return null;
    }
    visited.add(stateKey);

    // 尝试四个方向
    for (final direction in MoveDirection.values) {
      final result = _tryMove(state, direction);
      if (result.success && result.newState != null) {
        moves.add(direction);

        final solution = _dfs(result.newState!, depth + 1);
        if (solution != null) {
          return solution;
        }

        moves.removeLast();
      }
    }

    return null;
  }

  return _dfs(initial, 0);
}

3.2 广度优先搜索（BFS）

Solution? solveBFS(GameState initial) {
  final queue = <_Node>[];
  final visited = <String>{};

  queue.add(_Node(initial, []));
  visited.add(_getStateKey(initial));

  while (queue.isNotEmpty) {
    final current = queue.removeAt(0);

    // 检查胜利
    if (_isWin(current.state)) {
      return Solution(moves: current.moves, steps: current.moves.length);
    }

    // 尝试四个方向
    for (final direction in MoveDirection.values) {
      final result = _tryMove(current.state, direction);
      if (result.success && result.newState != null) {
        final stateKey = _getStateKey(result.newState!);
        if (!visited.contains(stateKey)) {
          visited.add(stateKey);
          queue.add(_Node(
            result.newState!,
            [...current.moves, direction],
          ));
        }
      }
    }
  }

  return null;  // 无解
}

class _Node {
  final GameState state;
  final List<MoveDirection> moves;

  _Node(this.state, this.moves);
}

3.3 A*算法

Solution? solveAStar(GameState initial) {
  final openSet = <_AStarNode>[];
  final closedSet = <String>{};

  final startNode = _AStarNode(
    state: initial,
    gScore: 0,
    fScore: _heuristic(initial),
    moves: [],
  );
  openSet.add(startNode);

  while (openSet.isNotEmpty) {
    // 找到fScore最小的节点
    openSet.sort((a, b) => a.fScore.compareTo(b.fScore));
    final current = openSet.removeAt(0);

    // 检查胜利
    if (_isWin(current.state)) {
      return Solution(moves: current.moves, steps: current.moves.length);
    }

    final stateKey = _getStateKey(current.state);
    if (closedSet.contains(stateKey)) {
      continue;
    }
    closedSet.add(stateKey);

    // 尝试四个方向
    for (final direction in MoveDirection.values) {
      final result = _tryMove(current.state, direction);
      if (result.success && result.newState != null) {
        final newKey = _getStateKey(result.newState!);
        if (closedSet.contains(newKey)) continue;

        final gScore = current.gScore + 1;
        final hScore = _heuristic(result.newState!);
        final fScore = gScore + hScore;

        openSet.add(_AStarNode(
          state: result.newState!,
          gScore: gScore,
          fScore: fScore,
          moves: [...current.moves, direction],
        ));
      }
    }
  }

  return null;
}

class _AStarNode {
  final GameState state;
  final int gScore;  // 从起点到当前的实际代价
  final int fScore;  // gScore + hScore
  final List<MoveDirection> moves;

  _AStarNode({
    required this.state,
    required this.gScore,
    required this.fScore,
    required this.moves,
  });
}

// 启发函数：估算到目标的距离
int _heuristic(GameState state) {
  int totalDistance = 0;
  for (final box in state.boxes) {
    // 找到最近的目标点
    int minDist = double.maxFinite.toInt();
    for (int y = 0; y < state.map.length; y++) {
      for (int x = 0; x < state.map[y].length; x++) {
        if (state.map[y][x] == 3) {
          final dist = (box.x - x).abs() + (box.y - y).abs();
          if (dist < minDist) {
            minDist = dist;
          }
        }
      }
    }
    totalDistance += minDist;
  }
  return totalDistance;
}

---

四、关卡设计原理

4.1 可解性判断

一个关卡是可解的必要条件：

bool isSolvable(GameState state) {
  // 1. 检查是否所有箱子都能到达目标点
  if (!_allBoxesReachable(state)) {
    return false;
  }

  // 2. 检查是否有箱子被卡在角落
  if (_hasStuckBox(state)) {
    return false;
  }

  // 3. 检查玩家是否能到达所有必要位置
  if (!_playerCanReachAll(state)) {
    return false;
  }

  return true;
}

bool _allBoxesReachable(GameState state) {
  for (final box in state.boxes) {
    bool canReachTarget = false;
    for (int y = 0; y < state.map.length; y++) {
      for (int x = 0; x < state.map[y].length; x++) {
        if (state.map[y][x] == 3) {
          if (_canReach(state, box, Point(x, y))) {
            canReachTarget = true;
            break;
          }
        }
      }
      if (canReachTarget) break;
    }
    if (!canReachTarget) return false;
  }
  return true;
}

bool _hasStuckBox(GameState state) {
  for (final box in state.boxes) {
    // 检查是否在目标点上
    if (state.map[box.y][box.x] == 3) continue;

    // 检查是否在角落（两边是墙）
    final leftIsWall = _isWall(state, box.x - 1, box.y);
    final rightIsWall = _isWall(state, box.x + 1, box.y);
    final topIsWall = _isWall(state, box.x, box.y - 1);
    final bottomIsWall = _isWall(state, box.x, box.y + 1);

    if ((leftIsWall && topIsWall) ||
        (leftIsWall && bottomIsWall) ||
        (rightIsWall && topIsWall) ||
        (rightIsWall && bottomIsWall)) {
      return true;
    }
  }
  return false;
}

4.2 关卡生成算法

class LevelGenerator {
  final int width;
  final int height;
  final int boxCount;
  final Random _random = Random();

  LevelGenerator({
    required this.width,
    required this.height,
    required this.boxCount,
  });

  GameState generate() {
    while (true) {
      final level = _generateLevel();
      if (level != null && isSolvable(level)) {
        return level;
      }
    }
  }

  GameState? _generateLevel() {
    // 创建空地图
    final map = List.generate(
      height,
      (y) => List.generate(width, (x) => 0),
    );

    // 添加边界墙
    for (int x = 0; x < width; x++) {
      map[0][x] = 1;
      map[height - 1][x] = 1;
    }
    for (int y = 0; y < height; y++) {
      map[y][0] = 1;
      map[y][width - 1] = 1;
    }

    // 随机放置一些内部墙壁
    final wallCount = (width * height * 0.1).toInt();
    for (int i = 0; i < wallCount; i++) {
      final x = _random.nextInt(width - 2) + 1;
      final y = _random.nextInt(height - 2) + 1;
      map[y][x] = 1;
    }

    // 放置玩家
    final player = _findEmptyPosition(map);
    if (player == null) return null;

    // 放置目标点和箱子
    final targets = <Point>[];
    final boxes = <Point>[];

    for (int i = 0; i < boxCount; i++) {
      final target = _findEmptyPosition(map);
      if (target == null) return null;
      map[target.y][target.x] = 3;
      targets.add(target);

      final box = _findEmptyPosition(map);
      if (box == null) return null;
      map[box.y][box.x] = 2;
      boxes.add(box);
    }

    return GameState(
      map: map,
      player: player,
      boxes: boxes,
    );
  }

  Point? _findEmptyPosition(List<List<int>> map) {
    final empty = <Point>[];
    for (int y = 1; y < height - 1; y++) {
      for (int x = 1; x < width - 1; x++) {
        if (map[y][x] == 0) {
          empty.add(Point(x, y));
        }
      }
    }
    if (empty.isEmpty) return null;
    return empty[_random.nextInt(empty.length)];
  }
}

4.3 难度评估

class DifficultyEvaluator {
  int evaluate(GameState state) {
    int score = 0;

    // 1. 箱子数量
    score += state.boxes.length * 10;

    // 2. 箱子到目标点的总距离
    int totalDistance = 0;
    for (final box in state.boxes) {
      int minDist = double.maxFinite.toInt();
      for (int y = 0; y < state.map.length; y++) {
        for (int x = 0; x < state.map[y].length; x++) {
          if (state.map[y][x] == 3) {
            final dist = (box.x - x).abs() + (box.y - y).abs();
            if (dist < minDist) {
              minDist = dist;
            }
          }
        }
      }
      totalDistance += minDist;
    }
    score += totalDistance * 2;

    // 3. 障碍物密度
    int obstacleCount = 0;
    for (final row in state.map) {
      for (final cell in row) {
        if (cell == 1) obstacleCount++;
      }
    }
    score += (obstacleCount / (state.map.length * state.map[0].length) * 50).toInt();

    return score;
  }

  String getDifficultyLabel(int score) {
    if (score < 30) return '简单';
    if (score < 60) return '中等';
    if (score < 100) return '困难';
    return '专家';
  }
}

---

五、状态压缩与优化

5.1 状态哈希

String _getStateKey(GameState state) {
  // 压缩状态为字符串
  final buffer = StringBuffer();

  // 玩家位置
  buffer.write('${state.player.x},${state.player.y};');

  // 箱子位置（排序后）
  final sortedBoxes = List<Point>.from(state.boxes);
  sortedBoxes.sort((a, b) => a.y != b.y ? a.y.compareTo(b.y) : a.x.compareTo(b.x));

  for (final box in sortedBoxes) {
    buffer.write('${box.x},${box.y};');
  }

  return buffer.toString();
}

5.2 双向BFS

Solution? solveBidirectionalBFS(GameState initial) {
  final forwardQueue = <_Node>[];
  final backwardQueue = <_Node>[];
  final forwardVisited = <String, _Node>{};
  final backwardVisited = <String, _Node>{};

  final startNode = _Node(initial, []);
  forwardQueue.add(startNode);
  forwardVisited[_getStateKey(initial)] = startNode;

  // 从目标状态开始
  final goal = _createGoalState(initial);
  final goalNode = _Node(goal, []);
  backwardQueue.add(goalNode);
  backwardVisited[_getStateKey(goal)] = goalNode;

  while (forwardQueue.isNotEmpty && backwardQueue.isNotEmpty) {
    // 正向搜索一步
    if (_stepBFS(forwardQueue, forwardVisited, backwardVisited) case Solution solution) {
      return solution;
    }

    // 反向搜索一步
    if (_stepBFS(backwardQueue, backwardVisited, forwardVisited) case Solution solution) {
      return _reverseSolution(solution);
    }
  }

  return null;
}

---

六、算法复杂度分析

6.1 时间复杂度

算法	时间复杂度	说明
DFS	O(b^d)	b为分支数(4)，d为最大深度
BFS	O(b^d)	最坏情况遍历整个状态空间
A*	O(b^d)	实际通常优于BFS

6.2 空间复杂度

算法	空间复杂度	说明
DFS	O(d)	递归栈深度
BFS	O(b^d)	需要存储所有状态
A*	O(b^d)	需要存储openSet和closedSet

---

七、总结

本文深入讲解了推箱子游戏的算法实现，主要内容包括：

1. 游戏状态：状态表示、状态空间
2. 移动算法：碰撞检测、推箱子逻辑
3. 自动求解：DFS、BFS、A*算法
4. 关卡设计：可解性判断、随机生成
5. 难度评估：多因素综合评分
6. 优化技术：状态压缩、双向搜索

掌握这些算法可以让你设计出更有挑战性和趣味性的推箱子关卡。

---

欢迎加入开源鸿蒙跨平台社区 : 开源鸿蒙跨平台开发者社区