【C++】哈希表

哈希（散列）方法：通过某种函数hashFunc使元素的储存位置与它的关键码之间能够建立一一映射的关系，从而快速查找元素。这种方法构造出来的转换函数称为哈希函数，散列函数，构造出来的结构称为哈希表

一.哈希函数

引入：

1. 我们知道数组的优势在于快速查找某个元素，拿到数组的下标（索引）就直接可以定位到元素的位置
2. 如果想知道一组元素出现的个数，可以创建一个范围足够大的数组，数组内每一个元素值代表相应元素出现的次数，如果插入元素i，就执行A[i]++，删除元素执行A[i]--，搜索元素时检查A[i]是否为0，这种做法用空间换时间
3. 缺点：浪费空间，当遇到字符串时的编码问题
4. 于是需要一种映射函数将大数映射成小数（散列函数），例如：hash[key] = key % size
5. 问题：不同的元素被映射到相同的位置，产生哈希冲突
6. 解决：线性探测，二次探测，开链...

常见哈希函数

• 直接定址法：hash[key] = A*key + B，需要事先知道关键字的分布
• 除留余数法：hash[key] = key % p，将关键码转换成哈希地址
• 平方取中法：对key平方取中间三位，例如：1234平方，取1522756中间3位，227
• 数学分析法：取一组数重复次数最少，得到几位数字，将其反转，右环位移，左环位移。例如电话号码取后四位，得到2345，反转后5432，右换位移5234

二.哈希冲突的解决

闭散列：

闭散列（开放定址法），当出现哈希冲突时，如果哈希表未填满，可以把key存放到冲突位置的下一个空位置

---

寻找方法

• 线性探测：从冲突位置开始，依次向后探测，直到寻到下一个空位置
  • 删除：采用闭散列处理哈希冲突，不能随便删除哈希表已有元素，若直接删除元素会影响其他元素的搜索（索引改变），所以线性探测采用标记的伪删除来删除元素
  • 一旦发生哈希冲突，所有冲突连在一起，容易产生产生数据堆积
  • 标记：EXIST，EMPTY，DELETE
• 二次探测：H = H+ i^2
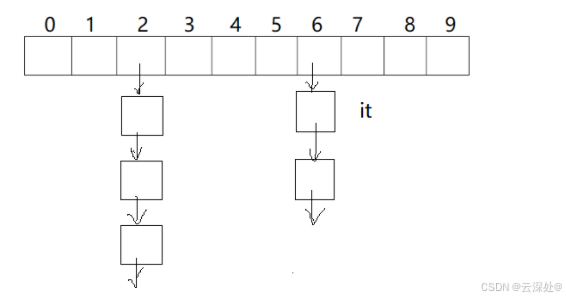
• 开散列：利用哈希桶（数组里面存的链表的地址）

三.哈希表的实现

线性探测：

enum STATE
{
	EXIST,
	EMPTY,
	DELETE
};

template<class K, class V>
struct HashData
{
	pair<K, V> _kv;
	STATE _state = EMPTY;
};

template<class K>
struct DefaultFunc	
{
	size_t operator()(const K& key)
	{
		return (size_t)key;		//转成无符号整型
	}
};

template<>    //类模板的全特化
struct DefaultFunc<string>
{
	size_t operator()(const string& str)
	{
		size_t hash = 0;
		for (auto ch : str)
		{
			hash *= 131;
			hash += ch;
		}
		return hash;
	}
};

template<class K, class V, class HashFunc = DefaultFunc<K>>
class HashTable
{
public:
	//构造函数
	HashTable()
	{
		_table.resize(10);
	}

	bool Insert(const pair<K, V>& kv)
	{
		static HashFunc hf;
		//最低扩容标准
		if (_n * 10 / _table.size() >= 7)
		{
			size_t nsize = _table.size() * 2;
			//遍历旧表，重新映射新表
			HashTable<K, V> newtable;
			newtable._table.resize(nsize);

			for (size_t i = 0; i < _table.size(); i++)
			{
				if (_table[i]._state == EXIST)
				{
					newtable.Insert(_table[i]._kv);
				}
			}
			_table.swap(newtable._table);
		}

		//线性探测
		size_t hashi = hf(kv.first) % _table.size();
		while (_table[hashi]._state == EXIST)
		{
			hashi++;
			hashi %= _table.size();
		}

		_table[hashi]._kv = kv;
		_table[hashi]._state = EXIST;
		_n++;
		return true;
	}

	HashData<const K, V>* Find(const K& key)
	{
		size_t hashi = key % _table.size();
		while (_table[hashi]._state != EMPTY)
		{
			if (_table[hashi]._state == EXIST && _table[hashi]._kv.first == key)
			{
				return (HashData<const K, V>) & _table[hashi];
			}
			hashi++;
			return nullptr;
		}
	}

	bool Erase(const K& key)
	{
		HashData<const K, V>* ret = Find(key);
		if (ret)
		{
			ret->_state = DELETE;
			_n--;
			return true;
		}
		return false;
	}
	void Print()
	{
		for (int i = 0; i < _table.size(); i++)
		{
			if (_table[i]._state == EXIST)
			{
				cout << "键" << ":" << _table[i]._kv.first << "值：" << _table[i]._kv.second << endl;
			}
		}
		cout << endl;
	}

private:
	vector<HashData<K, V>> _table;    //编译器对内置类型不做处理，自定义类型调用析构
	size_t _n = 0;
	
};

开散列：

namespace hash_bucket
{
	template<class K>
	struct DefaultFunc
	{
		size_t operator()(const K& key)
		{
			return key;
		}
	};

	template<>
	struct DefaultFunc<string>
	{
		size_t operator()(const string& kv)
		{
			size_t hash = 0;
			for (auto ch : kv)
			{
				hash *= 131;	//哈希算法，处理字符串
				hash += ch;
			}
			return hash;
		}
	};

	template<class K, class V>
	struct HashNode
	{
		pair<K, V> _kv;
		HashNode<K, V>* _next;

		HashNode(const pair<K, V>& kv) :_kv(kv), _next(nullptr) {}
	};

	template<class K, class V, class HashFunc = DefaultFunc<K>>
	class HashTable
	{
		typedef HashNode<K, V> Node;
	public:
		HashTable()
		{
			_table.resize(10, nullptr);

		}
		~HashTable()
		{
			for (size_t i = 0; i < _table.size(); i++)
			{
				Node* cur = _table[i];
				while (cur)
				{
					Node* next = cur->_next;
					delete cur;
					cur = next;
				}
				_table[i] = nullptr;
			}
		}
		bool Insert(const pair<K,V>& kv)
		{
			static HashFunc hf;
			if (_n == _table.size())
			{
				size_t newSize = _table.size() * 2;
				vector<Node*> newTable(newSize, nullptr);
				//遍历新链表
				for (size_t i = 0; i < _table.size(); i++)
				{
					Node* cur = _table[i];
					while (cur)
					{
						Node* next = cur->_next;

						size_t hashi = hf(cur->_kv.first) % newSize;
						cur->_next = newTable[hashi];
						newTable[hashi] = cur;

						cur = next;
					}
					_table[i] = nullptr;
				}
				_table.swap(newTable);
			}

			size_t hashi = hf(kv.first) % _table.size();
			Node* newnode = new Node(kv);
			newnode->_next = _table[hashi];		//头插
			_table[hashi] = newnode;
			_n++;
			return true;
		}

		Node* Find(const K& key)
		{
			size_t hashi = key % _table.size();
			Node* cur = _table[hashi];
			
			while (cur)
			{
				if (cur->_kv.first == key)
				{
					return cur;
				}
				cur = cur->_next;
			}
			return nullptr;
		}

		bool Erase(const K& key)
		{
			size_t hashi = hf(key) % _table.size();

			Node* prev = nullptr;
			Node* cur = _table[hashi];

			while (cur)
			{
				if (cur->_kv.first == key)
				{
					if (prev == nullptr)
					{
						_table[hashi] = cur->_next;
					}
					else
					{
						prev->_next = cur->_next;
					}
					delete cur;
					_n--;
					return true;
				}
				else
				{
					prev = cur;
					cur = cur->_next;
				}
			}
			return false;
		}

		void Print()
		{
			for (size_t i = 0; i < _table.size(); i++)
			{
				printf("[%d]->", i);
				Node* cur = _table[i];
				while (cur)
				{
					cout << cur->_kv.first << ":" << cur->_kv.second << "->";
					cur = cur->_next;
				}
				printf("NULL\n");
			}
			cout << endl;
		}
	private:
		vector<Node*> _table;    //指针数组，vector被delete后，Node*指向的空间还未删除，需要析构
		size_t _n = 0;
	};
}