
(以下内容全部出自上述课程)
目录
- 串
-
- [1. 定义](#1. 定义)
- [2. 基本操作](#2. 基本操作)
- [3. 小结](#3. 小结)
- 串的存储结构
-
- [1. 顺序存储](#1. 顺序存储)
- [2. 链式存储](#2. 链式存储)
- [3. 基于顺序存储实现基本操作](#3. 基于顺序存储实现基本操作)
- [4. 小结](#4. 小结)
- 朴素模式匹配算法
-
- [1. 什么是字符串的模式匹配](#1. 什么是字符串的模式匹配)
- [2. 朴素模式匹配算法](#2. 朴素模式匹配算法)
- [3. 演示](#3. 演示)
- [4. 小结](#4. 小结)
- KMP算法
-
- [1. 简述](#1. 简述)
- [2. 朴素优化思路](#2. 朴素优化思路)
- [3. 其他位置](#3. 其他位置)
- [4. 结论](#4. 结论)
- [5. 例子](#5. 例子)
- [6. 代码实现](#6. 代码实现)
- 求next数组
-
- [1. 练习1](#1. 练习1)
- [2. 练习2](#2. 练习2)
- [3. 练习3](#3. 练习3)
- [4. 小结](#4. 小结)
- KMP的优化
串
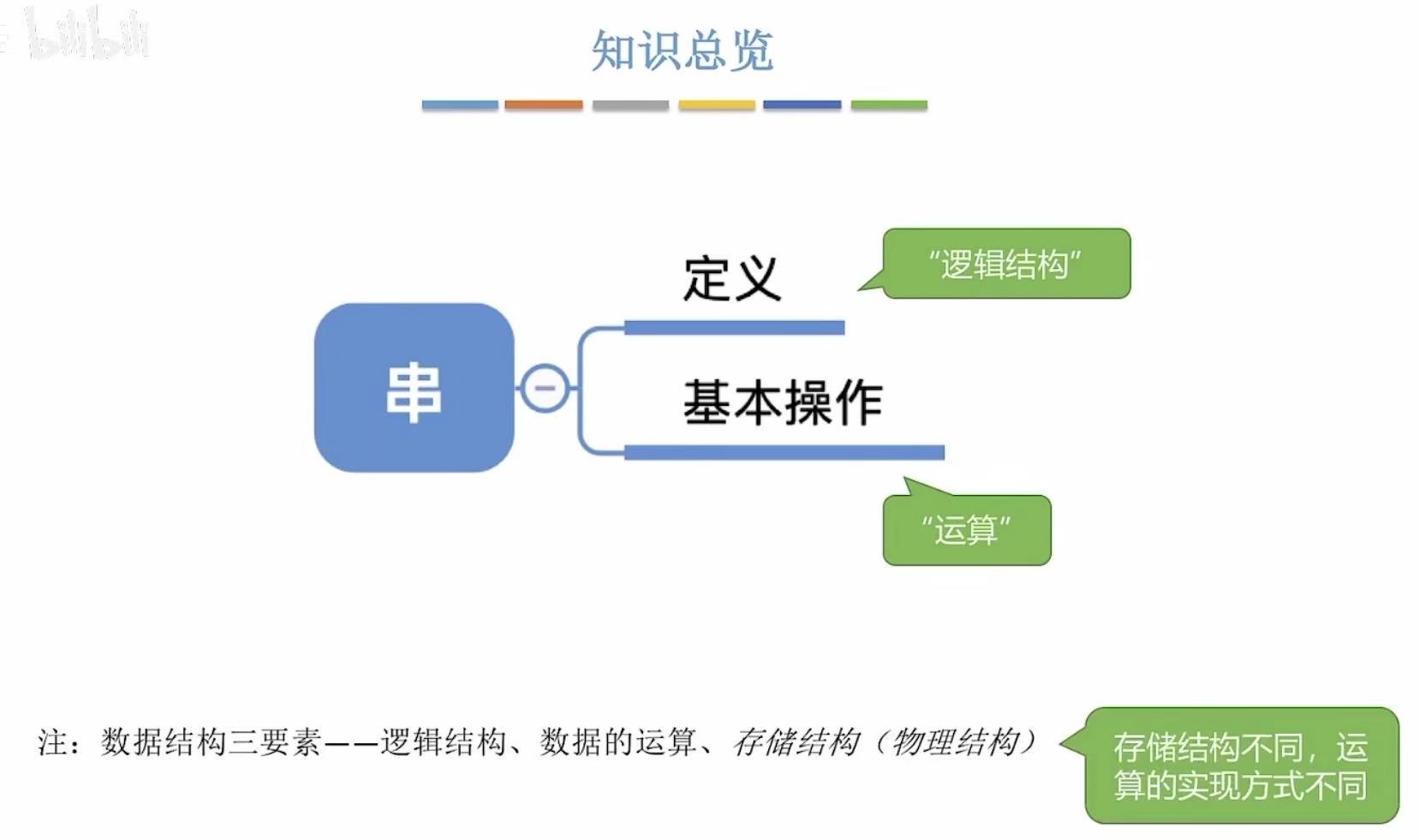
1. 定义
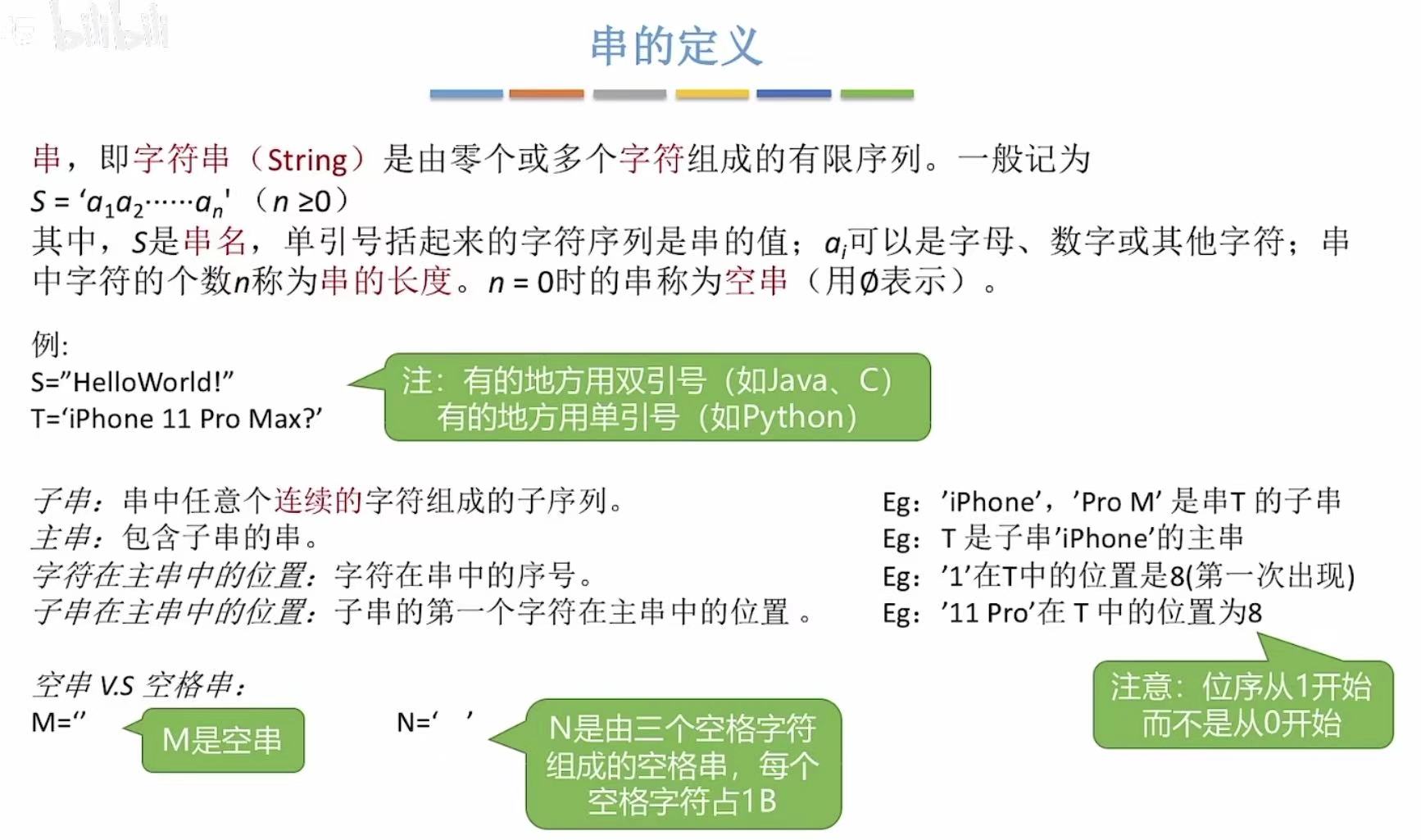
- 串:就是字符串。
- 可以用单引号也可以用双引号。
- 串中的空格也占长度。
- 主串包含子串。
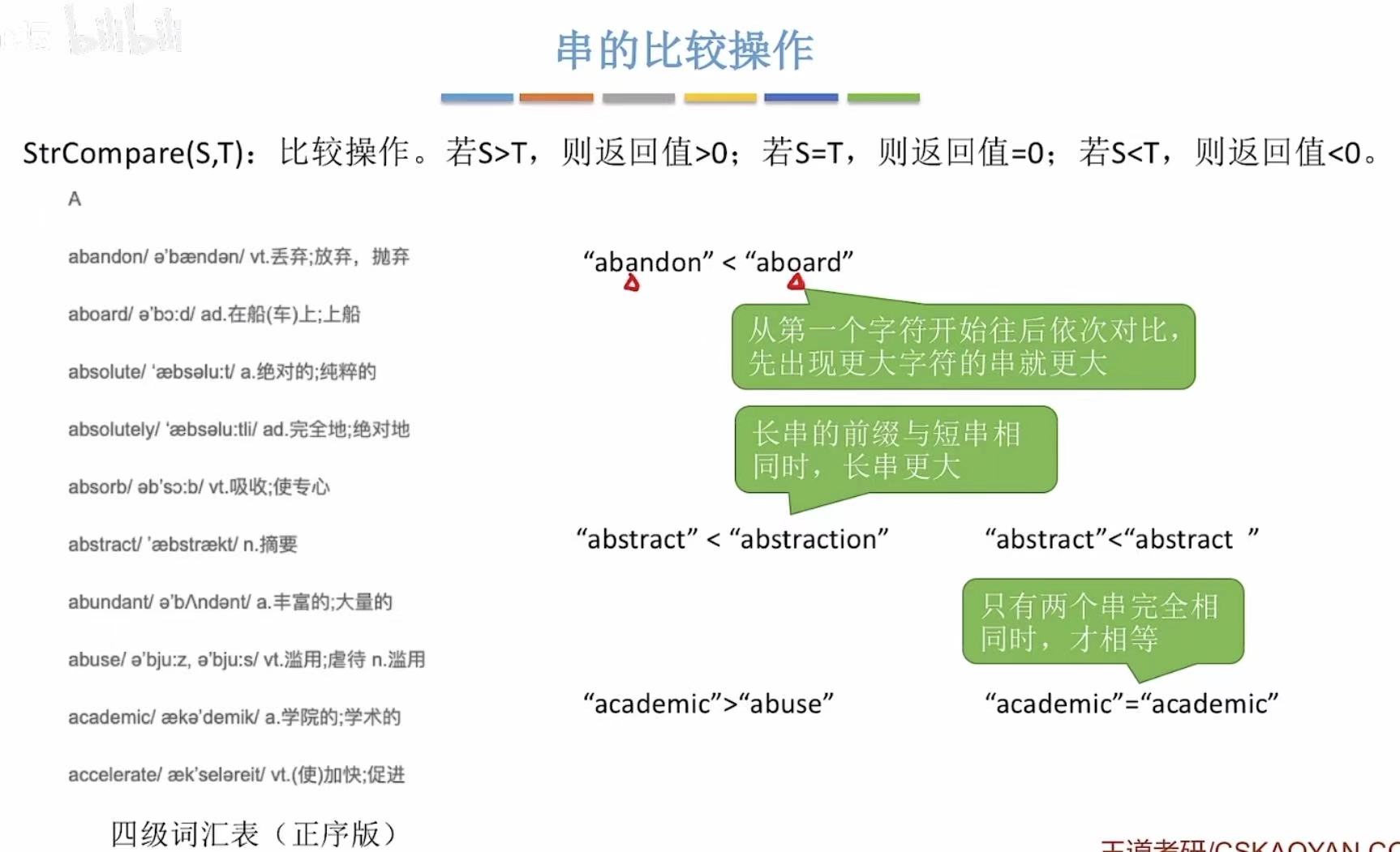
2. 基本操作

类比英文词典的排序:
- 前面先出现的字母比后出现的字母小
- 长度短的在长度长的前面

3. 小结
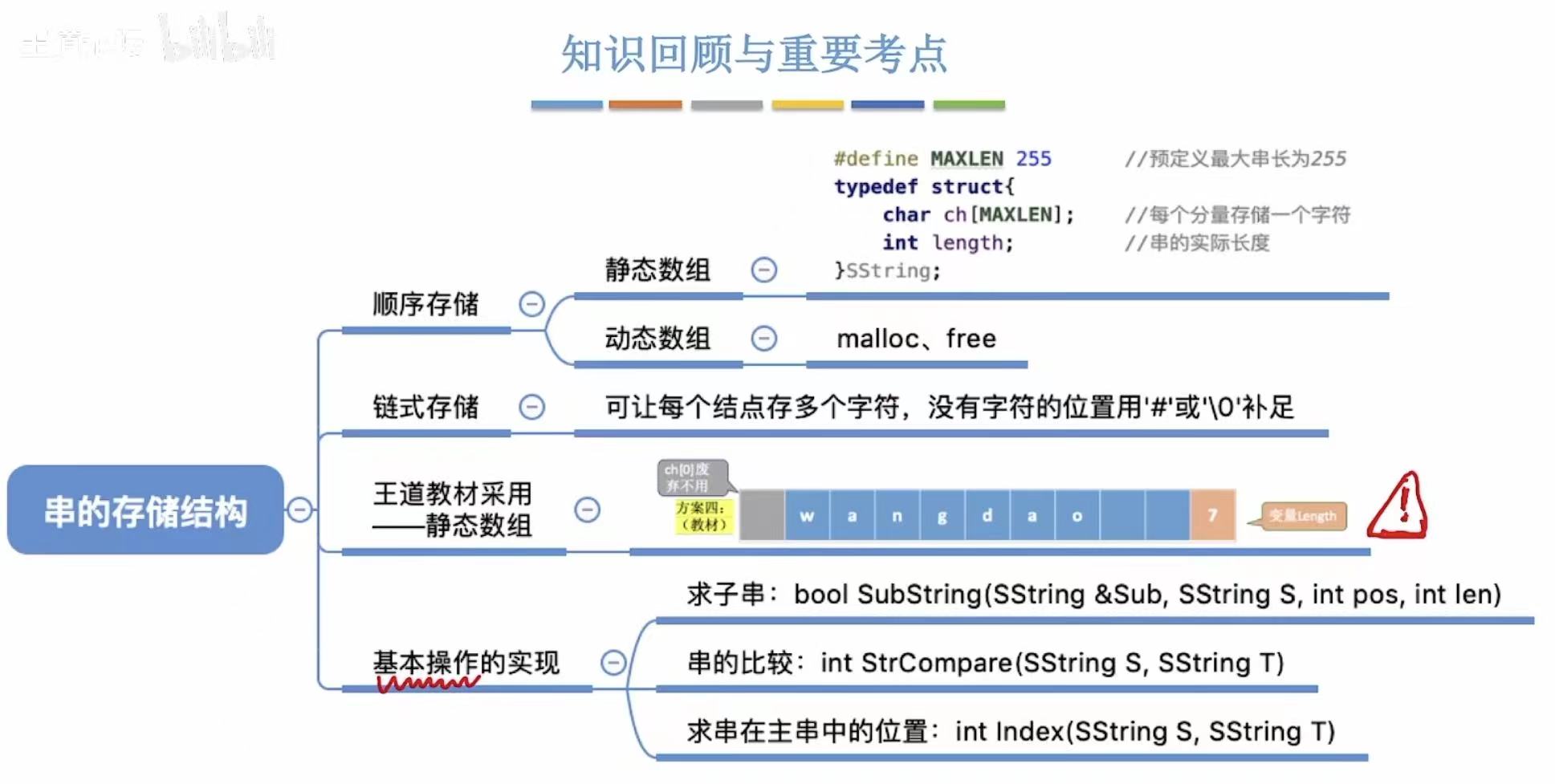
串的存储结构
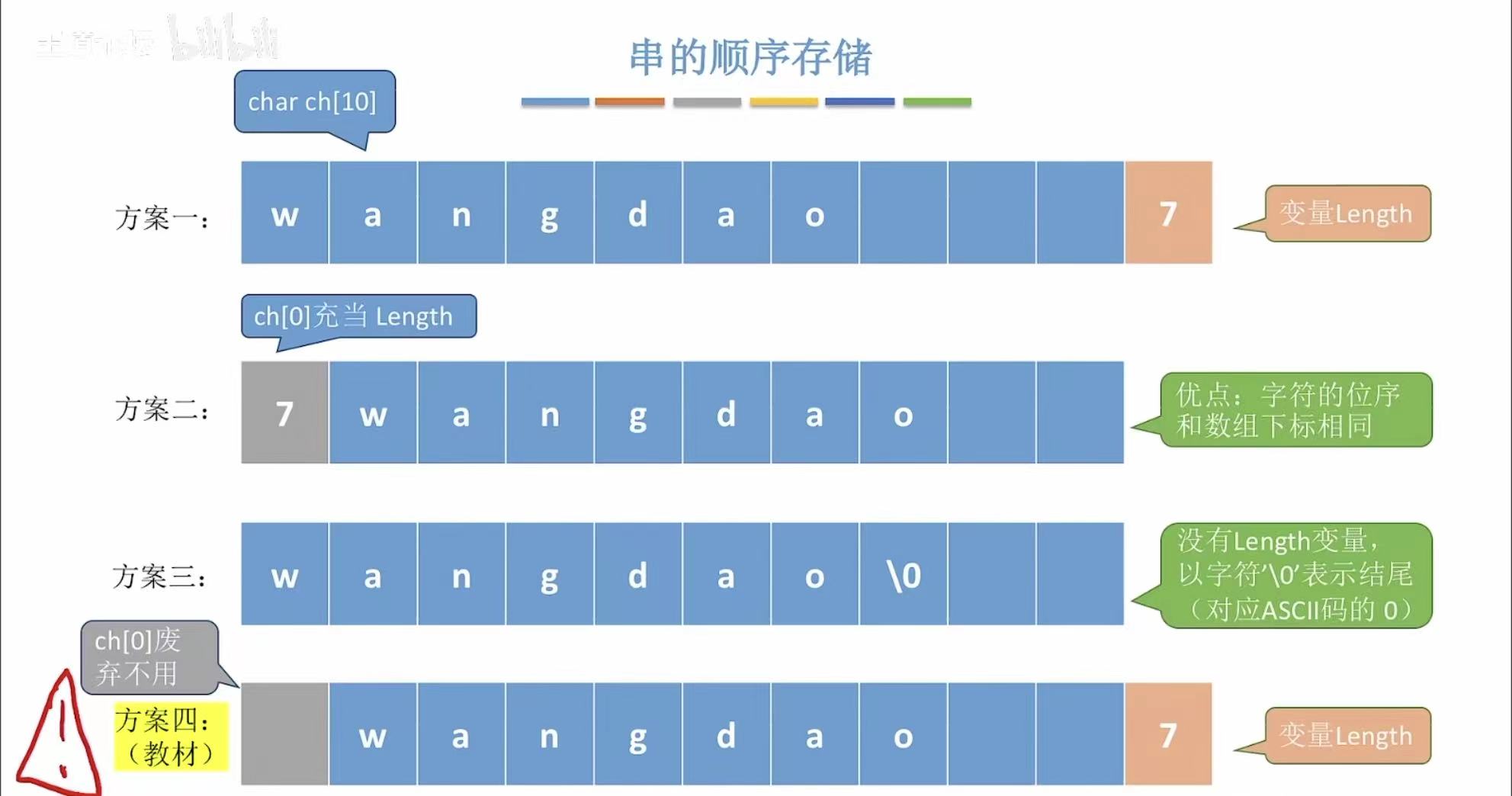
1. 顺序存储
顺序表具体见:顺序表
静态数组实现:
java
#define MAXLEN 255 // 定义宏 MAXLEN 为 255,表示最大字符串长度限制为 255 个字符(即最多 255 字符)。
typedef struct { // 定义一个结构体类型 SString,用于表示字符串。typedef 是为了简化后续使用。
char ch[MAXLEN]; // 存储字符串内容,每个元素放一个字符。例如:ch[0] 是第一个字符。
int length; // 记录当前字符串的实际长度(有效字符数),不是数组大小。
} SString;动态数组实现:
java
typedef struct { // 定义一个新的结构体类型 HString,用于动态存储字符串。
char *ch; // 指向在堆上动态分配的内存块的首地址,用来存放字符串内容。
int length; // 记录当前字符串的实际长度。
} HString;
HString S; // 声明一个 HString 类型的变量 S。
S.ch = (char *)malloc(MAXLEN * sizeof(char)); //在堆上动态分配一块大小为 MAXLEN 的内存空间(共 255 字节),并让 S.ch 指向这块内存的起始地址。
S.length = 0; // 初始化字符串长度为 0,表示当前为空串。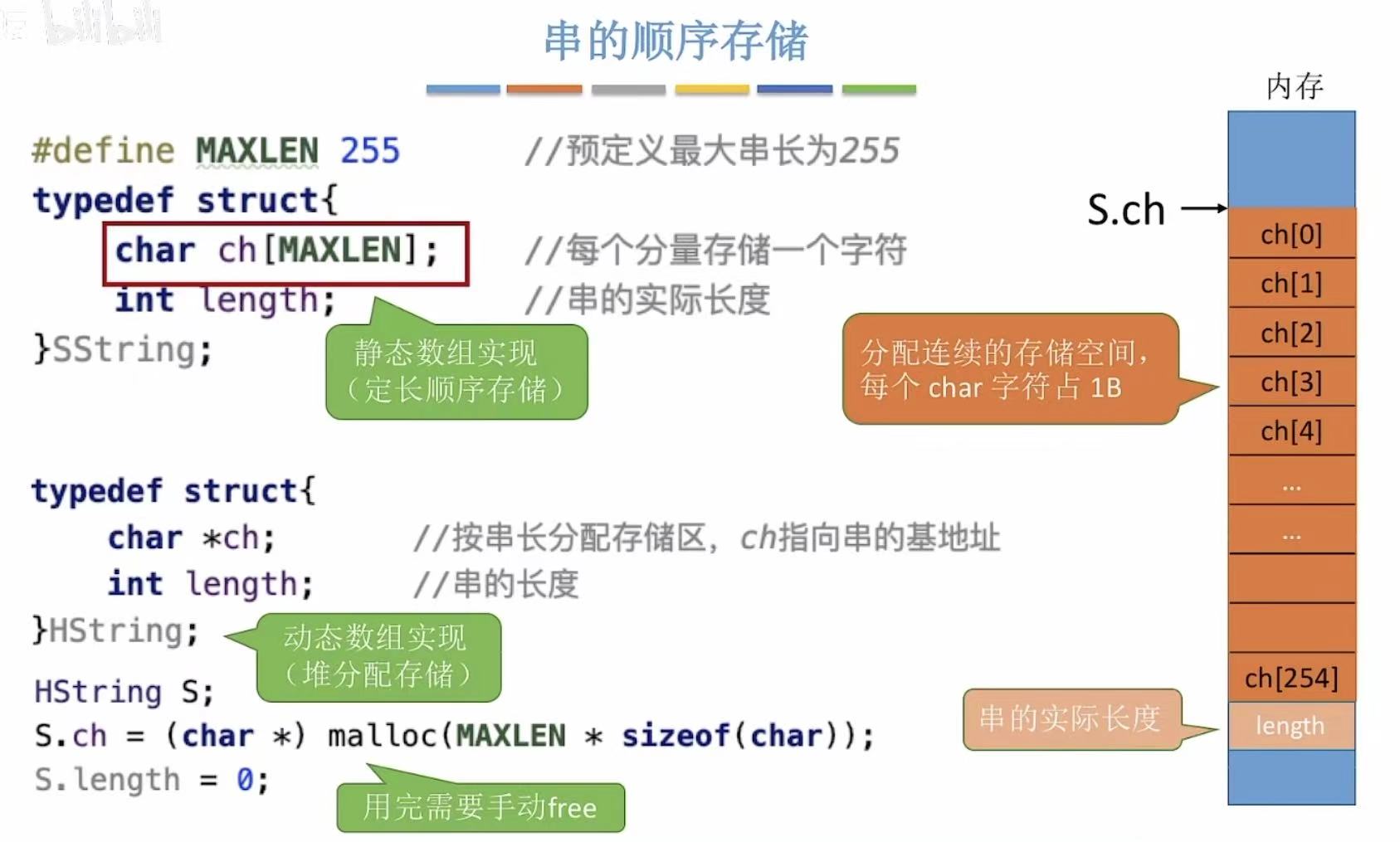
2. 链式存储
链表:链表
单个字符存储:
java
typedef struct StringNode{ // 定义一个结构体类型 StringNode,并同时定义了它的指针类型 String(即 String 是 StringNode* 的别名)。
char ch; // 存储一个字符(如 'a'、'b' 等)。
struct StringNode * next; // 指向下一个节点的地址。如果这是最后一个节点,则 next = NULL。
}StringNode, * String;多个字符存储:
java
typedef struct StringNode{
char ch[4]; // 每个节点包含一个长度为 4 的字符数组,可以存放最多 4 个字符。
struct StringNode * next; // 指向下一个节点的指针。
}StringNode, * String;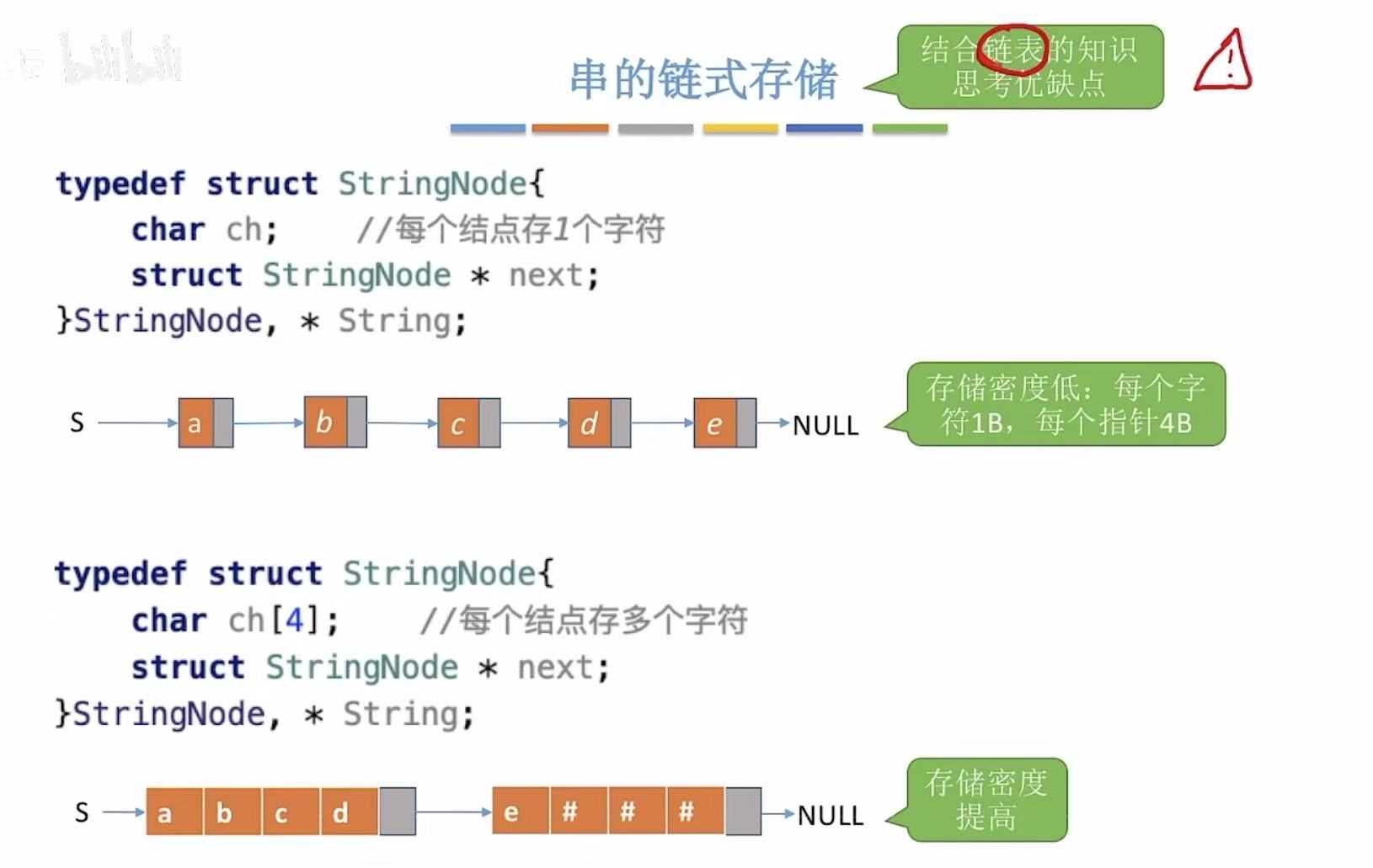
3. 基于顺序存储实现基本操作

java
// 定义一个函数 SubString,用于从源串 S 中提取子串;
// 返回 bool 类型:true 表示成功,false 表示参数非法或越界;
// Sub 是输出参数,使用引用传递(&),用于保存提取出的子串;
// S 是输入的源字符串(按值传递);
// pos 是子串在源串中的起始位置(从 1 开始计数);
// len 是要提取的子串长度。
bool SubString(SString &Sub, SString S, int pos, int len) {
// 检查子串是否越界:
// 起始位置 pos(从1开始)加上长度 len 减1,得到子串最后一个字符的位置;
// 如果该位置大于源串的实际长度 S.length,则说明请求的子串超出了字符串范围,返回 false。
if (pos + len - 1 > S.length)
return false;
// 循环从 pos 到 pos + len - 1(共 len 个字符),
// 将源串 S 中对应位置的字符逐个复制到 Sub 的字符数组中。
for (int i = pos; i < pos + len; i++) {
Sub.ch[i - pos + 1] = S.ch[i];
}
// 设置结果子串 Sub 的实际长度为 len。
Sub.length = len;
// 成功提取子串,返回 true。
return true;
}
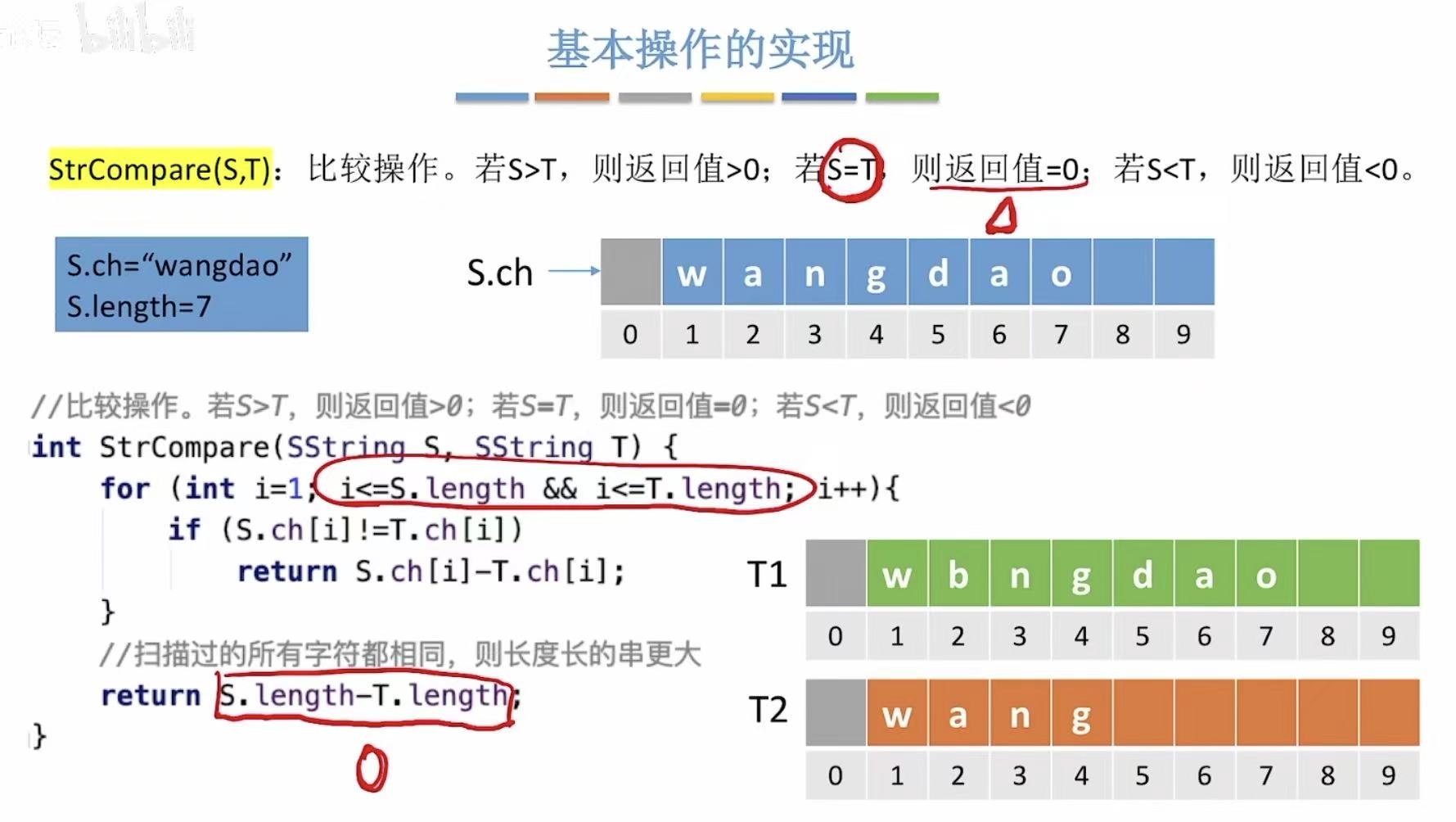
java
// 比较两个字符串 S 和 T 的大小关系。
// 返回值规则:
// 若 S > T,则返回值 > 0;
// 若 S == T,则返回值 = 0;
// 若 S < T,则返回值 < 0。
int StrCompare(SString S, SString T) {
// 从第一个字符(索引1)开始比较,直到其中一个字符串结束或找到不同字符。
// 注意:这里的 i=1 是因为 S.ch[0] 可能不存储有效字符(如教材中"1-based"设计),
// 所以从 ch[1] 开始比较实际内容。
for (int i = 1; i <= S.length && i <= T.length; i++) {
// 如果当前字符不相等,则立即返回它们的 ASCII 差值:
// 若 S.ch[i] > T.ch[i],返回正数 → S > T;
// 若 S.ch[i] < T.ch[i],返回负数 → S < T;
// 此时无需继续比较后续字符。
if (S.ch[i] != T.ch[i]) {
return S.ch[i] - T.ch[i];
}
}
// 如果循环结束,说明前面所有字符都相同。
// 此时比较两个字符串的长度:
// 长度长的字符串更大;
// 因为相同前缀后,更长的串在字典序中更大。
return S.length - T.length;
}
java
// 定位操作:在主串 S 中查找子串 T 第一次出现的位置。
// 若存在,则返回其在 S 中的起始位置(从1开始);
// 若不存在,则返回 0。
int Index(SString S, SString T) {
// i 是当前在主串 S 中尝试匹配的起始位置,从1开始;
// n 是主串 S 的长度;
// m 是子串 T 的长度;
int i = 1, n = StrLength(S), m = StrLength(T);
// 创建一个临时字符串 sub,用于存储从 S 中截取的长度为 m 的子串;
// 该子串将与 T 进行比较。
SString sub;
// 外层循环:枚举主串 S 中所有可能的起始位置;
// 最大只到 n - m + 1,因为如果 i > n - m + 1,
// 则剩下的字符不足以容纳长度为 m 的子串。
while (i <= n - m + 1) {
// 从主串 S 的第 i 个字符开始,提取长度为 m 的子串,存入 sub;
// 即:sub = S[i:i+m-1]
SubString(sub, S, i, m);
// 比较 sub 和 T 是否相等:
// 如果相等(StrCompare 返回 0),说明找到匹配子串;
// 此时不需要返回,继续向后搜索(但通常我们只需要第一次出现);
// 所以这里应该是 **if 相等就 return i**,而不是 ++i。
if (StrCompare(sub, T) == 0)
return i; // ✅ 应该直接返回位置,而不是继续搜索!
// 如果不相等,则移动起始位置 i 向后一位,继续尝试下一个位置。
else
++i;
}
// 如果遍历完所有可能位置都没有找到匹配的子串,则返回 0。
return 0;
}
4. 小结
朴素模式匹配算法
1. 什么是字符串的模式匹配
就是在一大堆文本中,找到你想要的词组。
- 主串:一大串文本,你想找的词语所在的篇章。
- 子串:主串中含有的词语。
- 模式串 :你想找的词语。

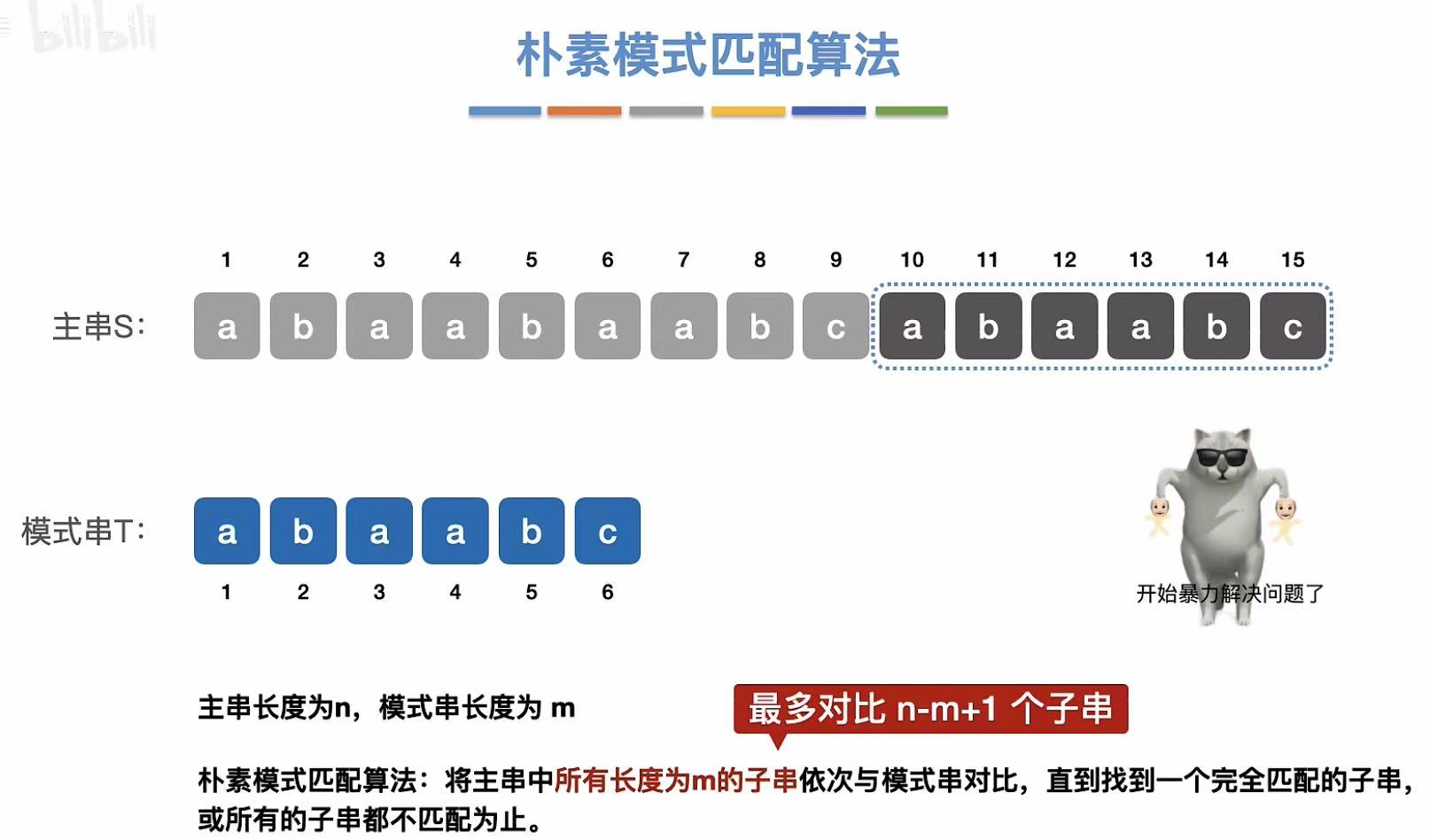
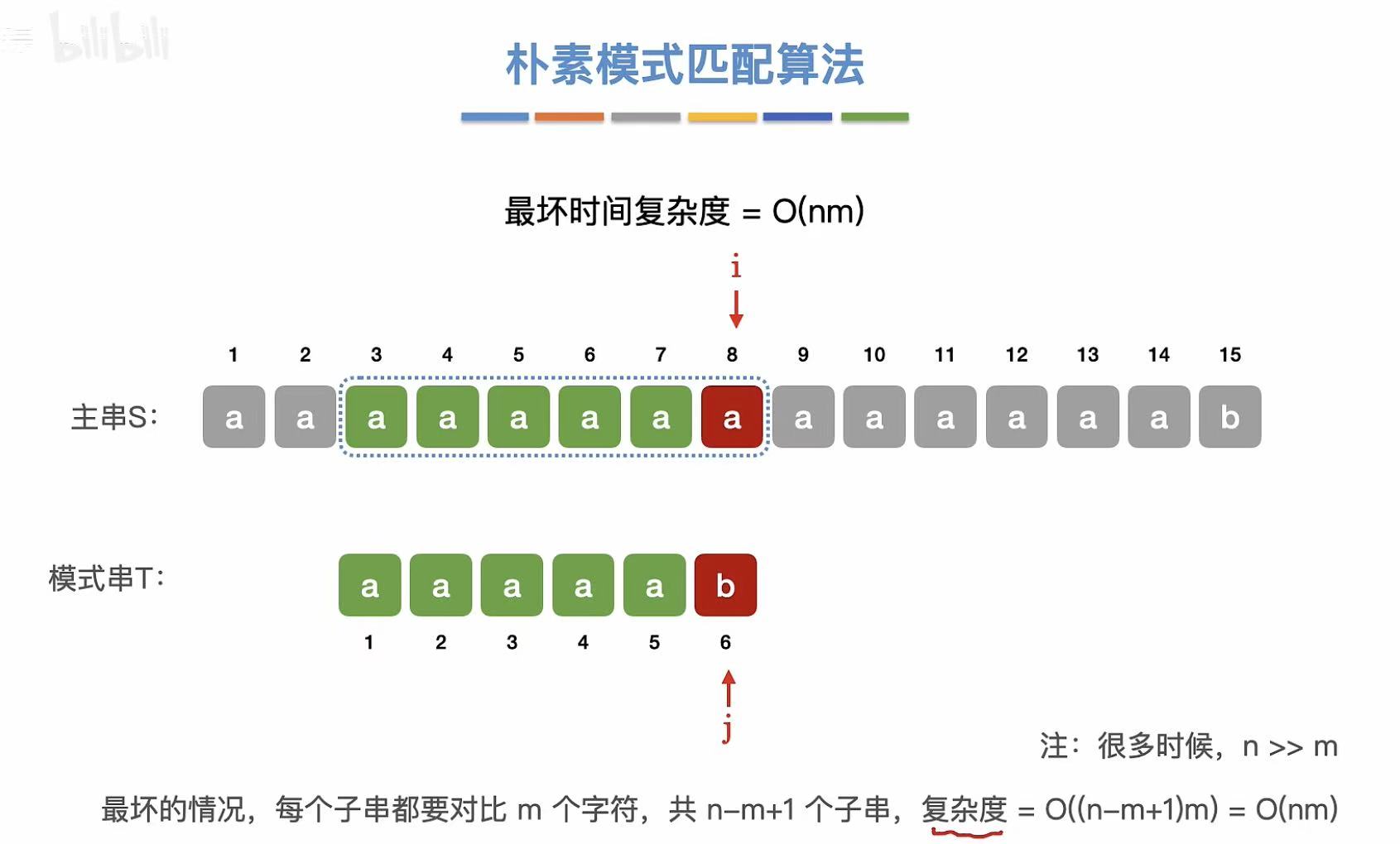
2. 朴素模式匹配算法
朴素:模式串与主串依次比对。
- 123456-->234567-->345678-->456789-->...
- 最终比对到完全符合模式串的子串。
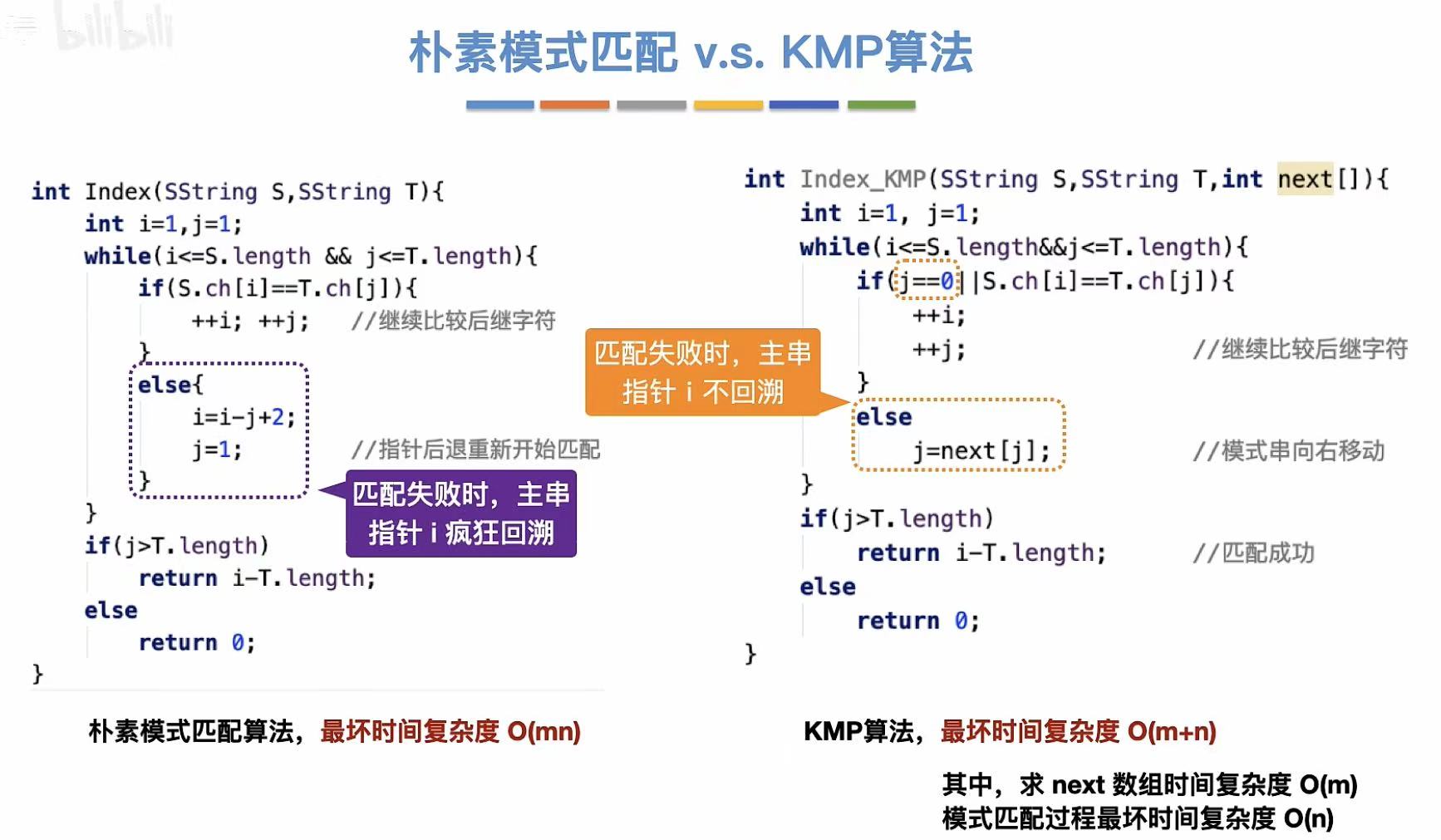
Index(S, T) 函数 :通过调用 SubString 和 StrCompare 实现了朴素模式匹配算法,用于在主串中定位子串首次出现的位置。

3. 演示
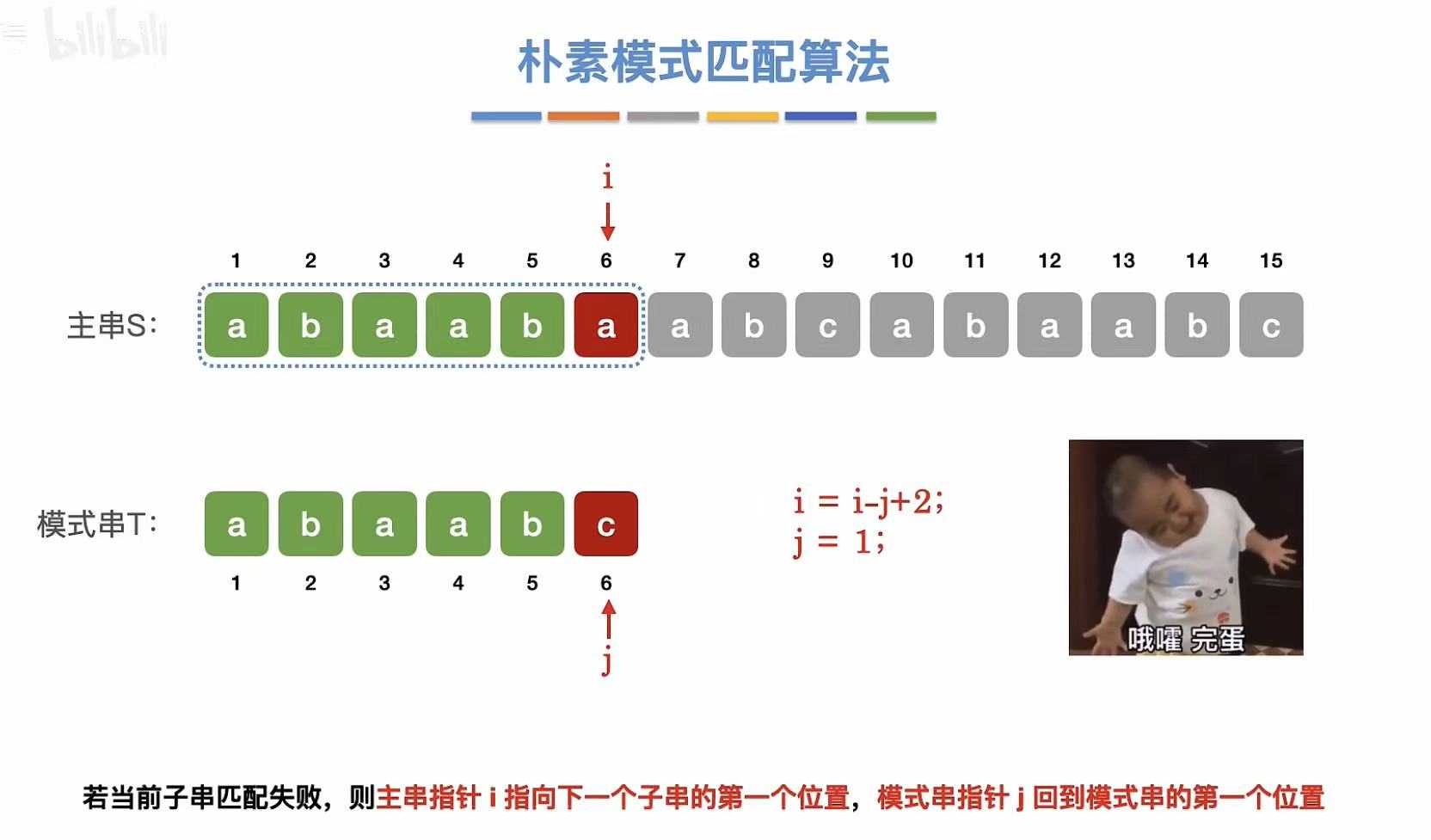
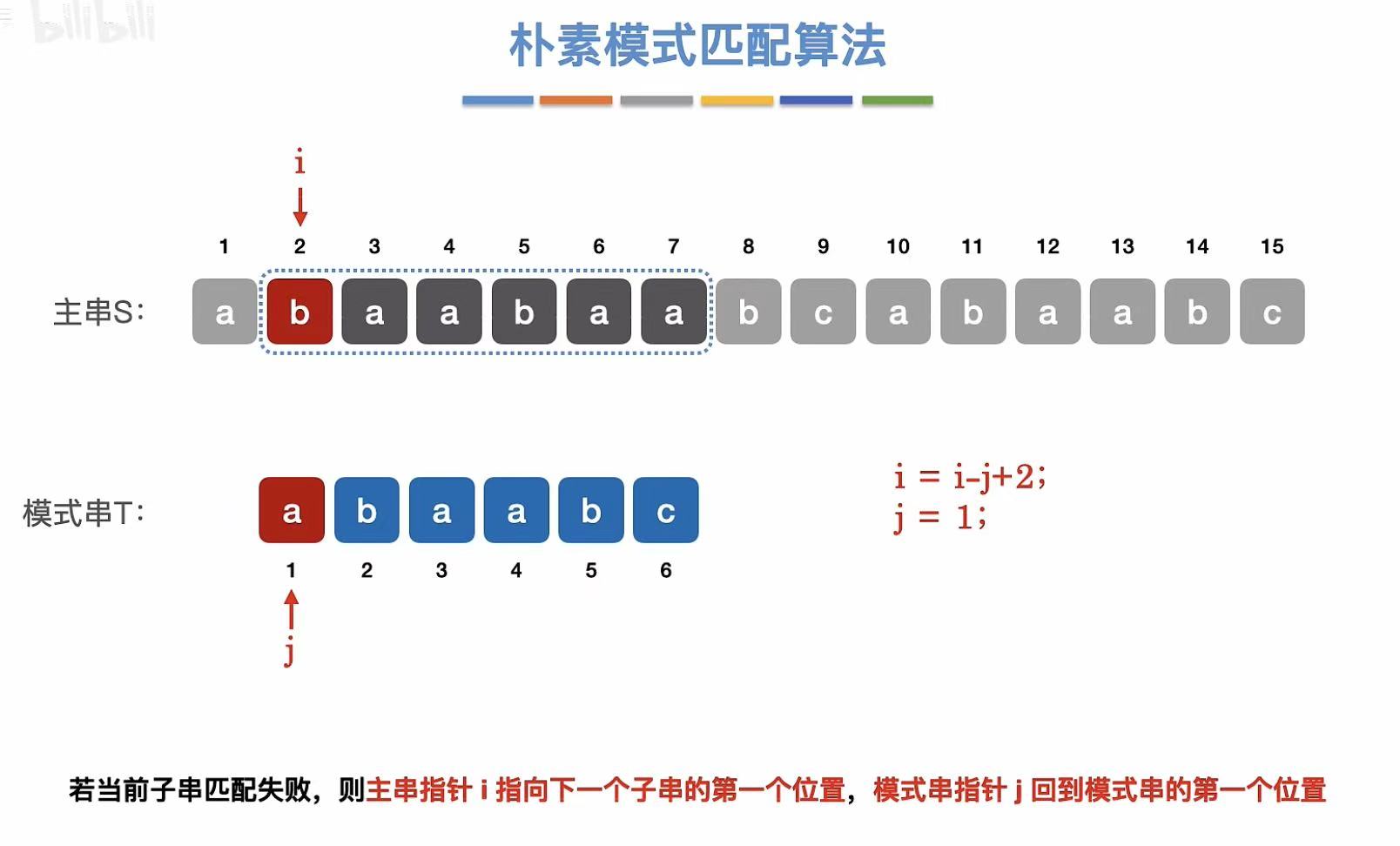
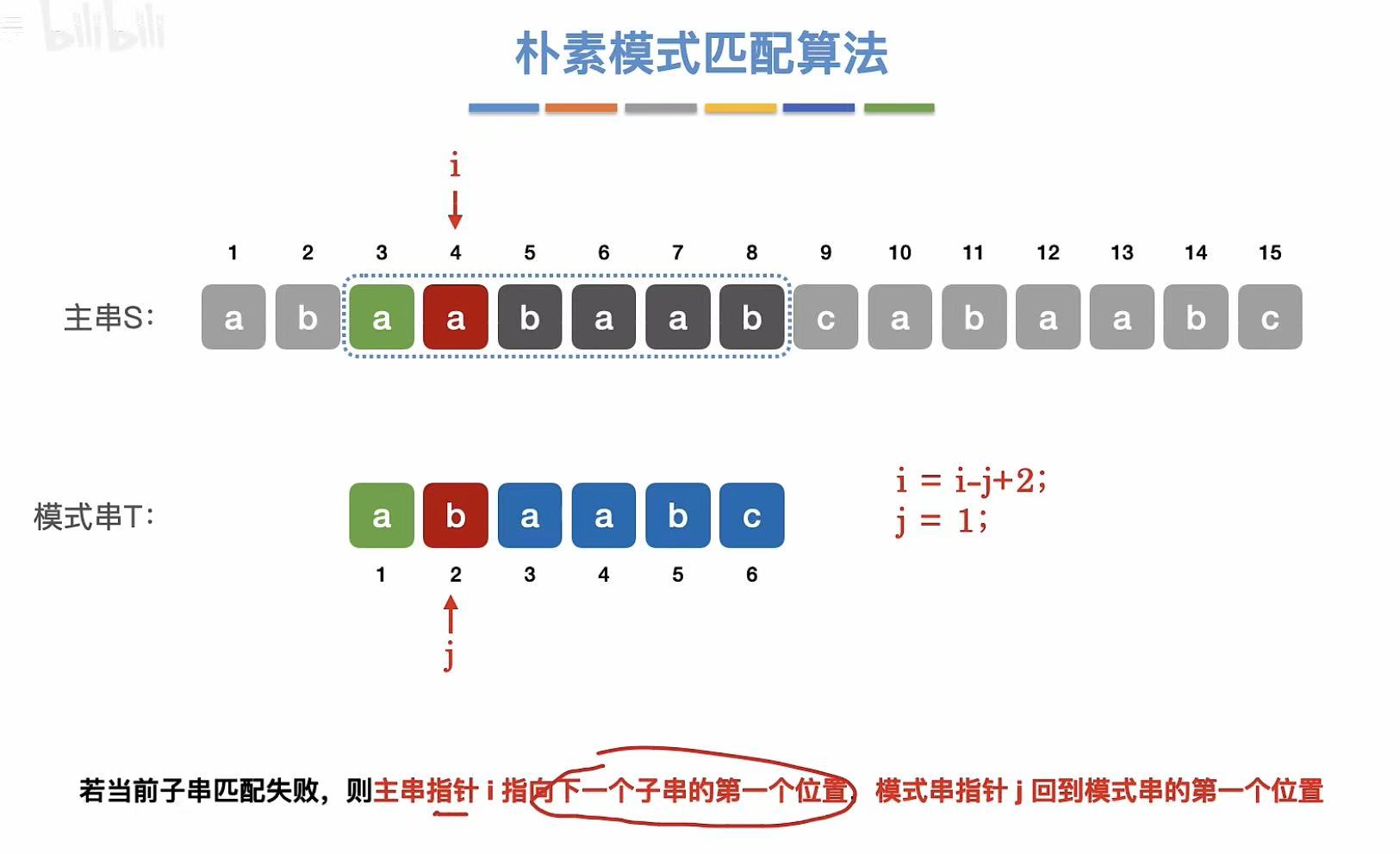
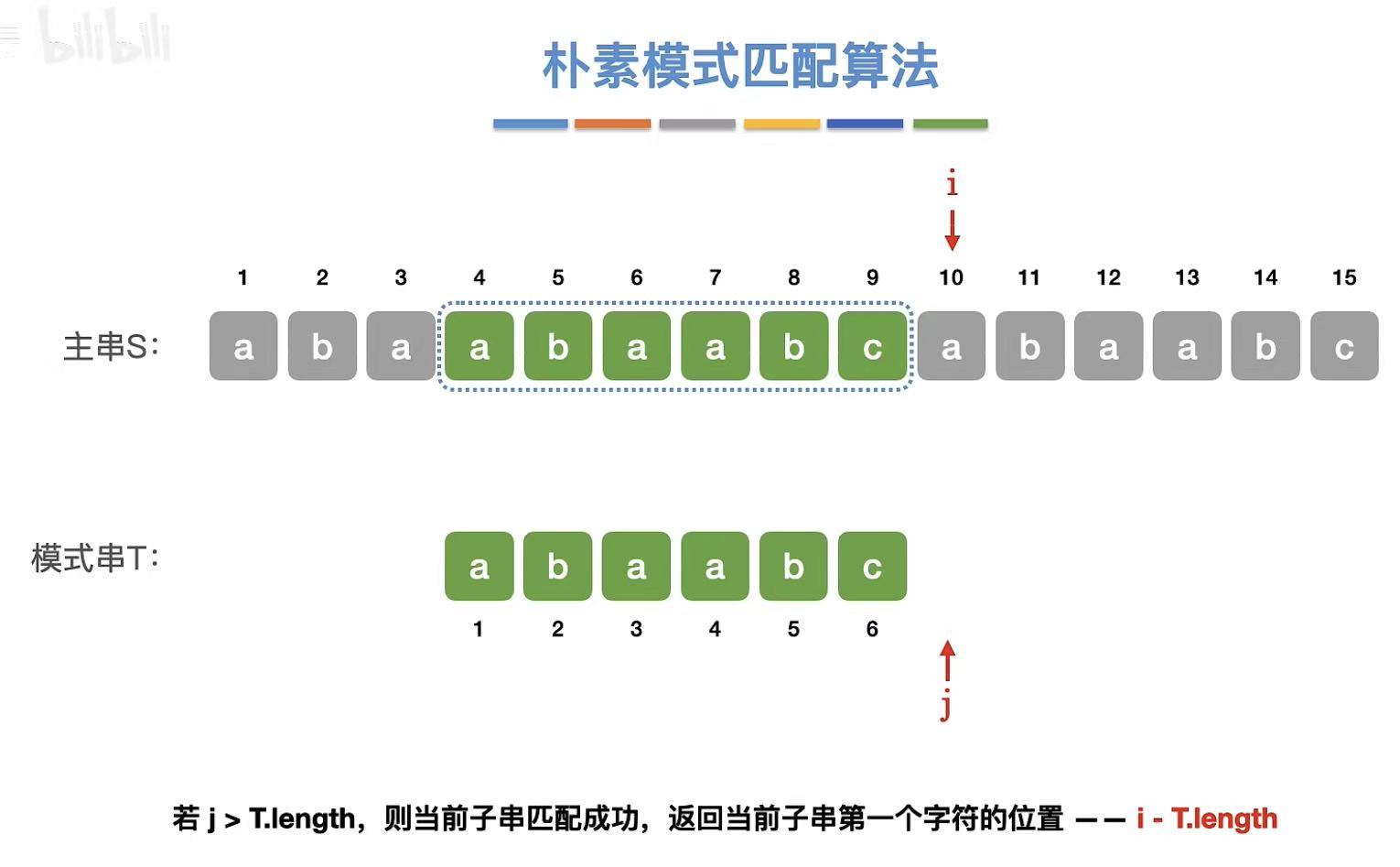
java
// 定位操作:在主串 S 中查找子串 T 第一次出现的位置。
// 若存在,则返回其起始位置(从1开始);否则返回0。
int Index(SString S, SString T) {
// i 是主串 S 的当前比较位置(从1开始)
// j 是模式串 T 的当前比较位置(从1开始)
int i = 1, j = 1;
// 循环条件:只要 i 不超过 S 的长度,且 j 不超过 T 的长度,
// 就继续比较字符
while (i <= S.length && j <= T.length) {
// 如果当前字符相等,则继续比较下一个字符
if (S.ch[i] == T.ch[j]) {
++i; // 主串指针后移
++j; // 模式串指针后移
// 注:这表示"匹配成功,继续往后比"
}
// 如果当前字符不相等,则需要回退并重新开始匹配
else {
i = i - j + 2;
j = 1; // ← 重置模式串指针
// 注:这相当于将主串指针回退到上次匹配的前一个位置
}
}
// 匹配成功判断:如果 j > T.length,说明整个模式串都被匹配完
if (j > T.length)
return i - T.length; // 返回匹配的起始位置
else
return 0; // 未找到匹配,返回0
}
4. 小结
KMP算法
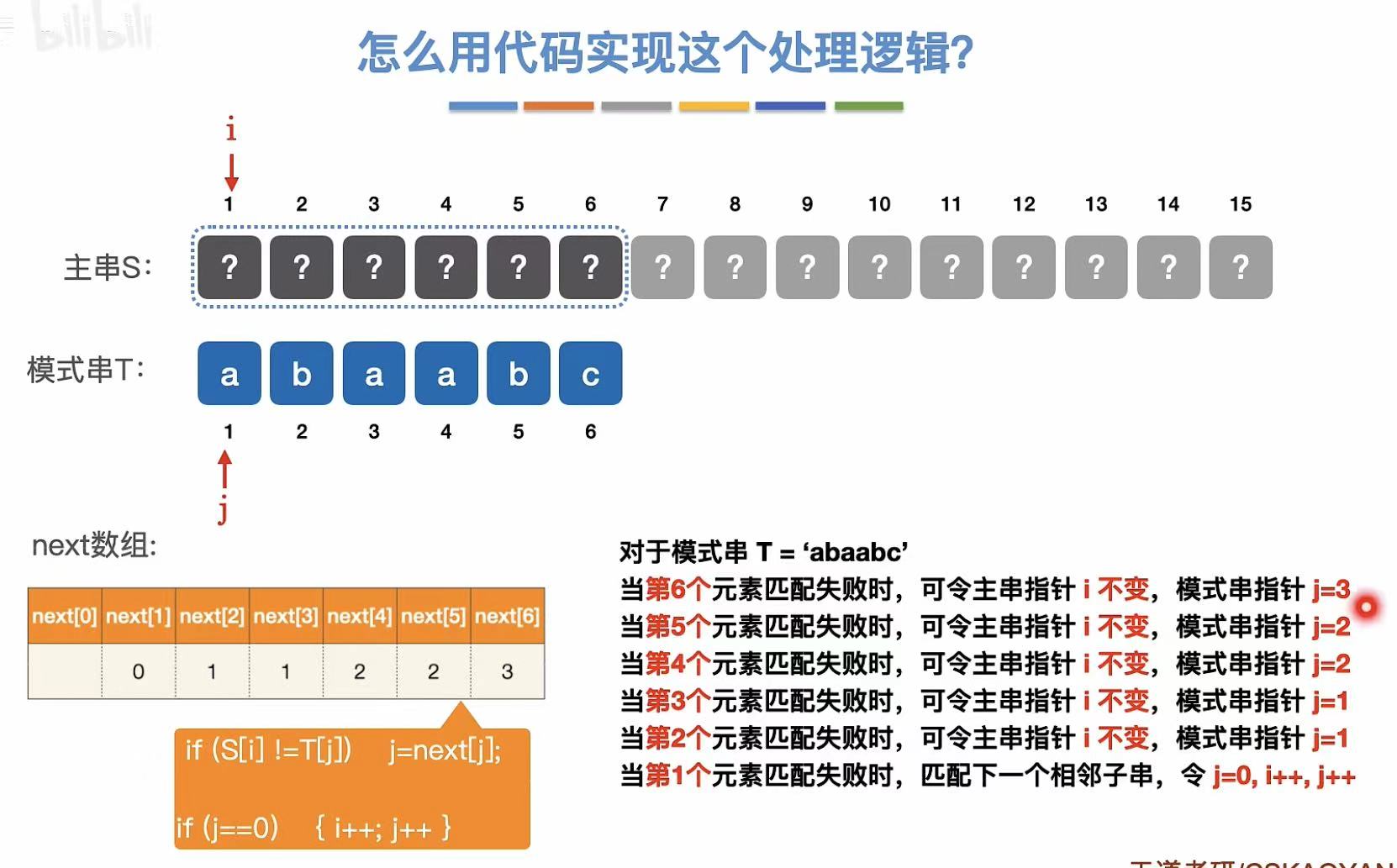
1. 简述

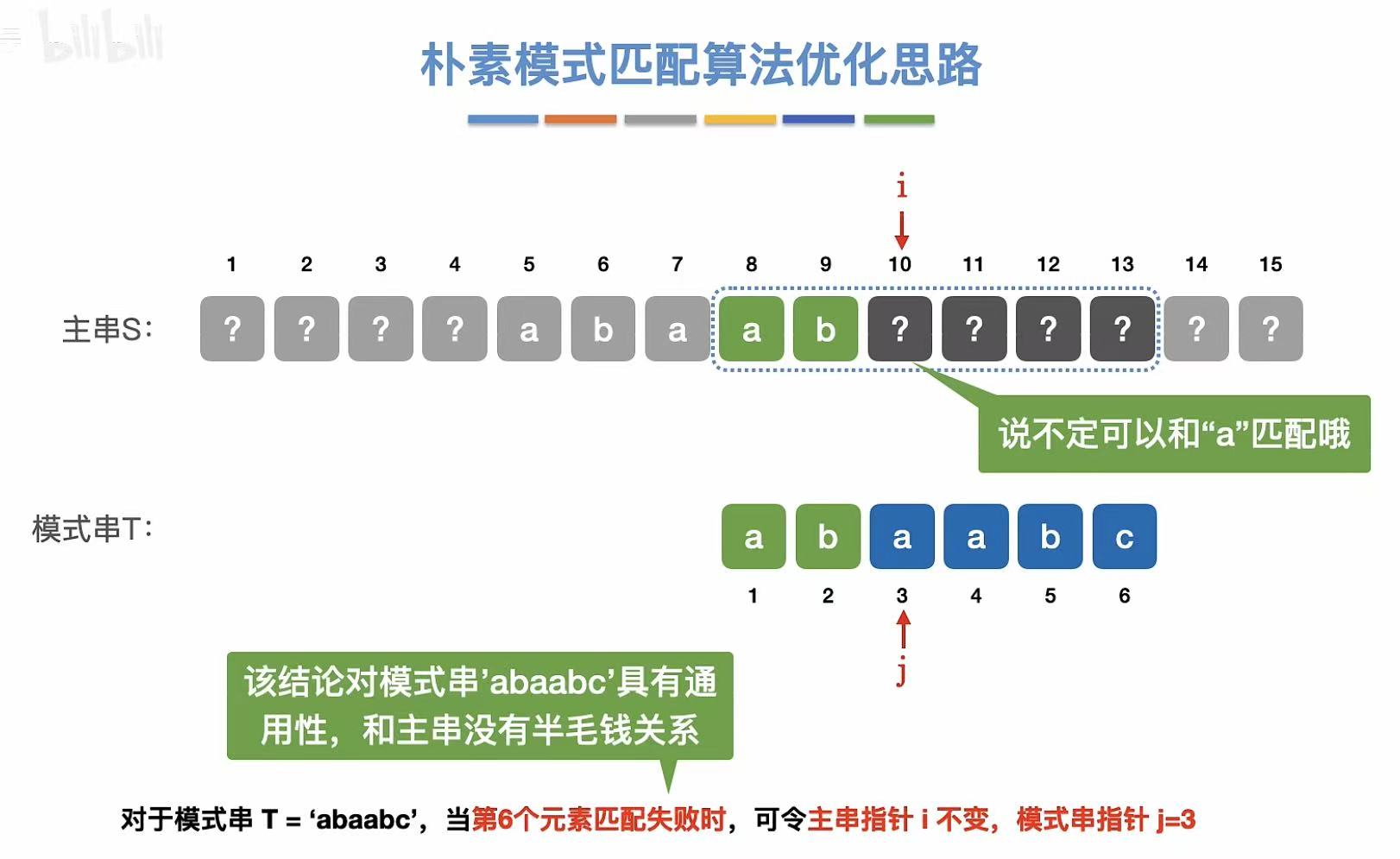
2. 朴素优化思路
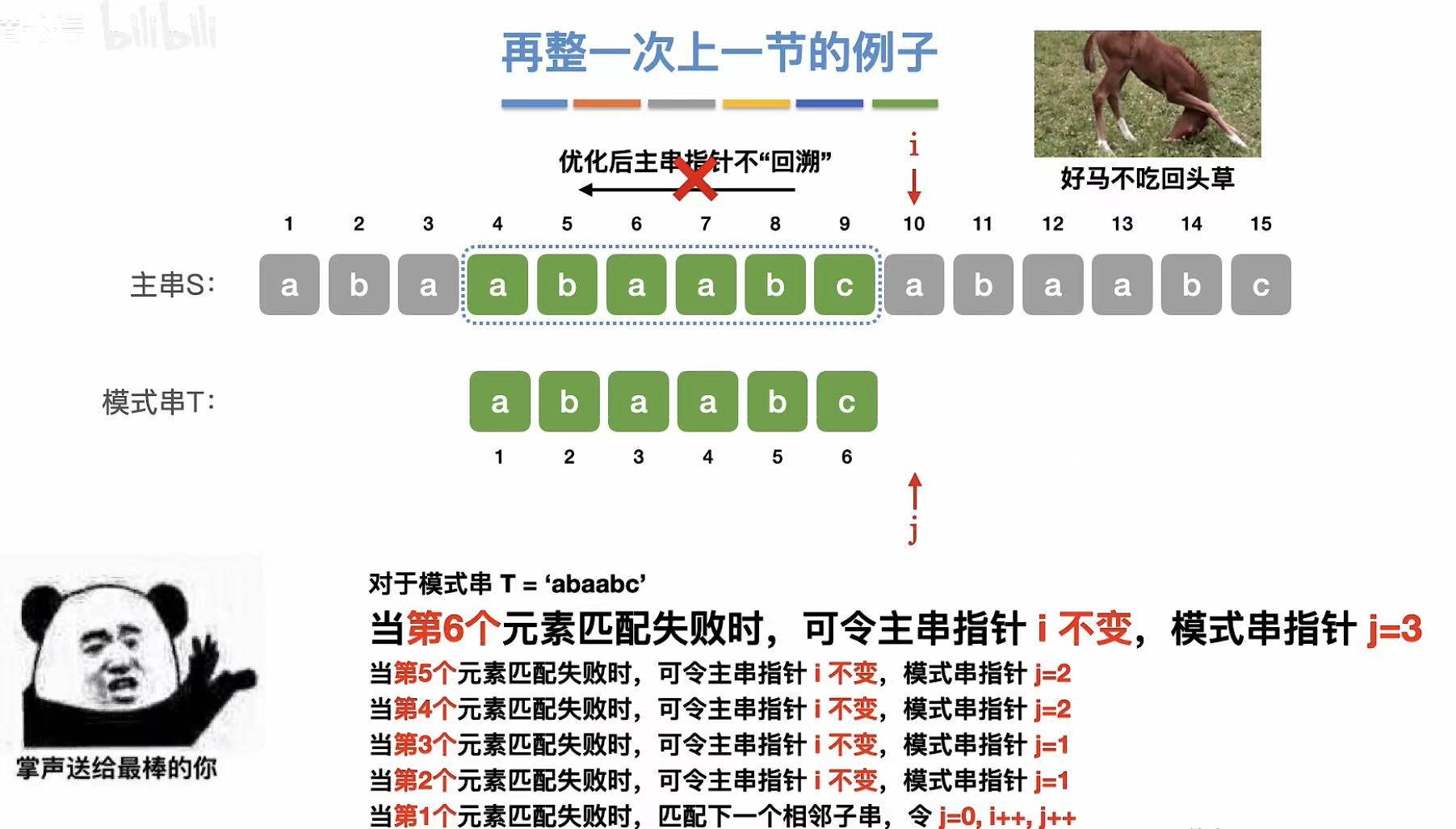
最后一位不匹配,所以就能知道主串之前匹配过的和模式串前面是相同的。
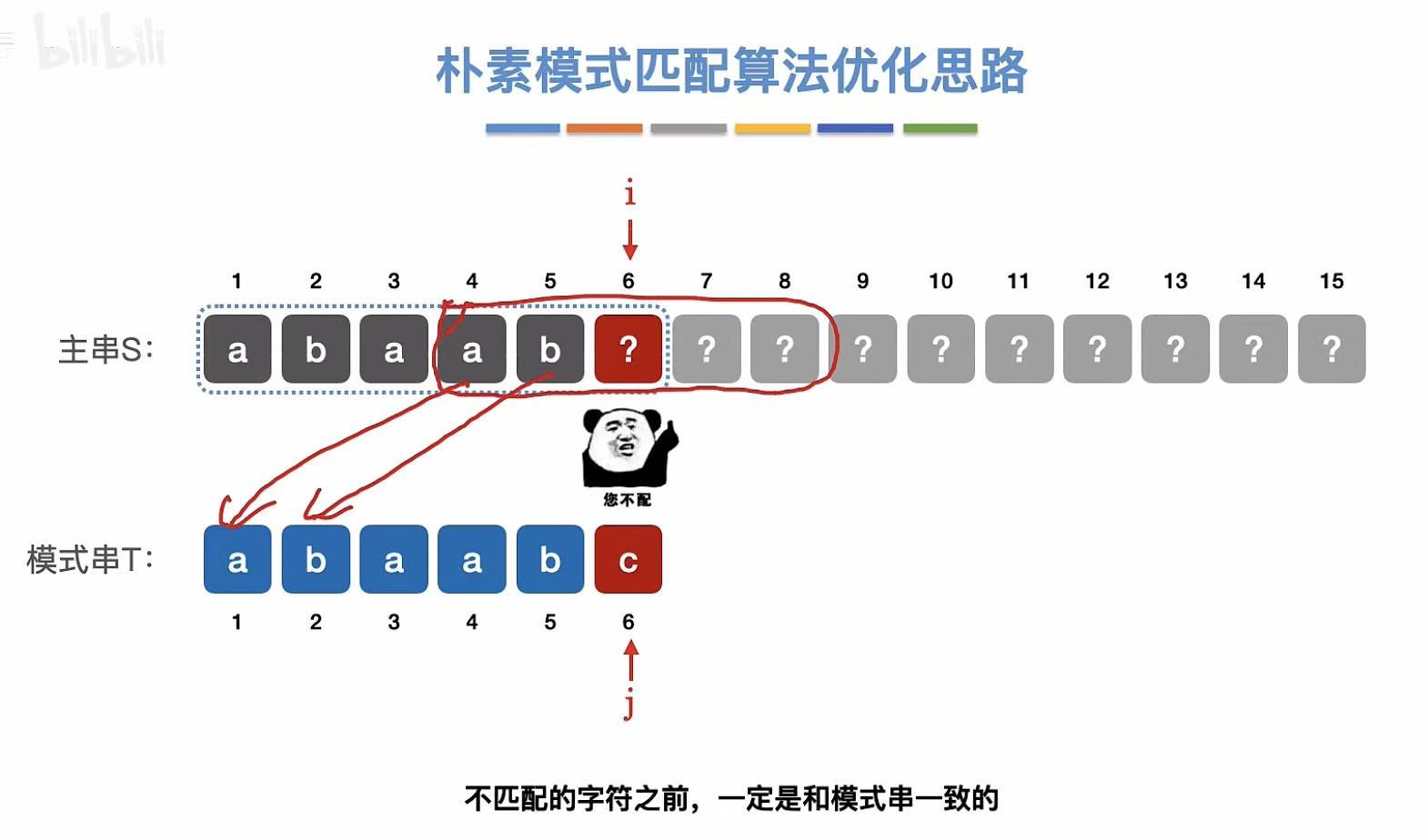
所以就可以跳过已知的不匹配的字母,直接从再次匹配的字母开始进行匹配。
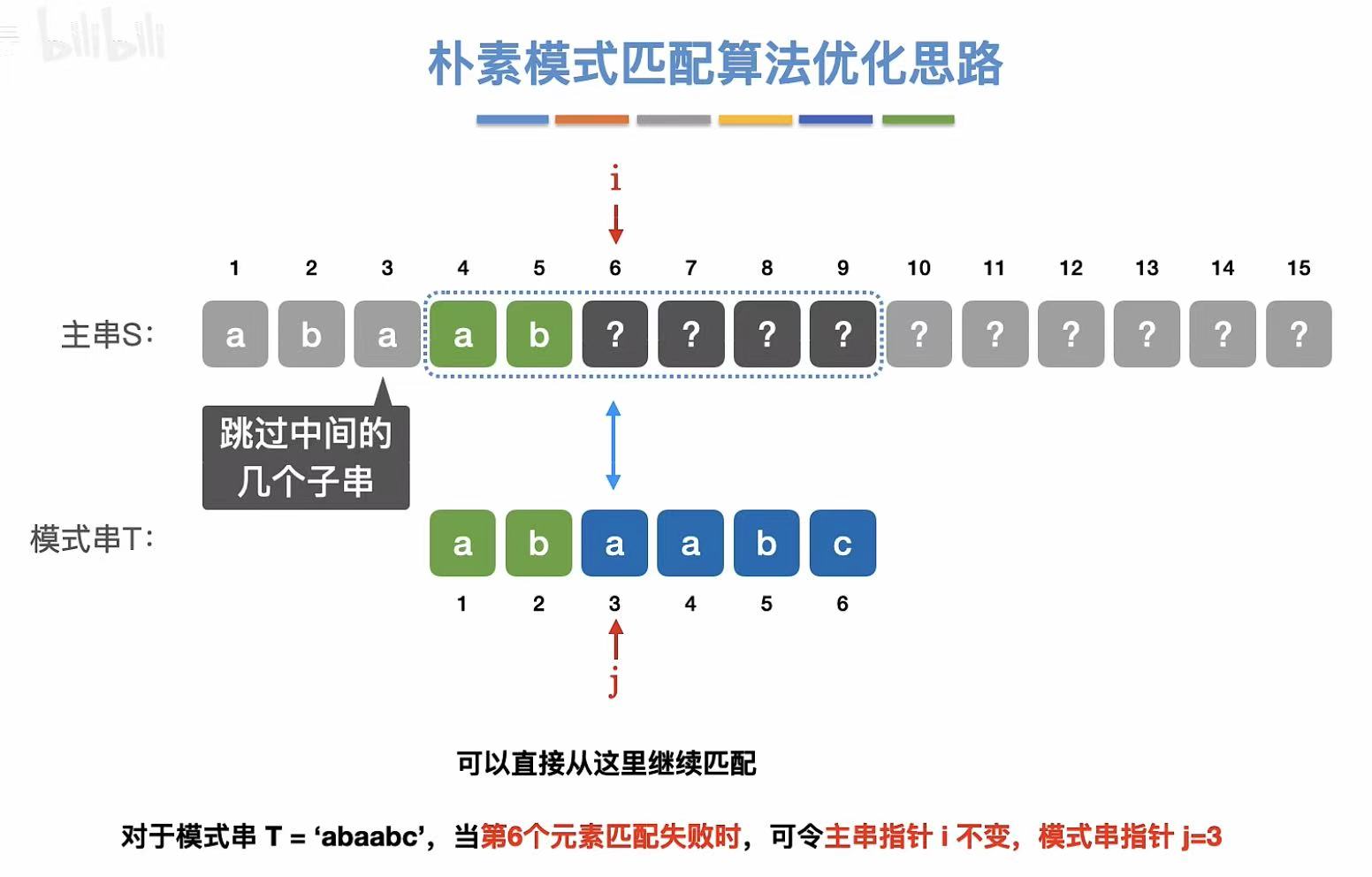
所以,到了主串中不匹配的地方,指向主串的指针不需要移动,但是指向模式串的指针需要进行修改。
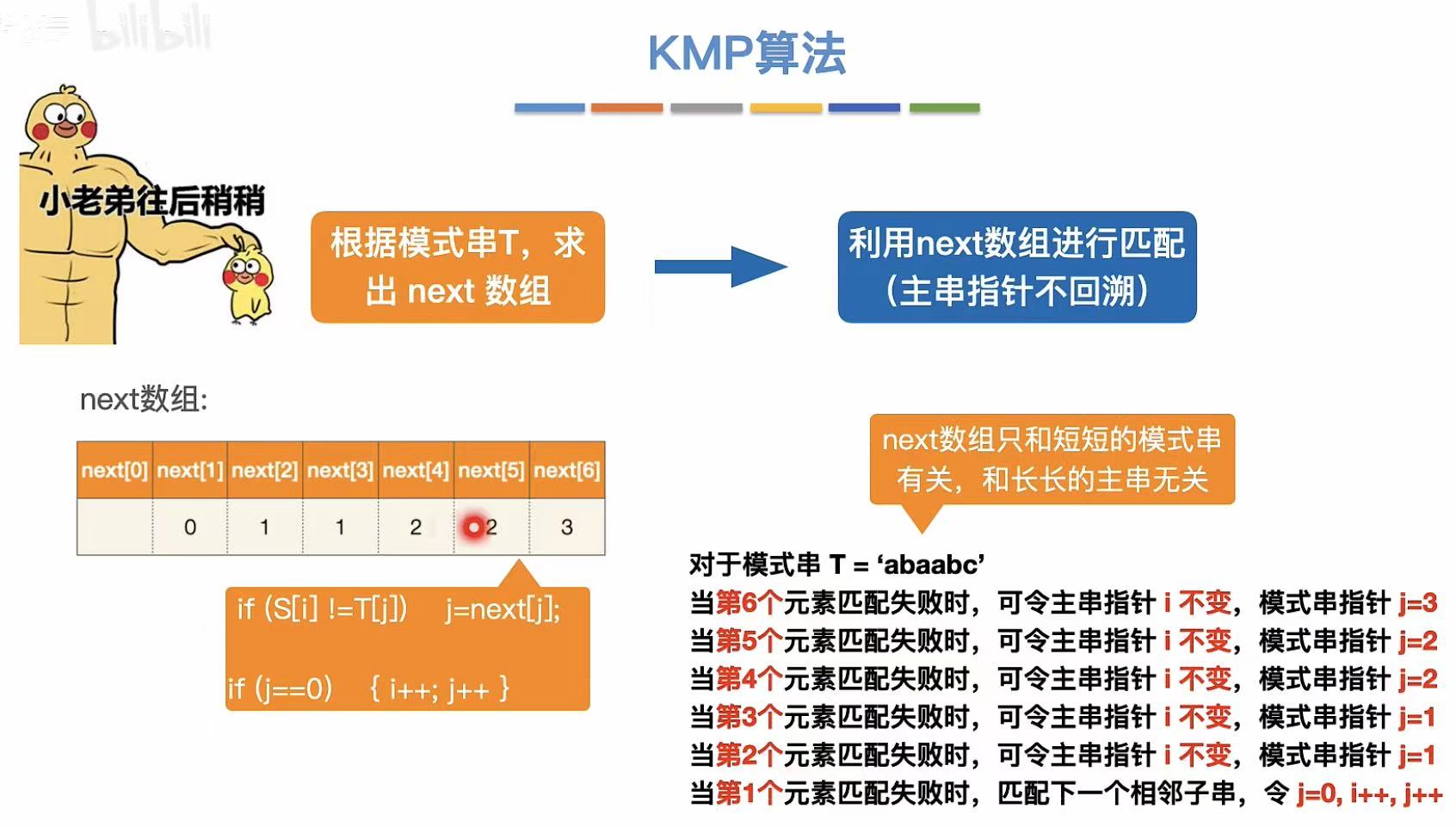
由此可见 :KMP算法和主串没有半毛钱关系,只和模式串有关系。
3. 其他位置
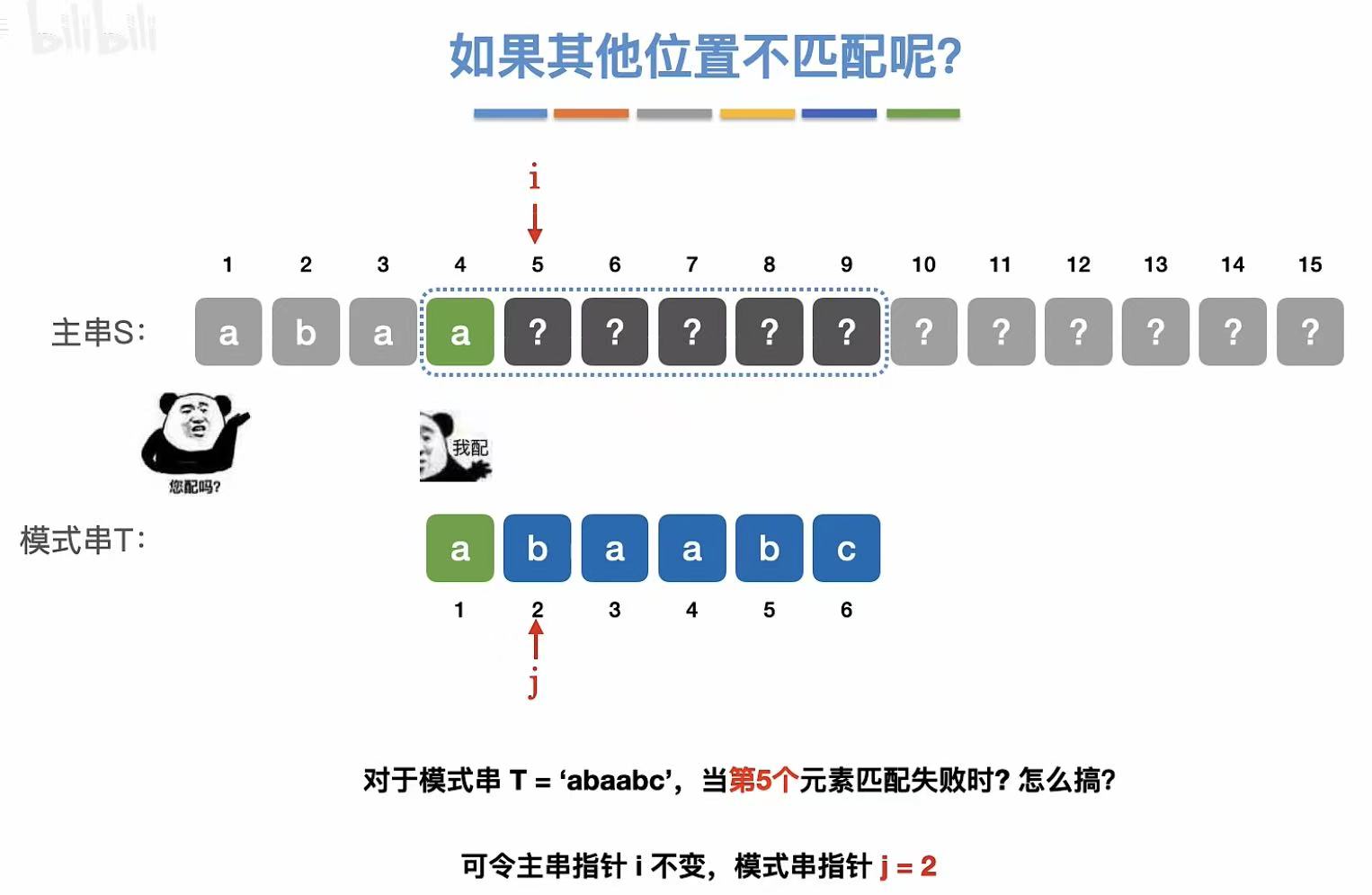
第五个元素不匹配:
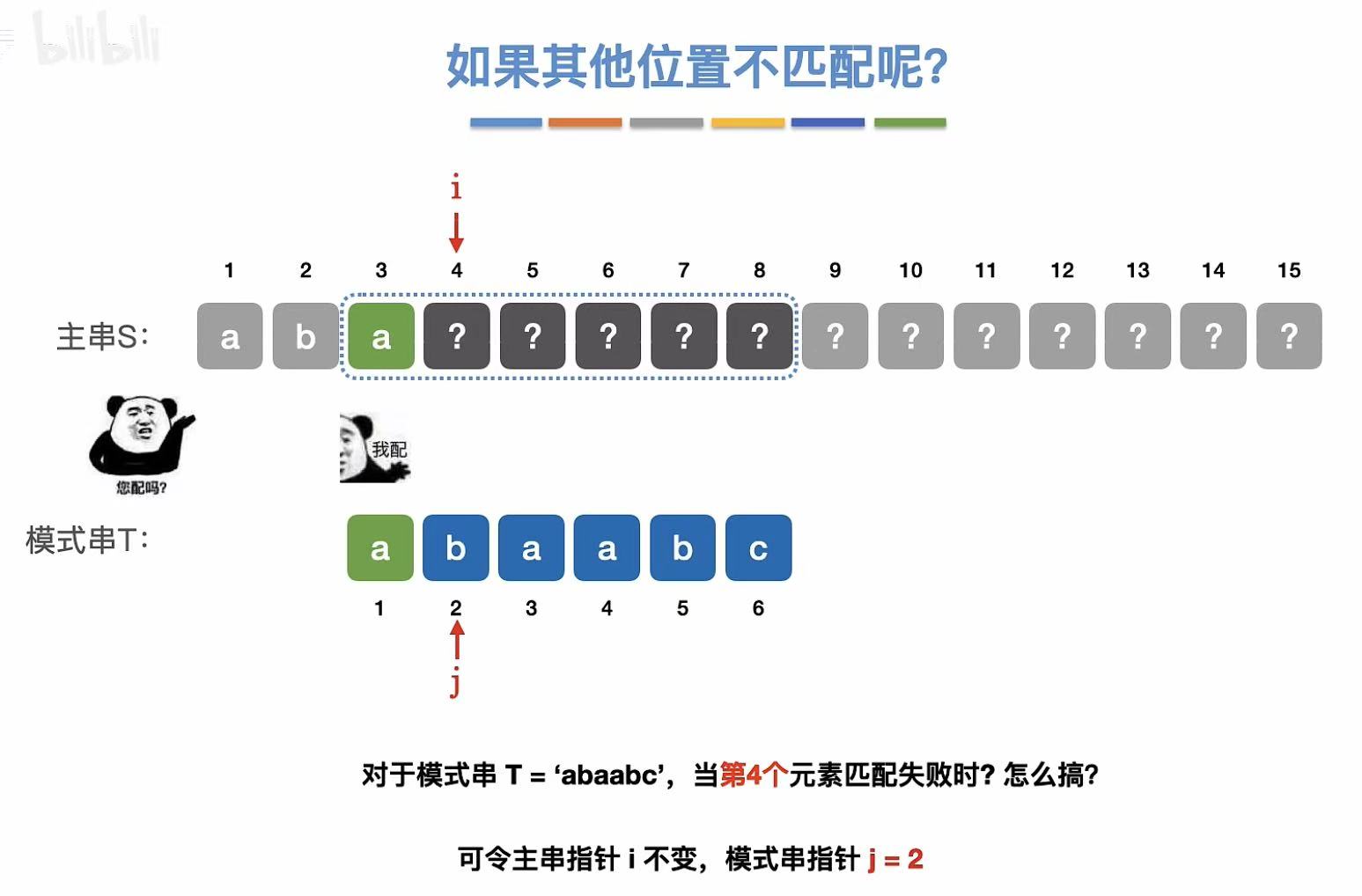
第四个元素不匹配:
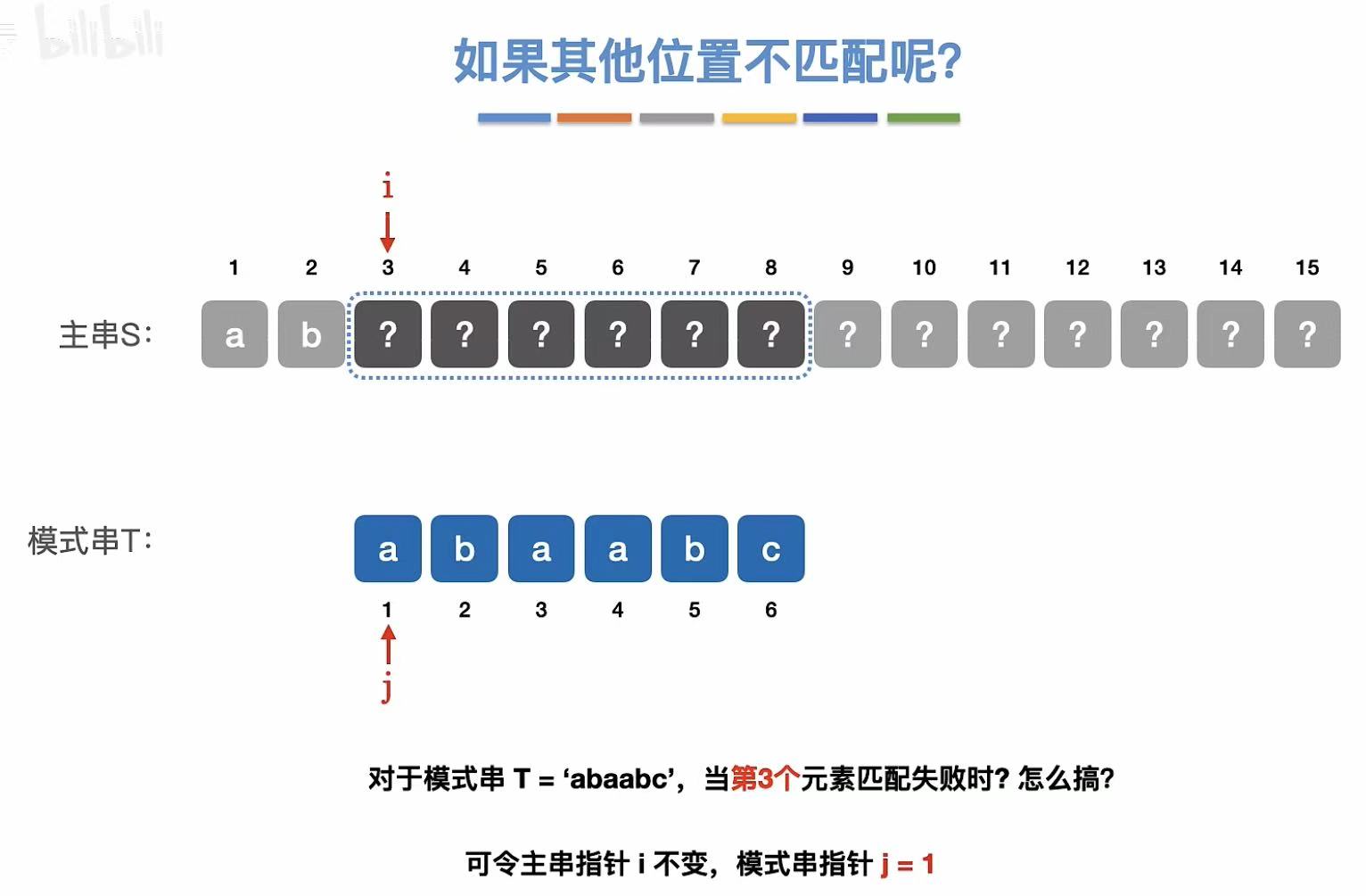
第三个元素不匹配:
第二个元素不匹配:
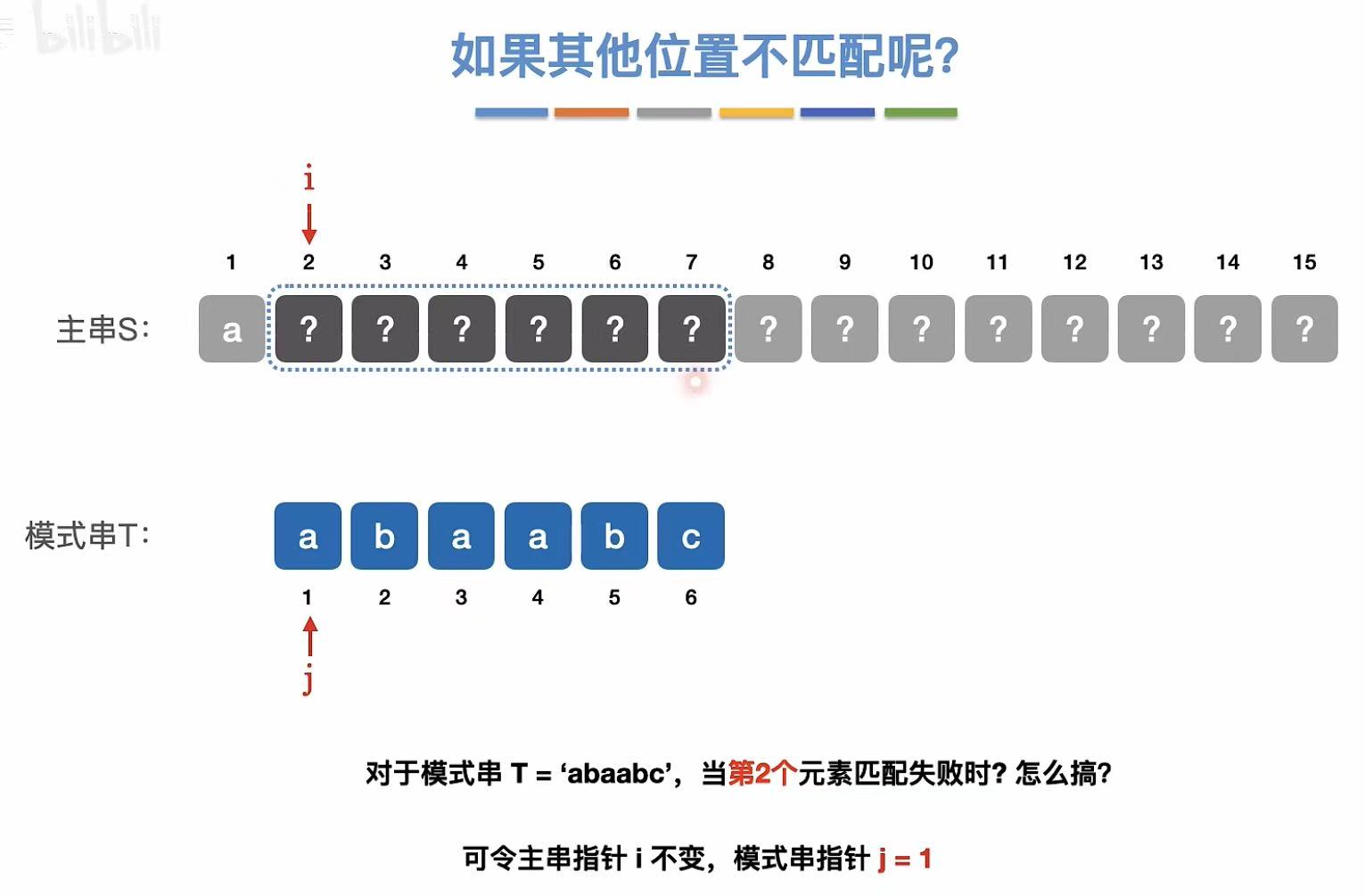
第一个元素不匹配:
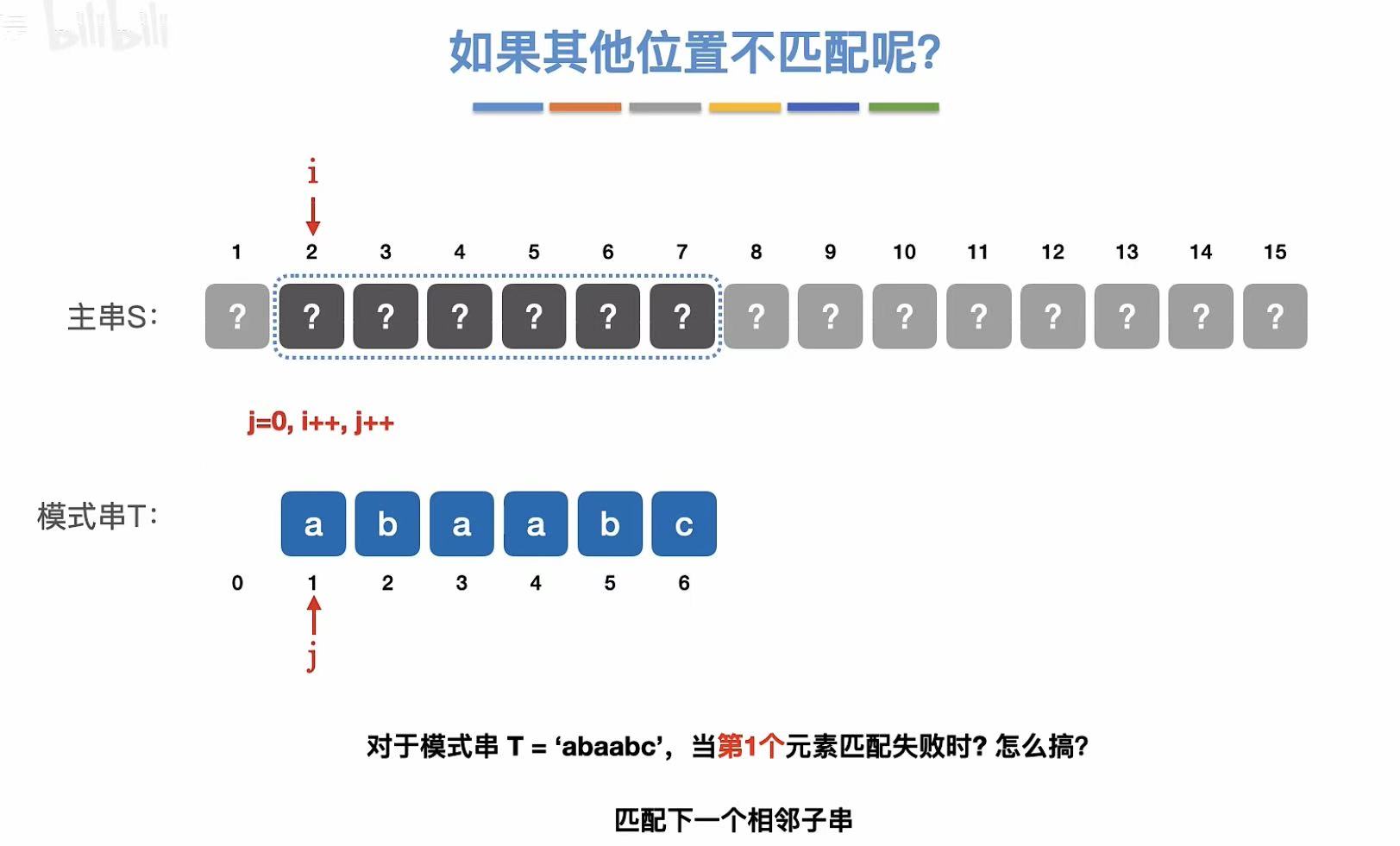
4. 结论
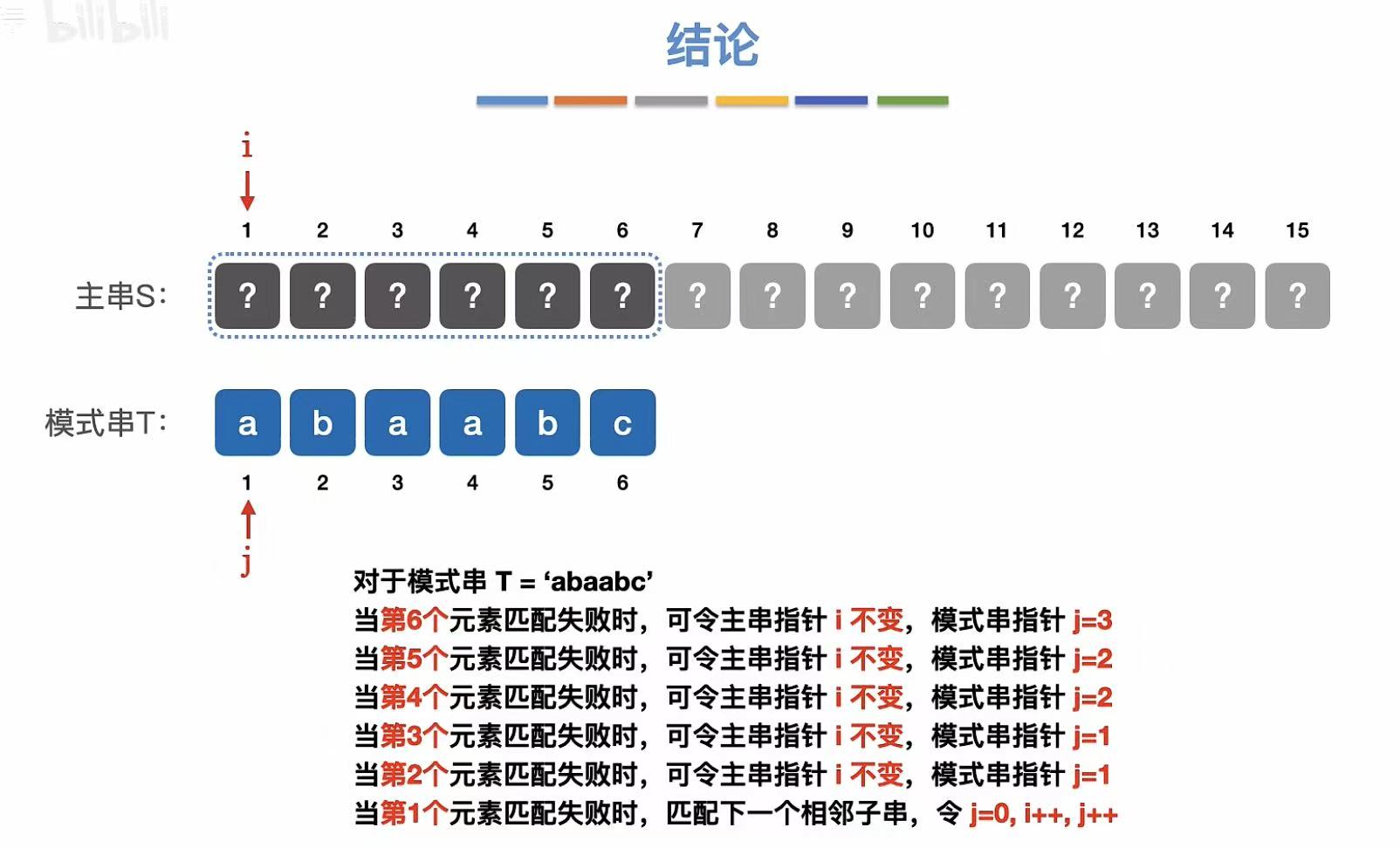
5. 例子
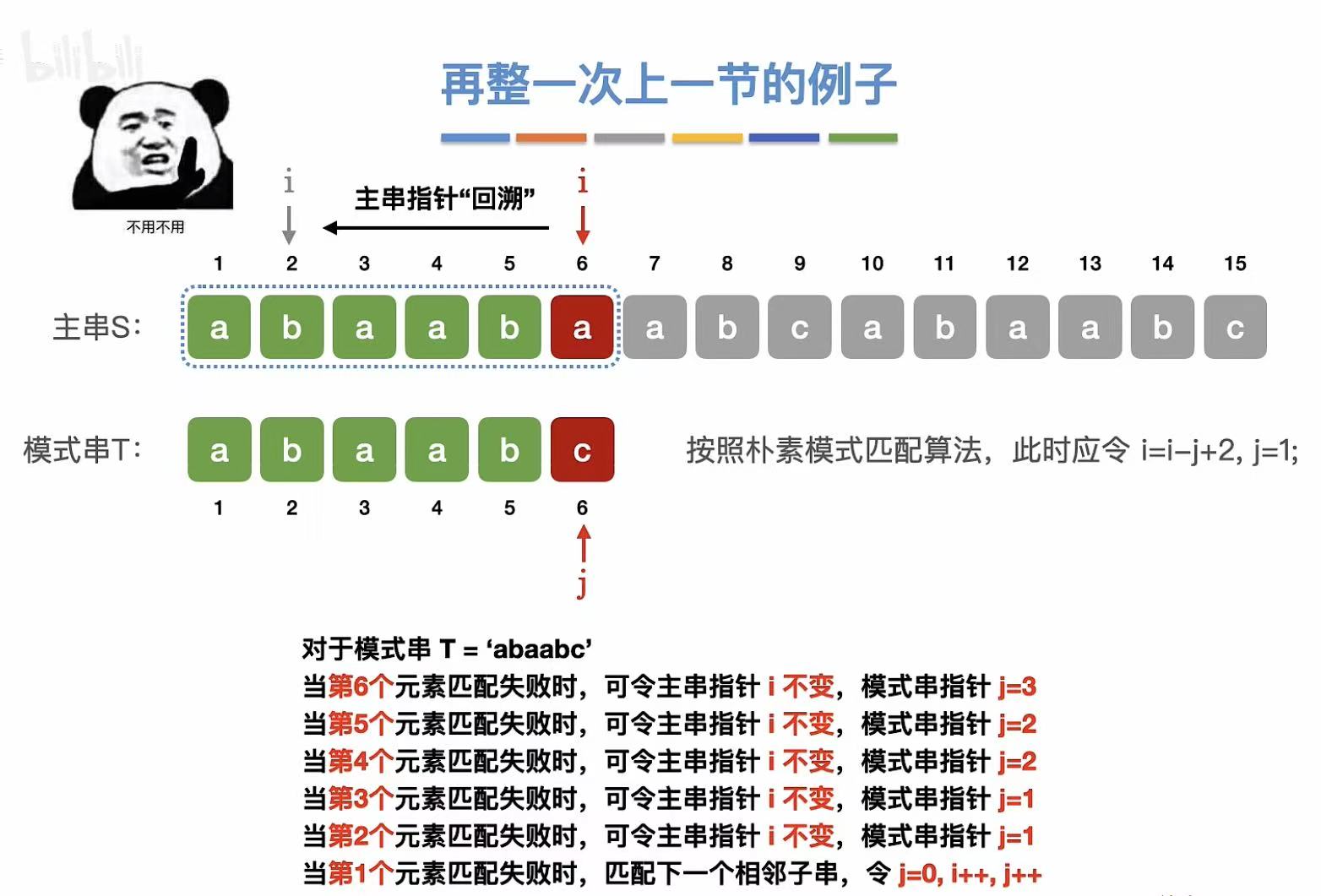
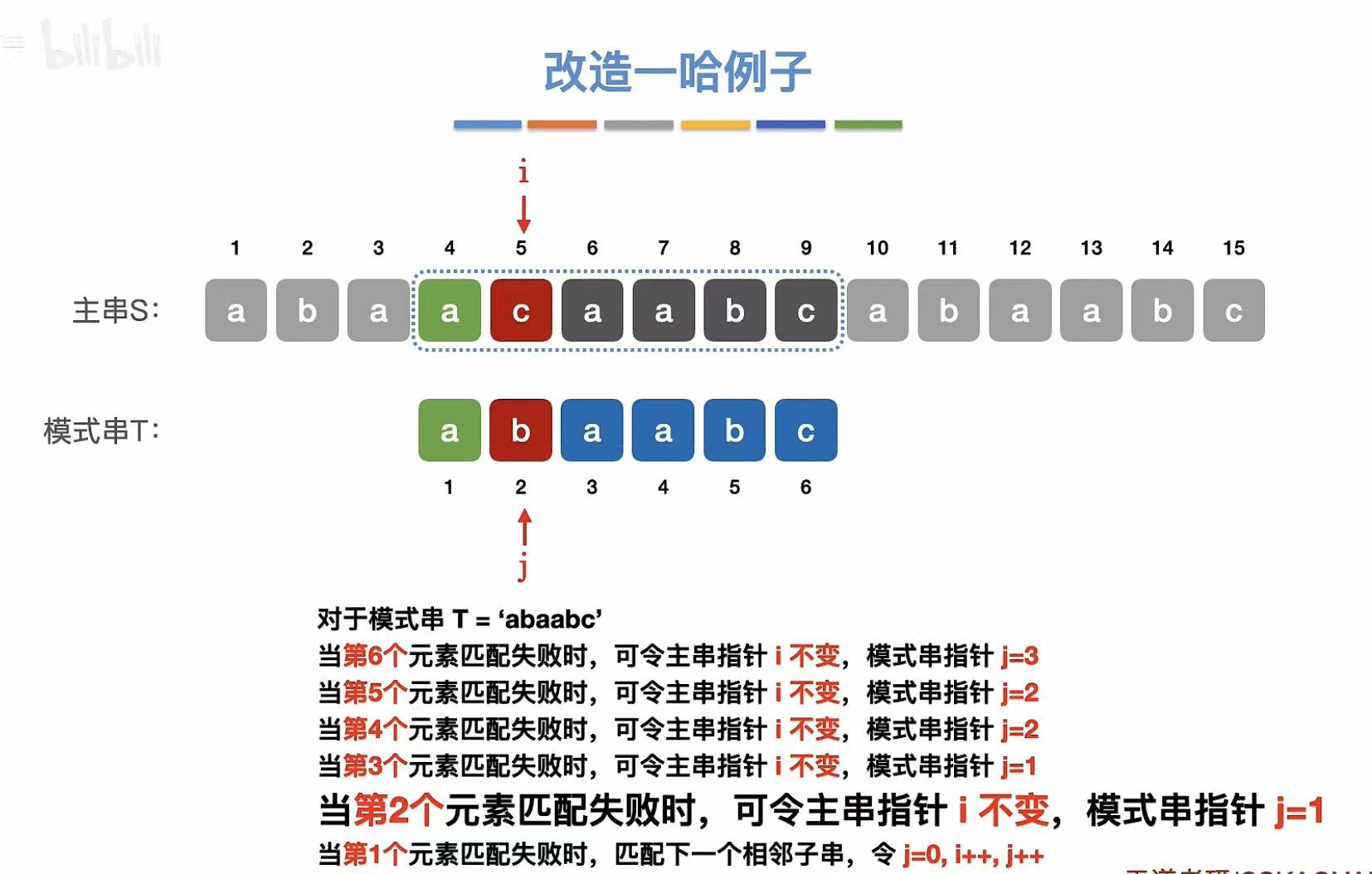
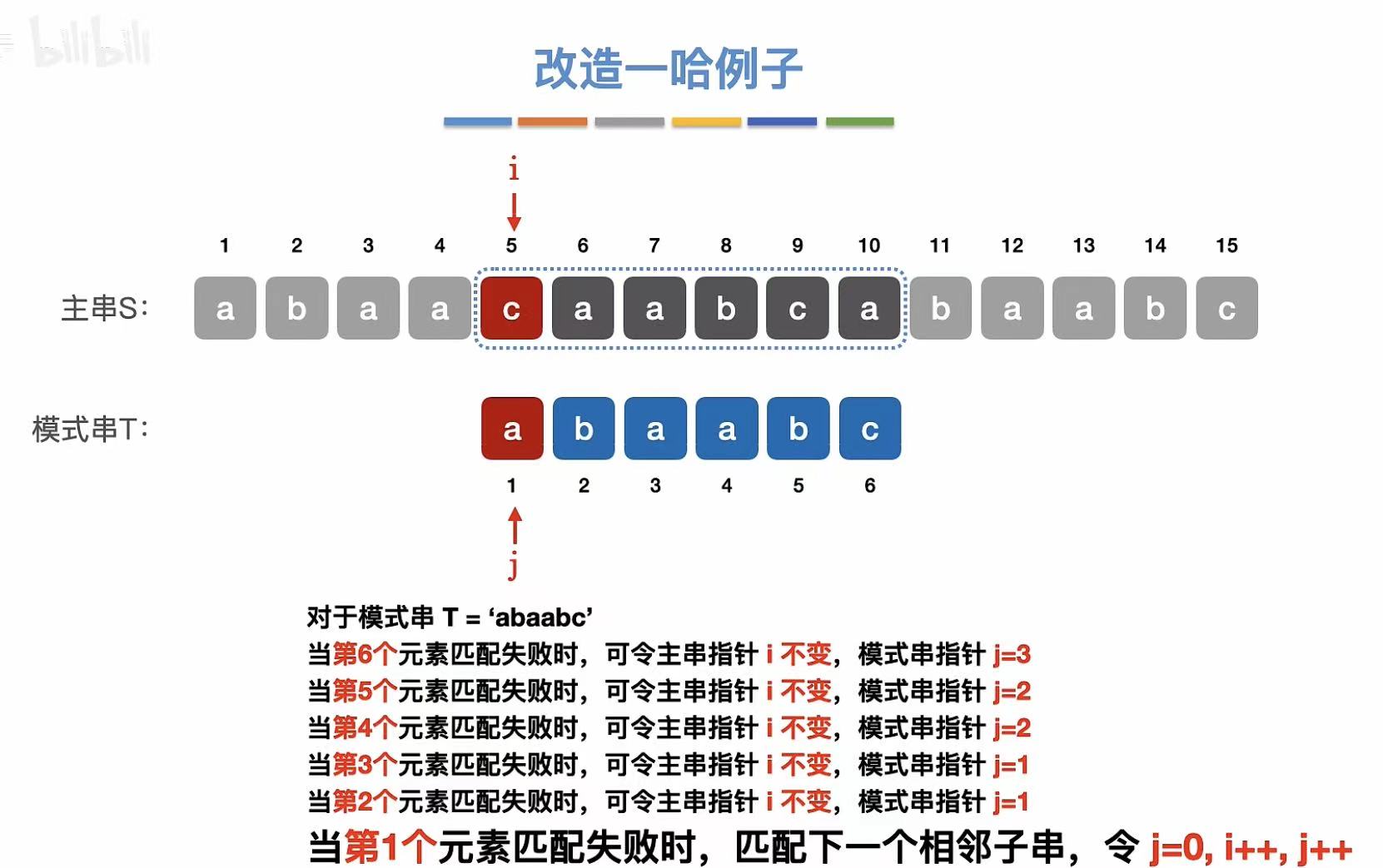
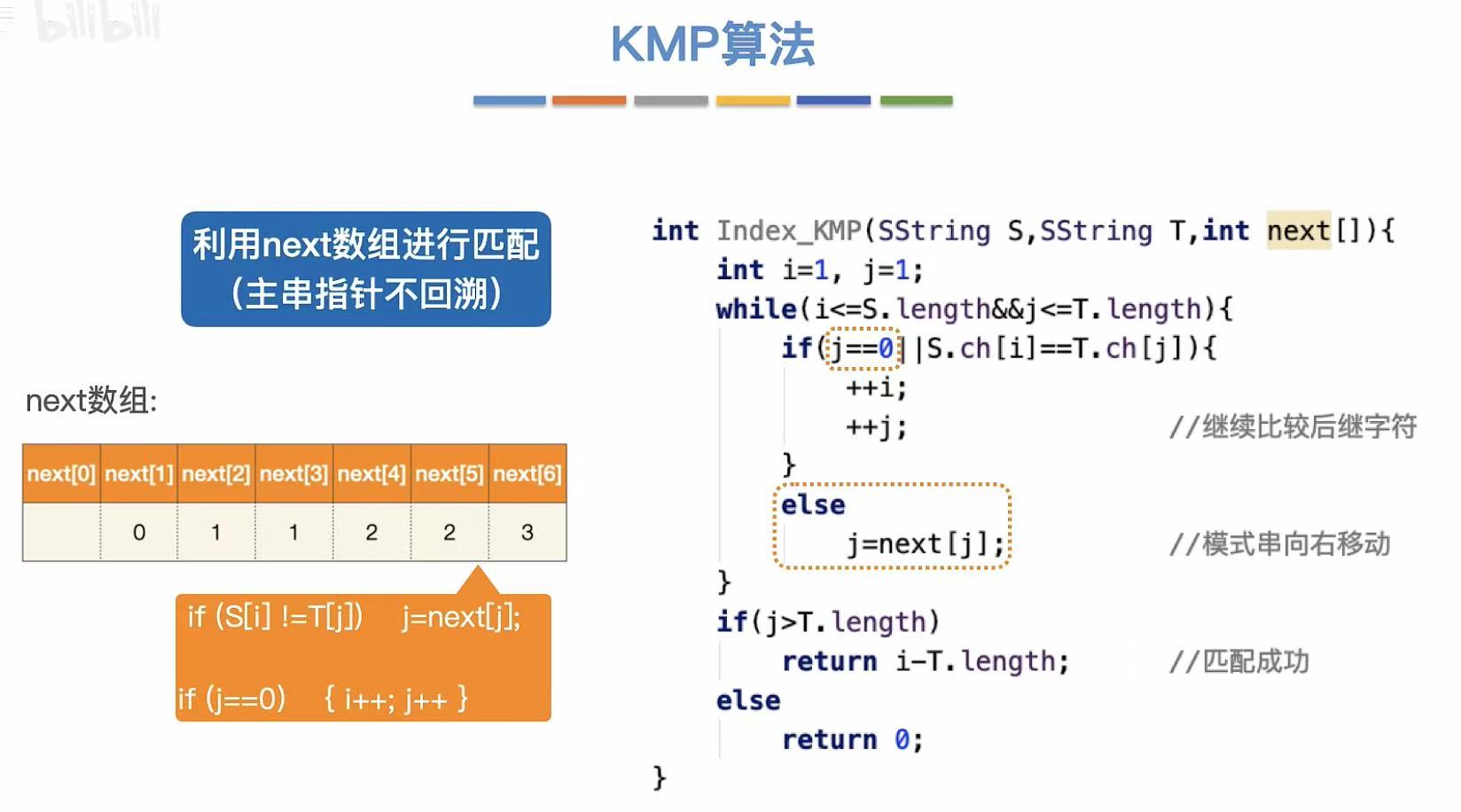
6. 代码实现
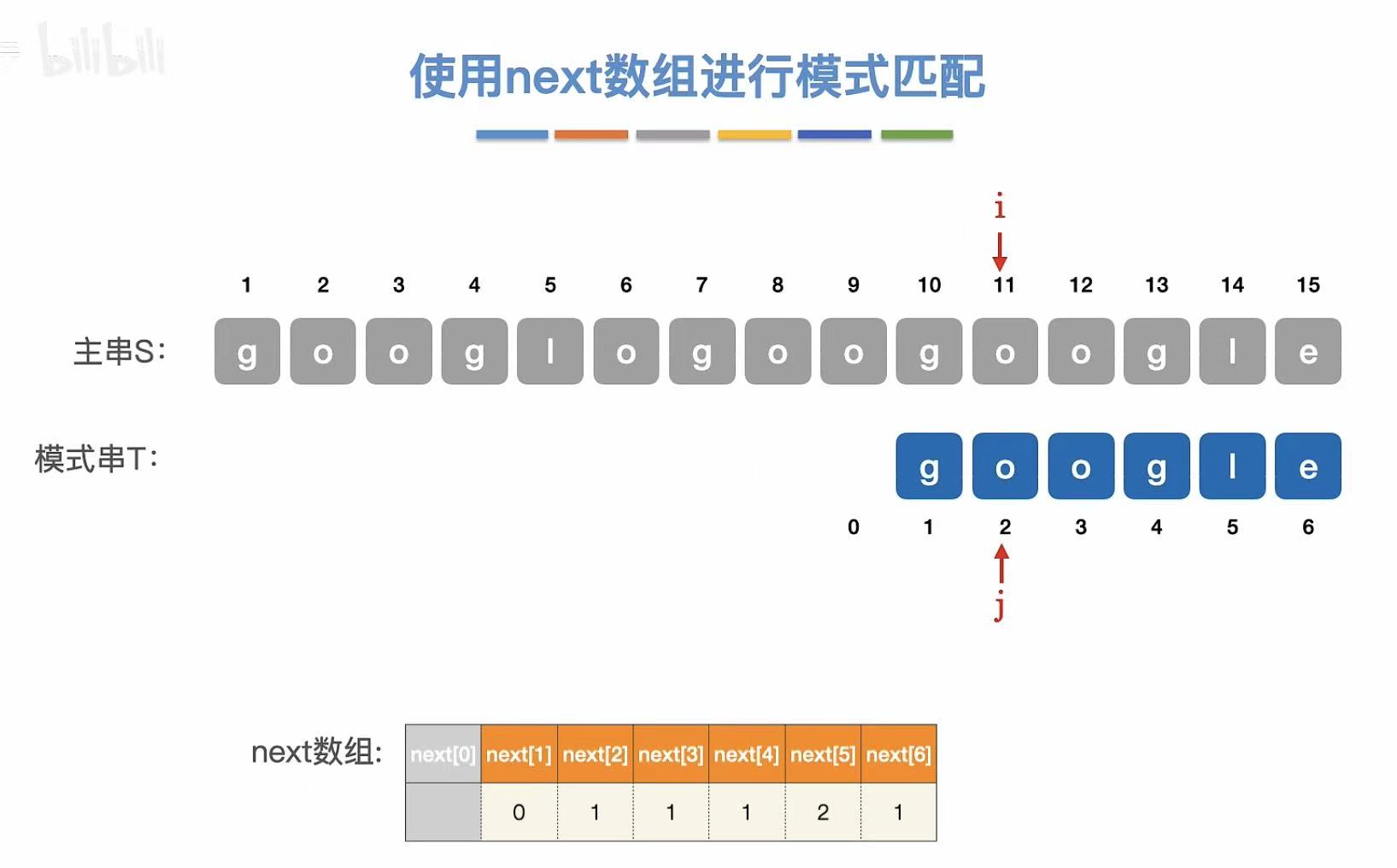
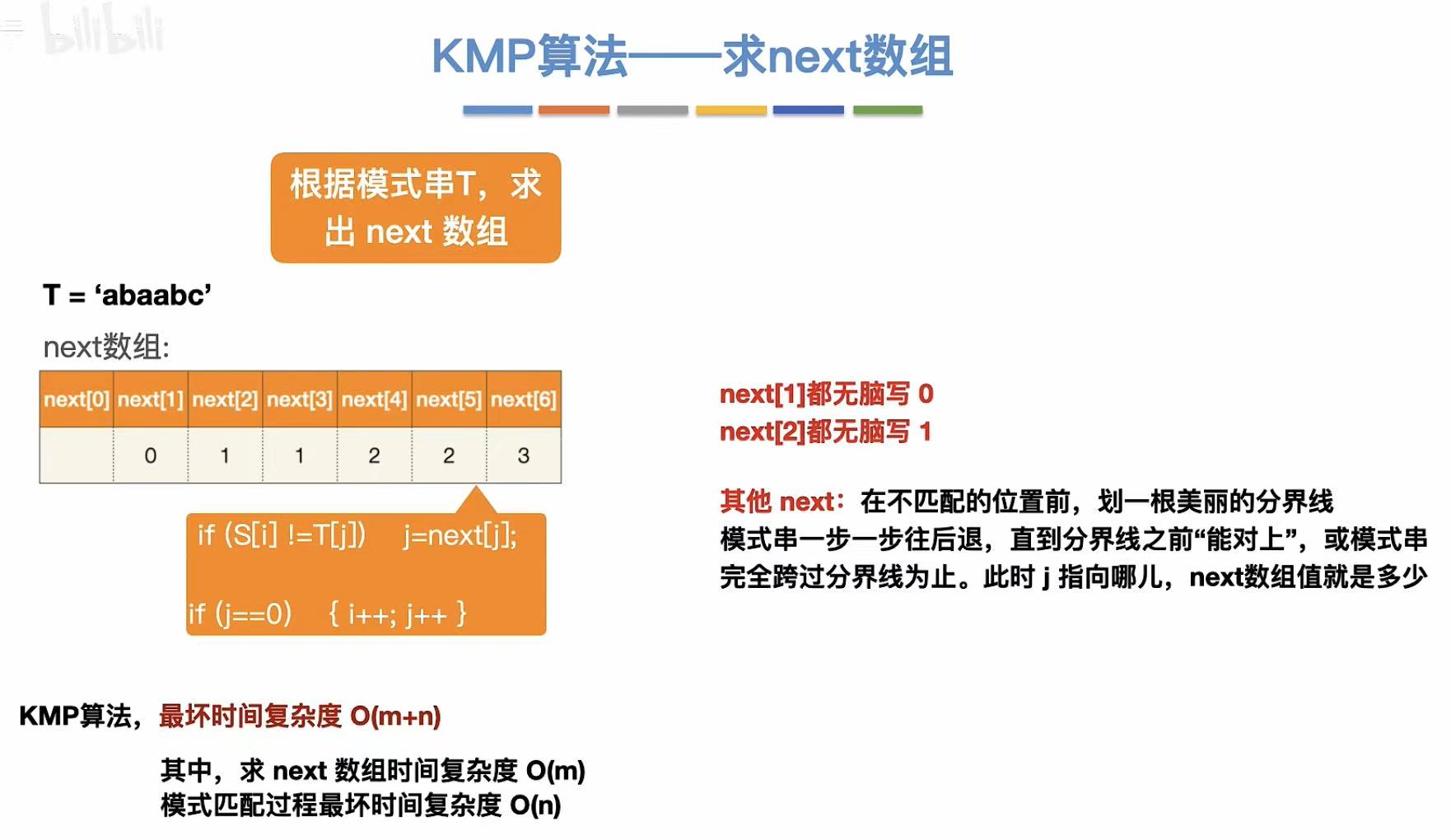
这里就引入了next数组,next[6]就是第六个元素不匹配的话,j指针需要指向模式串的几号位置。
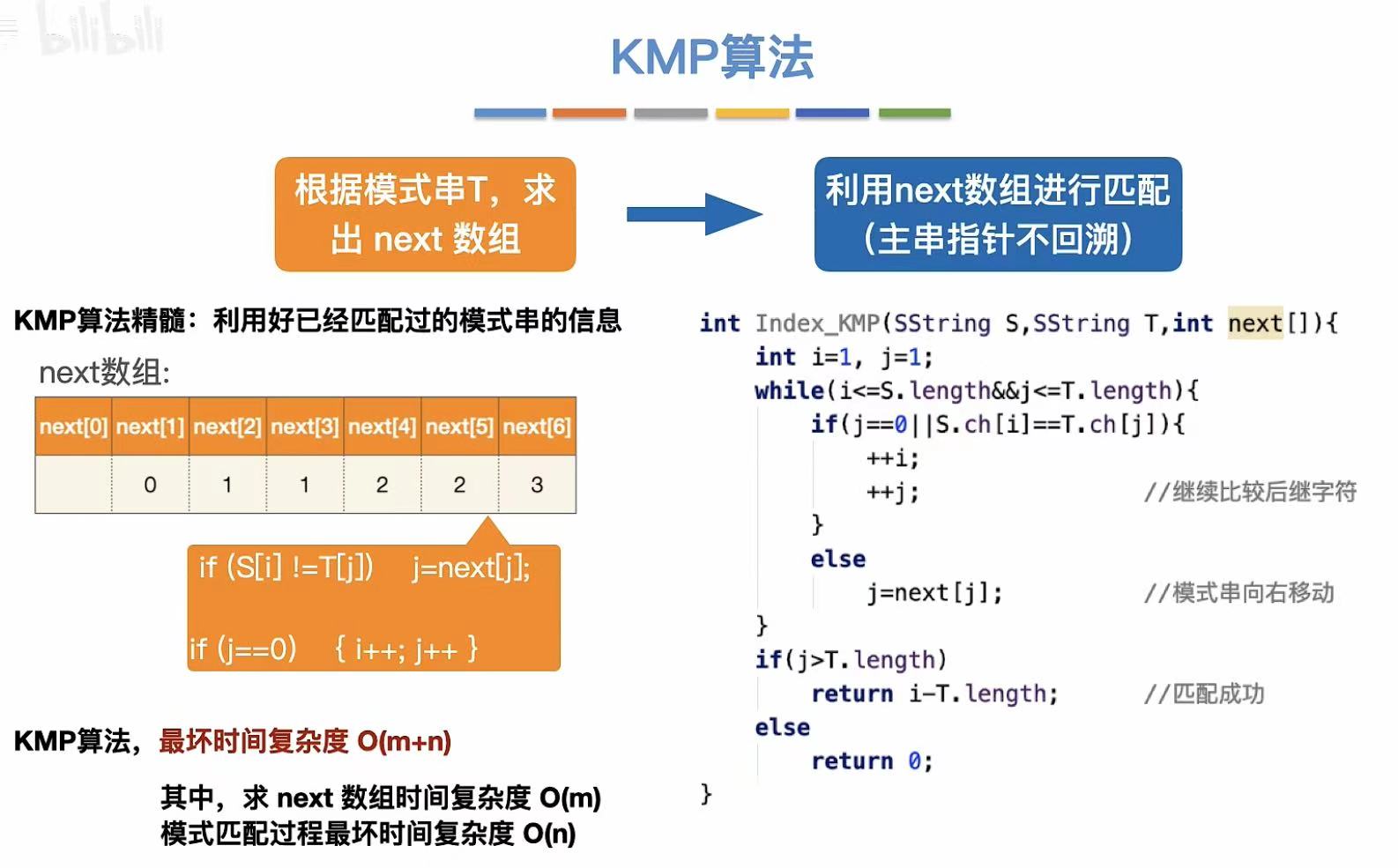
求next数组
1. 练习1
- next[1]:无脑写0
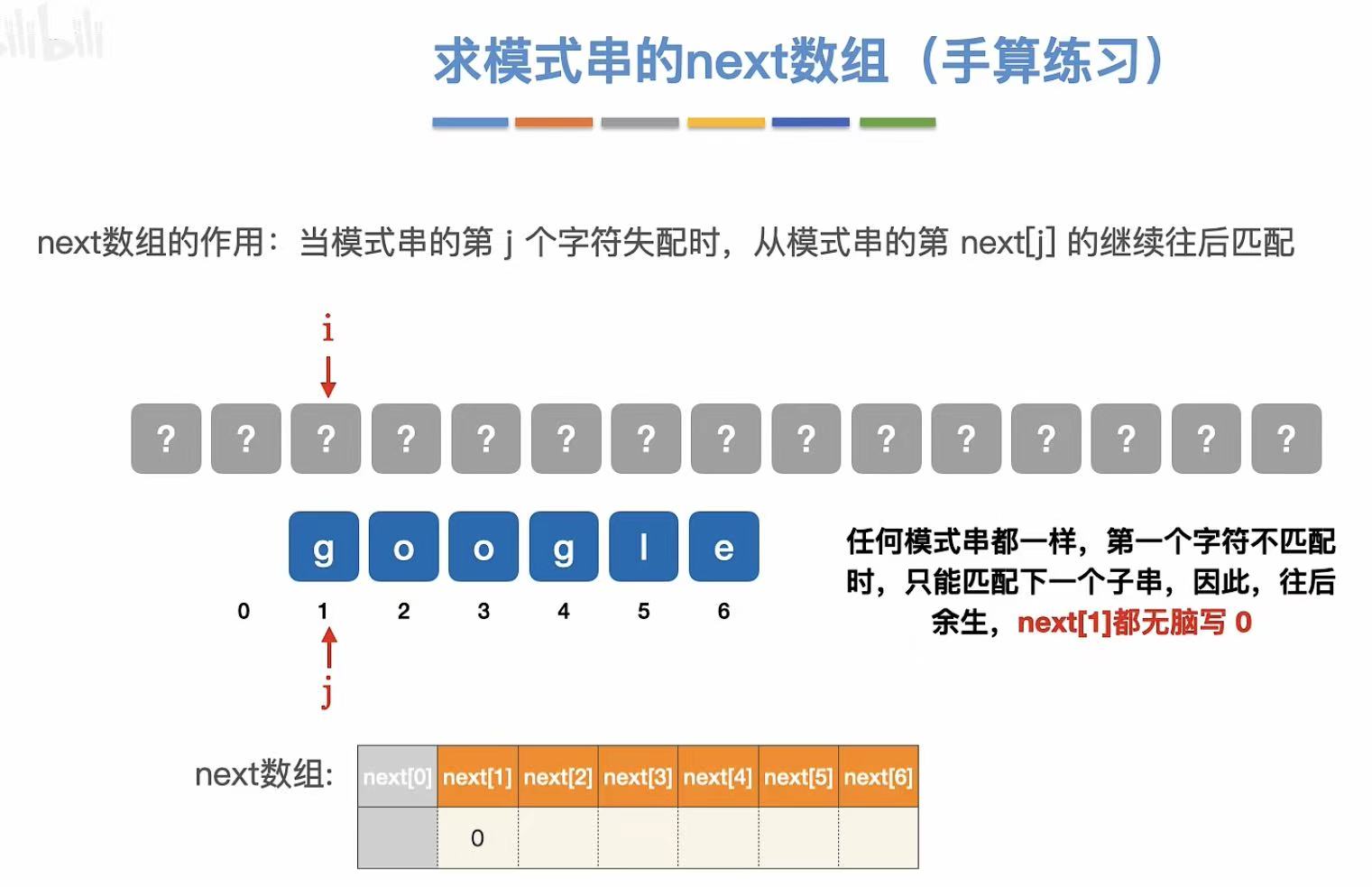
- next[2]:无脑写1
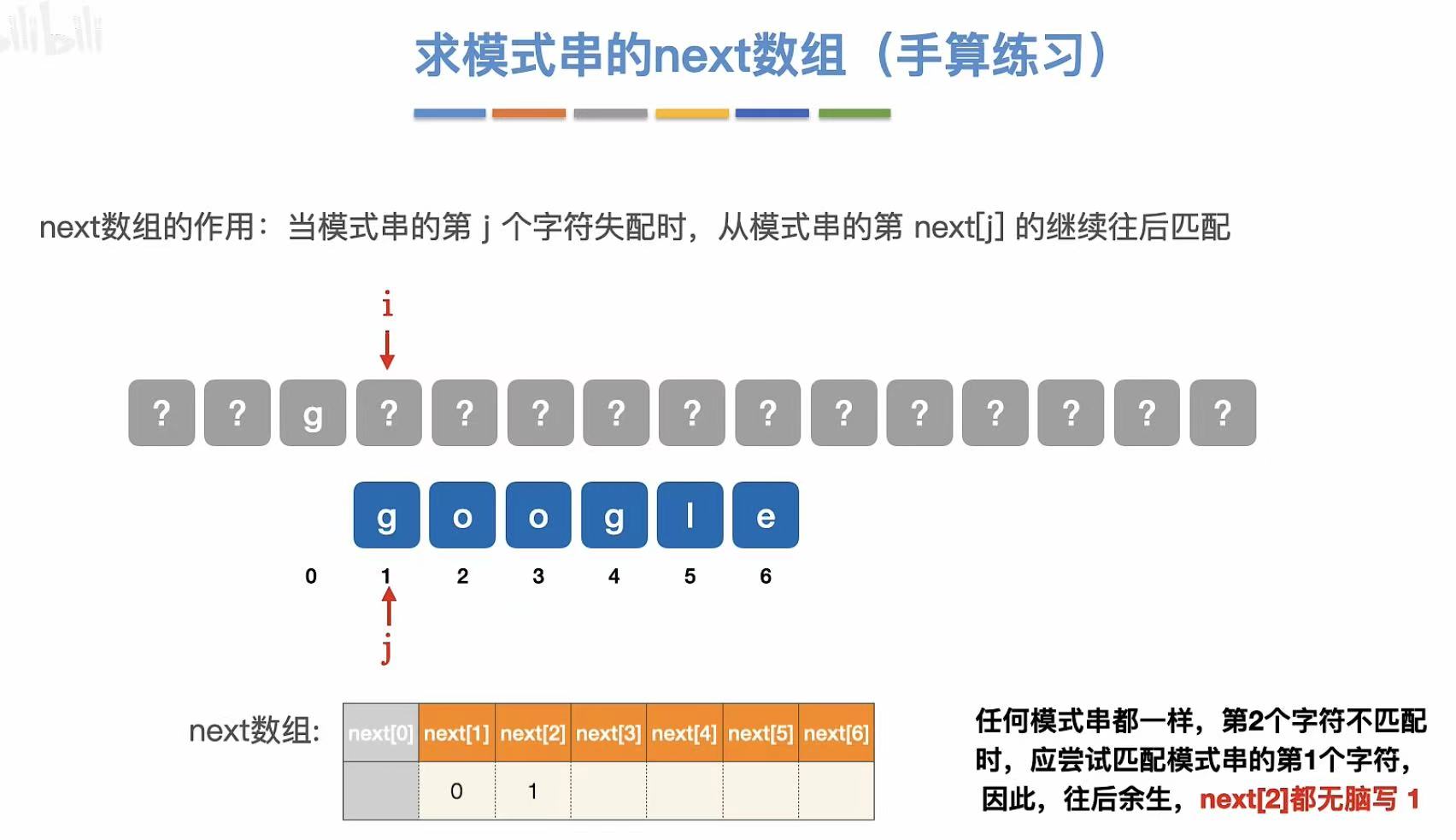
java
//next[4]:
???go???
google
?与o不匹配,分隔向后退
//过程:
???go|???
google
o与g不匹配,继续向后退
???go|???
google
所以j还是指向了1(即google的第一个g)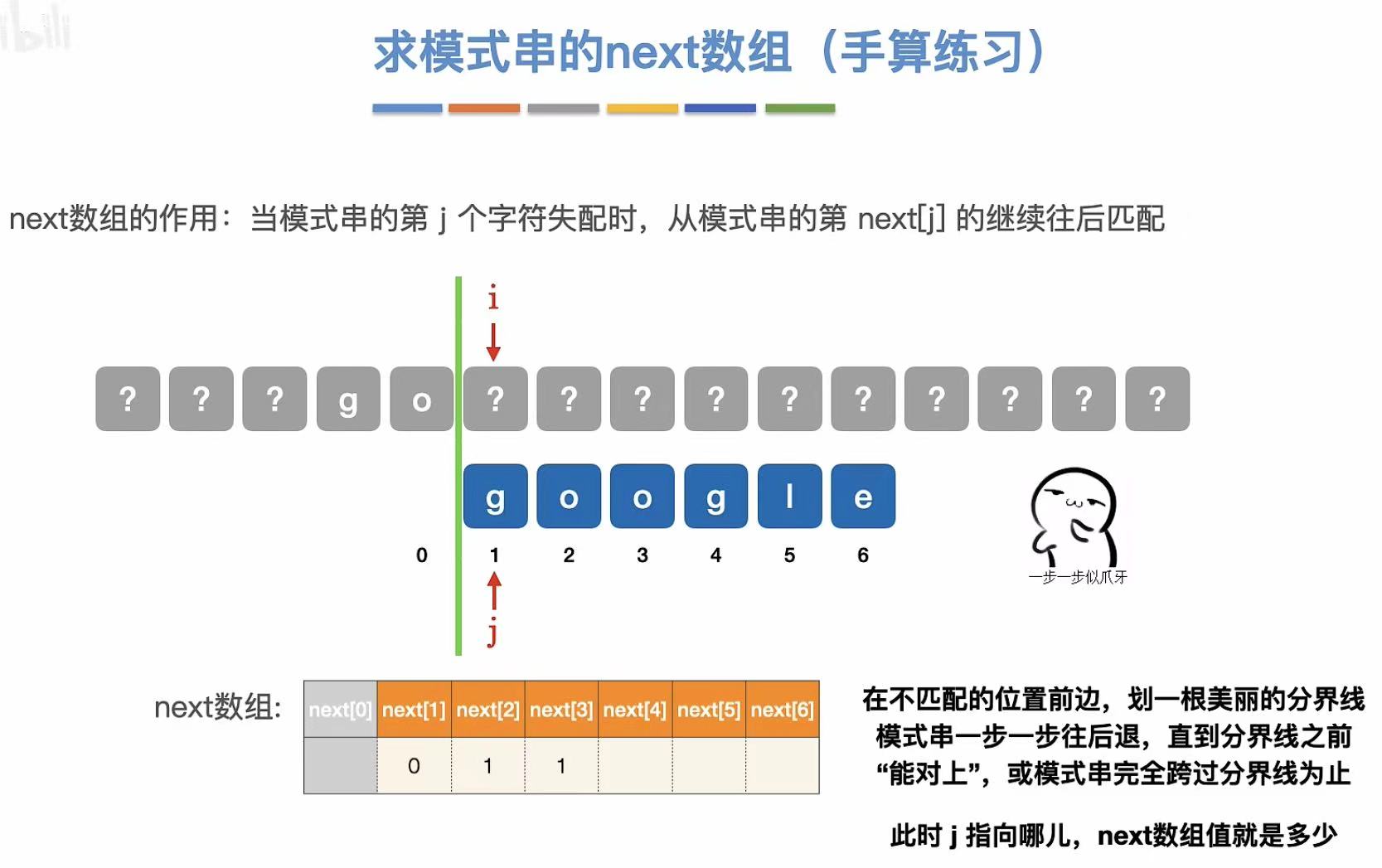
java
//next[4]:
???goo???
google
?与g不匹配,所以分隔向后退
//过程:
???goo|???
google
o与g不匹配,继续向后退
???goo|???
google
o与g不匹配,继续向后退
???goo|???
google
所以j还是指向了1(即google的第一个g)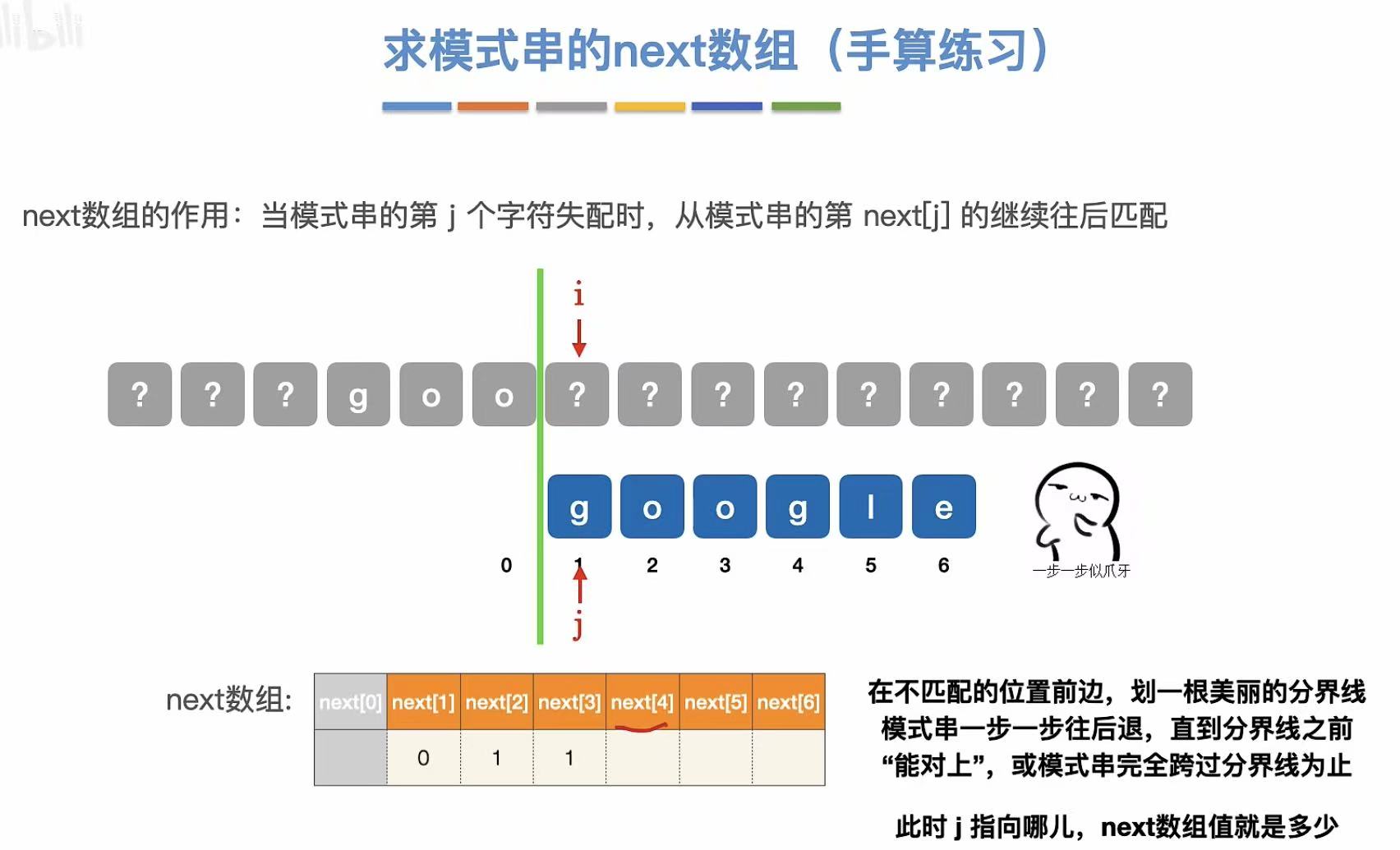
java
//next[5]:
?goog??
google
?与l不匹配,所以分隔向后退
//过程:
?goog|???
google
o与g不匹配,继续向后退
?goog|???
google
o与g不匹配,继续向后退
?goog|???
google
g与g匹配,所以j指向2(即google的第一个o)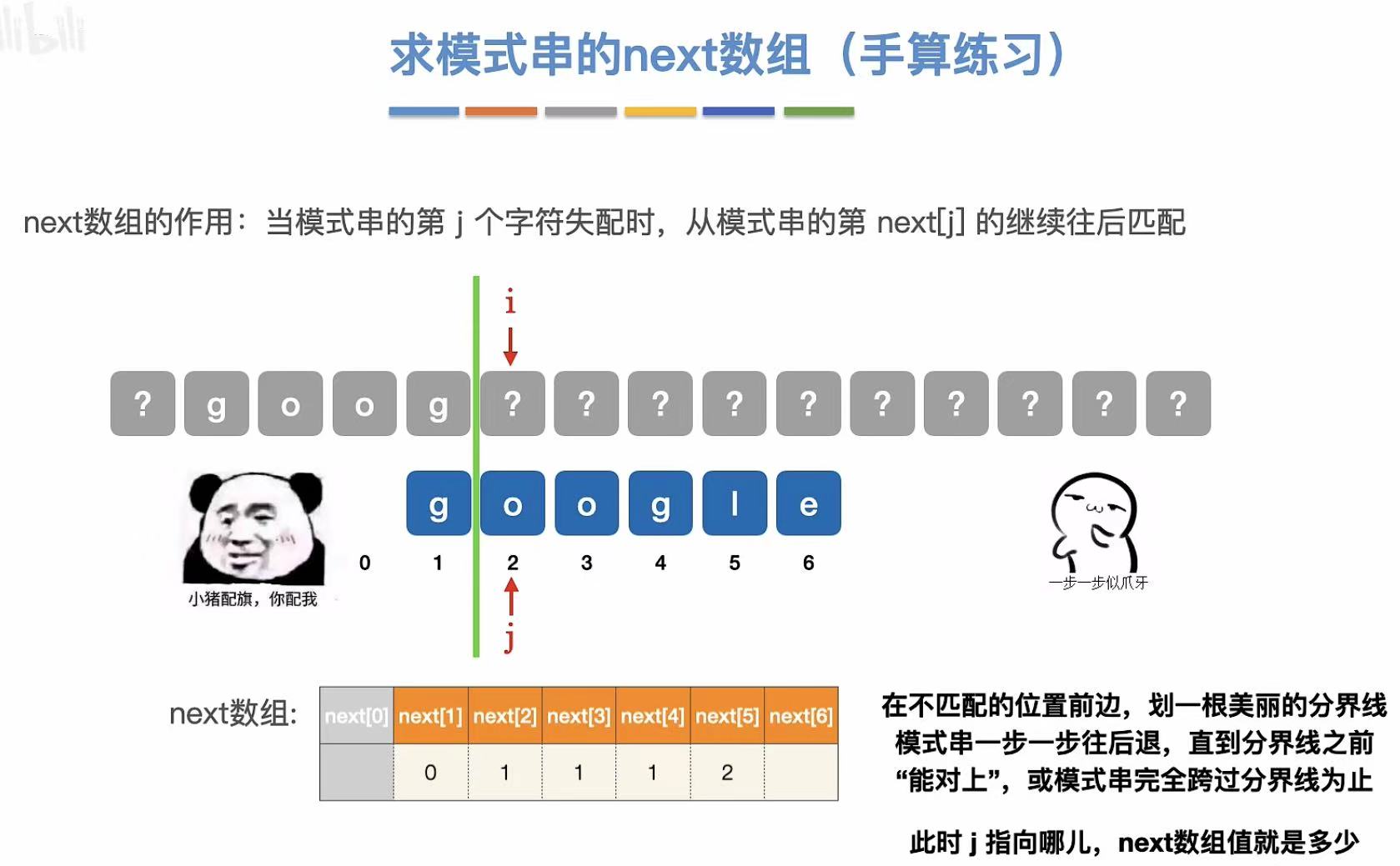
java
//next[6]:
?googl??
google
?与e不匹配,所以分隔向后退
//过程:
?googl|??
google
o与g不匹配,所以分隔向后退
?googl|???
google
o与g不匹配,继续向后退
?googl|???
google
g与g匹配,但l与o不匹配,继续向后退
?googl|???
google
l与g不匹配,继续向后退
?googl|???
google
所以j又重新指向1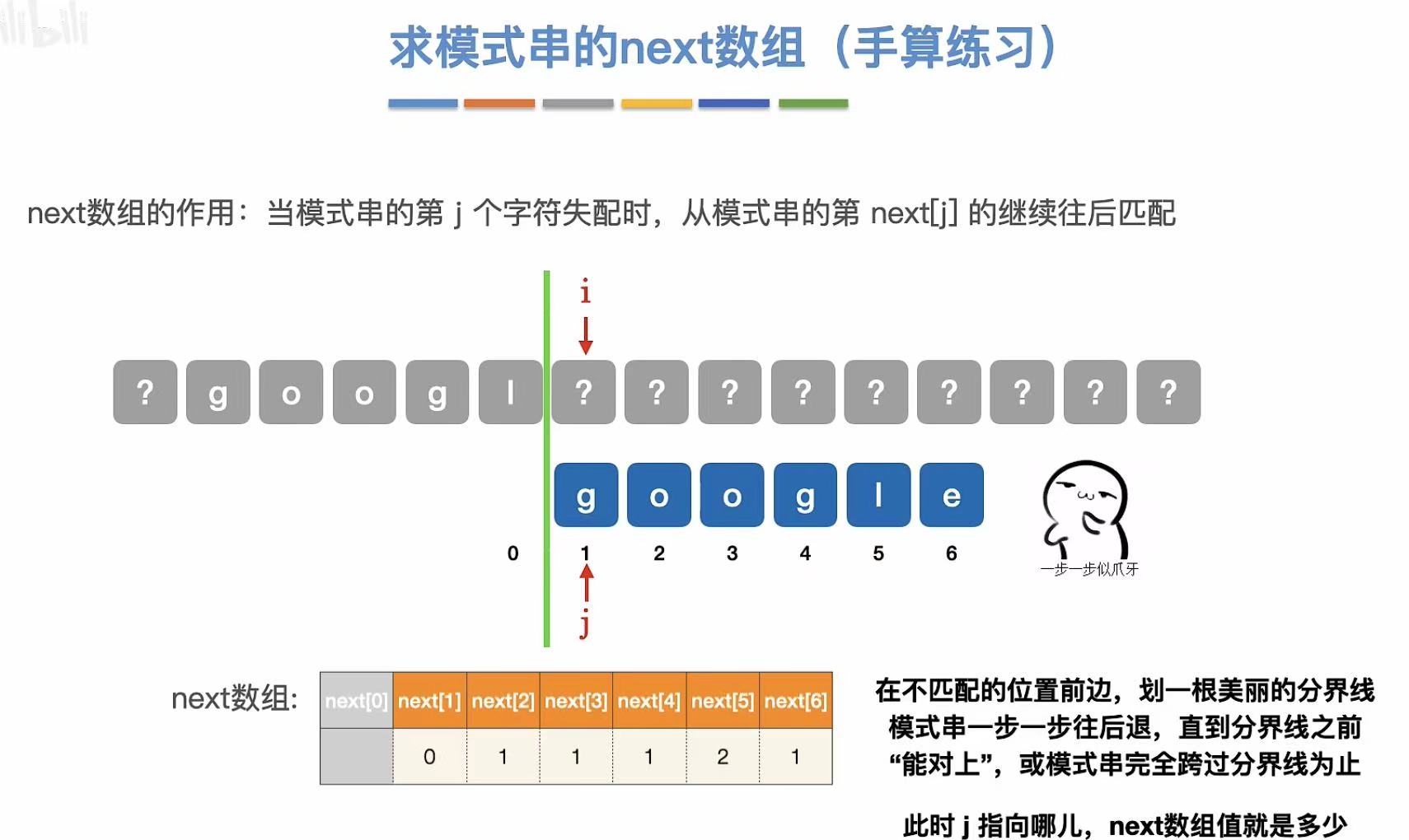
2. 练习2

3. 练习3

4. 小结
KMP的优化
如果第五个元素不匹配,模式串的第五个元素是b,所以主串的第五个元素就肯定不是b。
因为匹配串的a可以与主串的第四个元素重合,但是匹配串的第二个元素是b,主串的第五个元素不能是b,所以就可以越过这个选择。
直接让j指向1,所以就可以优化原来next数组中的next[5],让它的数值变为1.
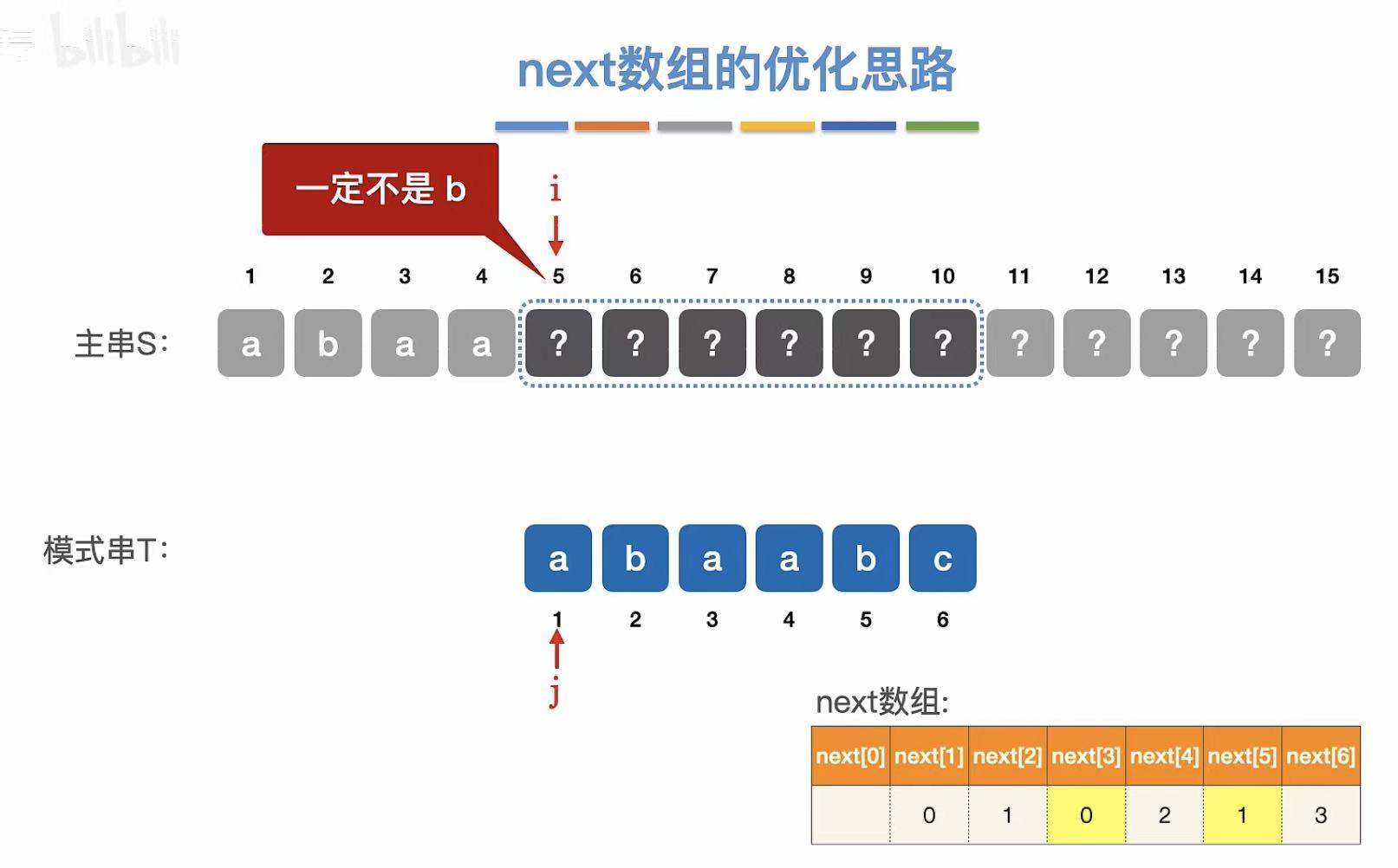
优化后的数组就是nextval数组。
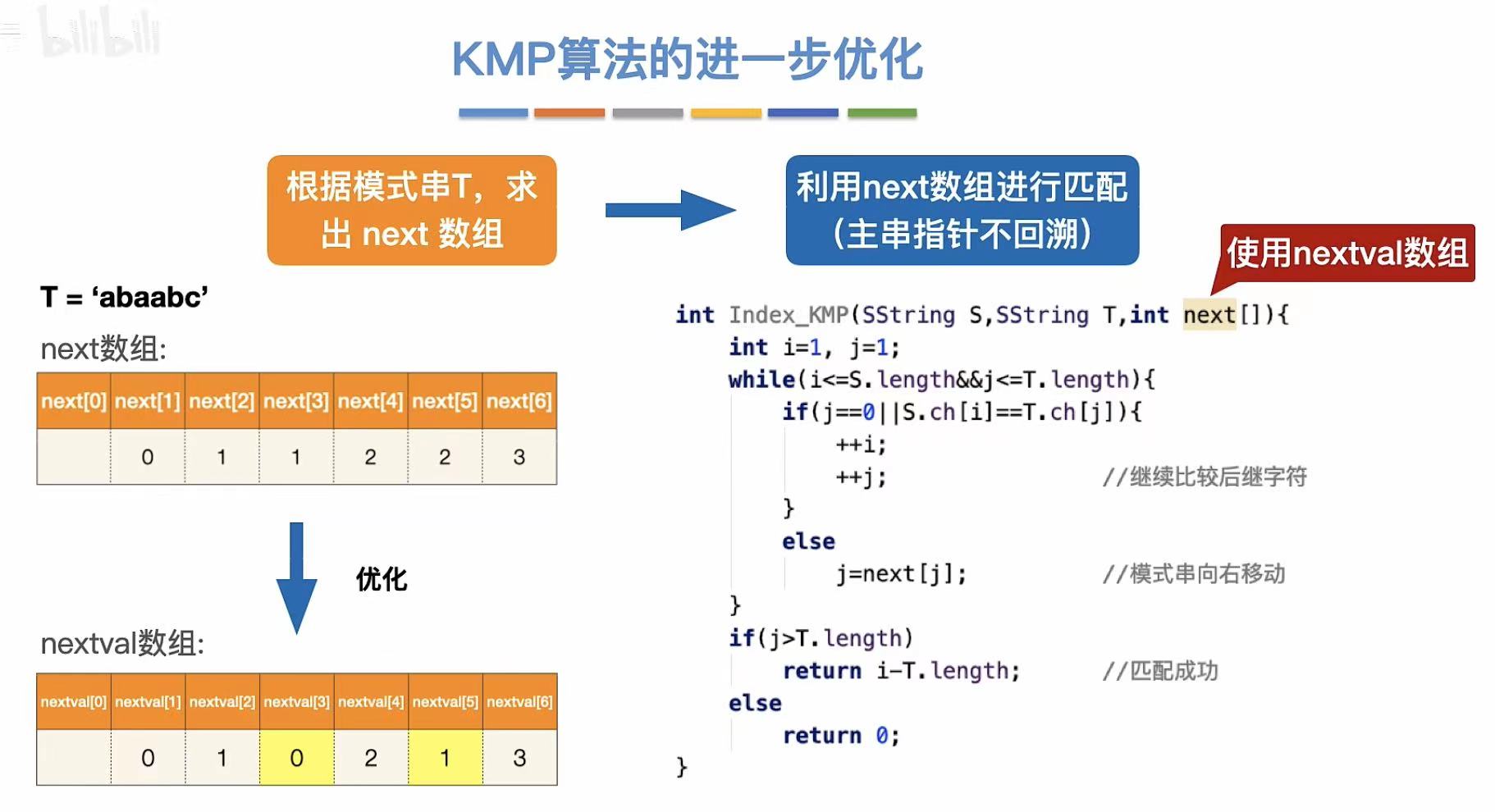
求nextval数组的步骤:
- 先求 next 数组(基于最长公共前后缀)
- 再求 nextval 数组,规则为:
若 T[j] == T[next[j]] → nextval[j] = nextval[next[j]]
否则 → nextval[j] = next[j]

