【最后203篇系列】036 MDP学习思考

0 原则

不做数学公式推导，只是理解概念，然后用程序说明。

1 MDP是什么？

MDP 是对环境的建模假设与形式化描述，本身不参与优化；

优化发生在给定 MDP 假设下，对策略或价值的求解过程。

MDP的 (S, A, P, R, γ) 五元组，描述了一个决策环境：

S, A, P, R 描述了环境的规则：在什么状态 s 下，采取动作 a 后，会以多大概率 P 转移到什么新状态 s'，并得到多少即时奖励 R。

γ 是一个偏好参数，决定了我们如何看待未来奖励（折现因子）。

MDP本身没有可优化的变量，它是一个给定的、对世界的描述。

为什么重要？

在 model-free RL 中：

我们甚至不知道完整的 𝑃,𝑅但仍然假设环境满足 MDP 性质

在 model-based RL 中：

我们会去近似或学习 𝑃,𝑅但目标仍然是策略

2 MDP关注什么？

2.1 策略

当我们"解决"一个MDP问题时，我们是在寻找一个策略 π。

策略 π 是智能体的"大脑"，是一个从状态 s 到动作 a 的映射。它告诉智能体在某个状态下应该做什么。

π 有两种形式：

确定性策略：a = π(s)，直接输出一个动作。

随机性策略：π(a|s)，输出在状态 s 下采取每个动作 a 的概率分布。

π 是我们唯一可以设计和控制的部分，因此它是直接的优化对象。我们通过调整 π 的参数（例如神经网络的权重）来改变智能体的行为。

策略 π 本质上定义了一个"闭环系统" 环境不再随机游走，而是被 π 驱动

2.2 终极目标-回报

概念：

累计回报（return），折现后的长期结

即时奖励（reward），单次行动的回报

虽然我们调整的是 π，但我们判断 π 好坏的标准是它带来的长期回报。这通常通过两个核心的价值函数来度量：

2.2.1 状态价值函数

"从当前状态s出发，按照策略π行动，未来能获得的总奖励的期望值。"

状态价值函数 V^π(s)：在状态 s 开始，一直遵循策略 π 所获得的期望累计回报。

可以更通俗地理解为：

站在状态s这个位置上
按照你现在的决策方式π来玩游戏
你预期未来总共能得多少分

2.2.2 动作价值函数

状态-动作价值函数 Q^π(s, a)：在状态 s 下采取动作 a，然后之后遵循策略 π 所获得的期望累计回报。

"在s状态下，试试动作a看看，评估它到底有多好。"

"在状态s时，如果我强行先做动作a，然后再老老实实按策略π行事，这样一整趟下来我能得到多少总奖励。"

2.2.3 总结

我们的终极优化目标可以写为：

想象你在一个十字路口（状态s）。

V^π(s) （状态价值函数）

问题："按照我平时的习惯（策略π）开车，从这个路口开始，我到家能有多顺利（预期总奖励）？"

答案：这直接反映了你当前策略在这个位置的整体好坏。

决策：它已经隐含了你会按照π选择动作（比如π规定这里应该直行）。

Q^π(s, a) （状态-动作价值函数）

问题："如果在这个路口，我不管平时的习惯，而是特地选择左转/右转/直行（动作a），然后再按习惯开回家，这样做的总效果会怎样？"

答案：这评估了在状态s下，每一个具体动作a的独立价值。

决策：它让你能比较不同动作的好坏。

存在一个最优策略 π*，

对应的状态价值函数和动作价值函数分别记为

V*(s) = V^{π*}(s)

Q*(s, a) = Q^{π*}(s, a)

V 是"我按习惯活下去会怎样"，
Q 是"如果我现在破一次例会怎样"。

3 示例

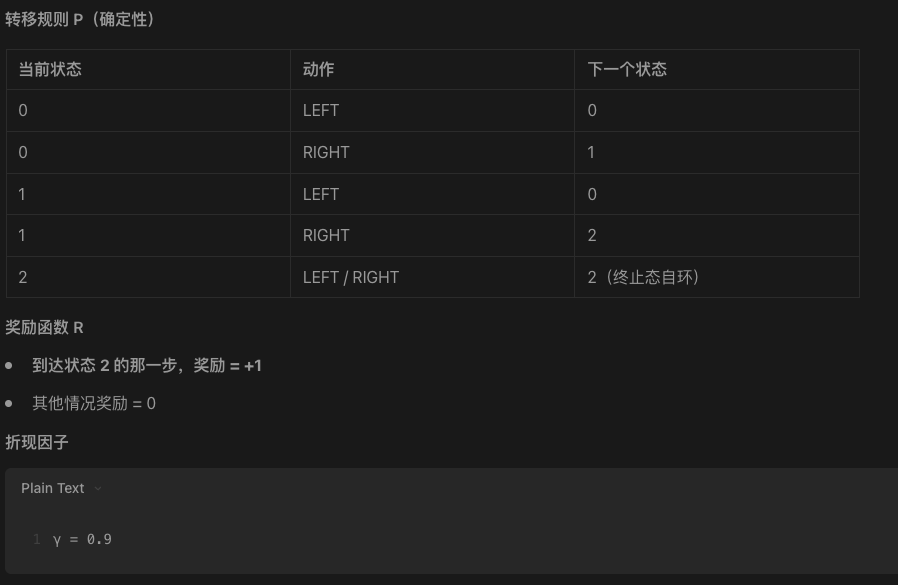
我找了一个例子，比较能帮助理解。这个对应了一维世界的情况，一个点只能左右移动，只要到2就是终点。

3.1 环境

状态空间 S

S = {0, 1, 2}

0：最左边

1：中间

2：终点（terminal）

动作空间 A

A = {LEFT, RIGHT}

假设我们有两个策略：

策略一：π₁（随机乱走）

在非终止状态下，左右各 50%

bash 复制代码

pi_random = {
    0: {"LEFT": 0.5, "RIGHT": 0.5},
    1: {"LEFT": 0.5, "RIGHT": 0.5},
    2: {"LEFT": 0.0, "RIGHT": 0.0},  # terminal
}

策略二：π₂（明确向右）

在 0、1 状态下总是 RIGHT

bash 复制代码

pi_right = {
    0: {"LEFT": 0.0, "RIGHT": 1.0},
    1: {"LEFT": 0.0, "RIGHT": 1.0},
    2: {"LEFT": 0.0, "RIGHT": 0.0},
}

所以问题是，我们怎么知道那种策略更好，或者说面对一个未知问题时，那种策略最好？

4 代码解析

以下快速的过一些代码

定义主要参数。两个函数，step函数是强化学习里常见的，每回合处于某个状态下，采取某个行动，然后会返回一个新状态和奖励。另一个则是策略的评估函数：当策略固定，那么多次迭代后就会趋近收敛。（马尔科夫性，贝尔曼算子压缩性）

python 复制代码

# 假设存在两种策略，用于比较
pi_random = {
    0: {"LEFT": 0.5, "RIGHT": 0.5},
    1: {"LEFT": 0.5, "RIGHT": 0.5},
    2: {"LEFT": 0.0, "RIGHT": 0.0},  # terminal
}

pi_right = {
    0: {"LEFT": 0.0, "RIGHT": 1.0},
    1: {"LEFT": 0.0, "RIGHT": 1.0},
    2: {"LEFT": 0.0, "RIGHT": 0.0},
}

# 下面是mdp描述的世界
states = [0, 1, 2]
actions = ["LEFT", "RIGHT"]
gamma = 0.9

def step(state, action):
    if state == 2:
        return 2, 0

    if state == 0:
        next_state = 0 if action == "LEFT" else 1
    elif state == 1:
        next_state = 0 if action == "LEFT" else 2

    reward = 1 if next_state == 2 else 0
    return next_state, reward

# 评估，多次动作获得收敛的结果
def policy_evaluation(pi, iterations=20, verbose = False):
    V = {s: 0.0 for s in states}

    for _ in range(iterations):
        if verbose:
            print('V',V)
        new_V = {}
        for s in states:
            if s == 2:
                new_V[s] = 0.0
                continue

            v = 0.0
            for a, prob in pi[s].items():
                next_s, r = step(s, a)
                v += prob * (r + gamma * V[next_s])
            new_V[s] = v

        V = new_V

    return V

因此，我们可以评估在两种不同策略下，状态的价值

python 复制代码

# 运行：固定 π → V 收敛
V_random = policy_evaluation(pi_random, verbose=True)
V_right = policy_evaluation(pi_right, verbose= True )

print("V under random policy:", V_random)

V {0: 0.0, 1: 0.0, 2: 0.0}
V {0: 0.0, 1: 0.5, 2: 0.0}
V {0: 0.225, 1: 0.5, 2: 0.0}
V {0: 0.32625000000000004, 1: 0.6012500000000001, 2: 0.0}
V {0: 0.41737500000000005, 1: 0.6468125, 2: 0.0}
V {0: 0.47888437500000003, 1: 0.68781875, 2: 0.0}
V {0: 0.52501640625, 1: 0.71549796875, 2: 0.0}
V {0: 0.5582314687500001, 1: 0.7362573828125, 2: 0.0}
V {0: 0.582519983203125, 1: 0.7512041609375, 2: 0.0}
V {0: 0.6001758648632813, 1: 0.7621339924414063, 2: 0.0}
V {0: 0.6130394357871094, 1: 0.7700791391884766, 2: 0.0}
V {0: 0.6224033587390136, 1: 0.7758677461041992, 2: 0.0}
V {0: 0.6292219971794458, 1: 0.7800815114325561, 2: 0.0}
V {0: 0.6341865788754009, 1: 0.7831498987307506, 2: 0.0}
V {0: 0.6378014149227682, 1: 0.7853839604939303, 2: 0.0}
V {0: 0.6404334189375143, 1: 0.7870106367152456, 2: 0.0}
V {0: 0.642349825043742, 1: 0.7881950385218814, 2: 0.0}
V {0: 0.6437451886045306, 1: 0.7890574212696839, 2: 0.0}
V {0: 0.6447611744433965, 1: 0.7896853348720387, 2: 0.0}
V {0: 0.6455009291919458, 1: 0.7901425284995285, 2: 0.0}
V under random policy: {0: 0.6460395559611635, 1: 0.7904754181363756, 2: 0.0}

print("V under right policy:", V_right)
V {0: 0.0, 1: 0.0, 2: 0.0}
V {0: 0.0, 1: 1.0, 2: 0.0}
V {0: 0.9, 1: 1.0, 2: 0.0}
V {0: 0.9, 1: 1.0, 2: 0.0}
V {0: 0.9, 1: 1.0, 2: 0.0}
V {0: 0.9, 1: 1.0, 2: 0.0}
V {0: 0.9, 1: 1.0, 2: 0.0}
V {0: 0.9, 1: 1.0, 2: 0.0}
V {0: 0.9, 1: 1.0, 2: 0.0}
V {0: 0.9, 1: 1.0, 2: 0.0}
V {0: 0.9, 1: 1.0, 2: 0.0}
V {0: 0.9, 1: 1.0, 2: 0.0}
V {0: 0.9, 1: 1.0, 2: 0.0}
V {0: 0.9, 1: 1.0, 2: 0.0}
V {0: 0.9, 1: 1.0, 2: 0.0}
V {0: 0.9, 1: 1.0, 2: 0.0}
V {0: 0.9, 1: 1.0, 2: 0.0}
V {0: 0.9, 1: 1.0, 2: 0.0}
V {0: 0.9, 1: 1.0, 2: 0.0}
V {0: 0.9, 1: 1.0, 2: 0.0}

V under right policy: {0: 0.9, 1: 1.0, 2: 0.0}

可以看到随机策略在每一个状态下的V(value)都弱于来自上帝视角的确定性策略。

接下来回顾之前的概念：

V(s): 状态价值函数

表示在状态s下，按照当前策略能获得的期望回报

例， V_random[0] = 0.646 # 在状态0下，随机策略的期望回报

Q(s, a): 动作价值函数

表示在状态s下，先执行动作a，然后按照当前策略能获得的期望回报

例，Q_random[0]['RIGHT'] # 在状态0下，先向右走，然后按随机策略的期望回报

V 是"我按习惯活下去会怎样"，
Q 是"如果我现在破一次例会怎样"。

bash 复制代码

对于每个状态s和动作a：
next_s, r = step(s, a)           # 获得下一个状态和即时奖励
Q[s][a] = r + gamma * V[next_s]  # Q = 即时奖励 + 折扣后的下一状态价值

python 复制代码

def compute_Q_from_V(V):
    Q = {}
    for s in states:
        Q[s] = {}
        for a in actions:
            next_s, r = step(s, a)
            Q[s][a] = r + gamma * V[next_s]
    return Q

Q_random = compute_Q_from_V(V_random)
Q_right = compute_Q_from_V(V_right)

print("Q under random policy:", Q_random)
print("Q under right policy:", Q_right)

Q under random policy: {0: {'LEFT': 0.5814356003650472, 'RIGHT': 0.7114278763227381}, 1: {'LEFT': 0.5814356003650472, 'RIGHT': 1.0}, 2: {'LEFT': 0.0, 'RIGHT': 0.0}}
Q under right policy: {0: {'LEFT': 0.81, 'RIGHT': 0.9}, 1: {'LEFT': 0.81, 'RIGHT': 1.0}, 2: {'LEFT': 0.0, 'RIGHT': 0.0}}

使用贪心方法从Q函数生成新策略：对每个状态遍历，如果是终端状态，则所有动作概率设为0；否则，从Q函数中选择该状态下Q值最大的动作，将其概率设为1，其他动作概率设为0

bash 复制代码

开始
↓
对于每个状态s：
│
├─ 如果s是终端状态：
│   ├─ 对于每个动作a：
│   │   └─ 设置π(s,a) = 0.0
│   └─ 继续下一个状态
│
├─ 否则（s非终端）：
│   ├─ 找到max_a Q(s,a)
│   │   （可能有多个动作具有相同的最大Q值）
│   │
│   ├─ 对于每个动作a：
│   │   ├─ 如果a是最大Q值动作之一：
│   │   │   └─ 设置π(s,a) = 1.0/k  # k是最大Q值动作数量
│   │   └─ 否则：
│   │       └─ 设置π(s,a) = 0.0
│   └─ 继续下一个状态
│
└─ 返回新策略π

python 复制代码

def greedy_policy_from_Q(Q):
    pi_new = {}

    for s in states:
        pi_new[s] = {}
        if s == 2:
            pi_new[s]["LEFT"] = 0.0
            pi_new[s]["RIGHT"] = 0.0
            continue

        best_action = max(Q[s], key=Q[s].get)
        for a in actions:
            pi_new[s][a] = 1.0 if a == best_action else 0.0

    return pi_new


# 从随机策略开始
pi = pi_random

for i in range(3):
    print(f"\n=== Iteration {i} ===")

    V = policy_evaluation(pi)
    Q = compute_Q_from_V(V)

    print("V:", V)
    print("Q:", Q)

    pi = greedy_policy_from_Q(Q)
    print("New policy:", pi)

=== Iteration 0 ===
V: {0: 0.6460395559611635, 1: 0.7904754181363756, 2: 0.0}
Q: {0: {'LEFT': 0.5814356003650472, 'RIGHT': 0.7114278763227381}, 1: {'LEFT': 0.5814356003650472, 'RIGHT': 1.0}, 2: {'LEFT': 0.0, 'RIGHT': 0.0}}
New policy: {0: {'LEFT': 0.0, 'RIGHT': 1.0}, 1: {'LEFT': 0.0, 'RIGHT': 1.0}, 2: {'LEFT': 0.0, 'RIGHT': 0.0}}

=== Iteration 1 ===
V: {0: 0.9, 1: 1.0, 2: 0.0}
Q: {0: {'LEFT': 0.81, 'RIGHT': 0.9}, 1: {'LEFT': 0.81, 'RIGHT': 1.0}, 2: {'LEFT': 0.0, 'RIGHT': 0.0}}
New policy: {0: {'LEFT': 0.0, 'RIGHT': 1.0}, 1: {'LEFT': 0.0, 'RIGHT': 1.0}, 2: {'LEFT': 0.0, 'RIGHT': 0.0}}

=== Iteration 2 ===
V: {0: 0.9, 1: 1.0, 2: 0.0}
Q: {0: {'LEFT': 0.81, 'RIGHT': 0.9}, 1: {'LEFT': 0.81, 'RIGHT': 1.0}, 2: {'LEFT': 0.0, 'RIGHT': 0.0}}
New policy: {0: {'LEFT': 0.0, 'RIGHT': 1.0}, 1: {'LEFT': 0.0, 'RIGHT': 1.0}, 2: {'LEFT': 0.0, 'RIGHT': 0.0}}

可以看到，最忌策略下的V计算出来后估算Q，然后再用贪婪方法优化策略，然后再将策略固定，再计算V... 反复迭代后可以看到V和Q都是稳定的。

以上就是对于策略的迭代：

1 策略迭代算法有效：能从随机策略收敛到最优策略
2 收敛性保证：算法会在有限次迭代内收敛
3 策略改进定理实用：每次迭代确实改进策略
4 Q函数的重要性：连接V函数和策略改进的桥梁

这部分就到这里，除了策略迭代，还有值迭代，这部分会和qlearning 更紧密，下次接着写。