本系列文章详细介绍Transformer架构,请参考往期文章:
一、Encoder总体结构解析
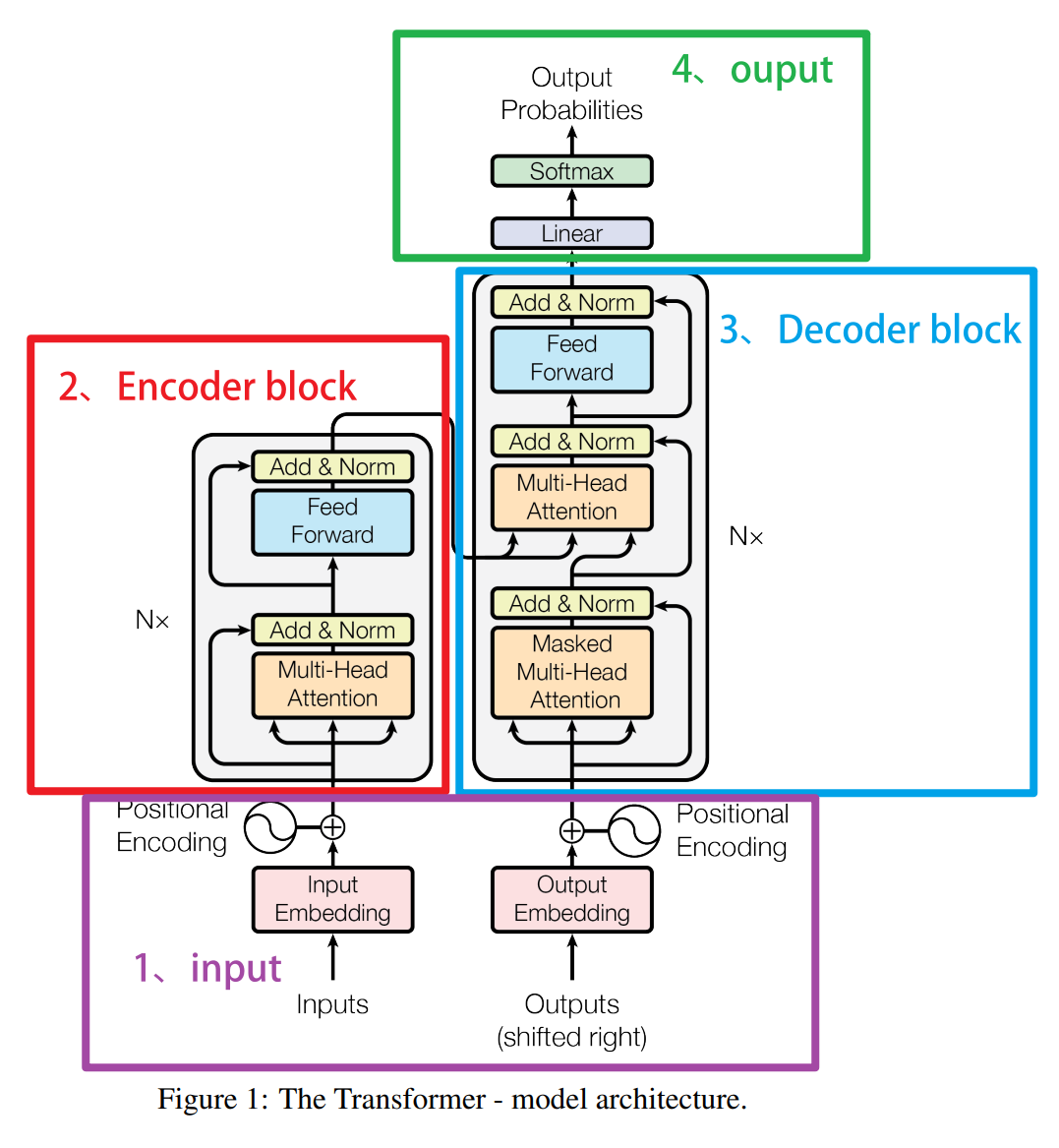
编码器(Encoder)结构包括两个子层:一个是自注意力(Self-Attention)层,另一个是前馈(Feed-Forward)神经网络。输入会先经过自注意力层,这层的作用是帮助模型关注输入序列中不同位置的信息。然后,经过前馈神经网络层,这是一个简单的全连接神经网络。两个子层都有一个残差连接(Residual Connection)和层标准化(Layer Normalization)。
二、残差连接
观察Transformer 的结构不难发现------在多头注意力机制之后,我们输出的信息(通常用 z 1 z_1 z1表示)并没有直接传入前馈神经网络,而是经过了一个Add & Normalize层,这是什么操作,代表了什么含义呢?
首先来看Add ,这里的Add表示"加和",是在多头注意力机制输出的信息的基础上加了一个输入数据y自身,这个数据y是从输入层传过来的。这种通过两条链路并行、一条链路进行复杂计算(在这里是多头注意力机制)、一条链路将输入数据y原封不动传到架构后方、并且最终让两条链路上的输出结果进行加和的操作,叫做残差操作。与复杂链路并行、负责将y进行传输的链路就是残差链接。
在之前的课程里我们详细地讲解过残差网络,残差网络正是利用残差链接来对抗深度神经网络的"退化问题"。何凯明在2015年提出的残差网络(ResNet)https://aryiv.org/abs/1512.03385 中提出了残差链接的构想,这是他当时构想的最基础的残差块的设计,如你所见,也是让残差链接与复杂链路并行的结构。
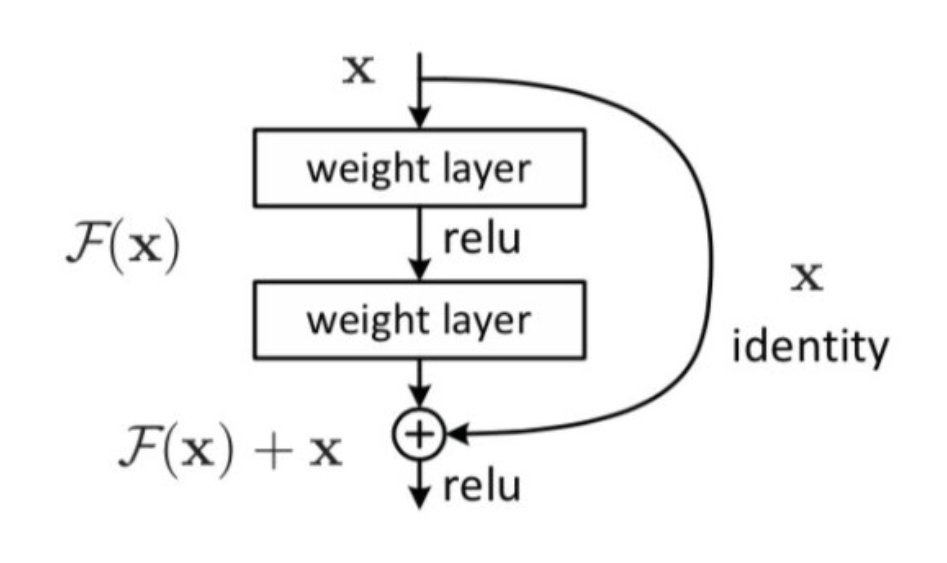
这种将y原封不动传到架构后方的操作可以解决梯度消失问题、可以让模型学到恒等映射(输入与输出相等)、可以让训练被简化、加速训练收敛、同时非常重要的是,还能避免网络在加深的时候出现退化问题。在之前讲解残差网络的时候,我们深读了残差网络的原始论文,详细解读了为什么残差链接让网络拟合恒等函数却能够获得很好的效果,讲解了这个反直觉的架构设计是如何逼迫网络变得越来越强。在Transformer中,残差链接可以说承担着各种方面的职责,从实验的结果来看,在各层次上加上残差链接可以让Transformer效果更好。
在残差链接的所有效果中,我们可以从数学角度、非严格证明一下它为什么能够解决梯度消失问题。
假设现在存在一个神经网络,它由多个残差结构相连(就像transformer一样) 。每个残差结构被定义为F(x,W),这个结构是由一个复杂结构 + 一个残差链接并行而成的,其中 x x x代表残差输入的数据, W W W代表该结构中的权重。设 x i , x i + 1 x_i, x_{i+1} xi,xi+1分别代表残差结构F()的输入和输出,设 x I x_I xI代表整个神经网络的输入,令relu激活函数为 r ( y ) = m a x ( 0 , x ) r(y)=max(0,x) r(y)=max(0,x),简写为 r ( ) r() r()。由此可得:
x i + 1 = r ( x i + F ( x i , W i ) ) x i + 2 = r ( x i + 1 + F ( x i + 1 , W i + 1 ) ) ... ... 如果relu激活函数是被激活状态(残差结构输出的值都大于0),则有 x i + 1 = x i + F ( x i , W i ) x i + 2 = x i + 1 + F ( x i + 1 , W i + 1 ) ... ... 这是一个递归嵌套结构,如此递归推导可以得到 x I = x i + ∑ n = i I − 1 F ( x n , W n ) \begin{aligned} x_{i+1} & = r(x_i + F(x_i, W_i)) \\ x_{i+2} & =r(x_{i+1}+F(x_{i+1},W_{i+1})) \\ ...... \\ &\text{如果relu激活函数是被激活状态(残差结构输出的值都大于0),则有} \\ x_{i+1} & = x_i + F(x_i, W_i) \\ x_{i+2} & =x_{i+1}+F(x_{i+1},W_{i+1}) \\ ...... \\ &\text{这是一个递归嵌套结构,如此递归推导可以得到} \\ x_I & =x_i+\sum_{n=i}^{I-1}F(x_n,W_n) \end{aligned} xi+1xi+2......xi+1xi+2......xI=r(xi+F(xi,Wi))=r(xi+1+F(xi+1,Wi+1))如果relu激活函数是被激活状态(残差结构输出的值都大于0),则有=xi+F(xi,Wi)=xi+1+F(xi+1,Wi+1)这是一个递归嵌套结构,如此递归推导可以得到=xi+n=i∑I−1F(xn,Wn)
此时如果我们对神经网络的结构求梯度,则会有------
∂ L o s s ∂ x i = ∂ L o s s ∂ x I ∗ ∂ x I ∂ x i = ∂ L o s s ∂ x I ∗ ∂ ( x i + ∑ n = i I − 1 F ( x n , W n ) ) ∂ x i = ∂ L o s s ∂ x I ∗ ( 1 + ∑ n = i I − 1 F ( x n , W n ) ∂ x i ) \begin{aligned} \frac{\partial Loss}{\partial x_{i}}&=\frac{\partial Loss}{\partial x_{I}} * \frac{\partial x_{I}}{\partial x_{i}} \\ &=\frac{\partial Loss}{\partial x_{I}} * \frac{\partial(x_i+\sum_{n=i}^{I-1}F(x_n,W_n))}{\partial x_{i}} \\ &=\frac{\partial Loss}{\partial x_{I}}*(1+\frac{\sum_{n=i}^{I-1}F(x_n,W_n)}{\partial x_{i}}) \end{aligned} ∂xi∂Loss=∂xI∂Loss∗∂xi∂xI=∂xI∂Loss∗∂xi∂(xi+∑n=iI−1F(xn,Wn))=∂xI∂Loss∗(1+∂xi∑n=iI−1F(xn,Wn))
从结果可以看出,因为有"1+"这一结构的存在,可以有效避免梯度消失(求解后梯度为0)的情况,这样网络深层处的梯度可以直接传递到网络的浅层、让迭代变得更加稳定。与此同时,残差网络在更新梯度时把一些乘法转变为了加法,同时也提高了计算效率。
基于残差结构的这些优势,Transformer 在注意力机制的外侧添加了残差链接,从而让 encoder 和 decoder 中的梯度传输都变得更加稳定。
三、 Layer Normalization层归一化
在了解了Add之后,我们来看一下Normalize 。在 Transformer 结构中,Layer Normalization(层归一化)是一个至关重要的部分,它是一种特定的归一化技术,它在2016年被提出,用于减少训练深度神经网络时的内部协方差偏移(internal covariate shift)。我们在课程的 Lesson13-15 部分详细讲解过内部协方差偏移的关键知识,感兴趣的小伙伴可以回到可成 lesson13-15 去详细了解。
与Batch Normalization(批归一化)不同,Layer Normalization 不是对一个批次(batch)中的样本进行归一化,而是独立地对每个样本中的所有特征进行归一化(也就是对单一词向量、单一时间点的所有embedding维度进行归一化)。具体来说,对于每个样本,Layer Normalization 会在特定层的所有激活上计算均值和方差,然后用这些统计量来归一化该样本的激活值。Transformer 的Normalize 使用了2016年 Jimmy Lei Ba 等人的的论文Layer Normalization 。
-
为什么要进行Normalize呢?
-
减少内部协方差偏移 :在深度学习模型训练过程中,参数的更新会影响后续层的激活分布,这可能导致训练过程不稳定。
Layer Normalization通过规范化每一层的输出来减轻这种效应,有助于稳定训练过程。 -
加速训练速度:归一化可以使得梯度更稳定,这通常允许更高的学习率,从而加快模型的收敛速度。
-
减少对初始值的依赖 :由于
Layer Normalization使得模型对于输入数据的分布变化更为鲁棒,因此可以减少模型对于参数初始值的敏感性。 -
允许更深层网络的训练 :通过规范化每层的激活,
Layer Normalization可以帮助训练更深的网络结构,而不会那么容易出现梯度消失或爆炸的问题。
为什么使用 Layer Normalization(LN)而不使用Batch Normalization(BN)呢?
BN 和 LN 的差别就在 u i u_i ui和 σ i \sigma_i σi这里,前者在某一个 Batch 内统计某特定神经元节点的输出分布(跨样本),后者在某一次迭代更新中统计同一层内的所有神经元节点的输出分布(同一样本下)。
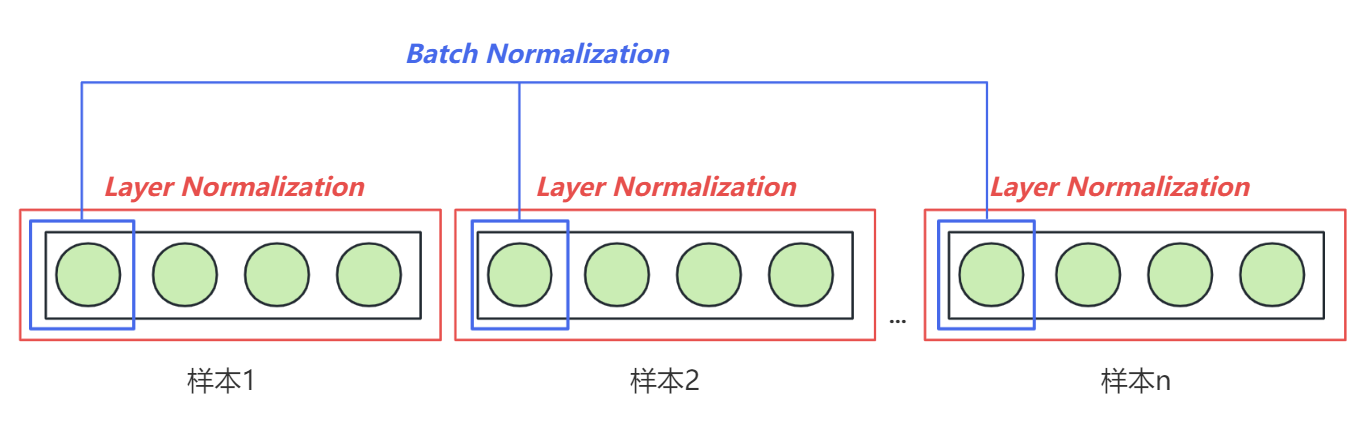
最初BN 是为 CNN 任务提出的,需要较大的 BatchSize 来保证统计量的可靠性,并在训练阶段记录全局的 u u u和 σ \sigma σ供预测任务使用。而LN是独立于batch大小的,它只对单个输入样本的所有特征进行规范化。
NLP任务中经常会处理长度不同的句子,使用LN时可以不考虑其它样本的长度。
在某些情况下,当可用的内存有限或者为了加速训练而使用更小的batch时,BN因为batch数量不足而受到了限制。
在某些NLP任务和解码设置中,模型可能会一个接一个地处理序列中的元素,而不是一次处理整个batch。这样BN就不是很适用了。
在Transformer模型中有很深的层次和自注意机制。通过对每一层的输入进行规范化,可以防止值的爆炸或消失,从而帮助模型更快地收敛。
【扩展】各类Normalization的本质
LN 是 Normalization(规范化)家族中的一员,由 Batch Normalization(BN)发展而来。基本上所有的规范化技术,都可以概括为如下的公式:
h i = f ( a i ) h i ′ = f ( g i σ i ( a i − u i ) + b i ) h_i = f(a_i) \\ \\ {h_i}^{'}=f(\frac{g_i}{\sigma_i}(a_i-u_i)+b_i) hi=f(ai)hi′=f(σigi(ai−ui)+bi)
这个公式描述了Normalization技术中对于单个数据点 a i a_i ai在某一层的激活值进行规范化的过程。这里是每个符号的含义:
- a i a_i ai:原始神经网络层的激活值或输出。
- f f f:应用于规范化之后的值的激活函数。
- h i h_i hi:应用激活函数 f f f 之后的激活值,是规范化步骤之前的输出。
- h i ′ h'_i hi′:最终的规范化输出值。
- σ i \sigma_i σi:用于规范化过程中的尺度调整的标准差。
- u i u_i ui:平均值。
- g i g_i gi:尺度参数。
- b i b_i bi:偏置参数。
对于隐层中某个节点的输出为对激活值 a i a_i ai 进行非线性变换 f ( ) f() f() 后的 h i h_i hi:先使用均值 u i u_i ui和方差 σ i \sigma_i σi对 a i a_i ai 进行分布调整。
- 如果以正态分布为例,就是把"高瘦"(红色)和"矮胖"(蓝紫色)的都调整回正常体型(绿色),把偏离
y=0的(紫色)拉回中间来。
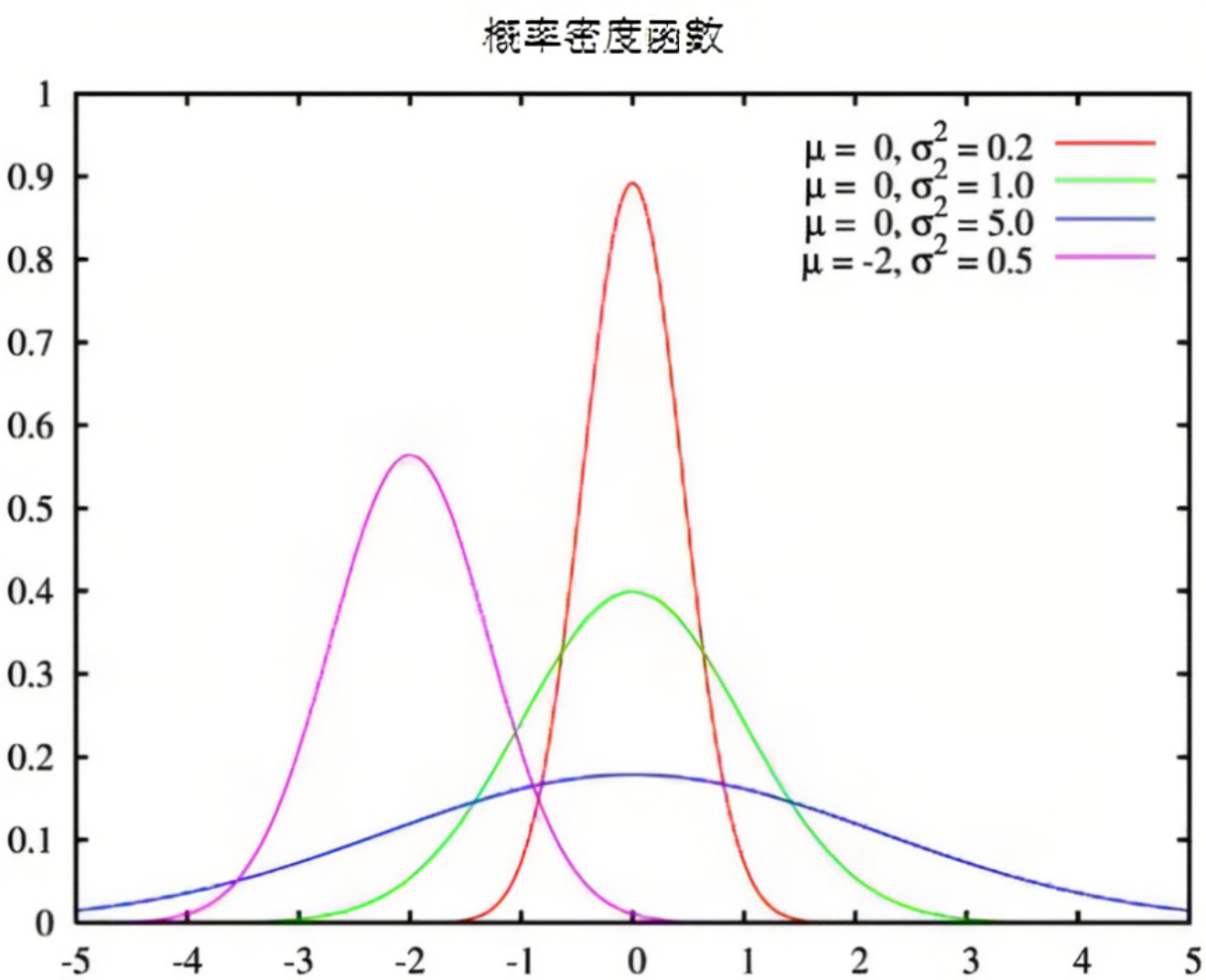
- 这样可以将每一次迭代的数据调整为相同分布,消除极端值,提升训练稳定性。
- 同时"平移"操作,可以让激活值落入 f ( ) f() f()的梯度敏感区间即梯度更新幅度变大,模型训练加快。
然而,在梯度敏感区内,隐层的输出接近于"线性",模型表达能力会大幅度下降。引入 gain 因子 g i g_i gi 和 bias 因子 b i b_i bi,为规范化后的分布再加入一点"个性"。
注: g i g_i gi和 b i b_i bi作为模型参数训练得到 , u i u_i ui和 σ i \sigma_i σi在限定的数据范围内统计得到。
四、Feed-Forward Networks前馈网络
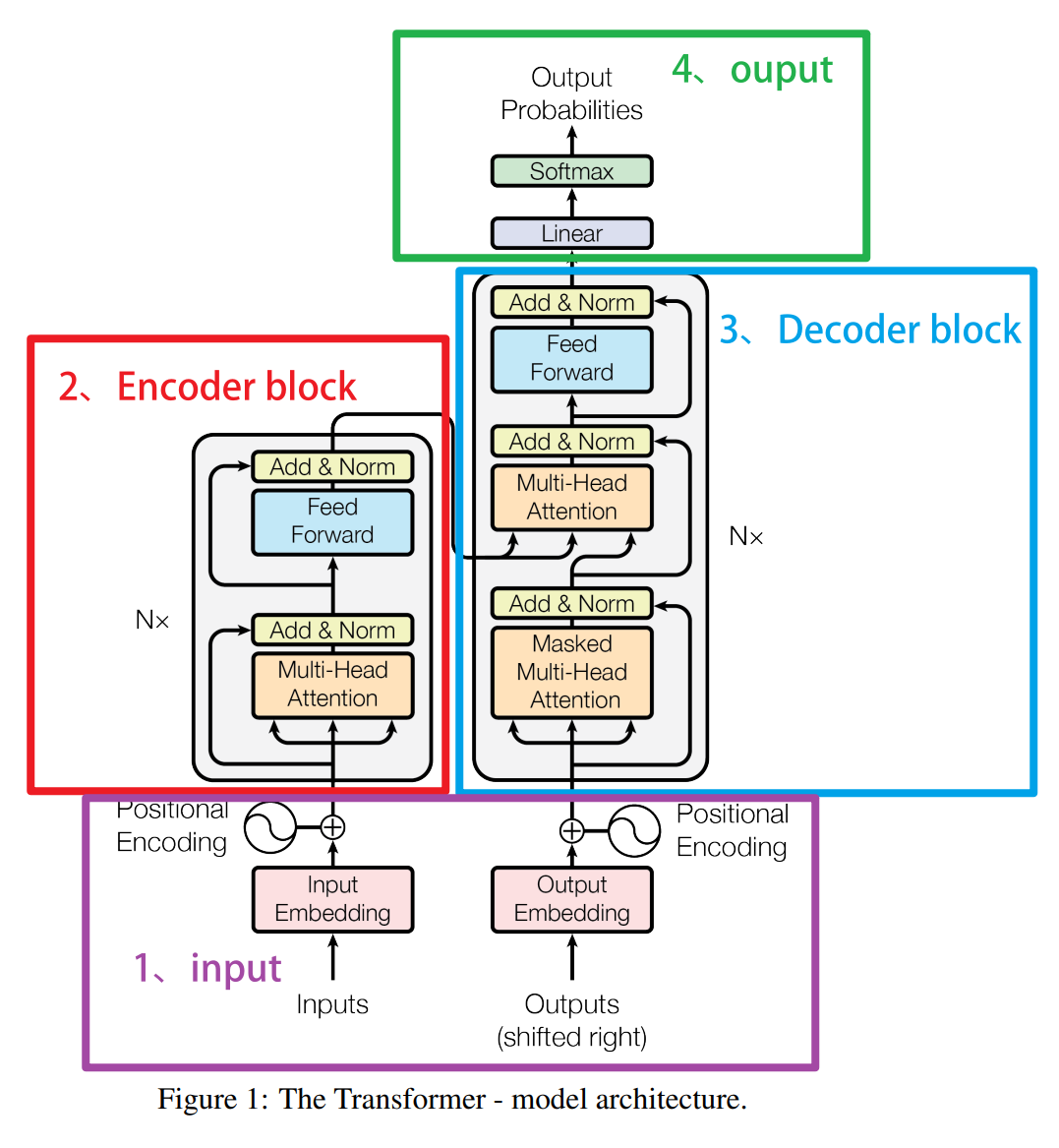
根据Transformer的结构图可以看出,每一个多头注意力机制层都链接了一个前馈网络层。前馈网络(Feed-Forward Networks,FFNs),在神经网络的语境中,是指那些信息单向流动的网络结构。在这样的网络中,信息从输入层流向输出层,中间可能会经过多个隐藏层,但不会有任何反向的信息流,即不存在循环或者回路。因此在 Transformer 当中,实际上前馈神经网络就是由线性层组成的深度神经网络结构 。它的主要职责是对输入数据进行非线性变换,同时也负责产生输出值 。它的作用暗示了一个关键的事实------自注意力机制大多数时候是一个线性结构 :加权求和是一个线性操作,即便我们是经过丰富的权重变化、由丰富的Q、K、V等矩阵点积的结果,还有 softmax 函数,但是自注意力机制依然是一个线性的过程。因此,在加入前馈神经网络之前,transformer 本身不带有传统意义上的非线性结构。
在现代深度学习架构中,特别是在 Transformer 模型中,前馈网络通常指的是一个特定的子层,它由两个线性变换组成,中间夹有一个激活函数,如 ReLU 或者 GELU 。具体结构可以表示为:
-
第一层线性变换 :
z 1 = x W 1 + b 1 z_1 = xW_1 + b_1 z1=xW1+b1
- x x x 是输入向量。
- W 1 W_1 W1 和 b 1 b_1 b1 是第一层的权重矩阵和偏置向量。
-
ReLU激活函数 :
a 1 = ReLU ( z 1 ) = max ( 0 , z 1 ) a_1 = \text{ReLU}(z_1) = \max(0, z_1) a1=ReLU(z1)=max(0,z1)
ReLU的作用是引入非线性,使得网络能够学习更复杂的函数映射。ReLU函数将输入中的负值置为零,正值保持不变。
-
第二层线性变换:
- a 1 a_1 a1 是经过
ReLU激活后的中间表示。 - W 2 W_2 W2 和 b 2 b_2 b2 是第二层的权重矩阵和偏置向量。
- 最终输出 z 2 z_2 z2 是前馈神经网络的输出。
- a 1 a_1 a1 是经过
合起来,前馈神经网络的完整表达式为:
F F N ( x ) = max ( 0 , x W 1 + b 1 ) W 2 + b 2 FFN(x) = \max(0, xW_1 + b_1)W_2 + b_2 FFN(x)=max(0,xW1+b1)W2+b2
Transformer 模型中的前馈网络在自注意力层之后对每个位置的表示独立地应用相同的变换,这样可以进一步提高网络的表示能力。由于在前馈网络中对每个位置进行的是相同的操作,所以它们非常适合于并行计算。这种层通常被设计为宽度很大,以便在模型中捕获大量的特征并提供足够的模型容量。
以线性层作为输出层是许多深度学习架构的经典操作。Encoder在最后使用的前馈神经网络可以说是以线性层结尾,它本身有激活函数,可以产生输出,因此Encoder编码器部分是可以单独使用的结构 。在许多情况下,我们可以单独使用 Encoder 的输出来执行各种任务,而不需要 Decoder 解码器部分,下面是一些经典的场景------
encoder走位特征提取器 :Encoder 的输出可以用作特征提取器,将输入序列转换为一系列有意义的特征表示。这些特征表示可以用于各种机器学习任务,如分类、聚类、序列标注等。
encoder生成类似autoencoder的语义表示 :Encoder 的输出可以被用来获取输入序列的语义表示。这些语义表示可以用于进行语义相似度计算、文本匹配、信息检索等自然语言处理任务。
序列到序列任务的编码器 :在一些序列到序列任务中,只需要对输入序列进行编码,而不需要生成输出序列。例如,文本摘要、问答系统中,只需将输入文本编码为一个语义表示,而无需生成摘要或答案。
预训练模型的基础部分 :许多预训练模型,如BERT(
Bidirectional Encoder Representations from Transformers)等,基于Transformer Encoder架构。在这些模型中,Encoder 的输出可以被用作下游任务的输入,从而提供丰富的语义信息。
具体地来说,有许多任务可以仅使用 Encoder 完成。以下是一些常见的例子:
情感分析 :情感分析任务旨在确定文本的情感倾向,如正面、负面或中性。在这种任务中,我们只需将输入文本编码为一个语义表示,然后通过该表示来预测文本的情感倾向,而不需要生成任何文本输出。
文本分类 :文本分类任务要求将文本分配到预定义的类别中。例如,垃圾邮件过滤、新闻分类等。在这种任务中,我们可以使用 Encoder 将输入文本编码为一个语义表示,然后通过该表示来进行分类预测。
命名实体识别 :命名实体识别任务要求在文本中识别和分类命名实体,如人名、地名、组织名等。在这种任务中,我们可以使用 Encoder 将输入文本编码为一个语义表示,然后通过该表示来对命名实体进行识别。
关系抽取 :关系抽取任务旨在从文本中提取实体之间的关系。例如,在医学文本中,从病历中抽取药物与疾病之间的关系。在这种任务中,我们可以使用 Encoder 将输入文本编码为一个语义表示,然后通过该表示来提取实体之间的关系。
文本生成的预训练:在预训练语言模型中,我们可以使用 Encoder 将输入文本编码为一个语义表示,然后利用这个语义表示来预测下一个词或者生成文本序列。这在自然语言生成任务中非常有用,如对话生成、摘要生成等。
Encoder 在 Transformer 架构中扮演着至关重要的角色,其作用是将输入序列转换为一系列语义表示,以便后续任务的处理和预测。Encoder 的结构包括多个相同的层,每个层都由自注意力机制和前馈神经网络组成,其中自注意力机制用于捕捉输入序列中的全局依赖关系,前馈神经网络用于对每个位置的特征进行非线性变换和提取。Encoder 作为 Transformer 架构的核心组件之一,承担着将输入序列转换为语义表示的重要任务。它的结构设计体现了并行计算、信息流动、层级表示和模块化设计等关键原则,使得模型能够更好地理解和表示输入数据,并在各种文本相关任务中取得优异的性能。