标量投影和向量投影

在上篇文章《欧式内积》中，我们提到过Proj，这篇文章中将深入讨论。

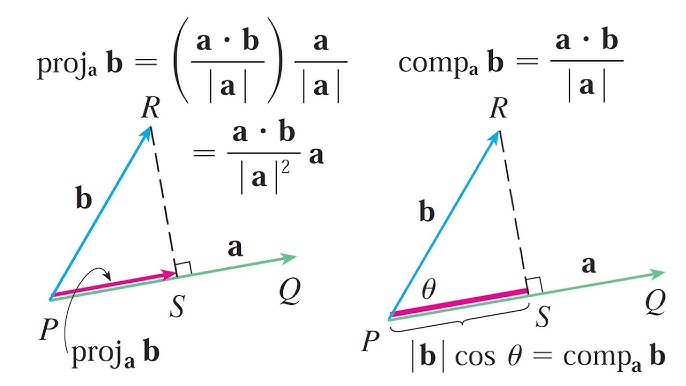
我先把图里的符号（proj、comp、点积、夹角）逐一对应到几何含义，然后用一个带数字的例子把公式算一遍，最后总结两者区别与常见坑。

这张图在讲同一件事的两种"输出"：

把向量 b 在 向量 a 的方向上"投影"
一个输出是向量（projection，写作）
另一个输出是标量长度 （component/ scalar projection，写作）

1) 图里的几何关系：P、Q、R、S 分别是什么

把 P 当作起点（原点）：

绿色箭头 a ：从 P 指向 Q（方向就是 a 的方向）
蓝色箭头 b ：从 P 指向 R
从 R 垂直落到绿色直线（a 的延长线）上的垂足是 S
粉色箭头：这就是 b 在 a 方向上的投影向量

所以：

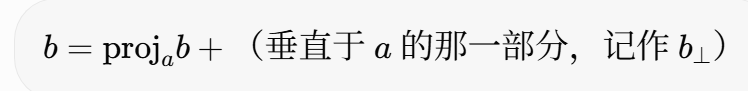
或者：

图中虚线 + 直角符号就是在强调"分解成平行 + 垂直"。

2) 左图：向量投影（结果是一个向量）

图上给了三个等价公式：

怎么理解最直观：

是 a 的单位方向（只保留方向），即单位向量。
是"在这个方向上该走多远"的长度，即标量投影，是坐标值。
所以 长度 × 方向 = 向量投影

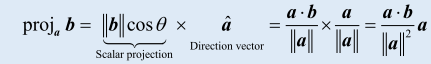
(图片来自《线性代数不难》)

这个投影公式不是死记硬背的公式，而是可以严格推导出来的 。它有多种等价的推导方式，最常见的有两种：几何推导 （最直观）和最小二乘/正交推导（最严谨）。下面我一步步给你讲清楚如何推导出来。

(2.1). 几何推导（最直观，推荐先看这个）

思路：向量投影就是 b 在 a 方向上的"影子"，即，它的长度是 b 在 a 方向上的分量（带方向），即||PS||，方向与 a 相同（或相反）。

向量 a 和 b 的夹角为 θ 。
b 在 a 方向上的标量分量（有向长度）是 ∣b∣cos⁡θ。
但点积定义：a⋅b=∣a∣ ∣b∣cos⁡θ，所以
向量投影必须沿着 a 的方向，所以要乘以 a 的单位向量。
因此向量投影为

这就是公式来源------完全来自点积的几何意义和单位向量的定义。

(2.2). 最小二乘/正交推导（更代数化，常用于证明唯一性）

思路：向量投影应该是 b 到直线 {ta∣t∈R} 上距离最近的点。这个最近点满足"误差向量垂直于直线"。

设向量投影为 p=ka （某个标量 k 倍的 a ）。
误差向量 b−p=b−ka 必须垂直于 a ，即点积为零：
因此

等价于最小化距离：对 k 求导并令为零，也得到相同结果。

小结

这个公式不是凭空记住的，而是自然从点积的几何定义、正交条件或最小距离原则推导出来的。
两种推导方式都非常基础，一旦理解了点积的含义（a⋅b=∣a∣∣b∣cos⁡θ ）和正交投影的几何图像，这个公式就"自己跳出来了"。
在更高维或子空间投影中，这个思路直接推广到正交投影矩阵，单向量时退化成上面的形式。

3) 右图：标量投影（结果是一个数）

它表示：b 在 a 方向上的"有符号长度"。

图上也写了几何等价式：

其中 θ 是 a 和 b 的夹角。

若 0∘<θ<90∘，cos⁡θ>0，标量投影为正（同向）
若 θ=90∘，cos⁡θ=0，标量投影为 0（完全垂直，投影没长度）
若 90∘<θ<180∘9，cos⁡θ<0，标量投影为负（投影方向与 a 反向）

4) 两者的关系（一句话记住）

comp：告诉你"沿 a 方向走多远"（一个数）
proj 告诉你"沿 a 方向走多远、往哪走"（一个向量）

5) 一个数值例子（把图上的公式算一遍）

取

点积：

标量投影：

向量投影：

你会看到：向量投影确实就在 a 的方向上（甚至这组数里刚好等于 a 本身）。

我们把这张图背后最容易"卡住"的点继续讲透：为什么这些式子等价、为什么会出现、以及图里 S 点到底在表达什么。

1) 为啥？

先看几何：右图里 PS 是把 PR=b 在 PQ=a 方向上的"影子"。

在直角三角形 △PRS 里：

斜边 PR 的长度是 ∥b∥
夹角在点 P（就是 a 与 b 的夹角 θ）
邻边 PS 的长度就是 ∥b∥cos⁡θ

而 标量投影 本质上就是"邻边长度（带符号）"，所以：

带符号 怎么来？

如果 θ>90∘，影子会落到 a 的反方向，cos⁡θ<0，就自然变负。

2) 为啥？

点积有一个经典几何定义：

两边除以 ∥a∥：

而右边我们刚证明就是，所以：

3) 为啥向量投影要除以？

这是最常见疑惑：怎么突然平方了？

关键是：向量投影必须在 a 的方向上，所以它一定长这样：

其中 k 是某个标量（比例系数）。

向量投影的长度（带符号）应该等于，而

ka 的长度是 ∣k∣ ∥a∥
更直接：把 ka 与 a 点积，会特别干净：

因为向量投影 与 a 平行，它在 a 方向上的分量就是它自己，所以：

因此

带回去：

这就是左图的第三个式子，是因为。

4) 图里的点 S 到底表达了什么？

S 是"垂足"：从 R 向 a 的直线做垂线，落点就是 S。

它表达两件事：

最短距离

在所有 a 方向的点 P+ta 里，S 是离 R 最近的那个（因为直角距离最短）。
误差正交

定义"误差向量" 。

图上就是从 S 指向 R 的那段（虚线那条方向）。

它满足：

这在最小二乘、正交分解里非常重要。

5) 记忆法：什么时候用 comp，什么时候用 proj？

你只关心"沿着 a 方向走多远"（长度、带正负）：用
你要得到一个真正的向量（可以再做加减、放进方程）：用

两者关系一句话：

向量分解与正交性解释

给定的公式描述了向量 b 在向量 a 方向上的投影分解，以及正交性质：

这是一个线性代数中的标准结果，将 b 分解为平行于 a 的部分（向量投影）和垂直于 a 的部分。下面我逐步解释其含义，并证明其成立。假设 a 和 b 是欧几里得空间中的向量，且 a≠0 。这里的表示转置（在向量上下文中等价于点积 a⋅ )。

1. 公式的含义

第一个等式 ：
- 这是一个向量加法分解：
  - 是 b 在 a 方向上的向量投影（平行分量），公式为。
  - 是 b 的剩余部分（垂直分量），它垂直于 a 。
- 几何上，这相当于将 b 分解为沿着 a 的"影子"和垂直于 a 的"偏差"。这在物理中常用于力或速度的分解（如斜面上的重力分力）。
第二个等式 ：
- 这表示垂直分量与 a 正交（点积为零）。
- 这是投影的本质属性：投影是 b 到 a 所在子空间的最短路径，剩余部分必须垂直于该子空间。

2. 证明过程

我将逐步推导第二个等式（正交性），因为它是非 trivial 的部分；第一个等式是 tautology（直接由加法定义得来）。

步骤 1 ：回忆投影公式。

（这里或。）
步骤 2 ：计算垂直分量。
步骤 3 ：计算（或等价的点积。
- 点积的线性性质：，其中。
步骤 4 ：简化表达式。
- 这里，所以相减为零。

因此，正交性成立。这证明了向量投影的唯一性和正确性（它是 b 到 a 方向的最优逼近）。