感知机简介
感知机(Perceptron)是1957年由Frank Rosenblatt提出的一种最简单的线性二分类模型,也是人工神经网络的奠基性单元。它接收多个输入特征,通过加权求和后加上偏置,再经过一个阶跃激活函数(如符号函数)输出 +1 或 -1 (0)的类别标签。
感知机采用误分类驱动的学习策略,仅当样本被错误分类时,才沿该样本方向更新权重。关键局限在于它只能处理线性可分问题;对于非线性可分数据(如异或问题),算法无法收敛。




多层感知机
多层感知机(Multilayer Perceptron, MLP) 是一种具有输入层、一个或多个隐藏层 和输出层的前馈神经网络,它通过非线性激活函数(如 ReLU、Sigmoid)连接各层,能够学习复杂的非线性映射关系 。与单层感知机不同,MLP 的隐藏层可以提取数据的中间特征表示,使模型具备更强的表达能力,从而解决线性不可分问题。
在 XOR 问题中,输入为两个二值变量(0 或 1),目标是输出它们的异或结果(当且仅当两者不同时为 1)。
由于 XOR 是典型的线性不可分问题,单层感知机无法用一条直线将其分类。而多层感知机通过引入一个隐藏层,将原始输入空间映射到新的特征空间,在该空间中数据变得线性可分。例如,隐藏层可以分别检测"两个输入都为 0"、"两个输入都为 1"等模式,最终输出层组合这些中间判断结果,实现对 XOR 的正确分类。这体现了 MLP 通过层次化特征学习突破线性限制的能力。
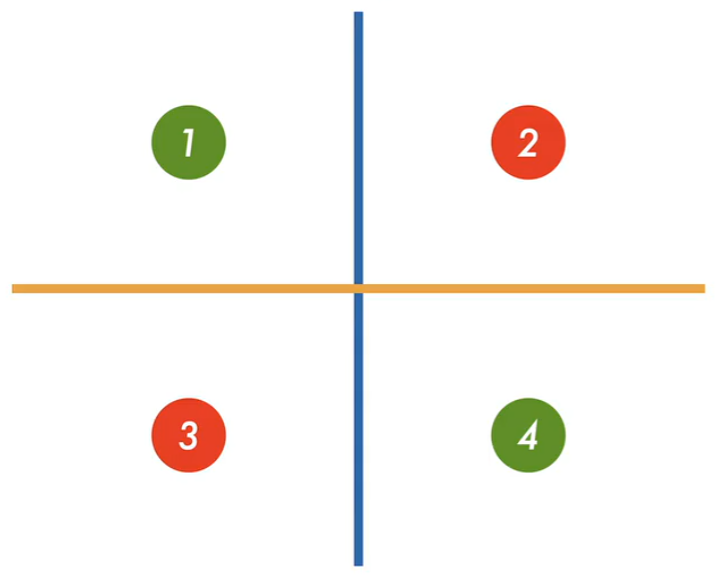
先学习蓝色线,再学习黄色线。异或得出最终结果。
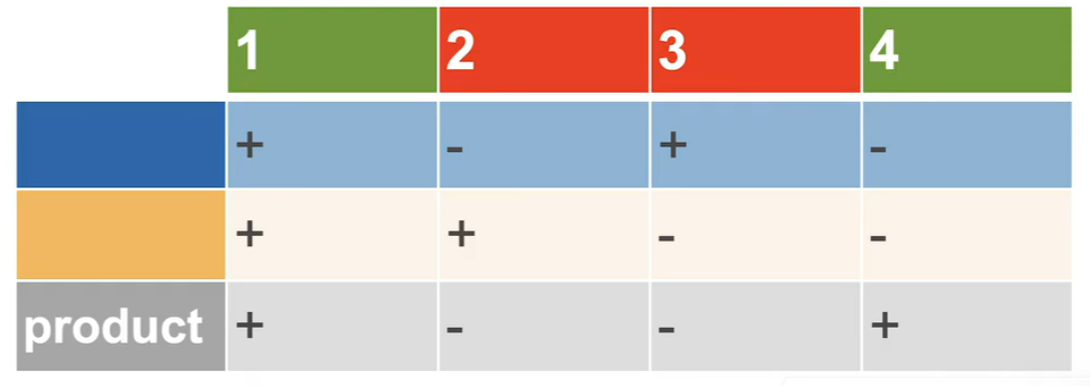
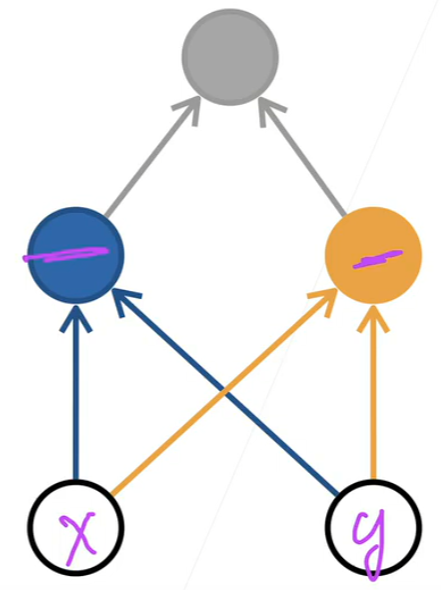
隐藏层
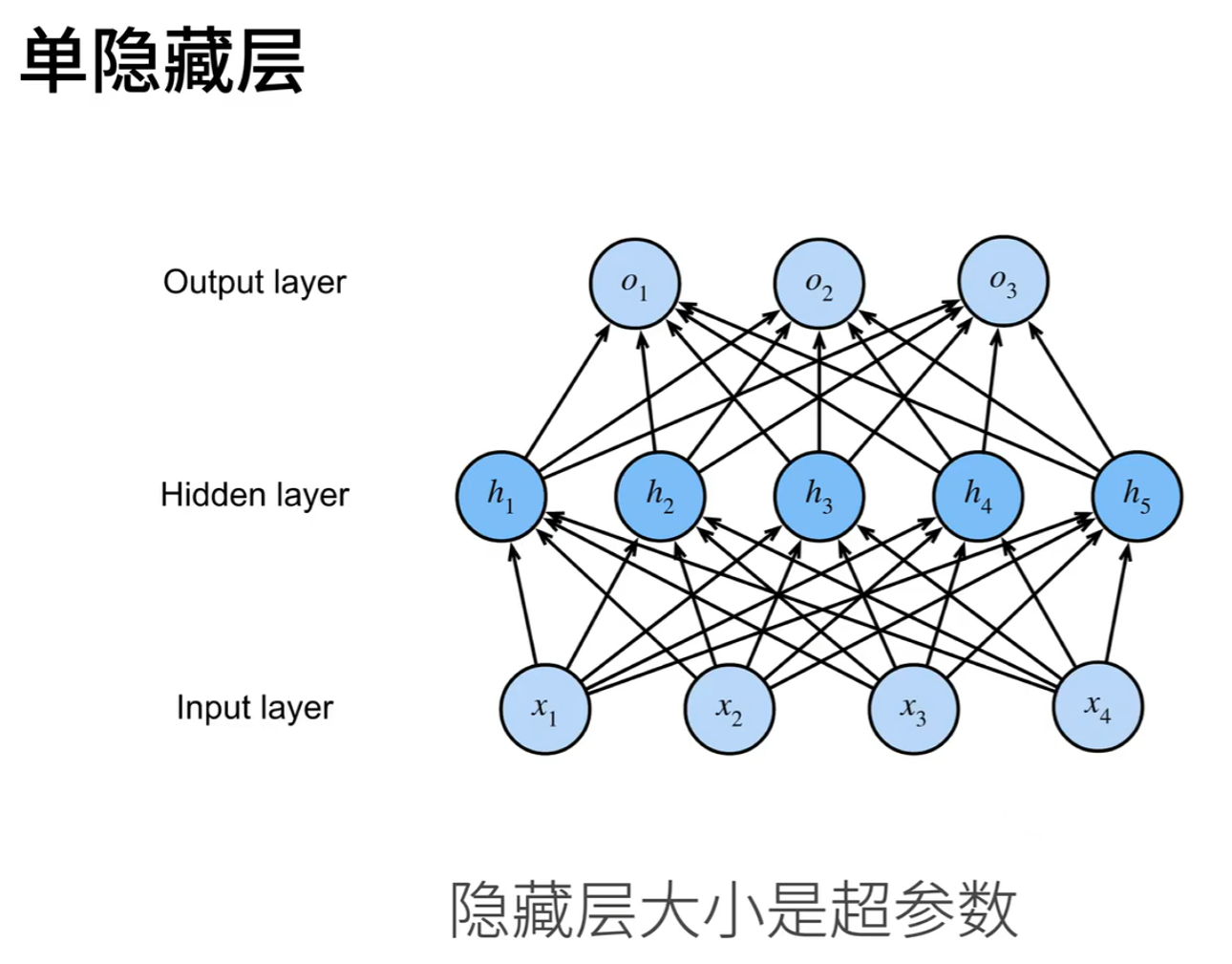
隐藏层是神经网络中位于输入层和输出层之间的中间层,它的主要作用是从原始输入数据中自动学习并提取更高层次的抽象特征。
通过将输入信号经过加权求和、加上偏置,再通过非线性激活函数 (如 ReLU 或 Sigmoid)进行变换,隐藏层能够将数据映射到一个新的表示空间。在这个新空间中,原本无法用直线分开的复杂模式可能变得线性可分,从而使整个网络具备解决非线性问题的能力。隐藏层的数量和每层的神经元个数决定了模型的表达能力和复杂度。
注:
激活函数是人工神经网络中一个关键的组成部分,用来引入非线性特性到神经网络模型中,同时还可以解决梯度消失/爆炸等问题。
RELU(Rectified Linear Unit)是一种常用的激活函数,定义为 f(x) = max(0, x)。它的特点是对于所有正输入,输出等于输入;对于负输入,输出为零。
对于其使用的时机,一般情况下是线性之后,下一层之前,来添加非线性特性,Conv2d → BN → 激活 → (Dropout) → Pool / 下一层。


代码
使用多层感知机配合了RELU激活函数,实现简单的MNIST手写数字数据集分类问题。
完整代码:
python
import torch
from torch import nn
from torch.utils.data import DataLoader
from torchvision import datasets, transforms
data_root = r'D:\pycode\write\Minist1\w1'
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])
train_dataset = datasets.MNIST(root=data_root, train=True, download=False, transform=transform)
test_dataset = datasets.MNIST(root=data_root, train=False, download=False, transform=transform)
batch_size = 256
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False)
net = nn.Sequential(
nn.Flatten(), # 将 [B, 1, 28, 28] 展平为 [B, 784]
nn.Linear(28 * 28, 128), # 隐藏层:784 → 128
nn.ReLU(),
nn.Linear(128, 10) # 输出层:128 → 10(logits)
)
def train(model, loader, criterion, optimizer, device):
model.train()
total_loss = 0
correct = 0
total = 0
for data, target in loader:
data, target = data.to(device), target.to(device)
optimizer.zero_grad()
output = model(data)
loss = criterion(output, target)
loss.backward()
optimizer.step()
total_loss += loss.item()
pred = output.argmax(dim=1)
correct += pred.eq(target).sum().item()
total += target.size(0)
return total_loss / len(loader), correct / total
def test(model, loader, criterion, device):
model.eval()
total_loss = 0
correct = 0
total = 0
with torch.no_grad():
for data, target in loader:
data, target = data.to(device), target.to(device)
output = model(data)
loss = criterion(output, target)
total_loss += loss.item()
pred = output.argmax(dim=1)
correct += pred.eq(target).sum().item()
total += target.size(0)
return total_loss / len(loader), correct / total
if __name__ == "__main__":
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(f"Using device: {device}")
model = net.to(device)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
epochs = 10
for epoch in range(1, epochs + 1):
train_loss, train_acc = train(model, train_loader, criterion, optimizer, device)
test_loss, test_acc = test(model, test_loader, criterion, device)
print(f"Epoch {epoch:2d} | "
f"Train Loss: {train_loss:.4f}, Acc: {train_acc:.4f} | "
f"Test Loss: {test_loss:.4f}, Acc: {test_acc:.4f}")
print("\n训练完成!")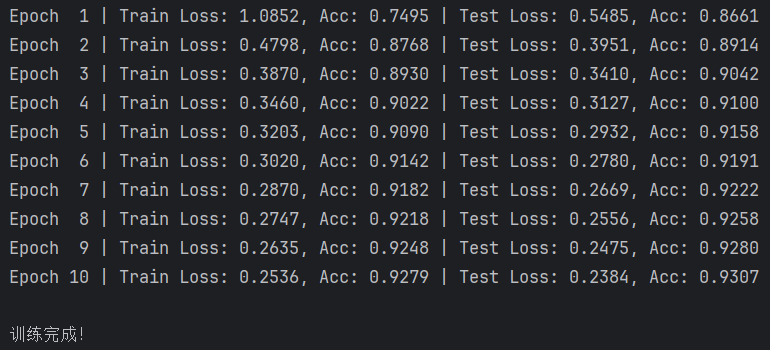
python
net = nn.Sequential(
nn.Flatten(), # 将 [B, 1, 28, 28] 展平为 [B, 784]
nn.Linear(28 * 28, 128), # 隐藏层:784 → 128
nn.ReLU(),
nn.Linear(128, 10) # 输出层:128 → 10(logits)
)| 步骤 | 输入形状 | 操作 | 输出形状 |
|---|---|---|---|
| 原始输入 | [1, 1, 28, 28] |
--- | --- |
→ Flatten() |
[1, 1, 28, 28] |
展平 | [1, 784] |
→ Linear(784,128) |
[1, 784] |
线性变换 | [1, 128] |
→ ReLU() |
[1, 128] |
非线性激活 | [1, 128] |
→ Linear(128,10) |
[1, 128] |
线性变换 | [1, 10](logits) |
虽然只有"两层",但它已经是多层感知机(Multilayer Perceptron),因为包含了至少一个隐藏层 + 非线性激活------这是 MLP 的核心定义。