1.观察底层
下面看看map和set的底层,map底层是一个rb_tree,set底层也是一个rb_tree:
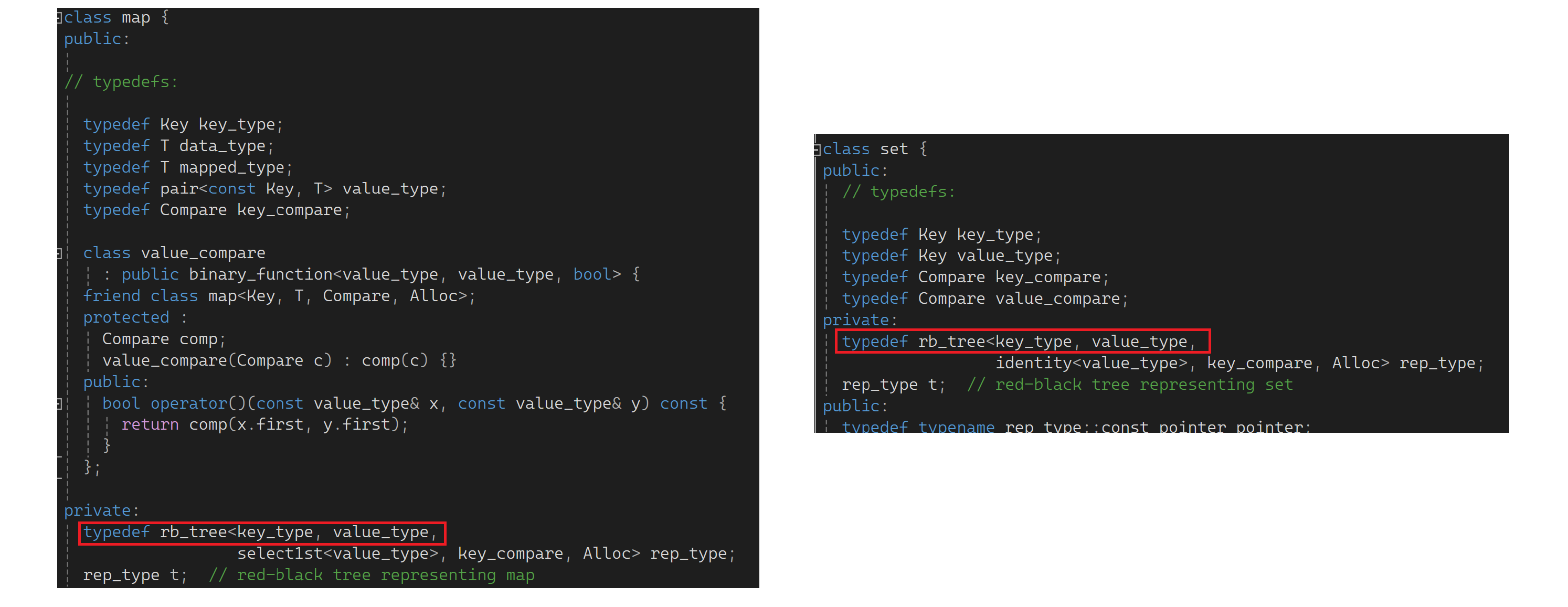
按我们的理解觉得map底层是一个KV结构,set是一个K结构的红黑树,实际不是这样的。发现set和map都是KV结构的红黑树:

发现map的k是Key,v是pair;set的k是Key,v也是Key。
2.封装
下面看看如何达到封装,首先看看源码:按我们的以前的理解我们包了map和set的头文件,但实际从源码角度map和set里面没有特别实质的内容,比如拿set来说:
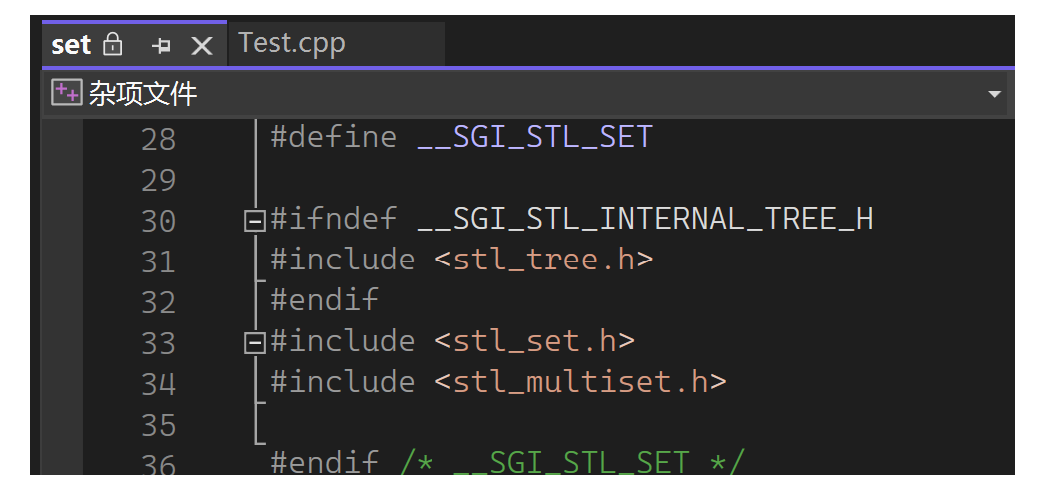
它实际上包含了一些头文件,它的核心实现是stl_tree.h,这里面就是红黑树的实现。也发现set里既有set,也有multiset,所以multiset可以不另外包头文件,因为在set里面。把三个核心弄出来:

这里想知道的重点有以下:首先之前我们的理解是set是k,map是k-v,我们觉得它应该用两棵树,一棵树实现k的,一棵树实现k-v的。但实际它们没有用两棵树,它们用了同一颗树,那同一颗树怎么做到即可存map也可存set呢?看一下set.h的核心:
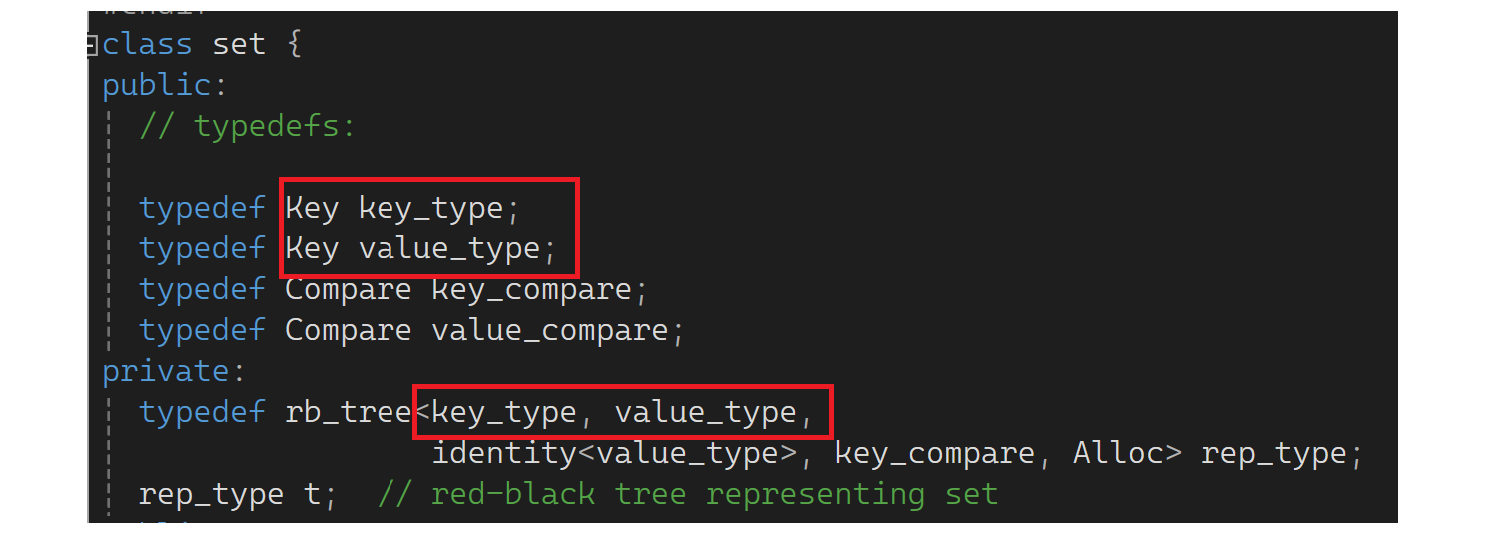
set这弄的红黑树是一个kv结构的,这写的是key_type和value_type,但从typedef角度来说都是Key。再看一下map.h核心:
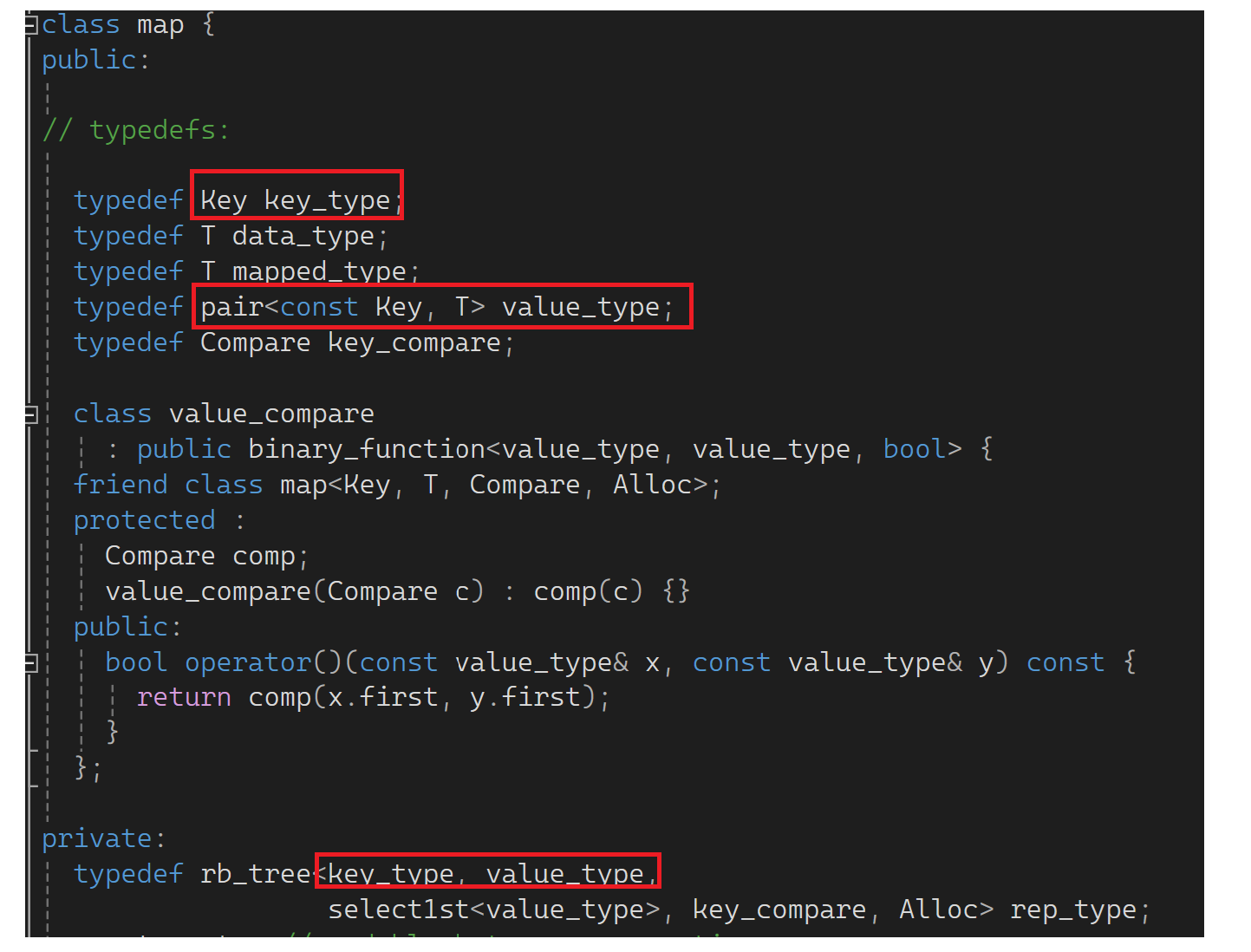
map这也弄的是kv结构的红黑树,这的key_type是key,value_type是个kv的pair。一个是<k,k>,另一个是<k, pair<k,v>>,想理解这里还要看一下tree.h:
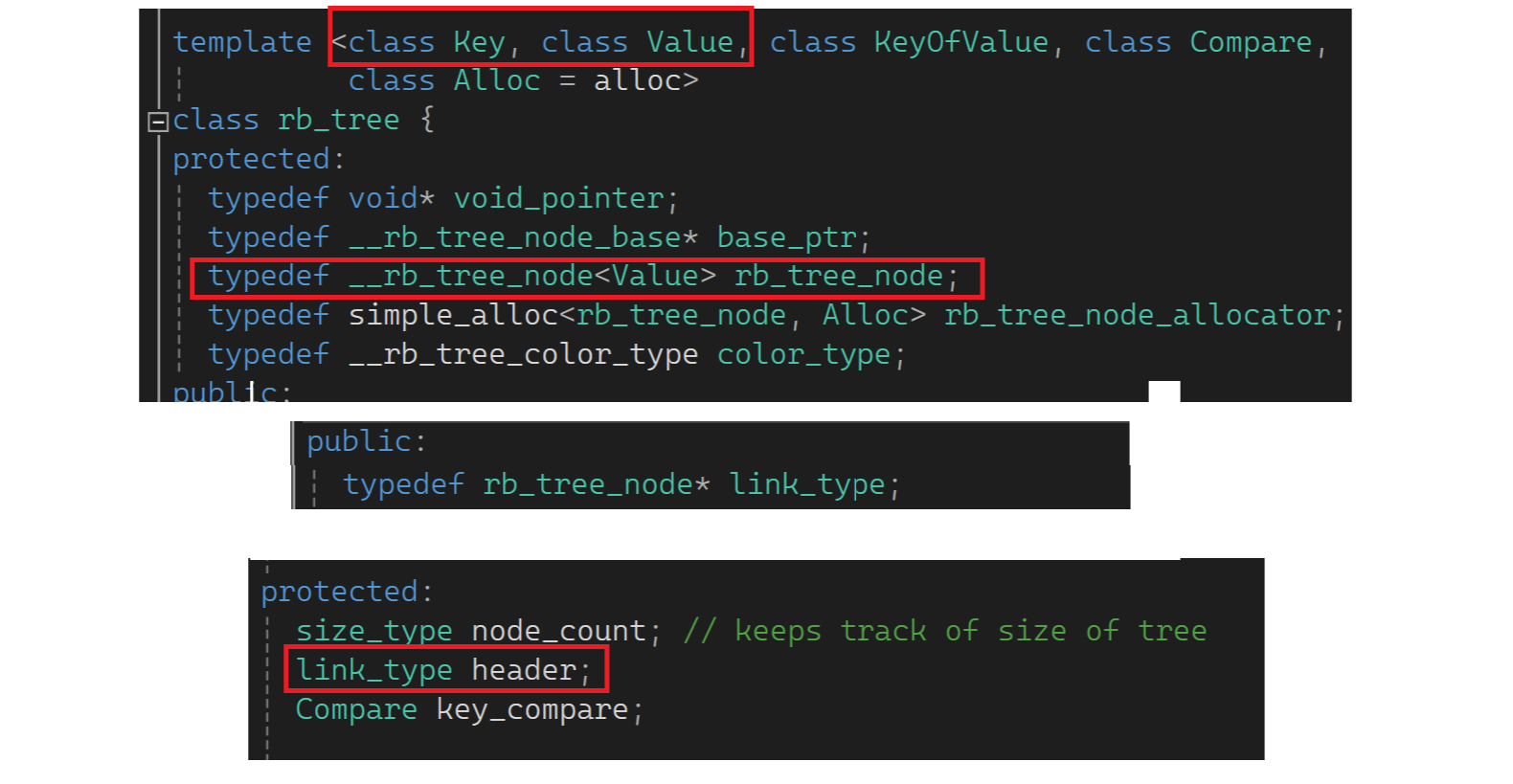
这里有个link_type的header,link_type又是rb_tree_node*类型的指针。再观察会发现这个树的结点里存的类型是第二个模板参数,对于rb_tree是value,但这个value不是真value。对于map而言这个value是个pair,意味着对map而言树的结点存的是pair;对于set而言树的结点存的是个k。意味着rb_tree真正决定树里面或结点里面存什么是由传的第二个模板参数决定的(继承了三叉链):
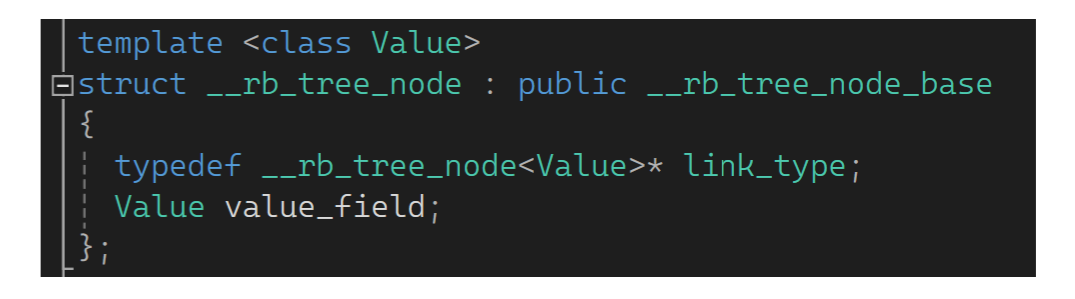
那这样传第一个key有什么用?

比如对于find接口,不能说去找pair,找的是k,这也是为了统一的适配。
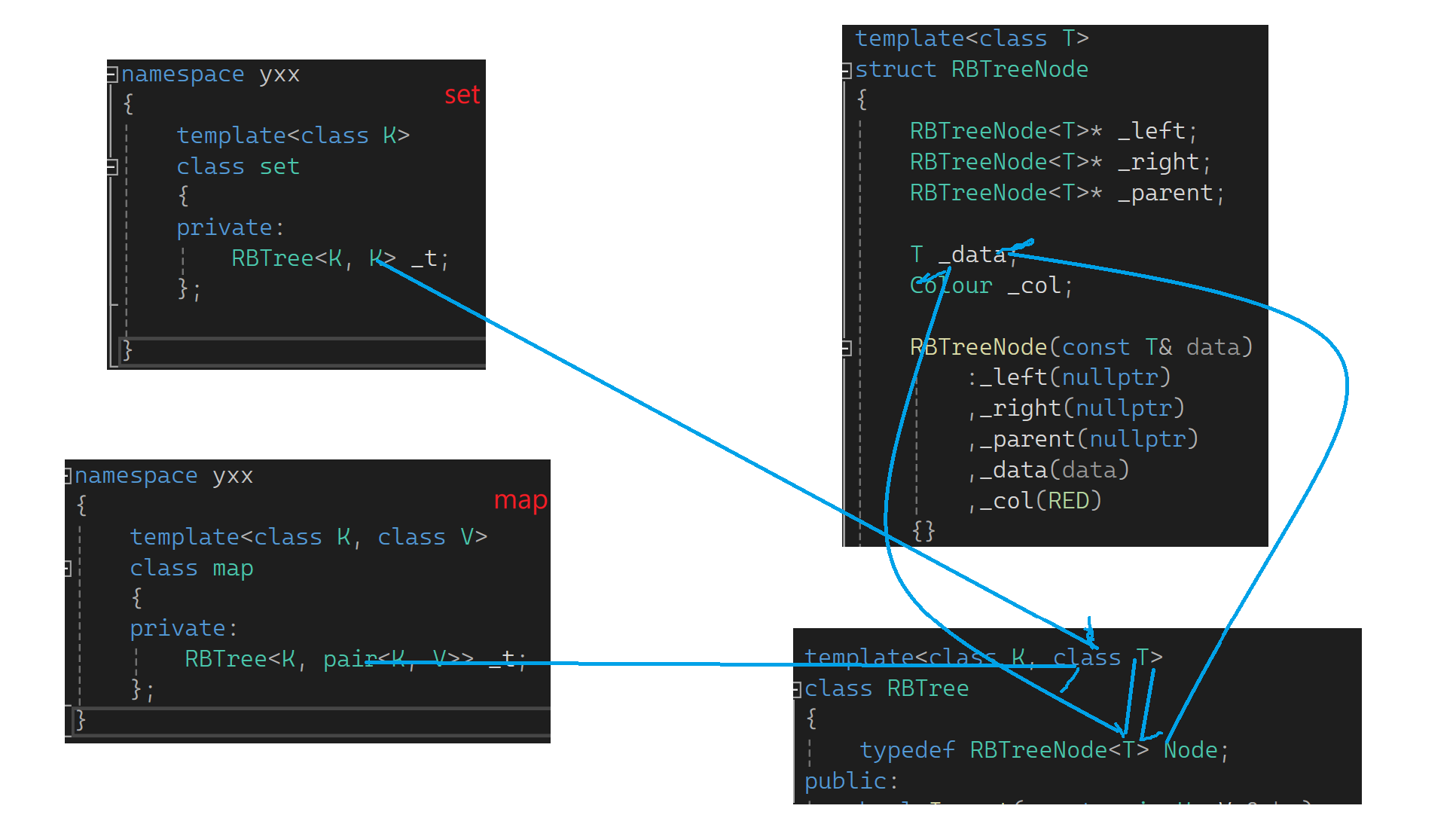
现在把刚才的框架照样子弄一个出来(复用前面RBTree.h,改成适合的样子),把V改为T,要不然有点取名混淆:
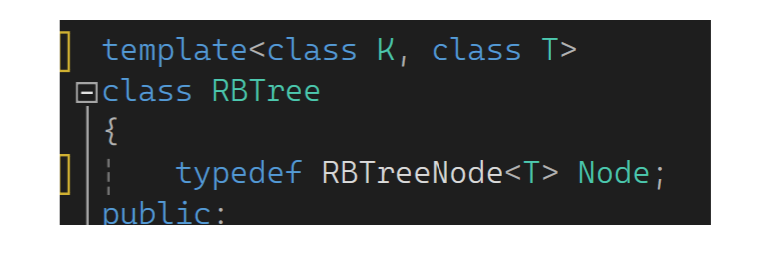
K是为了find那些好弄,T是为了决定树的结点里面存什么。再改下面:

上面改完后就不是写死的pair了,可改成T类型的数据,数据是什么我们也不知道。可认为在红黑树这一层走了一个泛型,以前实现红黑树都是确定的k或kv的pair,现在也不知道具体是哪一个了。再进一步封装一下,写个Mymap.h和Myset.h:
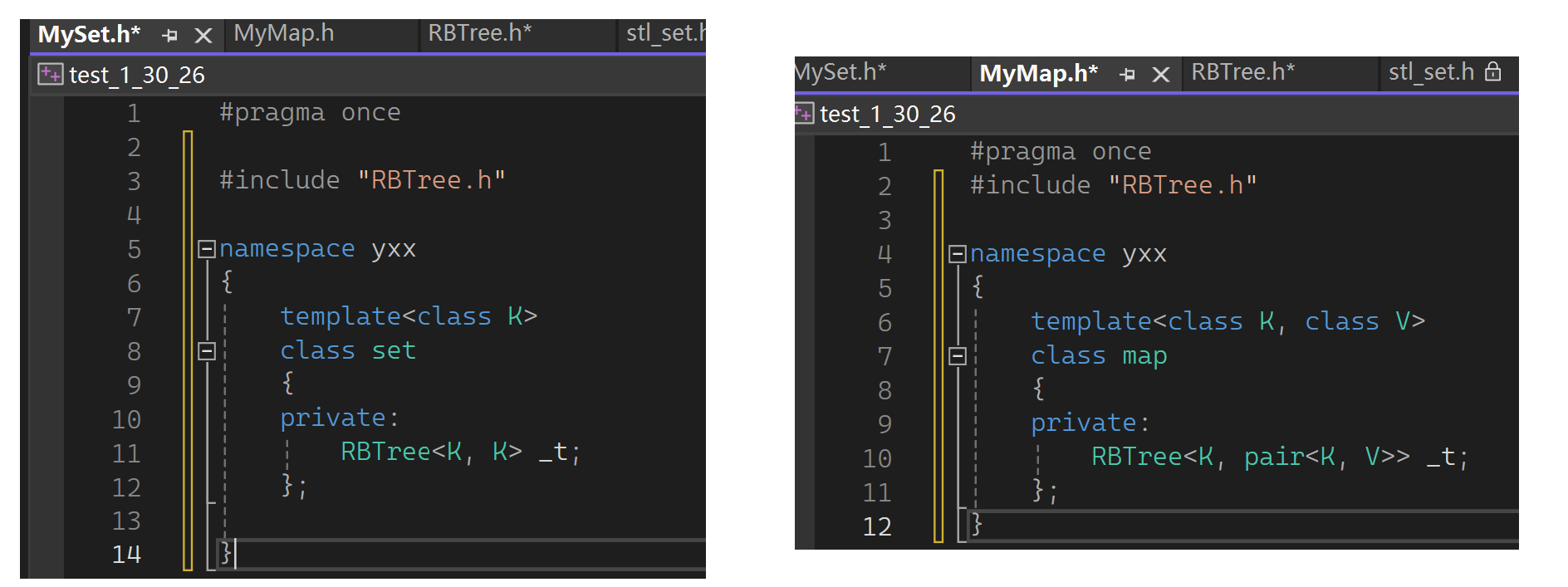
再简化看一下:
但这个东西就这样轻松解决了吗?这里还有很多坑,先编译一下:
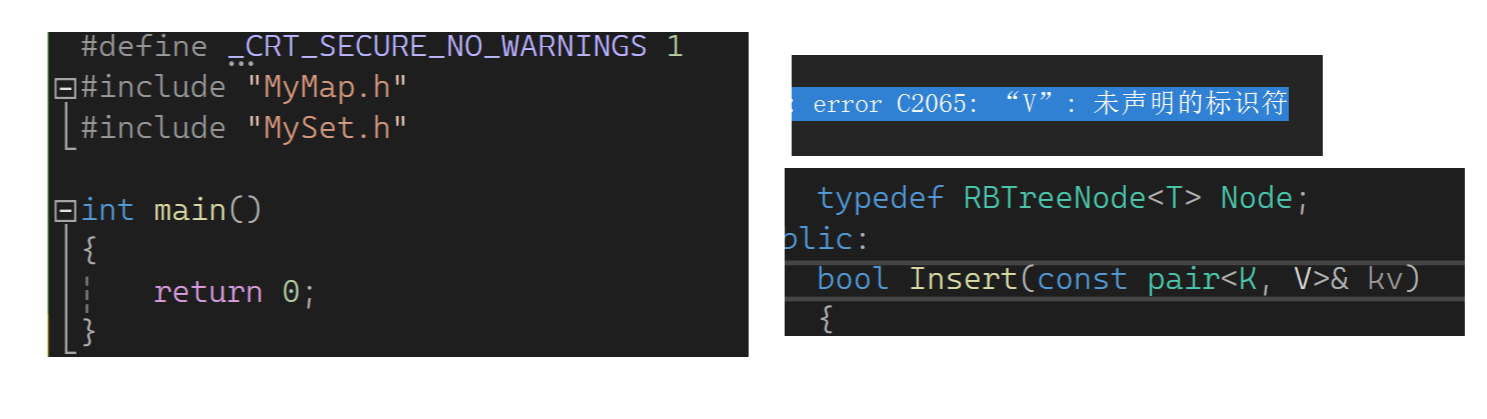
看到有一些问题,模板参数这里已经是T了,这里就不是KV了,改了后insert这的模板参数应该用T(对set来说插入K,对map来说插入pair)。因为RBTree这一层相当于是适配的泛型,不知道存的是k还是pair,T是什么存的就是什么,所以都改一下:
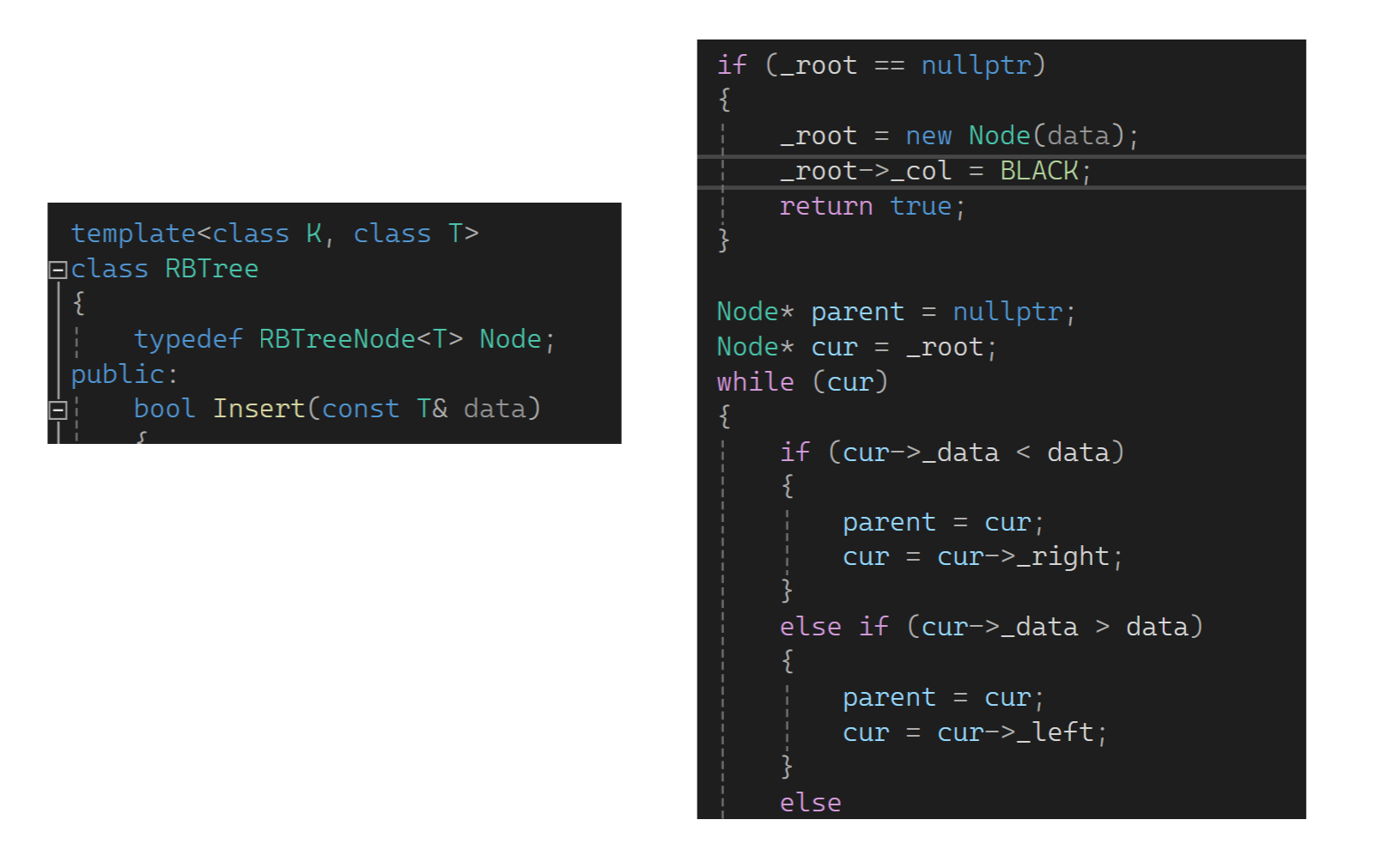
以前存pair时知道用first比,现在的问题是插入大了往左走,小了往右走没有问题,但可以直接这样比较吗?对于set没什么问题,就是直接用data进行比较,对于setT实例化是K,就是K的比较。对于map来说T是pair,比较是用pair比的,更期望用pair的first来比较:

库里面重载了一些pair的比较,但这里的比较不是我们想要的比较方式,我们期望的是按照first去比较,但库里面不是。比如:

上图是first小就小或second小就小来比较。那如何解决?可以用仿函数,增加一个KeyOfT(T中取Key):
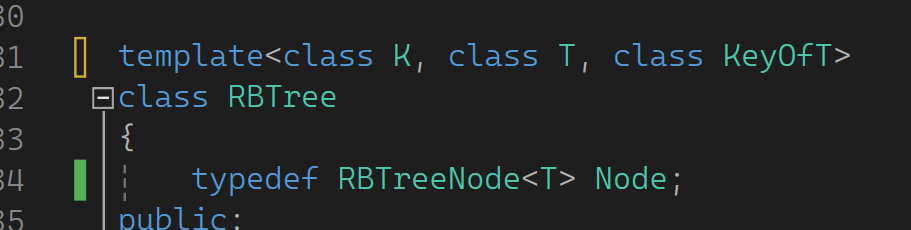
KeyOfT这里传进来一个仿函数,那怎么传呢?这里定义一个内部类,Map中定义MapKeyofT,它的责任是把Map传给T的值(pair)中的first取出来:
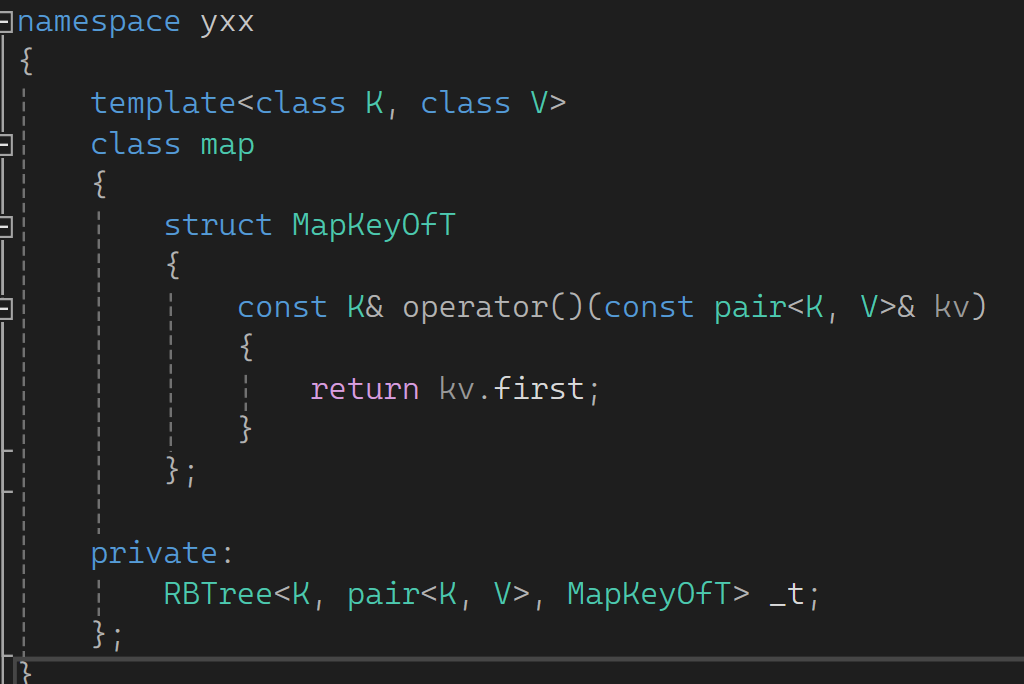
同时为了进行匹配底层同一个树,set中也定义SetKeyOfT,对于set而言传给T的是Key,就对照着返回就行:
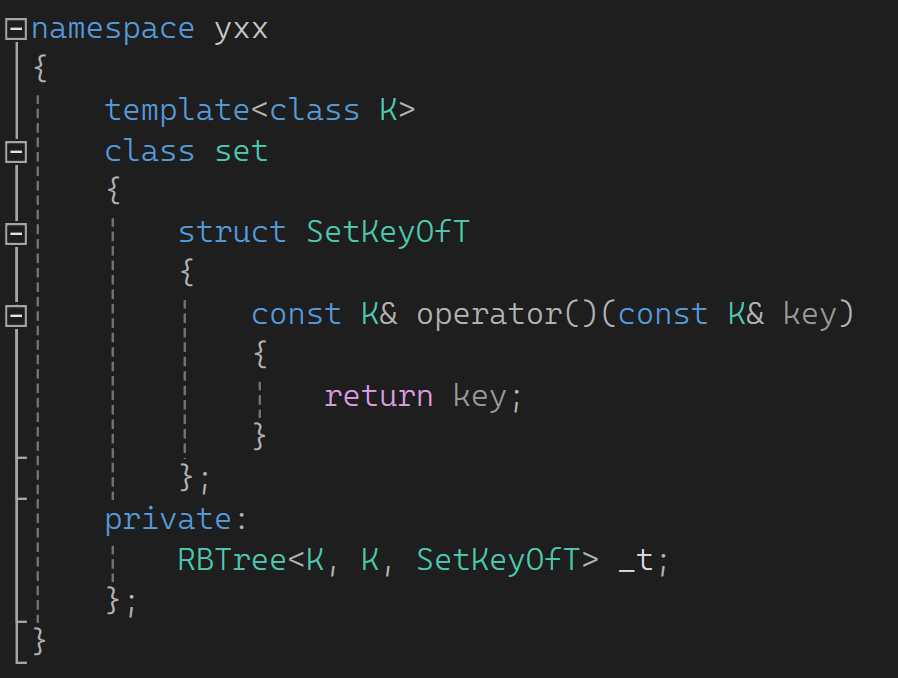
用的时候反正也不知道KeyOfT是什么,只知道能把data中的T取出来:

来看下图理解一下:
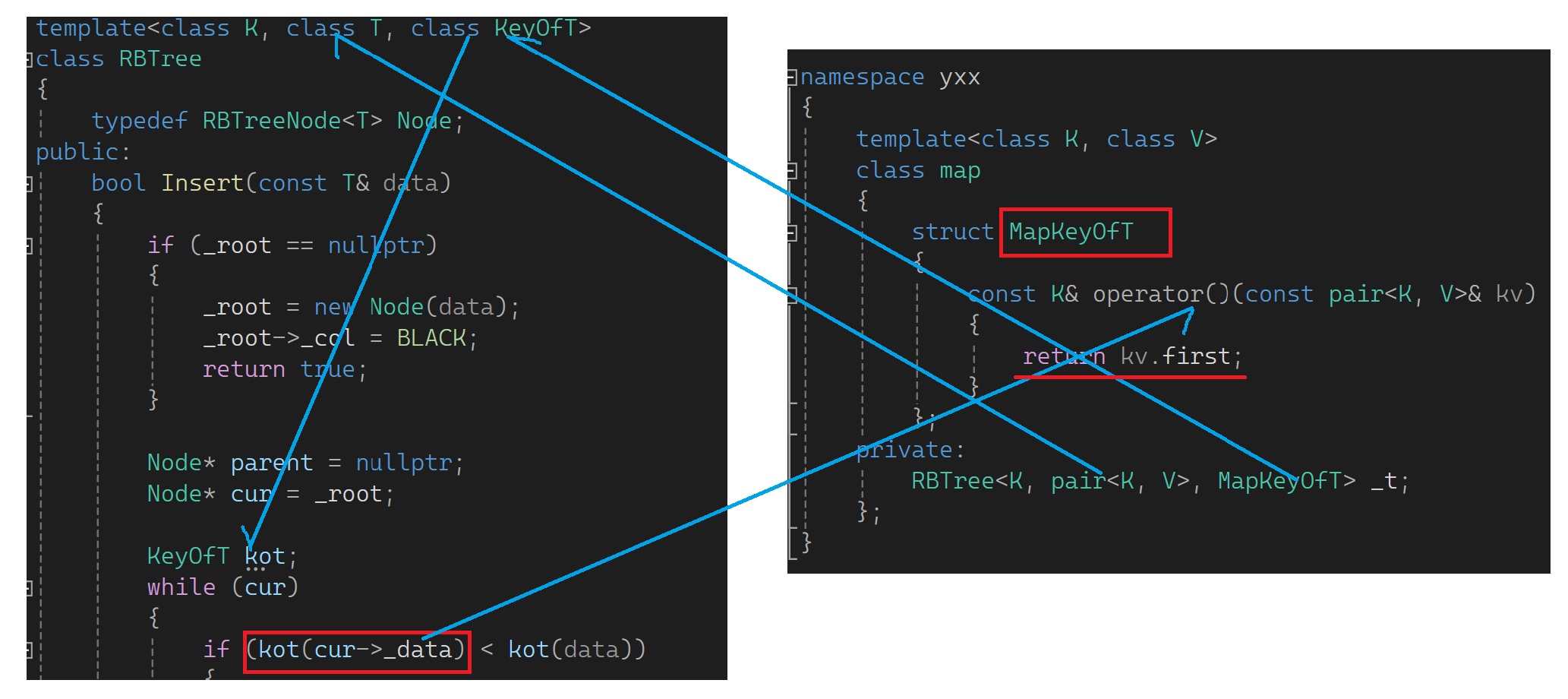
这的仿函数和之前不一样的地方在于没有说直接比较,而是是把T对象中的key成员取出来。
下面实现find(为了和后面迭代器有联系这返回结点指针):

为了测试一下目前写的是否可以跑,先在外面写一套insert:

下面来测试一下(仅有public的问题):
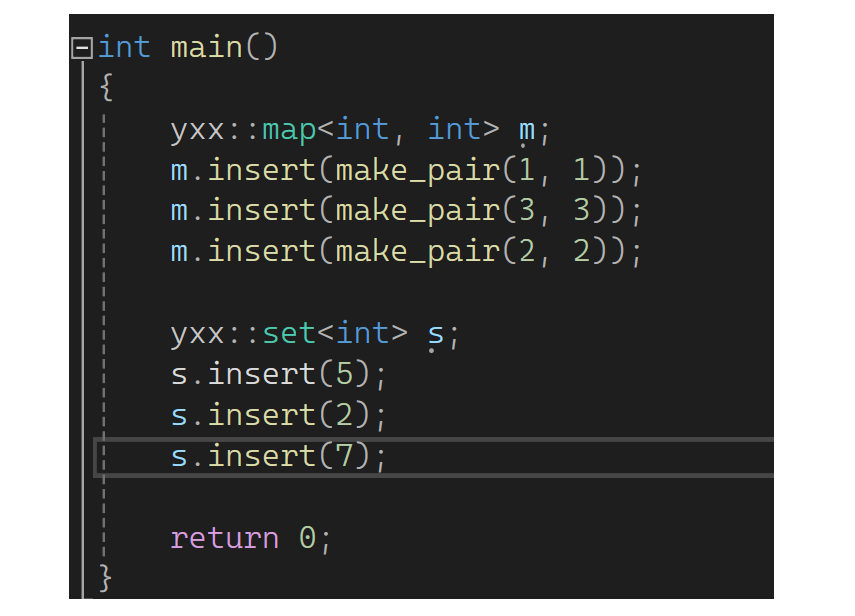
下一步来看看迭代器,先看看库里的set:

set里面是ret_type的迭代器,rep_type就是rb_tree,这里只是typedef了一下。再看下图:

树里迭代器是个类,可以理解到这的正向迭代器和链表那的迭代器是很像的,是一个自定义类型。链表的自定义类型里封装的是结点的指针,那这里是什么呢?
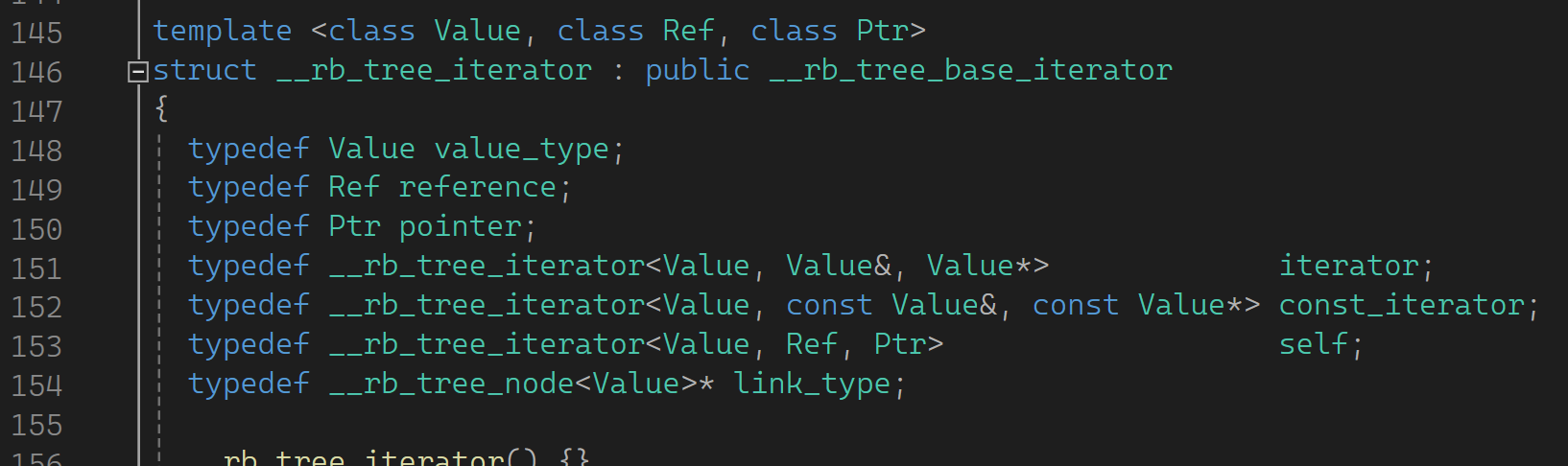
这里封装了两层,弄了一层继承。再看下图:
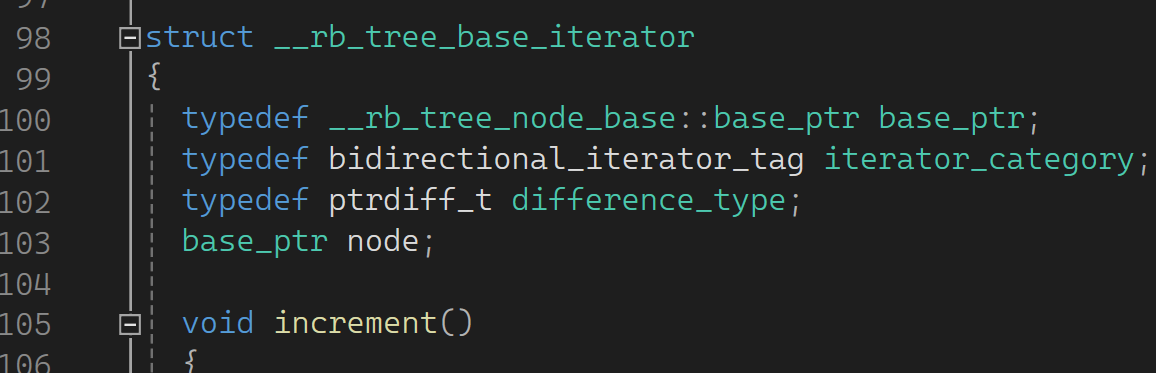
这里定义了一个base_iterator,它里面有一个结点的指针。还有下图:

operator*返回结点里的value_filed,对于set而言value_filed是key,对于map而言,value_faild是pair。树这里别的好说,麻烦的是++和--:
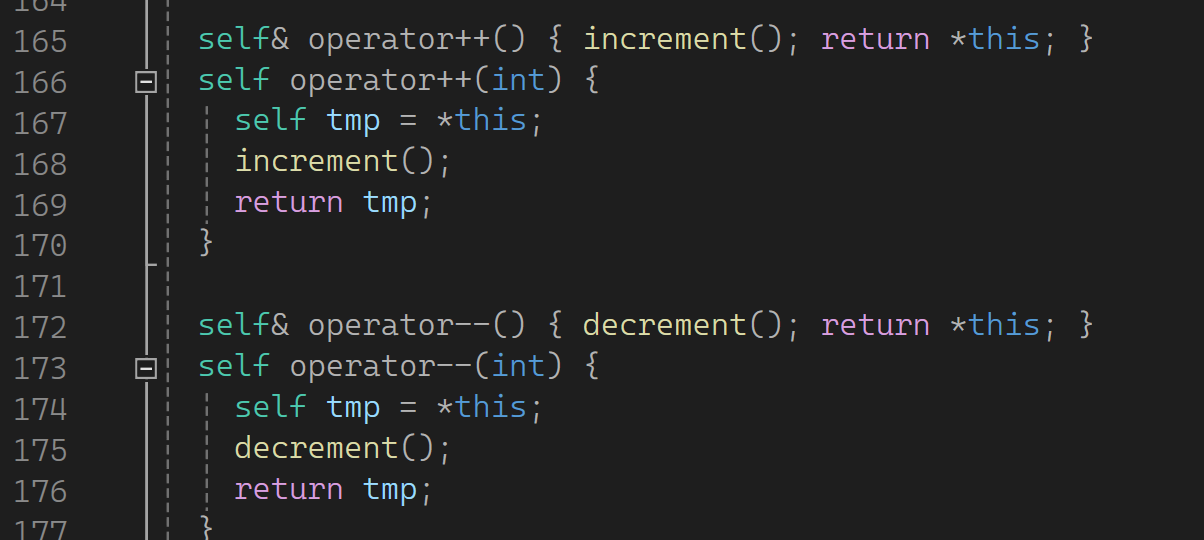
拿set举例,这里大概是这个样子:
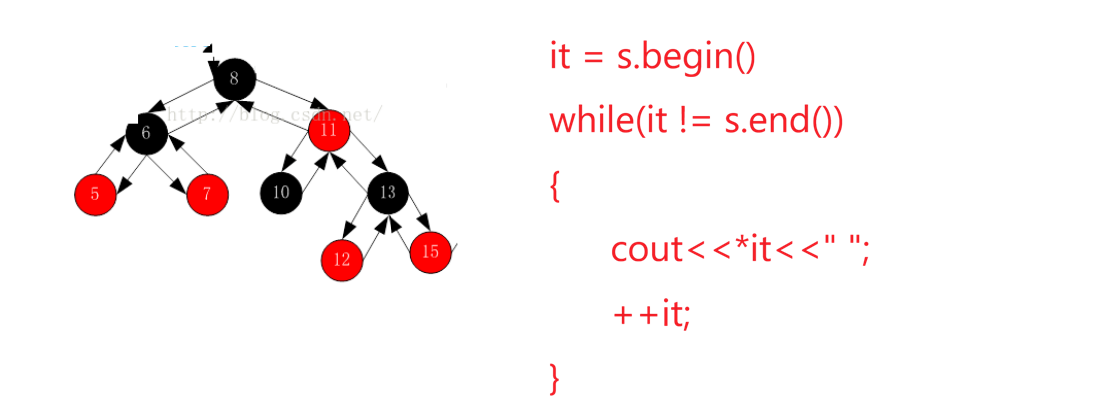
begin返回的必须是这棵树的最小值,搜索树里最左结点就是最小值,也就是中序的第一个。看看库里是怎么样的:
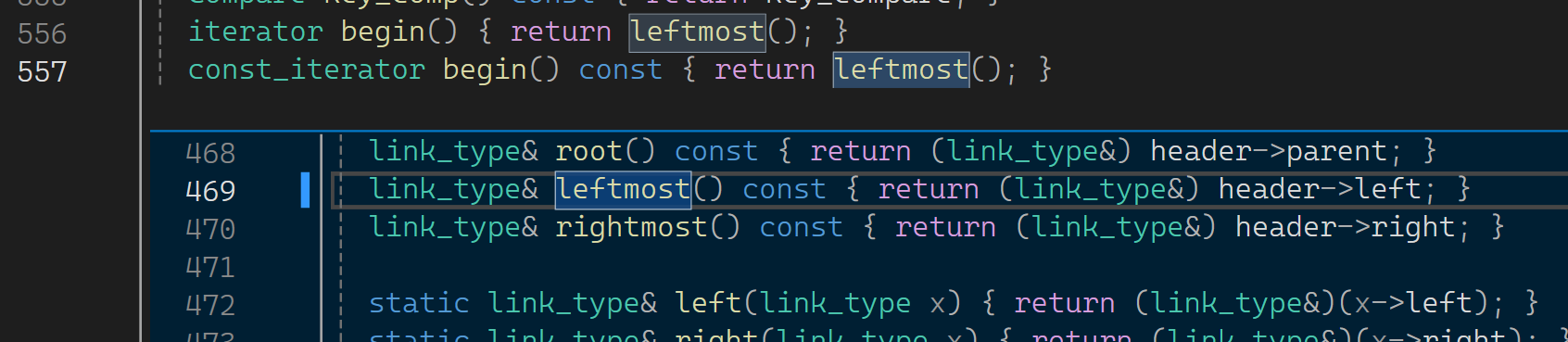
库里的begin返回的是一个leftmost,速览定义可以看到它返回header的left(会和我们的实现不一样)。先看看++怎么走?我们相当于不借助栈,完成中序的非递归。比如现在it在8这个位置,++怎么找到下一个结点:
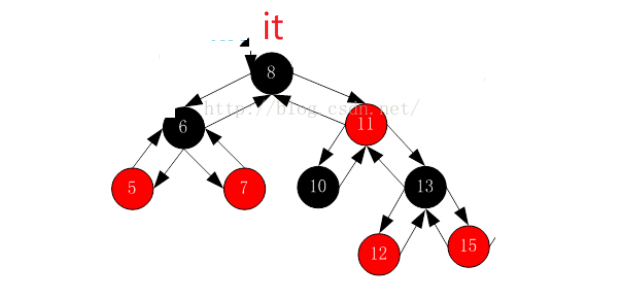
如果右不为空,就访问右树的最左结点。上述是一个简单的场景,再看一个复杂的场景:
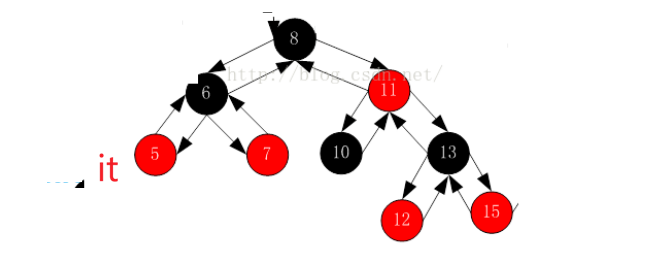
如果it在5这个位置,右边是空的呢?要访问的是祖先(不空是父亲),因为右为空预示着我自己访问完了,而中序是左子树,根,右子树。意味着我是父亲的左,下一个访问父亲,++就走到6了:
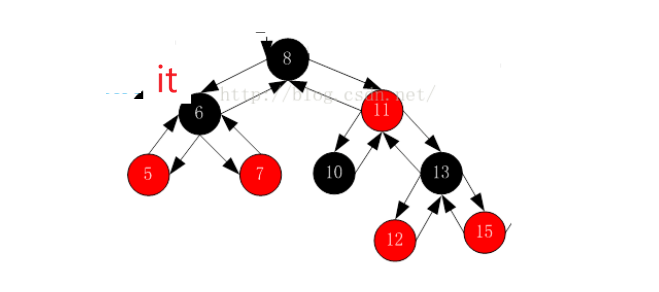
现在右不为空,访问右树最左结点到7了:
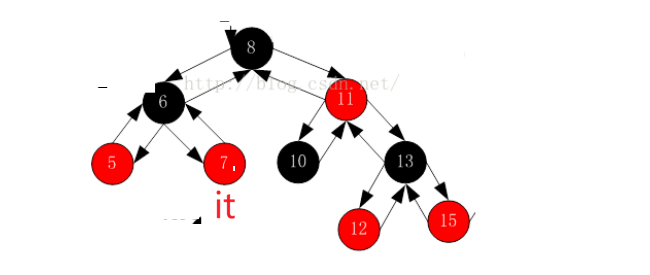
现在右为空,并且我是父亲的右,意味着我完了父亲也完了,就再往上找到6,6是8的左访问过了就在访问8:
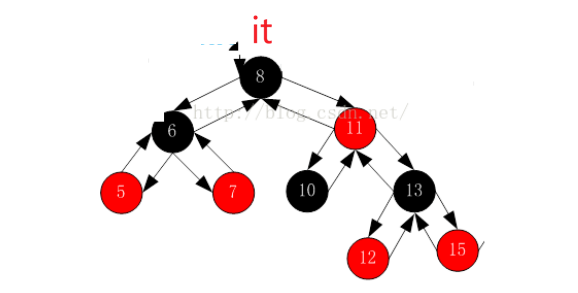
意味着右为空,下一个访问的是孩子是父亲左的那个祖先。最后不断走,找不到父亲就结束了,所以end可以用空代替。现在先来搭个架子:

现在实现++,最开始整体的大逻辑是begin返回了第一个位置的迭代器,然后如果_node的right不为空,找右子树的最左结点,找到后给_node。else就是右为空,定义cur等于当前结点,然后去找它的父亲,在父亲不为空的情况下,如果cur等于父亲的左,下一个要访问的就是父亲;如果cur是父亲的右,就沿着往上走。else中while结束后有两种情况,要么cur等于父亲的左,也就找到了孩子是父亲左的那个祖先结点,就是下一个要访问的结点;要么父亲是空。无论哪一种情况都让_node指向父亲,最后返回迭代器本身:
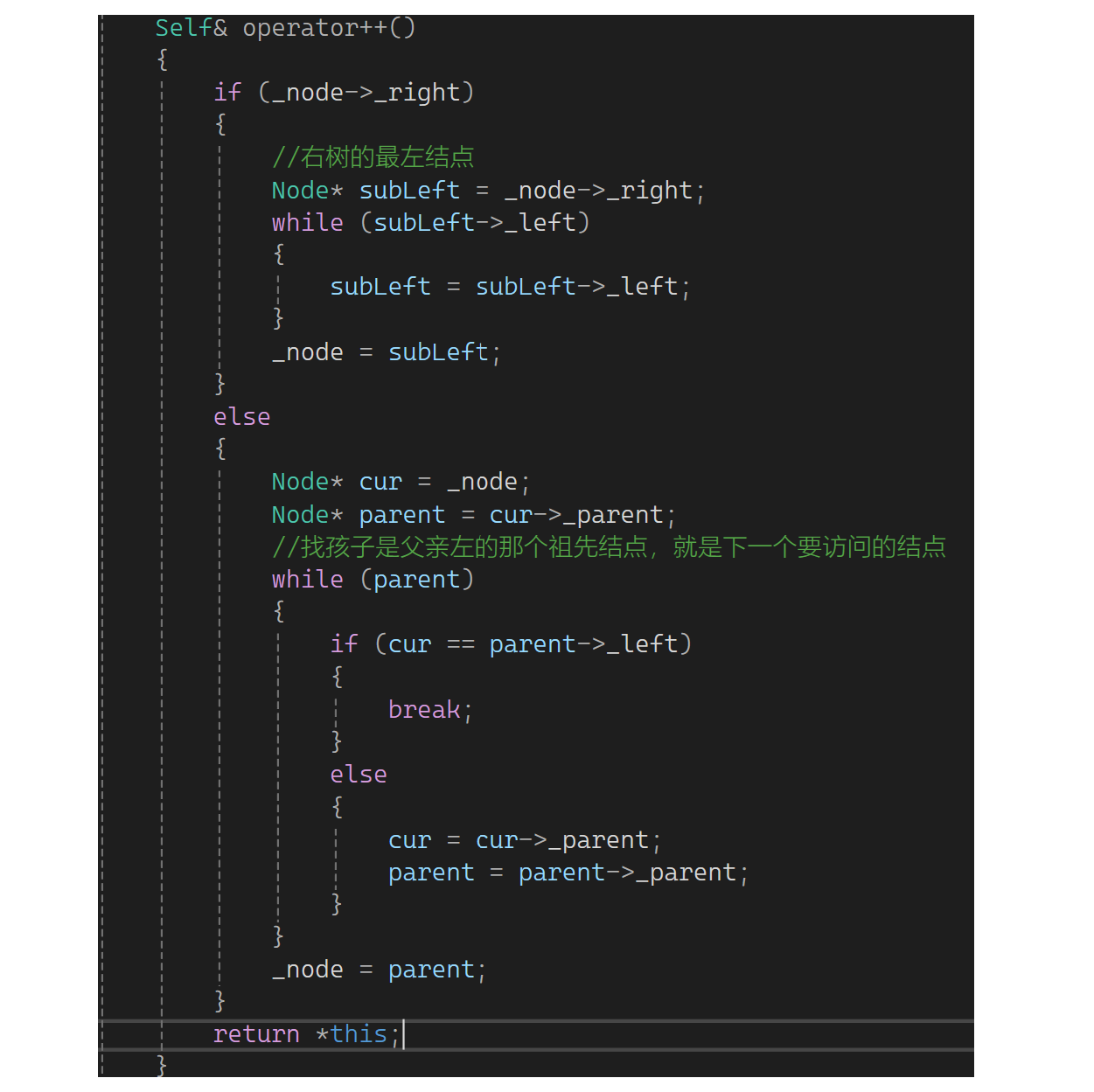
再实现一下operator!=:
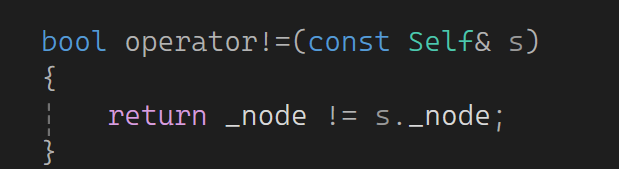
再补充一下begin和end:
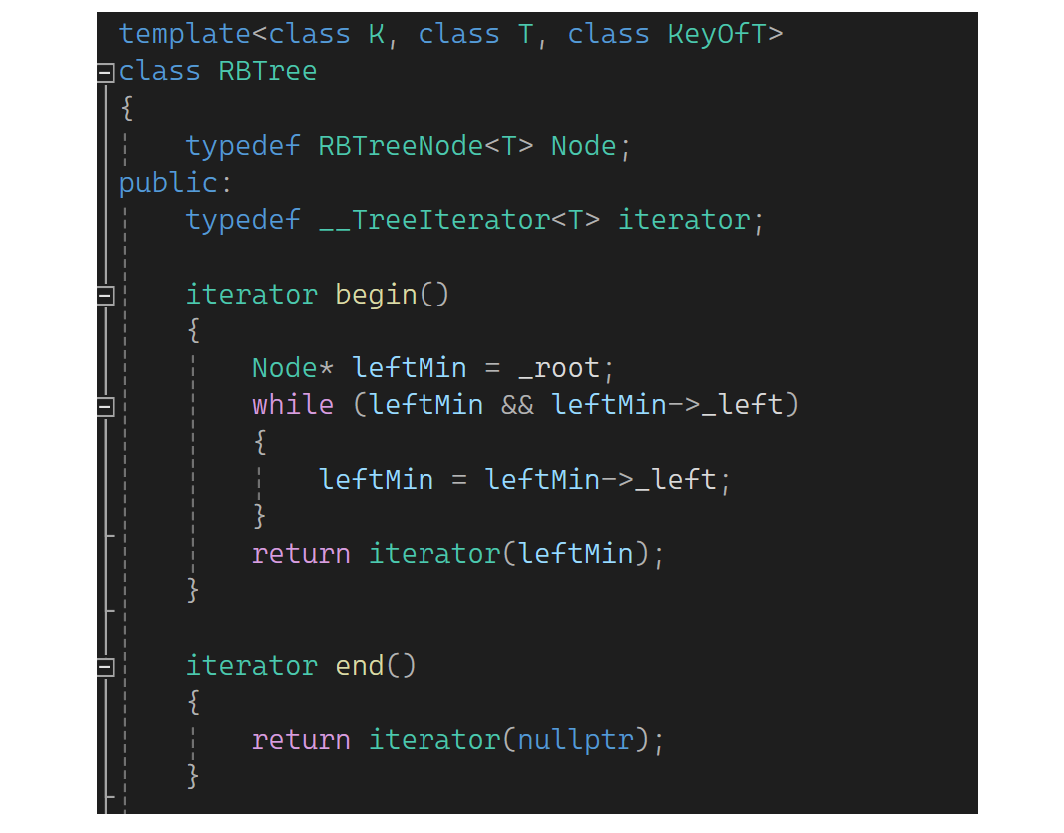
下面跑一下迭代器,先把set走通:
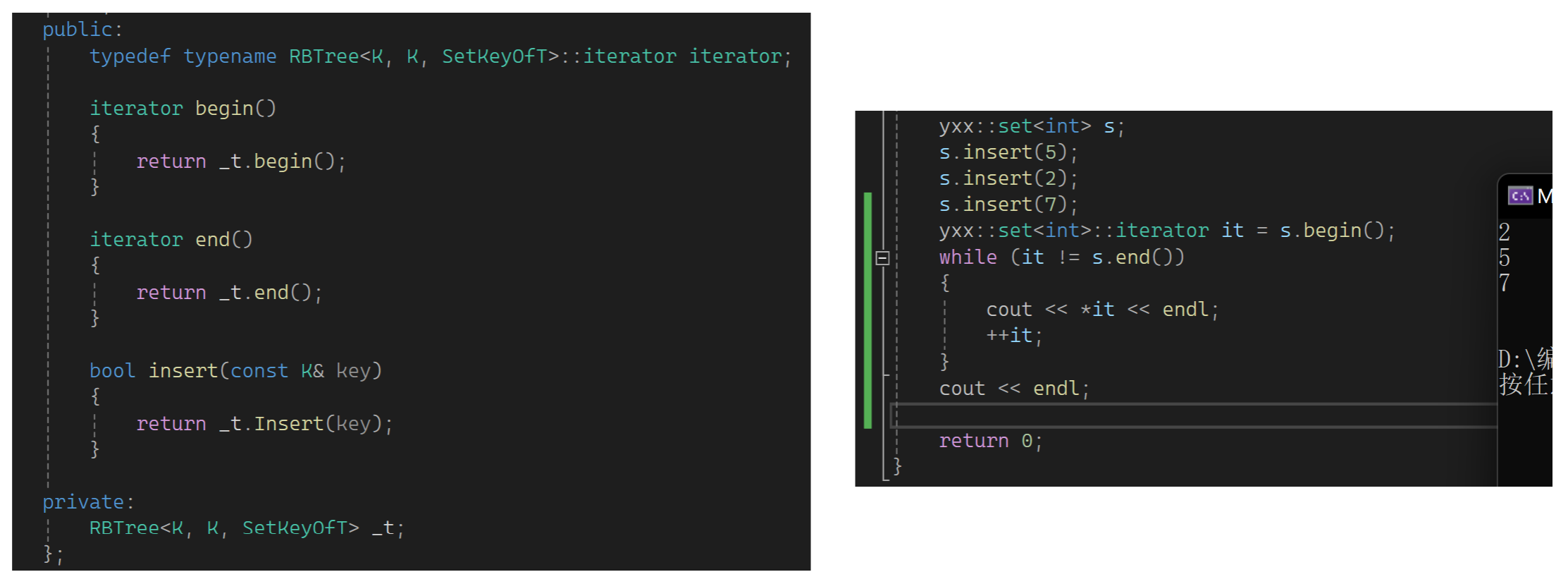
完成后再把map完善一下:
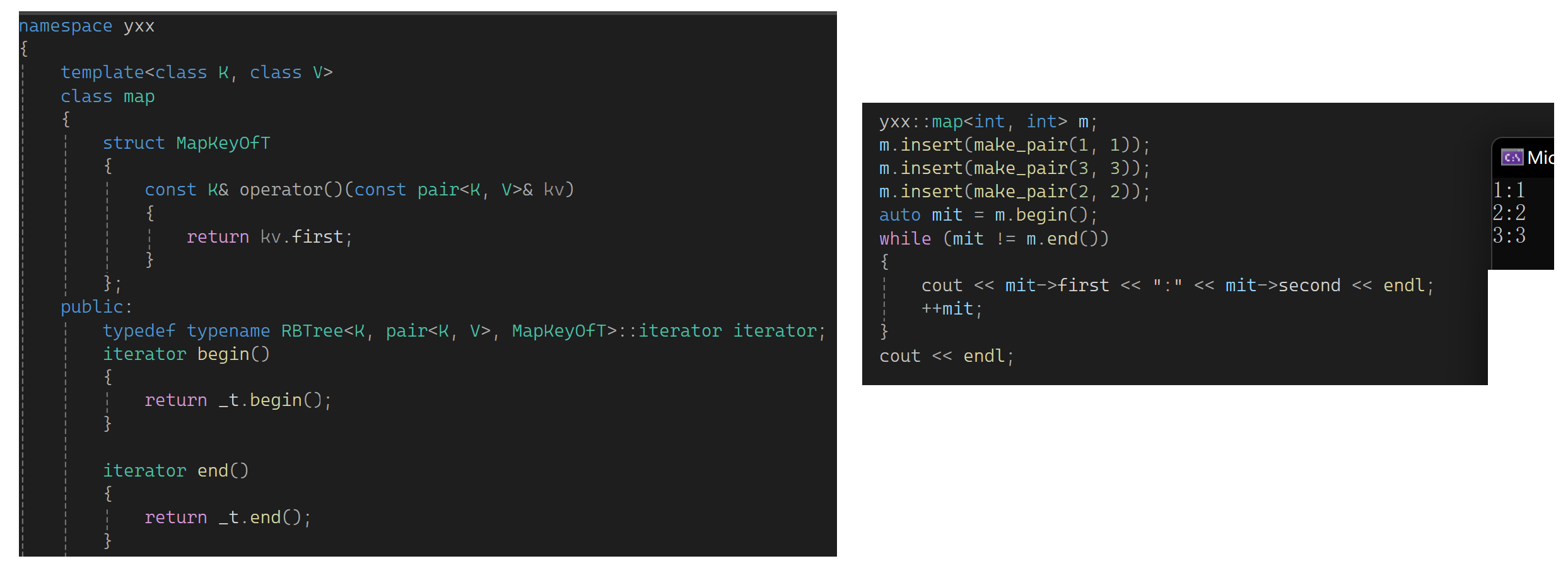
set容许修改吗?比如是偶数就+=10:
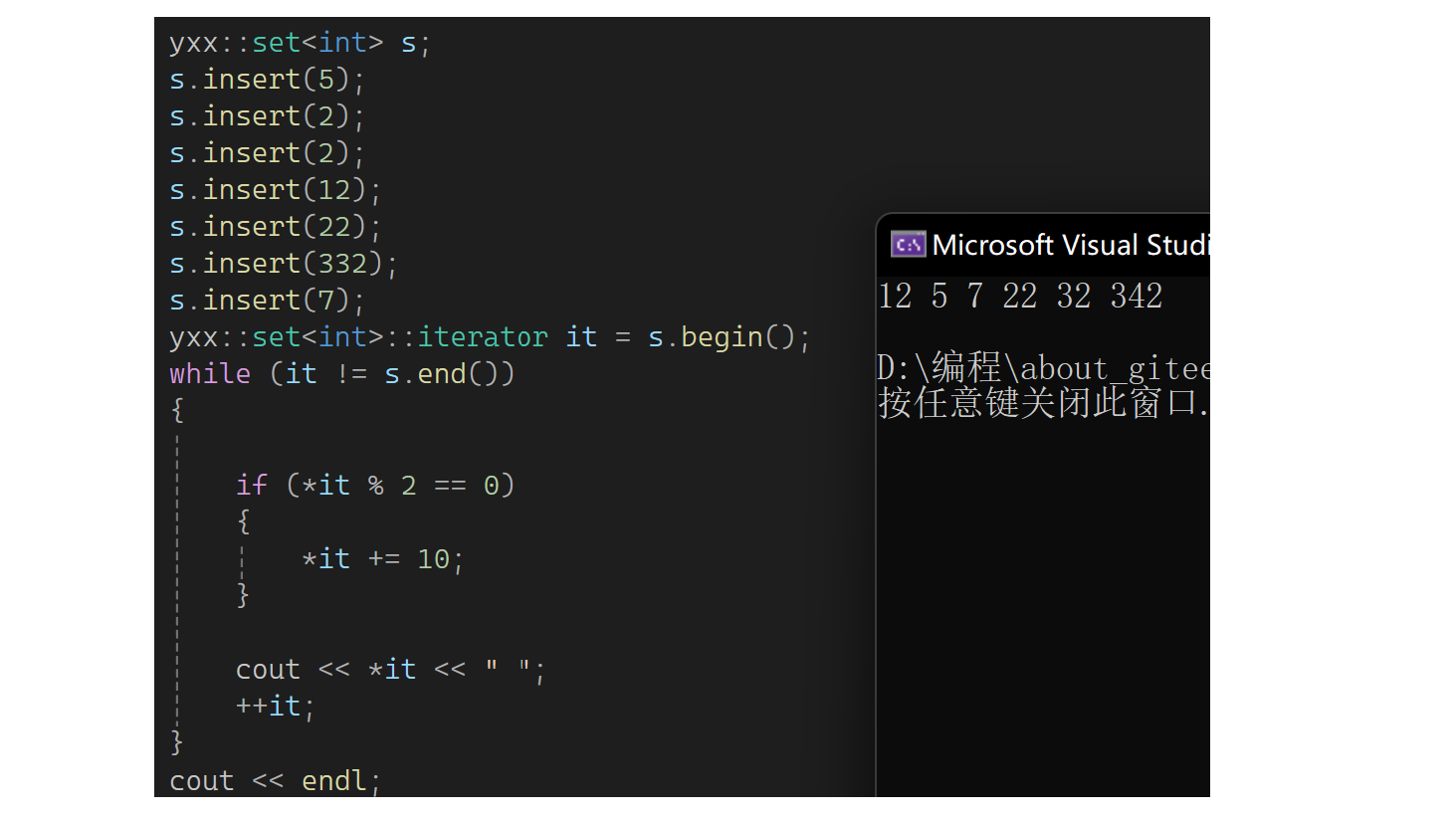
运行后发现不是搜索树了,因此不应该容许修改。看看set的库:

库里面const_iterator是const_iterator,iterator也是const_iterator。那map允许修改吗?允许修改value,不允许修改k。所以set的方案不能直接搞到map上,map这的迭代器是正常的:

map库里面在存储中解决了K不可改,V可改的问题:
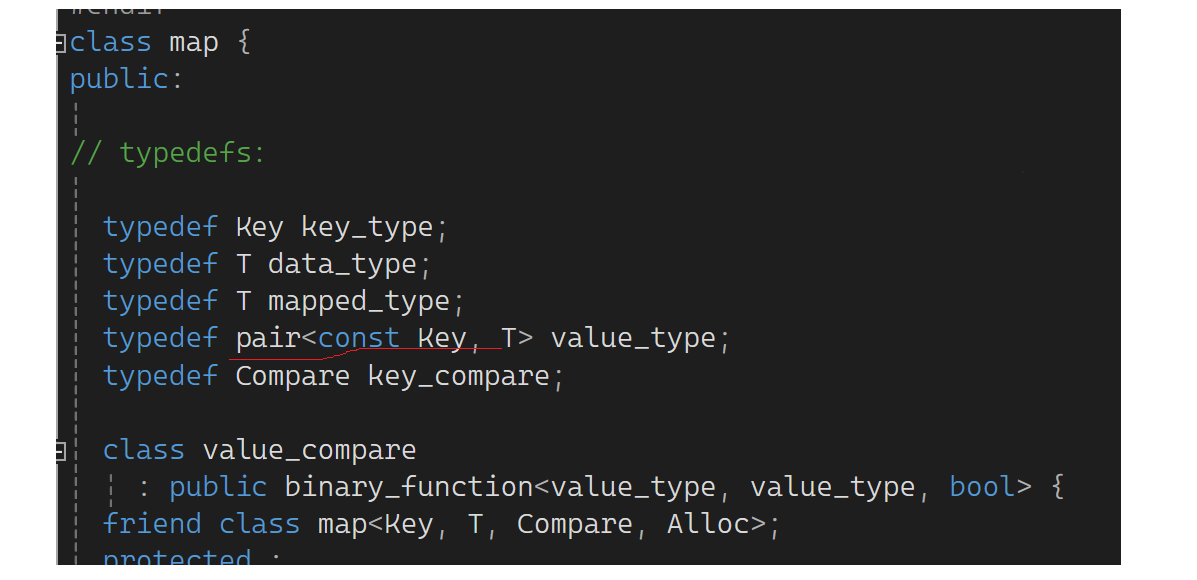
下面来完成const迭代器,只有把树的const迭代器弄好,才能去弄map和set。看下图:
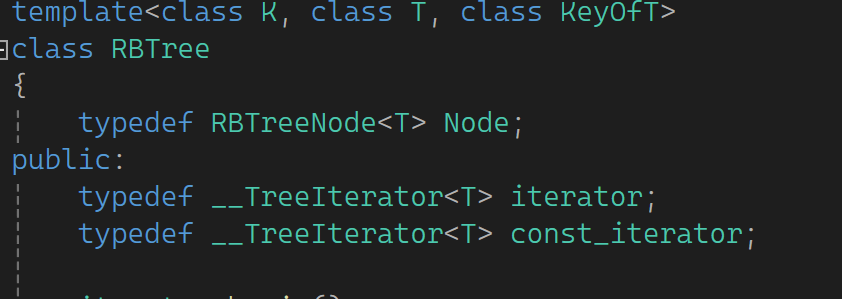
首先普通迭代器和const迭代器本身还是同一个类模板,只是用不同的模板参数进行相关的实例化:
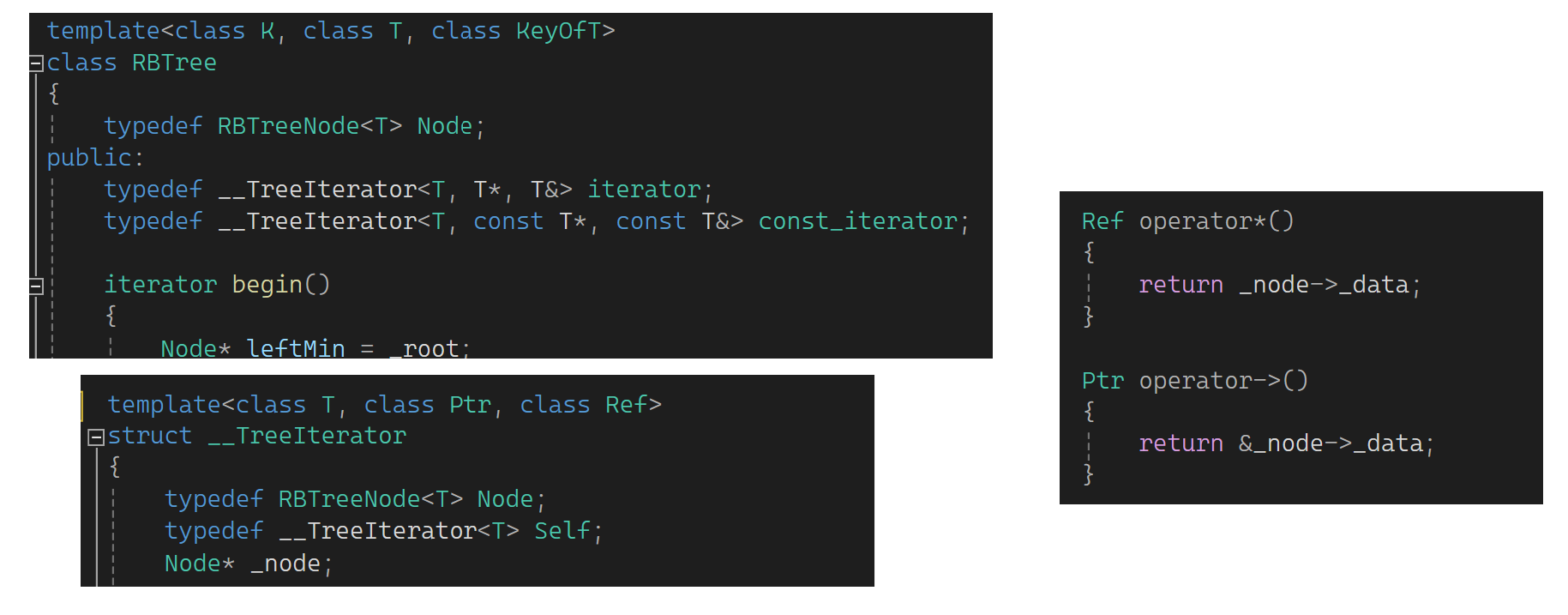
是看普通迭代器还是const迭代器就看这两个模板参数:
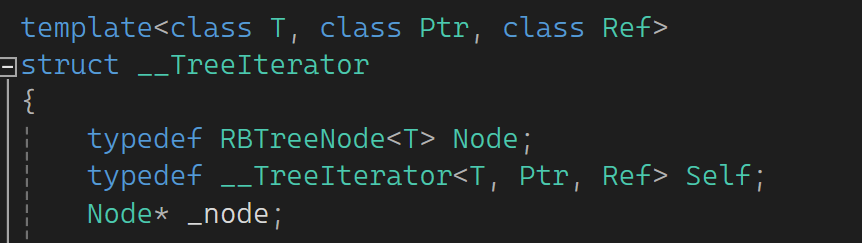
那Myset如何做const迭代器呢?

然后再提供一下const版本的:

现在再换一下set里面:
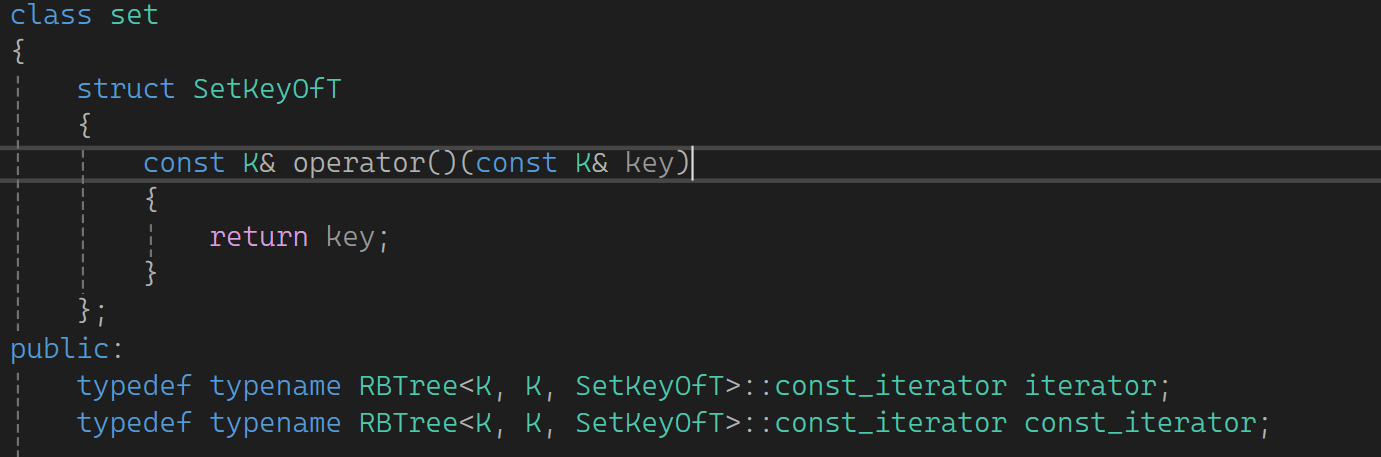
对于set来说普通迭代器和const迭代器都返回const迭代器,此时用前面例子再修改就不能修改了。因为*it去调用operator*,这里虽然是iterator it,但iterator底层用的是const_iterator,所以传的是const T*和const T&,调operator*时返回const T*就不能修改。看一下下图:
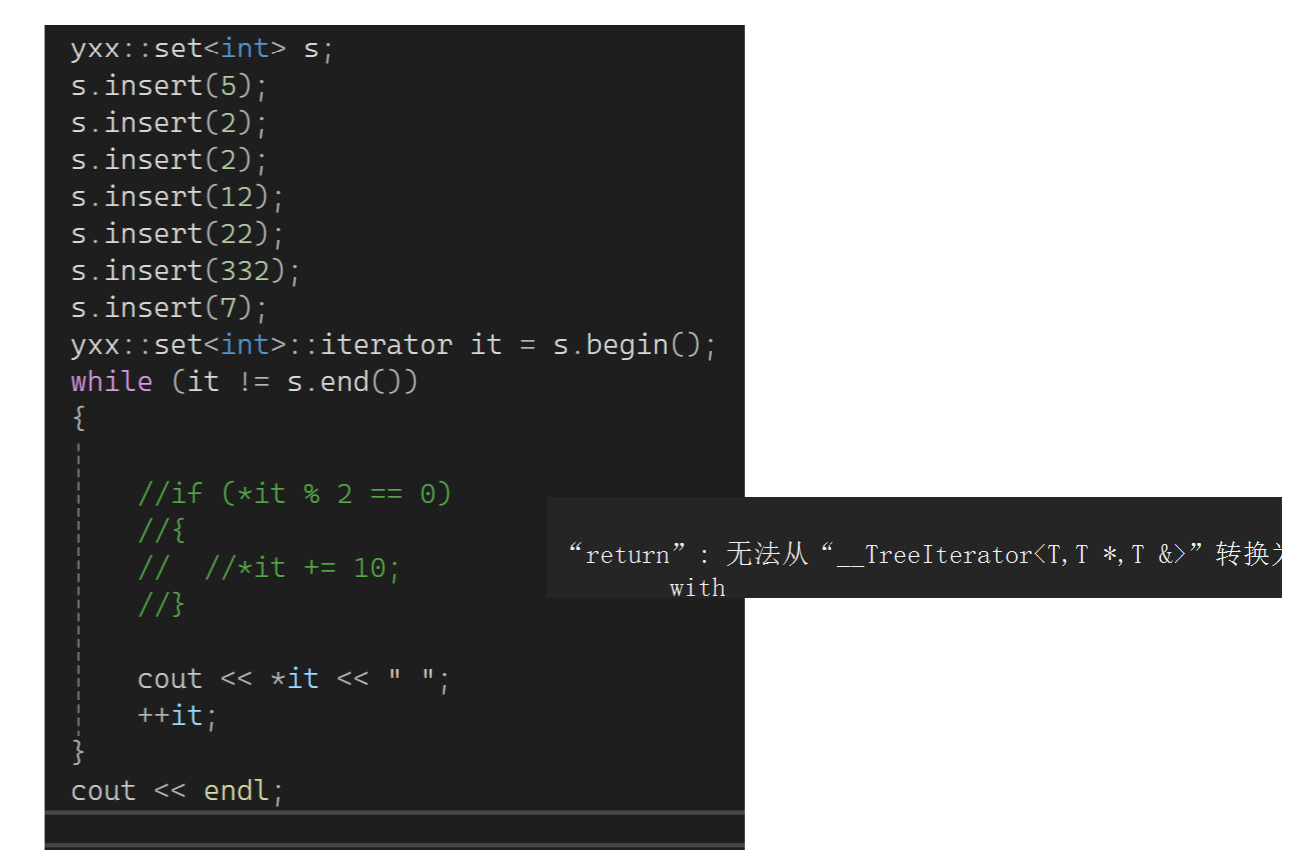
还是有报错,是因为:
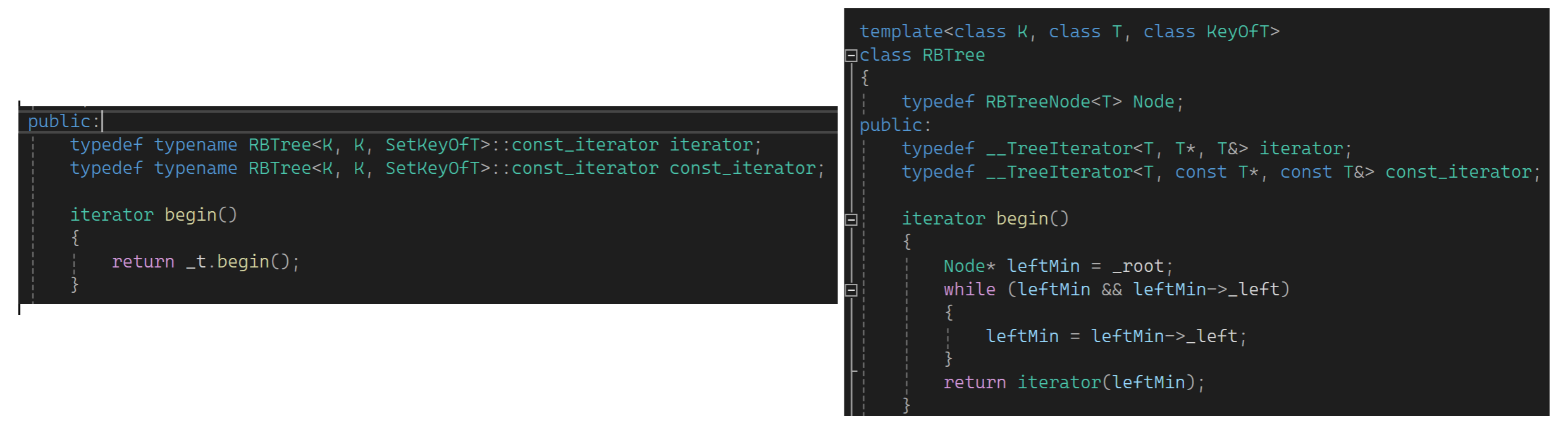
返回时存在转换,所以也要提供const版本:
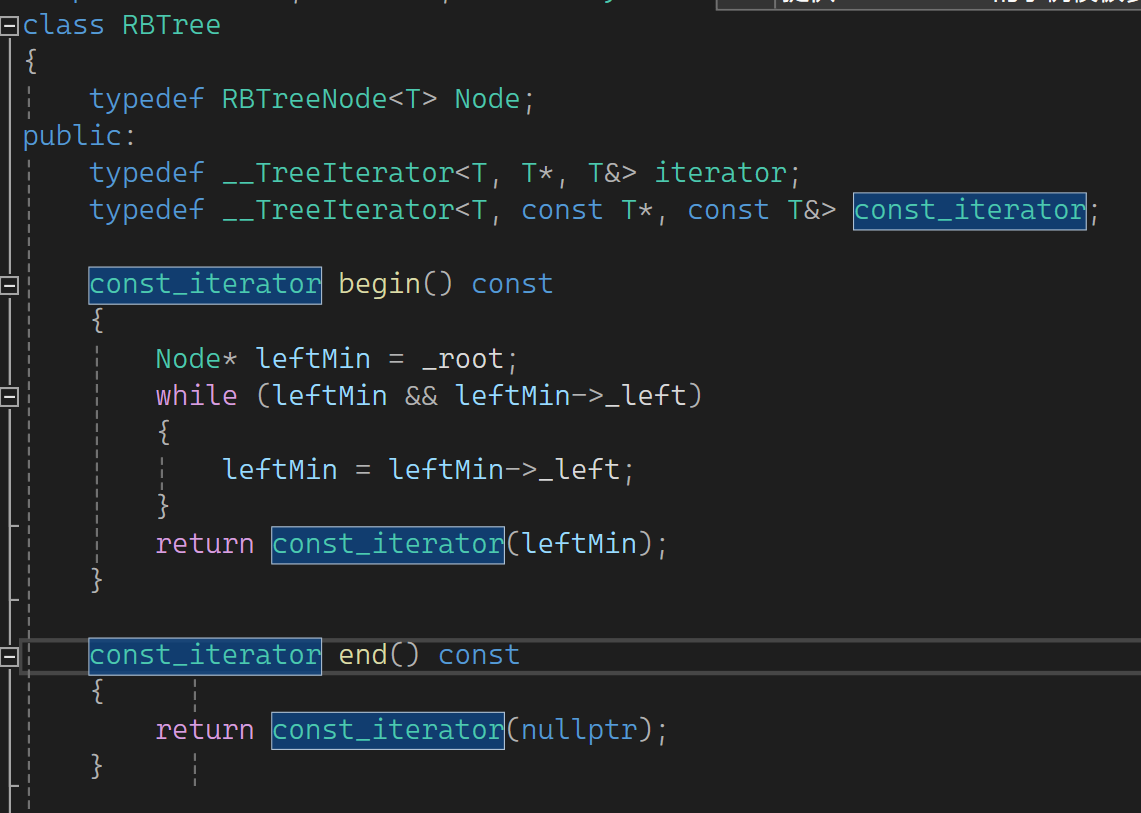
库里面是这样的,我们也学库里面的样子变变:

运行发现也可以,因为不加const,_t就是普的,普通的_t只能去调用begin,普通begin返回普通iterator,就不能匹配了。只提供const版本,反正不能修改,const对象可调用,普通对象也可以调用,这样set的const迭代器问题就解决了。
下面来解决一下map,要做到不能修改key,可以修改val:
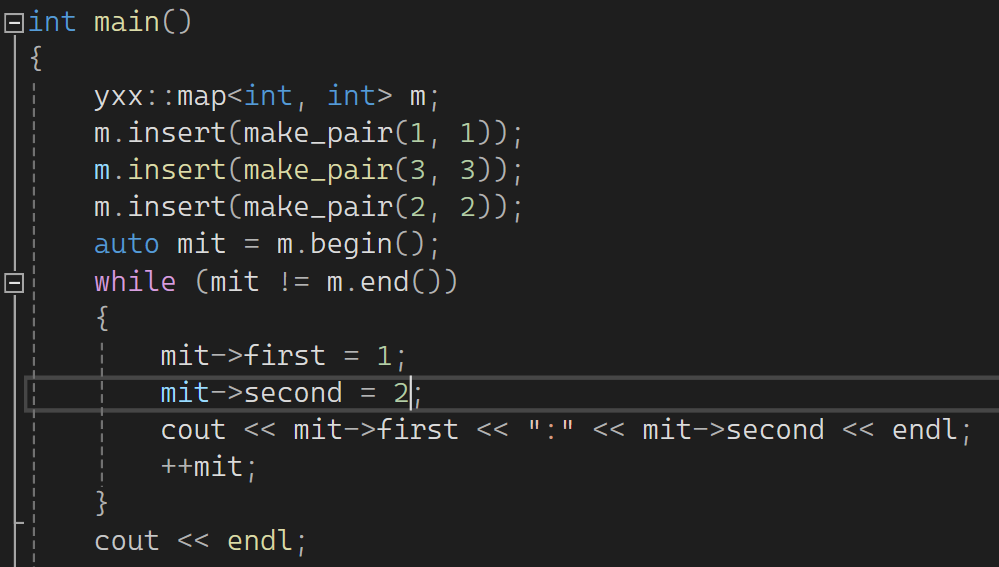
这里就不能用和set一样的方式了,假设也这样弄:
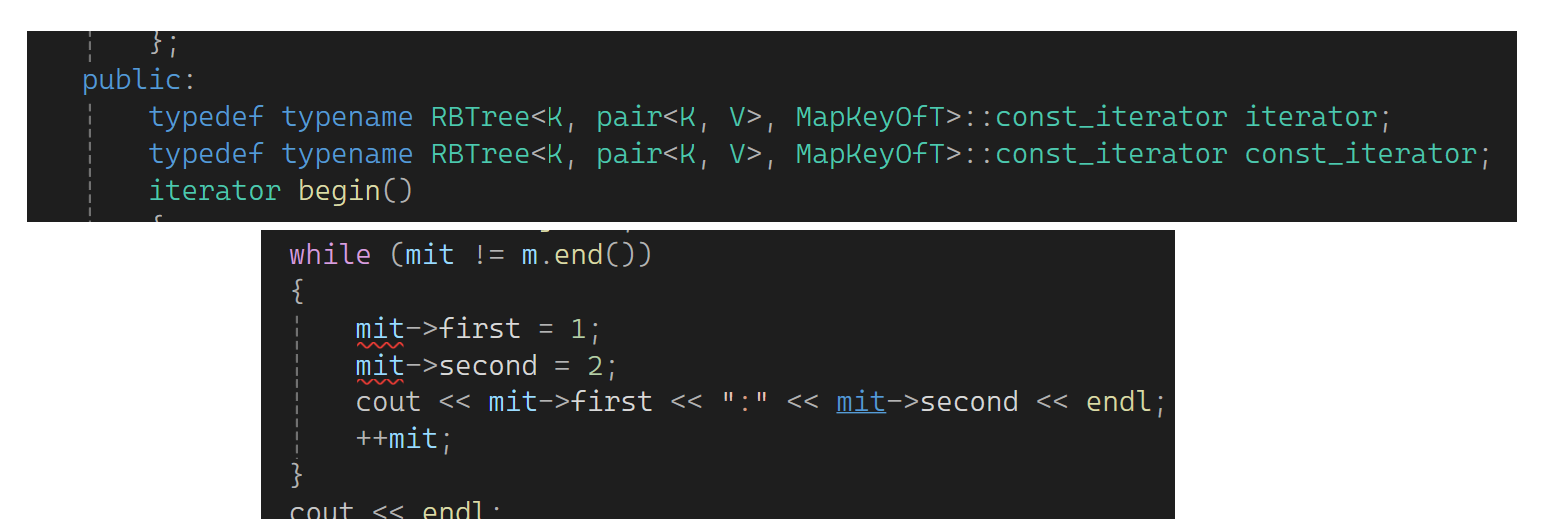
这样key和val都不能修改了。库中value_type的key是一个const key,所以这样变:
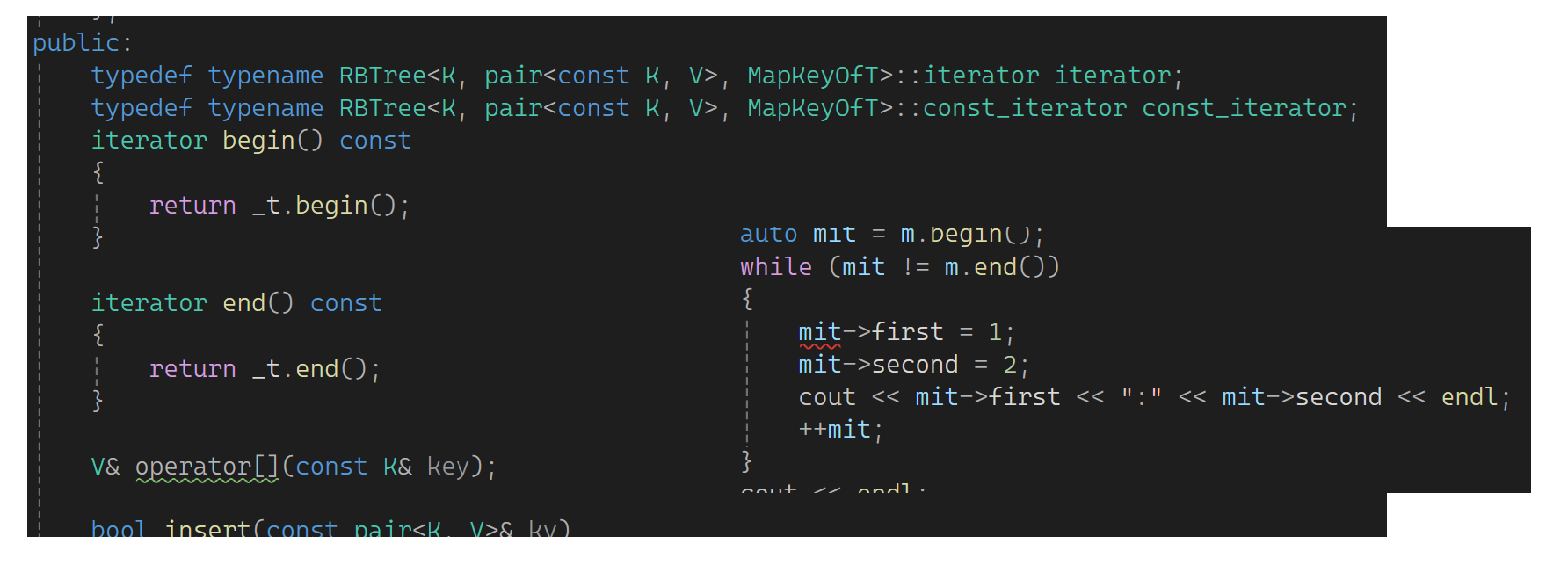
这样写pair没有被const修饰,pair的first被const修饰了。再修改一下错误:

它的const和普通的意义是普通迭代器可修改val不能修改key,const迭代器是key和val都不能改。
通过上述迭代器就差不多了,再补一下--:--怎么走呢?--就是++反向过来。如果_node左边不为空,下一个找整个左树最右边的结点。如果左树为空:
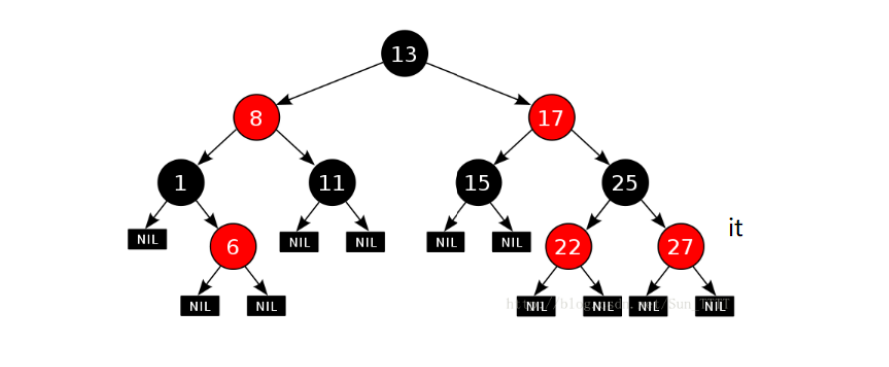
此时我是父亲的右,那么下一个访问父亲;我是父亲的左,就找孩子是父亲右的那一个:

--完成后迭代器就差不多了。库里的红黑树是这样的:
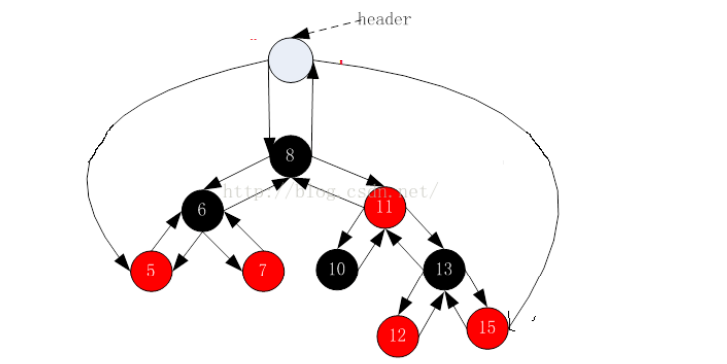
我们写的用空代表end,库里增加了一个哨兵位的头结点,它让哨兵位的左指针指向最小结点,让右指针指向最大结点,这样可以快速的找到最小和最大结点。因此它的begin和end是这样的:

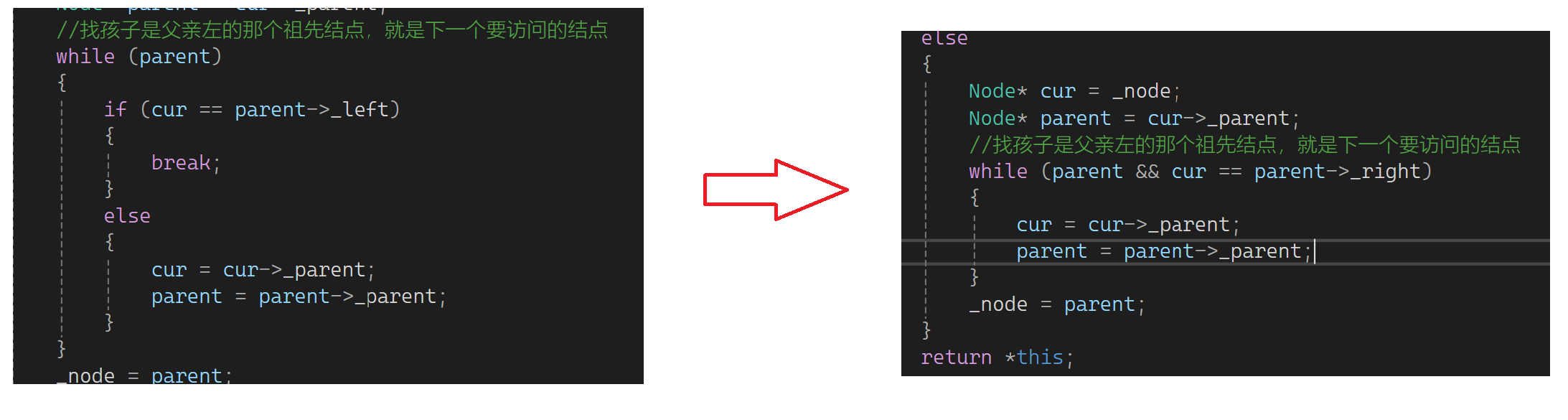
这里哨兵位让它的parent指向根,让root的parent指向哨兵位,意味着找根要root=header->parent。若有头结点++这里要改一下,要不然不太对,因为最后cur不是parent的左:
最后完善一下map中的operator[],要用insert去实现:

insert一个val后它的返回值是pair,pair的first是个iterator,second是个bool。需要把map中的insert改一下,先改RBTree中的:如果开始插入成功,返回新插入结点构建的迭代器:
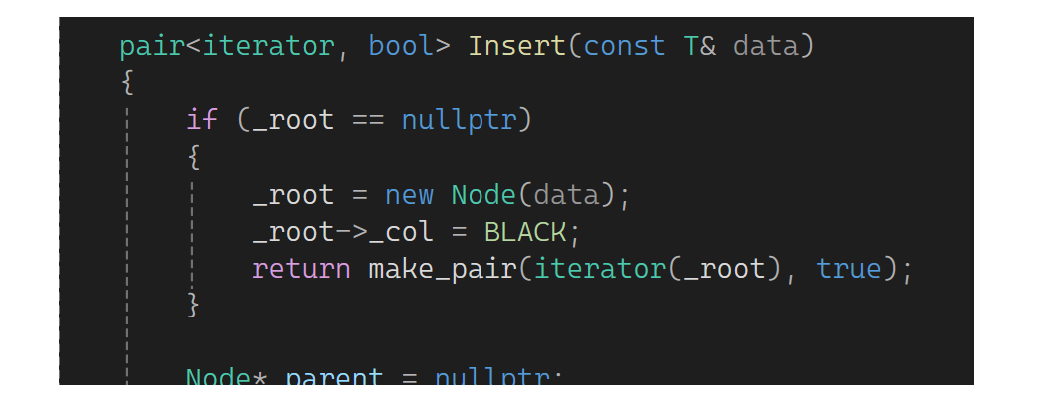
插入失败返回false,返回已有的结点构成的迭代器。最后插入成功,返回新插入结点构成的迭代器,新插入结点叫cur,但不能用,因为变色过程中可能会往上走,所以保存一下方便返回:
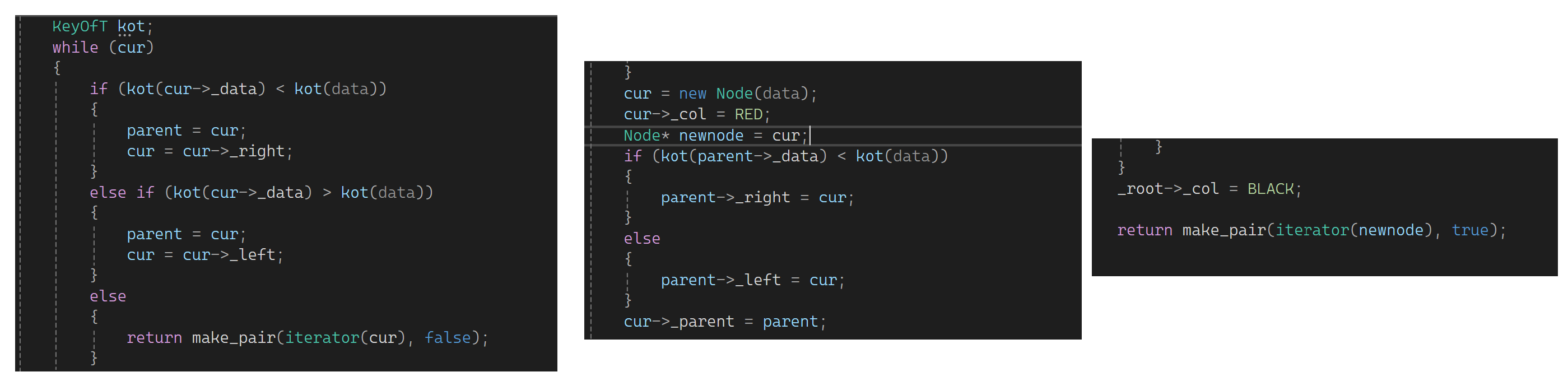
现在树里的insert改了,map和set也要跟着改:

但是有报错:

_t是普通对象,set调insert返回普通迭代器,pair这的iterator是树里的typedef过的const_iterator。库里是这样弄的:

它又去构造了一下,我们先抄过来:
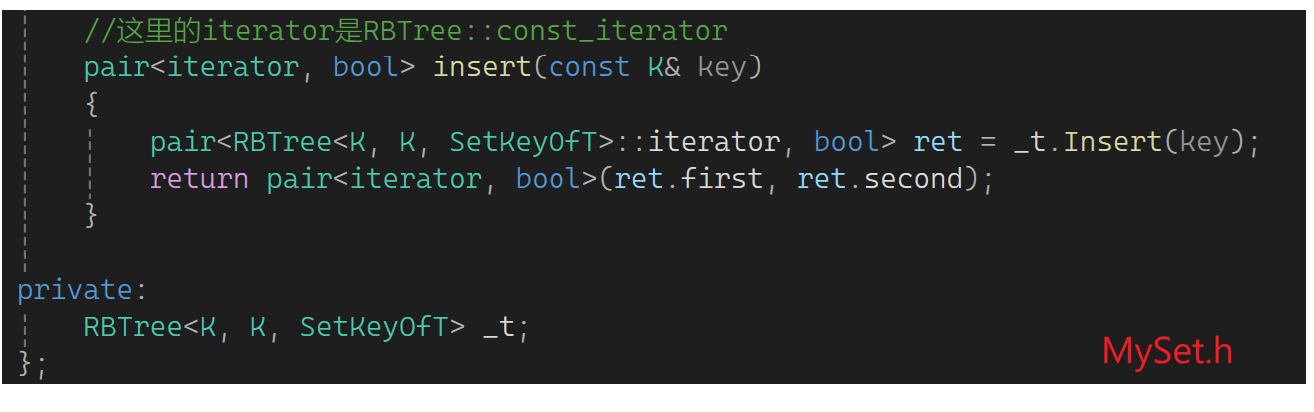
还是编不过,return这pair里的iterator是const的,ret.first返回的是普通的。pair的构造函数相当于有个iterator的x,bool的y,用x初始化first,y初始化second。x就是ret的first,是个普通迭代器,pair的first类型是const的iterator:

这里的本质是拿普通迭代器构造const迭代器。库里写了这样的函数:
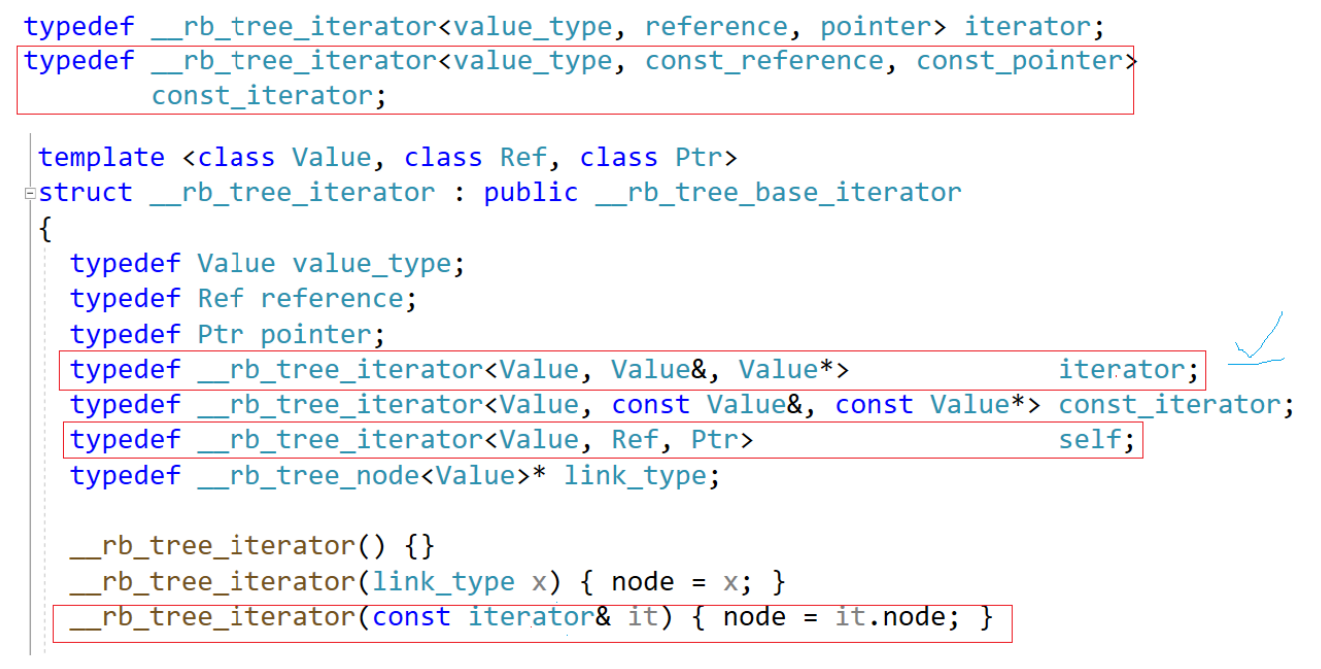
按理说迭代器不用写拷贝构造,编译器默认生成的拷贝就够了。但这里也不是纯拷贝构造,没有用self,仔细看self和iterator区别是什么?self一定是这个迭代器,iterator不一定是这个迭代器,那iterator是什么?再回顾一下:
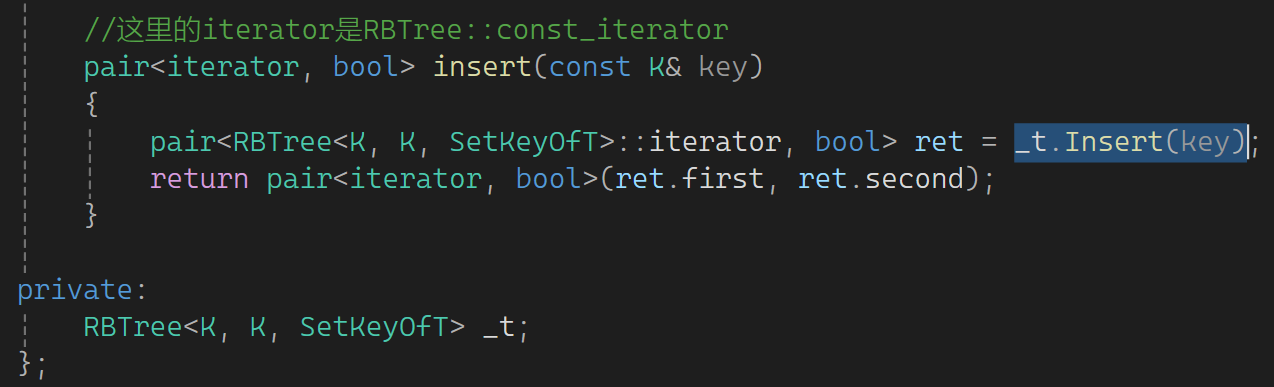
去调树的insert,树的insert的pair是普通迭代器,但set这一层为了解决key不能修改,它的普通迭代器和const迭代器都是树的const迭代器,这样就过不去。所以这单独用普通的树的迭代器接收,接收后再去构造,用普通迭代器构造const迭代器。普通迭代器为啥可去初始化const迭代器?因为const迭代器这支持了构造,这个类被实例化成const迭代器时,这个函数是一个构造,支持普通迭代器构造const迭代器。这个参数是iterator,它的特点是不管是普通还是const都是普通迭代器,因为这两个参数是values和values*,不受Ref和Ptr影响。当这个类被实例化普通迭代器,这个函数就是一个拷贝构造。现在需要的是普通迭代器去构造const迭代器,所以补充一下(它不用ptr):
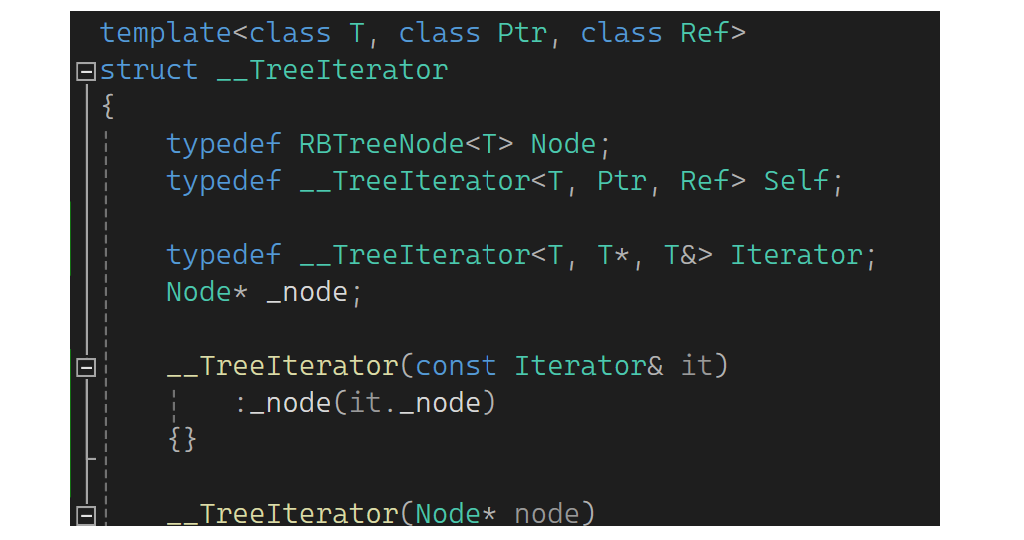
再补一下Map的[],这里先调inssert,里面插一个make_pair,first是k,values给个缺省值:

下面测试一下:
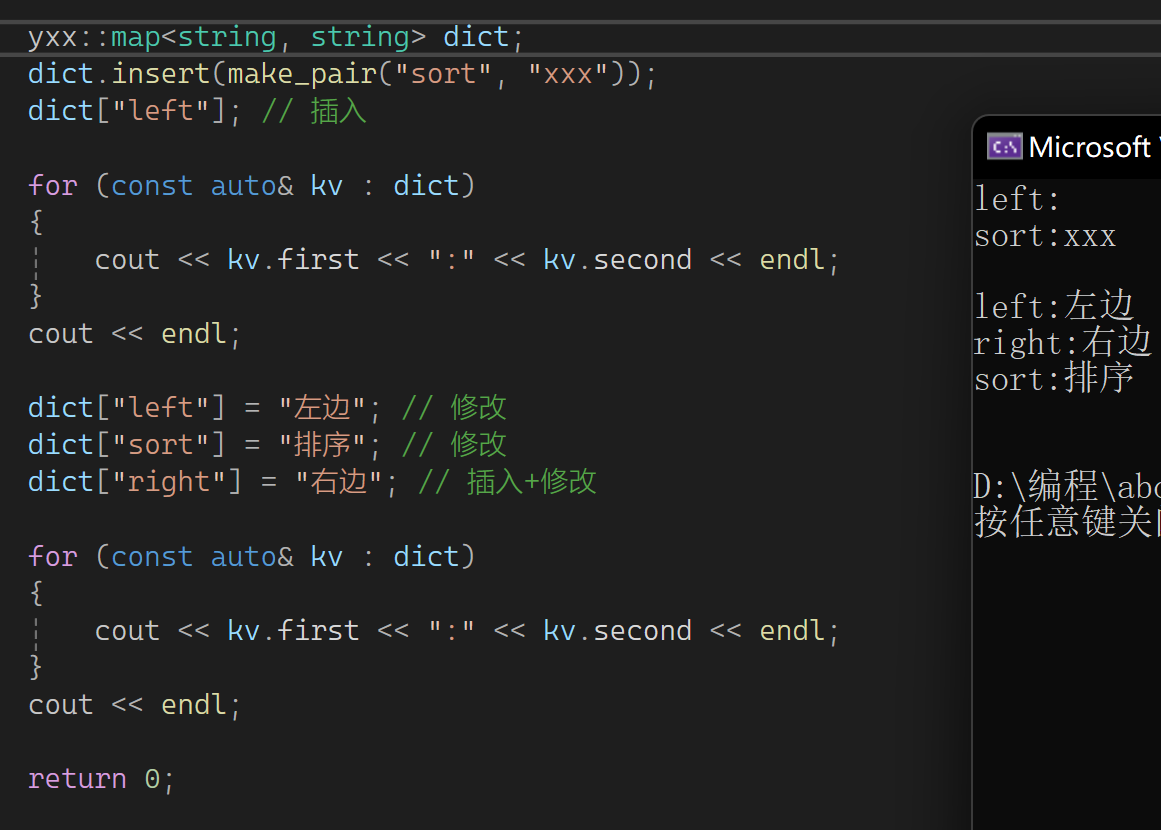
3.完整代码
//MySet.h
#pragma once
#include "RBTree.h"
namespace yxx
{
template<class K>
class set
{
struct SetKeyOfT
{
const K& operator()(const K& key)
{
return key;
}
};
public:
typedef typename RBTree<K, K, SetKeyOfT>::const_iterator iterator;
typedef typename RBTree<K, K, SetKeyOfT>::const_iterator const_iterator;
iterator begin() const
{
return _t.begin();
}
iterator end() const
{
return _t.end();
}
/*const_iterator begin() const
{
return _t.begin();
}
const_iterator end() const
{
return _t.end();
}*/
//这里的iterator是RBTree::const_iterator
pair<iterator, bool> insert(const K& key)
{
pair<RBTree<K, K, SetKeyOfT>::iterator, bool> ret = _t.Insert(key);
return pair<iterator, bool>(ret.first, ret.second);
}
private:
RBTree<K, K, SetKeyOfT> _t;
};
}
//Mymap.h
#pragma once
#include "RBTree.h"
namespace yxx
{
template<class K, class V>
class map
{
struct MapKeyOfT
{
const K& operator()(const pair<K, V>& kv)
{
return kv.first;
}
};
public:
typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::iterator iterator;
typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::const_iterator const_iterator;
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
const_iterator begin() const
{
return _t.begin();
}
const_iterator end() const
{
return _t.end();
}
V& operator[](const K& key)
{
pair<iterator, bool>ret = insert(make_pair(key, V()));
return ret.first->second;
}
pair<iterator, bool> insert(const pair<K, V>& kv)
{
return _t.Insert(kv);
}
private:
RBTree<K, pair<const K, V>, MapKeyOfT> _t;
};
}
//RBTree.h
#pragma once
#include <iostream>
using namespace std;
enum Colour
{
RED,
BLACK
};
template<class T>
struct RBTreeNode
{
RBTreeNode<T>* _left;
RBTreeNode<T>* _right;
RBTreeNode<T>* _parent;
T _data;
Colour _col;
RBTreeNode(const T& data)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_data(data)
,_col(RED)
{}
};
template<class T, class Ptr, class Ref>
struct __TreeIterator
{
typedef RBTreeNode<T> Node;
typedef __TreeIterator<T, Ptr, Ref> Self;
typedef __TreeIterator<T, T*, T&> Iterator;
Node* _node;
__TreeIterator(const Iterator& it)
:_node(it._node)
{}
__TreeIterator(Node* node)
:_node(node)
{}
Ref operator*()
{
return _node->_data;
}
Ptr operator->()
{
return &_node->_data;
}
bool operator!=(const Self& s)
{
return _node != s._node;
}
bool operator==(const Self& s)
{
return _node == s._node;
}
Self& operator--()
{
if (_node->_left)
{
//左树的最右结点
Node* subRight = _node->_left;
while (subRight->_right)
{
subRight = subRight->_right;
}
_node = subRight;
}
else
{
//孩子是父亲右的那个结点
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && cur == parent->_left)
{
cur = cur->_parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
Self& operator++()
{
if (_node->_right)
{
//右树的最左结点
Node* subLeft = _node->_right;
while (subLeft->_left)
{
subLeft = subLeft->_left;
}
_node = subLeft;
}
else
{
Node* cur = _node;
Node* parent = cur->_parent;
//找孩子是父亲左的那个祖先结点,就是下一个要访问的结点
while (parent && cur == parent->_right)
{
cur = cur->_parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
};
template<class K, class T, class KeyOfT>
class RBTree
{
typedef RBTreeNode<T> Node;
public:
typedef __TreeIterator<T, T*, T&> iterator;
typedef __TreeIterator<T, const T*, const T&> const_iterator;
iterator begin()
{
Node* leftMin = _root;
while (leftMin && leftMin->_left)
{
leftMin = leftMin->_left;
}
return iterator(leftMin);
}
iterator end()
{
return iterator(nullptr);
}
const_iterator begin() const
{
Node* leftMin = _root;
while (leftMin && leftMin->_left)
{
leftMin = leftMin->_left;
}
return const_iterator(leftMin);
}
const_iterator end() const
{
return const_iterator(nullptr);
}
Node* Find(const K& key)
{
Node* cur = _root;
KeyOfT kot;
while (cur)
{
if (kot(cur->_data) < key)
{
cur = cur->_right;
}
else if(kot(cur->_data) > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
pair<iterator, bool> Insert(const T& data)
{
if (_root == nullptr)
{
_root = new Node(data);
_root->_col = BLACK;
return make_pair(iterator(_root), true);
}
Node* parent = nullptr;
Node* cur = _root;
KeyOfT kot;
while (cur)
{
if (kot(cur->_data) < kot(data))
{
parent = cur;
cur = cur->_right;
}
else if (kot(cur->_data) > kot(data))
{
parent = cur;
cur = cur->_left;
}
else
{
return make_pair(iterator(cur), false);
}
}
cur = new Node(data);
cur->_col = RED;
Node* newnode = cur;
if (kot(parent->_data) < kot(data))
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
while (parent && parent->_col == RED)
{
Node* grandfather = parent->_parent;
if (parent == grandfather->_left)
{
Node* uncle = grandfather->_right;
if (uncle && uncle->_col == RED)
{
//变色
parent->_col = uncle->_col = BLACK;
cur->_col = RED;
//继续向上处理
cur = grandfather;
parent = cur->_parent;
}
else //u不存在 或 存在且为黑
{
if (cur == parent->_left)
{
RotateR(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else
{
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
else //parent == grandfather->right
{
Node* uncle = grandfather->_left;
//u存在且为红
if (uncle && uncle->_col == RED)
{
//变色
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
//继续向上处理
cur = grandfather;
parent = cur->_parent;
}
else
{
if (cur == parent->_right)
{
//g
// p
// c
RotateL(grandfather);
grandfather->_col = RED;
parent->_col = BLACK;
}
else
{
// g
// p
// c
RotateR(parent);
RotateL(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
}
_root->_col = BLACK;
return make_pair(iterator(newnode), true);
}
void RotateL(Node* parent)
{
Node* cur = parent->_right;
Node* curleft = cur->_left;
parent->_right = curleft;
if (curleft)
{
curleft->_parent = parent;
}
cur->_left = parent;
Node* ppnode = parent->_parent;
parent->_parent = cur;
if (parent == _root)
{
_root = cur;
cur->_parent = nullptr;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = cur;
}
else
{
ppnode->_right = cur;
}
cur->_parent = ppnode;
}
}
void RotateR(Node* parent)
{
Node* cur = parent->_left;
Node* curright = cur->_right;
parent->_left = curright;
if (curright)
curright->_parent = parent;
Node* ppnode = parent->_parent;
cur->_right = parent;
parent->_parent = cur;
if (ppnode == nullptr)
{
_root = cur;
cur->_parent = nullptr;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = cur;
}
else
{
ppnode->_right = cur;
}
cur->_parent = ppnode;
}
}
bool CheckColour(Node* root, int blacknum, int benchmark)
{
if (root == nullptr)
{
if (blacknum != benchmark)
return false;
return true;
}
if (root->_col == BLACK)
{
++blacknum;
}
if (root->_col == RED && root->_parent && root->_parent->_col == RED)
{
cout << root->_kv.first << "连续";
return false;
}
return CheckColour(root->_left, blacknum, benchmark)
&& CheckColour(root->_right, blacknum, benchmark);
}
bool IsBalance()
{
return IsBalance(_root);
}
bool IsBalance(Node* root)
{
if (root == nullptr)
return true;
if (root->_col != BLACK)
{
return false;
}
//基准值
int benchmark = 0;
Node* cur = root;
while (cur)
{
if (cur->_col == BLACK)
benchmark++;
cur = cur->_left;
}
return CheckColour(root, 0, benchmark);
}
private:
Node* _root = nullptr;
};
//Test.cpp
#define _CRT_SECURE_NO_WARNINGS 1
#include "MyMap.h"
#include "MySet.h"
int main()
{
//yxx::map<int, int> m;
//m.insert(make_pair(1, 1));
//m.insert(make_pair(3, 3));
//m.insert(make_pair(2, 2));
//auto mit = m.begin();
//while (mit != m.end())
//{
// //mit->first = 1;
// mit->second = 2;
// cout << mit->first << ":" << mit->second << endl;
// ++mit;
//}
//cout << endl;
///*
//yxx::set<int> s;
//s.insert(5);
//s.insert(2);
//s.insert(7);
//yxx::set<int>::iterator it = s.begin();
//while (it != s.end())
//{
// cout << *it << endl;
// ++it;
//}
//cout << endl;*/
//yxx::set<int> s;
//s.insert(5);
//s.insert(2);
//s.insert(2);
//s.insert(12);
//s.insert(22);
//s.insert(332);
//s.insert(7);
//yxx::set<int>::iterator it = s.begin();
//while (it != s.end())
//{
//
///* if (*it % 2 == 0)
// {
// (*it) += 10;
// }*/
// cout << *it << " ";
// ++it;
//}
//cout << endl;
yxx::map<string, string> dict;
dict.insert(make_pair("sort", "xxx"));
dict["left"]; // 插入
for (const auto& kv : dict)
{
cout << kv.first << ":" << kv.second << endl;
}
cout << endl;
dict["left"] = "左边"; // 修改
dict["sort"] = "排序"; // 修改
dict["right"] = "右边"; // 插入+修改
for (const auto& kv : dict)
{
cout << kv.first << ":" << kv.second << endl;
}
cout << endl;
return 0;
}