一、树的定义与基本概念
树是n(n ≥0))个结点的有限集合:
当n=0 时,称为空树;
当n>0时,满足:
1.有且仅有一个根结点(Root);
2.其余结点可分为 m(m ≥0)个互不相交的有限集合T1,T2,...,Tm,每个集合本身也是一棵树,称为根的子树(Subtree)
树是一种非线性数据结构,由节点(Node)和边(Edge)组成,具有以下特性:
- 根节点(Root):树的顶层节点,没有父节点。
- 子节点(Child):一个节点通过边连接的下一层节点。
- 父节点(Parent):子节点的直接上层节点。
- 叶字(终端节点):度为0的节点。
- 节点的度: 子树的个数。
- 树的度:所有节点最大的节点度。
- 非终端及节点(分支节点):度不为0.
- 深度(Depth):从根节点到当前节点的边数。
- 高度(Height):从当前节点到最远叶节点的边数
二、树的常见类型
二叉树:由一个根节点和两个互不相交的子树组成。每个节点最多有两个子节点(左子节点和右子节点)。
特点:
1.每个结点最多有两个子树;
2.左、右子树有顺序,不可互换;
3.即使某结点仅有一个子树,也必须明确是左子树还是右子树。
- 满二叉树:所有非叶节点均有左右子节点,且所有叶节点在同一层。
- 完全二叉树 :除最后一层外,其他层节点数达到最大值,最后一层从左向右填充。
从这里我们也可以得出一些完全二叉树的特点:
(1)叶子结点只能出现在最下两层。
(2)最下层的叶子一定集中在左部连续位置。
(3)倒数两层,若有叶子结点,一定都在右部连续位置。
(4)如果结点度为1,则该结点只有左孩子,即不存在只有右子树的情况。
(5)同样结点数的二叉树,完全二叉树的深度最小。
重要性质:
-
1.第i层(i≥1)上最多有2
^(i-1)个结点;
-
2.深度为k的二叉树最多有2^k-1个结点;
-
3.对任意非空二叉树,:设:no:叶子结点数(度为0)n2:度为2的结点数则恒有:no=n2+14.具有n个结点的完全二叉树,其深度为:[log2n」+1(向下取整)
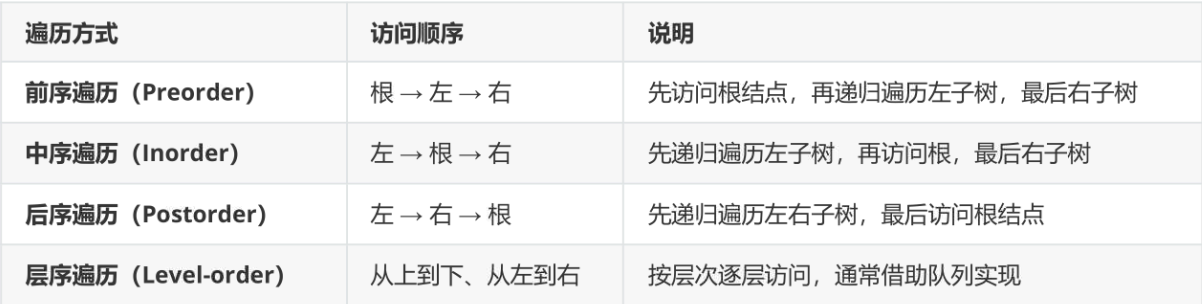
三、树的遍历方式
深度优先遍历(DFS):
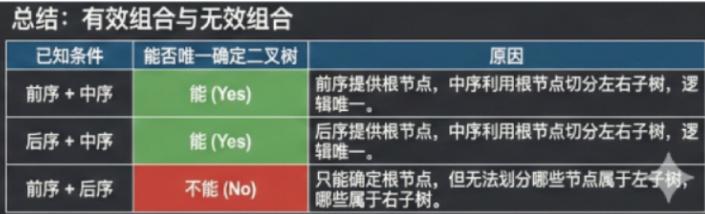
- 前序遍历:根节点 → 左子树 → 右子树。
- 中序遍历:左子树 → 根节点 → 右子树(二叉搜索树中结果为有序序列)。
- 后序遍历:左子树 → 右子树 → 根节点。
广度优先遍历(BFS) :按层级遍历,使用队列实现。
四、树的算法
cs
typedef char data_t;
typedef struct btree
{
data_t data;
struct btree *pl;
struct btree *pr;
}btree_t;
//前序遍历的扩展序列
char tree_seq[] = "ABDG##H###CE#I##F##";
int idx = 0;
btree_t *create_btree(void)
{
char data = tree_seq[idx];
idx++;
if(data == '#')
{
return NULL;//NULL 表示结束
}
btree_t *new = malloc(sizeof(btree_t));
if(new == NULL)
{
printf("%s:malloc fail\n",__func__);
return NULL;
}
new->data = data;//根
new->pl = create_btree();//左
new->pr = create_btree();//右
return new;
}//最终返回根节点
int pre_order_traverse(btree_t *t)
{
if(t == NULL)
{
return 0;
}
printf("%c ",t->data);
pre_order_traverse(t->pl);
pre_order_traverse(t->pr);
return 0;
}
int in_order_traverse(btree_t *t)
{
if(t != NULL)
{
in_order_traverse(t->pl);
printf("%c ",t->data);
in_order_traverse(t->pr);
}
return 0;
}
int post_order_traverse(btree_t *t)
{
if(t != NULL)
{
post_order_traverse(t->pl);
post_order_traverse(t->pr);
printf("%c ",t->data);
}
return 0;
}
五、存储数据
数组线性表:0 (n)
链表:0(n)
树:---logN
哈希存储基本的思想:将数据的关键字 和 存储位置 之间 建立一种映射关系;
哈希冲突不可避免;
处理哈希冲突:1.开放地址法;2.链(链式)地址法
s1.p_new->next = hash_table[4];
s2.hash_table[4] = p_new;
数组typedef struct node
{
data_t data;
struct node * next;
}node_t;
node_t * hash_table[10];//哈希表---初始化为 NULL(全局变量)
int hash_insert (data_t data)
{
取余法算出下标
/ /b.进行插入
sl.p_new->next = hash_table[4] ;
s2. hash_table[4] = p_new;
}
cs
typedef int data_t;
typedef struct node
{
data_t data;
struct node *next;
}node_t;
#define size 10
node_t *hash_table[size] = {NULL};
int hash_insert(data_t data)
{
int k = data % size;
node_t *p_new = malloc(sizeof(node_t));
if(p_new == NULL)
{
printf("malloc fail%s\n",__func__);
return -1;
}
p_new->data = data;
p_new->next = hash_table[k];
hash_table[k] = p_new;
return 0;
}
int hash_show()
{
for(int j = 0;j < size;j++)
{
printf("%d|->",j);
if(hash_table[j] != NULL)
{
while(hash_table[j] != NULL)
{
printf("%d-> ",hash_table[j]->data);
hash_table[j] = hash_table[j]->next;
}
printf("NULL");
}
putchar('\n');
}
return 0;
}
int main()
{
int a[]={18,23,45,62,71,85,94,34};
int len = sizeof(a)/sizeof(a[0]);
for(int i = 0;i < len;i++)
{
hash_insert(a[i]);
}
hash_show();
// printf("data = %d\n",hash_table[34%size]->data);
return 0;
}